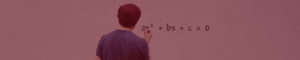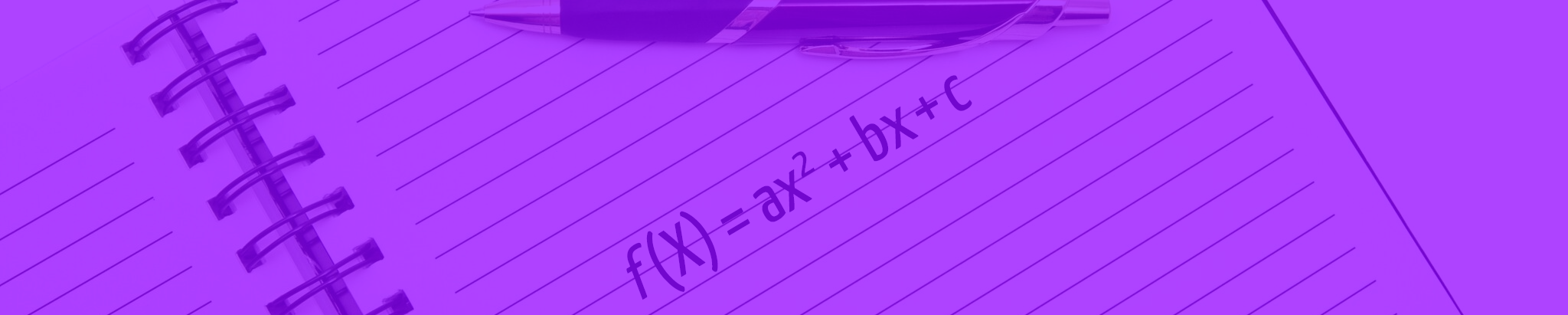O método da soma e produto é um método prático utilizado para determinar as raízes das equações do 2º grau. Ele é conhecido desta forma, porque faz uso de duas importantes relações de soma e produto entre as raízes e os coeficientes a, b e c da equação do segundo grau.

 

Olá, pessoal! Tudo certo por aí?

No texto de hoje, nós vamos fugir um pouco da fórmula de Bhaskara e resolver as equações do 2º grau através de um método que utiliza duas operações básicas da matemática. O método da soma e produto pode facilitar e agilizar muito a obtenção das raízes de uma equação do 2º grau, principalmente quando estas são números inteiros. De quebra, ele ainda nos ajuda a desenvolver o raciocínio!

Legal, não é mesmo? Então, chega de perder tempo! Vamos aprender de uma vez por todas a resolver as equações do segundo grau através do método da soma e produto. Vem comigo!

 

1. SOMA E PRODUTO

A equação do 2º grau “ax² + bx + c = 0” possui duas importantes relações entre as suas raízes x₁ e x₂ e os seus coeficientes a, b e c. Essas relações são conhecidas como Soma e Produto ou, também, como Relações de Girard.

Reparem na imagem acima, que de acordo com as Relações de Girard, a soma das duas raízes x₁ e x₂ de qualquer equação do 2º grau, resulta sempre no valor oposto ou contrário ao quociente entre os coeficientes b e a da equação. Além disso, o produto das mesmas raízes x₁ e x₂ resulta no valor do quociente entre os coeficientes c e a da equação.

Dúvidas sobre as raízes e os coeficientes da equação do 2º grau? Então, clique aqui.

Pensando nestas duas relações (literalmente!) é possível descobrir o valor numérico das duas raízes da equação do 2º grau de forma simples e prática. Vamos entender no próximo item como e quando devemos usar o método da soma e produto. Acompanhem!

 

2. COMO UTILIZAR O MÉTODO DA SOMA E PRODUTO?

Para encontrar as duas raízes de uma equação do segundo grau através do método da soma e produto, vocês precisam pensar em dois números que somados resultam no valor numérico oposto ao quociente entre os coeficientes b e a e que multiplicados resultam no valor numérico equivalente ao quociente entre os coeficientes c e a da equação.

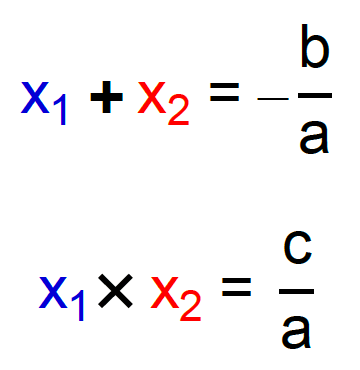
É claro que por envolver o nosso raciocínio e não entregar os resultados de uma forma direta como acontece na fórmula de Bhaskara, por exemplo, esse método pode não ser tão simples no início de nossa jornada rumo ao conhecimento. Assim, para facilitar a utilização do método, vocês podem seguir os passos descritos abaixo.

 

1º Passo: obtenha os valores numéricos equivalentes aos quocientes –b/a e c/a e monte as relações de soma e produto.

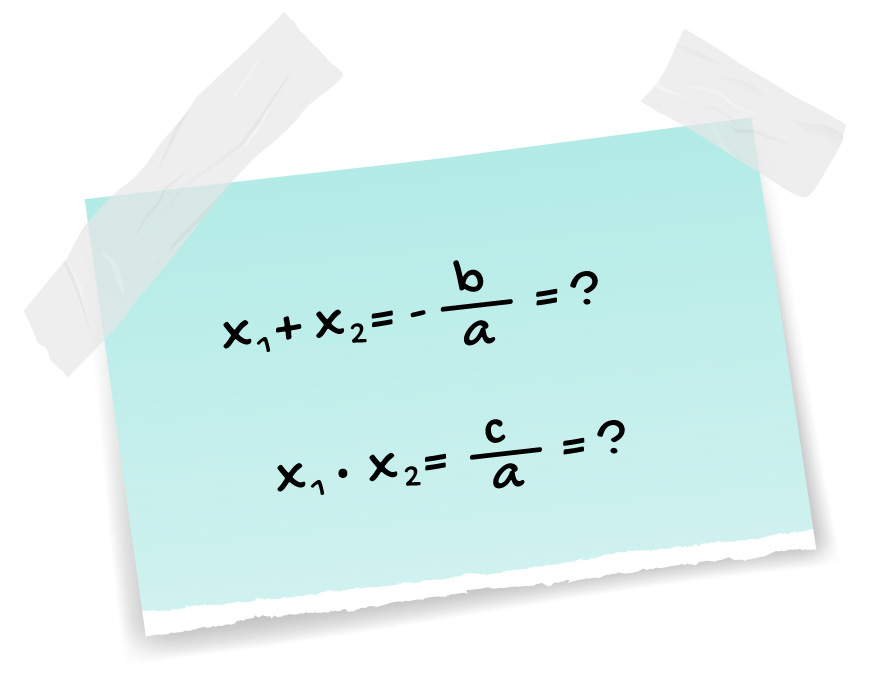
Dada a equação x² – 10x + 21 = 0, sabemos que a = 1, b = – 10 e c = 21. Portanto, o quociente – b/a é igual a 10 e o quociente c/a é igual a 21. Assim, chegamos as seguintes relações:

x₁ + x₂ = 10

x₁ ∙ x₂ = 21.

 

2º Passo: analise a relação de produto entre as raízes e determine algumas possibilidades que resultam no valor de c/a.

x₁ ∙ x₂ = 21

Segundo a relação acima, precisamos encontrar dois números cujo produto gera como resultado o valor 21. As possibilidades nesse caso se resumem as seguintes:

1 x 21 ou 21 x 1= 21

3 x 7 ou 7 x 3 = 21.

Uma dica importante nesse passo é reparar no sinal dos resultados obtidos nas relações de soma e produto. Neste exemplo, 10 e 21 são dois valores positivos. De acordo com as regras dos sinais para a adição e para a multiplicação, isso só pode significar que ambas as raízes da equação serão positivas também. Caso algum dos resultados fosse negativo, saberíamos que uma ou as duas raízes poderiam ser negativas, e assim, o número de possibilidades poderia aumentar.

 

3º Passo: teste as possibilidades encontradas na relação de soma entre as raízes e verifique se alguma delas resulta no valor de –b/a.

1 + 21 = 22 

3 + 7 = 10 

E não é que uma das possibilidades que encontramos para o produto também funciona para a relação de soma entre as duas raízes? Isso nos permite concluir que as raízes x₁ e x₂ da equação x² – 10x + 21 = 0 são iguais a 3 e 7.

3 + 7 = 10

3 ∙ 7 = 21

S = {3, 7}

 

3. QUANDO O MÉTODO DA SOMA E PRODUTO NÃO É O MAIS APROPRIADO

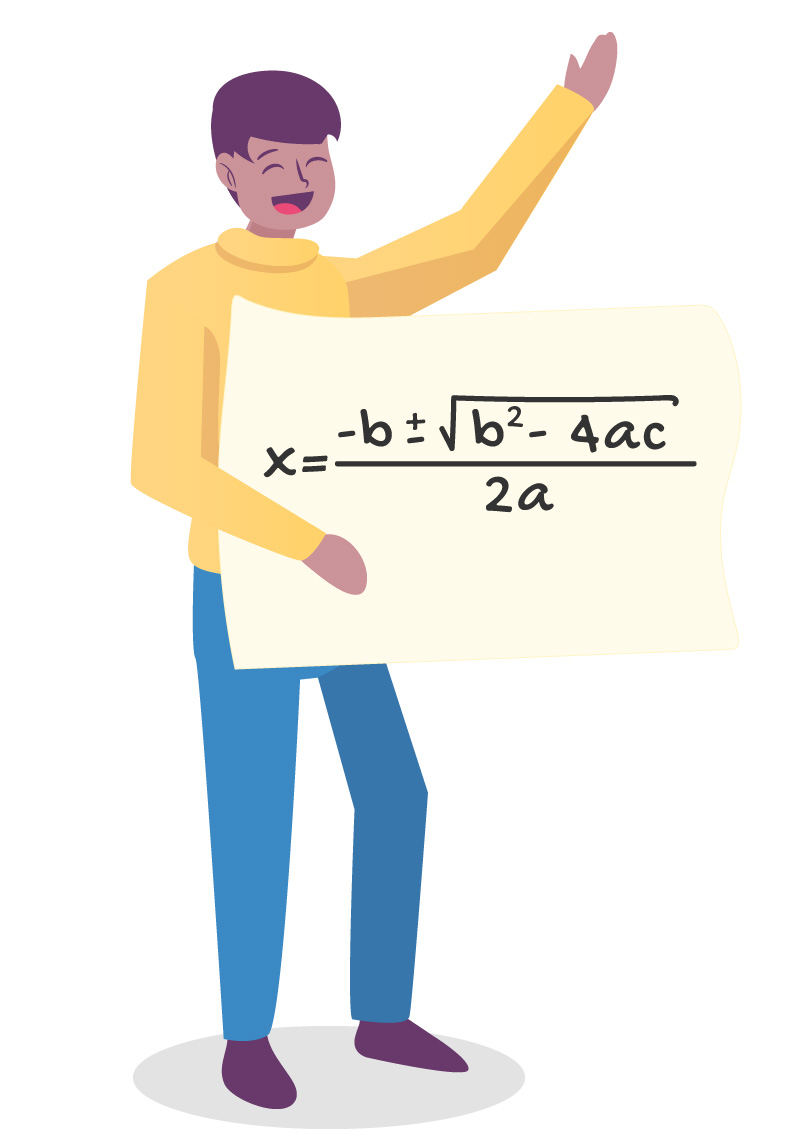
Como comentamos no início do texto, o método da soma e produto pode facilitar e agilizar muito a obtenção das raízes de uma equação do 2º grau, principalmente quando estas são números inteiros. Contudo, quando as raízes são fracionárias ou complexas, fica difícil ou até mesmo impossível defini-las através deste método.

 

3.1 Quando pelo menos uma das raízes é uma fração ou um número decimal

Para entendermos direitinho quando o método da soma e produto não é o mais indicado, vamos tentar seguir os passos apresentados anteriormente para encontrar as raízes da equação 2x² + 3x – 5 = 0. Vejam só o que irá acontecer!

Dada a equação 2x² + 3x – 5 = 0, sabemos que a = 2, b = 3 e c = – 5. Portanto, o quociente – b/a é igual a – 3/2 e o quociente c/a é igual a – 5/2. Assim, chegamos as seguintes relações:

x₁ + x₂ = – 3/2

x₁ ∙ x₂ = – 5/2.

E aí, pessoal, quais são os números reais que somados resultam em – 3/2 e que multiplicados resultam em – 5/2? Quem já praticou muito o método da soma e produto ou tem facilidade com a soma e a multiplicação de frações, vai identificar que as raízes x₁ e x₂ que procuramos valem 1 e – 5/2. Mas, para muitos alunos, esses resultados podem não ser tão claros, principalmente de forma rápida.

 

3.2 Quando as raízes da equação do 2º grau são números complexos

Dada a equação – x² + 2x – 2 = 0, sabemos que a = – 1, b = 2 e c = – 2. Portanto, o quociente – b/a é igual a 2 e o quociente c/a também é igual a 2. Assim, chegamos as seguintes relações:

x₁ + x₂ = 2

x₁ ∙ x₂ = 2.

E agora, vocês sabem dizer quais são os dois números reais que somados e multiplicados resultam em 2? Um tanto estranho, não é mesmo? A verdade, pessoal, é que as raízes desta equação não são números reais, mas sim, números complexos, um assunto no qual não nos aprofundaremos aqui. Por isso, não ficou evidente nenhuma possibilidade real que pudesse satisfazer as duas relações ao mesmo tempo. Em forma de conjunto solução, podemos representar essa situação através de um conjunto vazio.

S = {   }

Tendo esses exemplos em vista, pessoal, quando vocês resolvem usar o método da soma e produto, mas percebem que a solução para as relações de soma e produto não é tão óbvia, não hesitem em abandonar o método e utilizar logo a fórmula de Bhaskara! A partir do cálculo do discriminante da função quadrática (∆), é possível saber se as raízes da equação são reais e iguais, reais e distintas ou mesmo complexas. O método da soma é produto é válido quando agiliza o cálculo das raízes, do contrário, o ideal é utilizar a fórmula de Bhaskara mesmo.

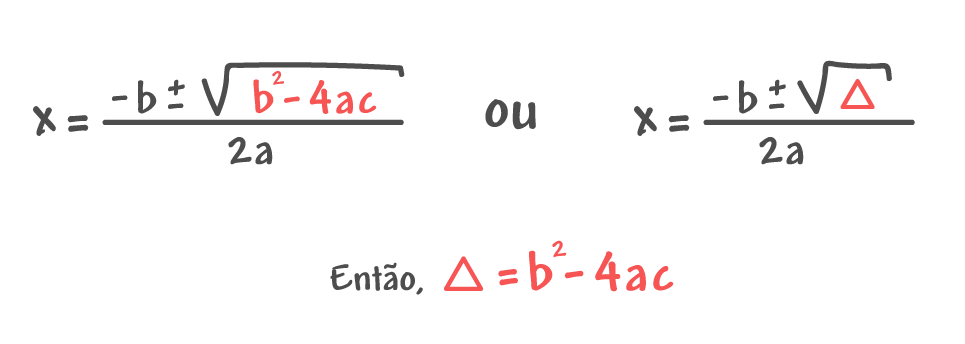
Você sabe como utilizar a fórmula de Bhaskara no cálculo das raízes de uma equação do 2º grau? Não? Então, clique aqui.

Entendido? No próximo item nós vamos resolver mais algumas equações do 2º grau através do método da soma e produto. Vem comigo!

 

4. EQUAÇÕES DO 2º GRAU RESOLVIDAS PELO MÉTODO DA SOMA E PRODUTO

No conjunto ℝ, resolva as seguintes equações:

 

x² + 3x – 10 = 0

Dada a equação x² + 3x – 10 = 0, sabemos que a = 1, b = 3 e c = – 10. Portanto, o quociente – b/a é igual a – 3 e o quociente c/a é igual a – 10. Assim, chegamos as seguintes relações:

x₁ + x₂ = – 3

x₁ ∙ x₂ = – 10.

Agora, é hora de elencarmos algumas possibilidades de números inteiros que multiplicados resultam em – 10.

– 1 x 10 ou 1 x (– 10) = – 10 

– 2 x 5 ou 2 x (– 5) = – 10 

Será que alguma dessas possibilidades vai dar certo na relação de soma? Levando em consideração as regras dos sinais para a adição, parece lógico que a raiz de maior módulo seja negativa, afinal, o resultado da relação de soma deve ser um valor negativo. De qualquer forma, vamos conferir!

– 1 + 10 = 9 

1 – 10 = – 9 

– 2 + 5 = 3 

2 – 5 = – 3 

Perfeito! Isso significa que as raízes x₁ e x₂ da equação x² + 3x – 10 = 0 são iguais a – 5 e 2.

– 5 + 2 = – 3

– 5 ∙ 2 = – 10

S = {– 5, 2}

 

x² – x – 6 = 0

Dada a equação x² – x – 6 = 0, sabemos que a = 1, b = –1 e c = – 6. Portanto, o quociente – b/a é igual a 1 e o quociente c/a é igual a – 6. Assim, chegamos as seguintes relações:

x₁ + x₂ = 1

x₁ ∙ x₂ = – 6.

Mais uma vez, levando em conta as regras dos sinais para a multiplicação, temos as seguintes possibilidades de números inteiros que satisfazem a relação de produto estabelecida.

– 1 x 6 ou 1 x (– 6) = – 6 

– 2 x 3 ou 2 x (– 3) = 6 

E aí, só de olhar, vocês conseguem perceber qual das possibilidades vai satisfazer a relação de soma estabelecida também? Vamos aos testes!

– 1 + 6 = 5 

1 – 6 = – 5 

– 2 + 3 = 1 

2 – 3 = – 1 

Assim, as raízes x₁ e x₂ da equação x² – x – 6 = 0 só podem ser iguais a – 2 e 3.

– 2 + 3 = 1

– 2 ∙ 3 = – 6

S = {– 2, 3}

 

x² – 8x + 16 = 0

Dada a equação x² – 8x + 16 = 0, sabemos que a = 1, b = – 8 e c = 16. Portanto, o quociente – b/a é igual a 8 e o quociente c/a é igual a 16. Assim, chegamos as seguintes relações:

x₁ + x₂ = 8

x₁ ∙ x₂ = 16.

Vamos listar as possibilidades de números inteiros que multiplicados resultam em 16:

1 x 16 = 16

2 x 8 = 16

4 x 4 = 16.

Essa ficou fácil, não é, pessoal? De qualquer forma, vamos fazer todos os testes para conferir.

1 + 16 = 17 

2 + 8 = 10 

4 + 4 = 8 

Desse modo, as raízes x₁ e x₂ da equação x² – 8x + 16 = 0 são reais e iguais a 4.

4 + 4 = 8

4 ∙ 4 = 16

S = {4}

 

Finalizando com super dicas!

 

 

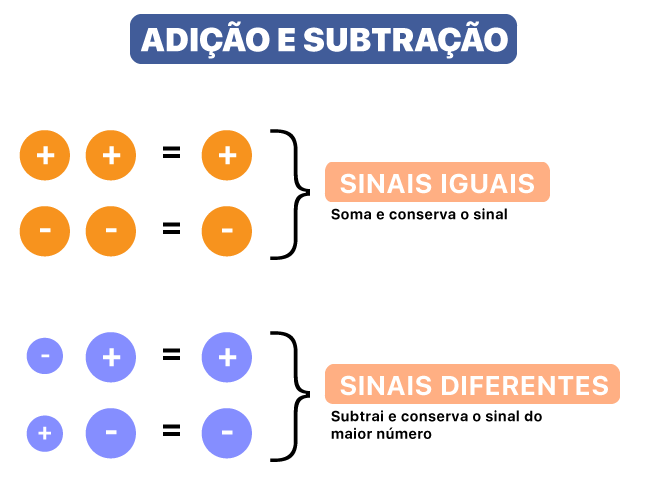
Para resolver cada uma das equações do segundo grau apresentadas neste texto, nós falamos muito das regras dos sinais para a adição e para a multiplicação. Por isso, disponibilizei logo acima essas regras para vocês. É muito importante dominá-las, não só para o estudo do método da soma e produto, como para todo e qualquer assunto que envolve as ciências exatas!

Gostou desse conteúdo? Clique aqui para saber como a Plataforma do Professor Ferretto funciona!

Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!

Certo, pessoal? Logo abaixo deixo um vídeo que traz toda a explicação sobre o método da soma e produto e também sobre a determinação das equações do 2º grau. Espero vocês por lá!

Um abraço a todos, sucesso nos estudos e até mais!