FRAÇÕES EQUIVALENTES E A SIMPLIFICAÇÃO DE FRAÇÕES
24/01/2020
Quando duas frações representam a mesma quantidade, elas são consideradas frações equivalentes, mesmo que sejam aparentemente diferentes. Além disso, existem algumas frações que não conseguimos simplificar. Estas são conhecidas como frações irredutíveis.
Olá, pessoal! Tudo bem por aí?
Nós já estudamos aqui no blog o conceito de fração, e o que são frações próprias, impróprias, mistas e aparentes. Neste texto, nós vamos complementar este estudo com mais alguns conceitos muito importantes para quem é estudante do ensino médio e/ou pretende prestar as provas do ENEM e dos vestibulares logo mais. Vamos conhecer as frações equivalentes, as frações irredutíveis e também o processo de simplificação de frações. Por fim, para podermos comparar frações diferentes com segurança, aprenderemos a reduzir frações a um mesmo denominador.
Feito, pessoal?! Então, vamos começar!
1. O QUE SÃO FRAÇÕES EQUIVALENTES?
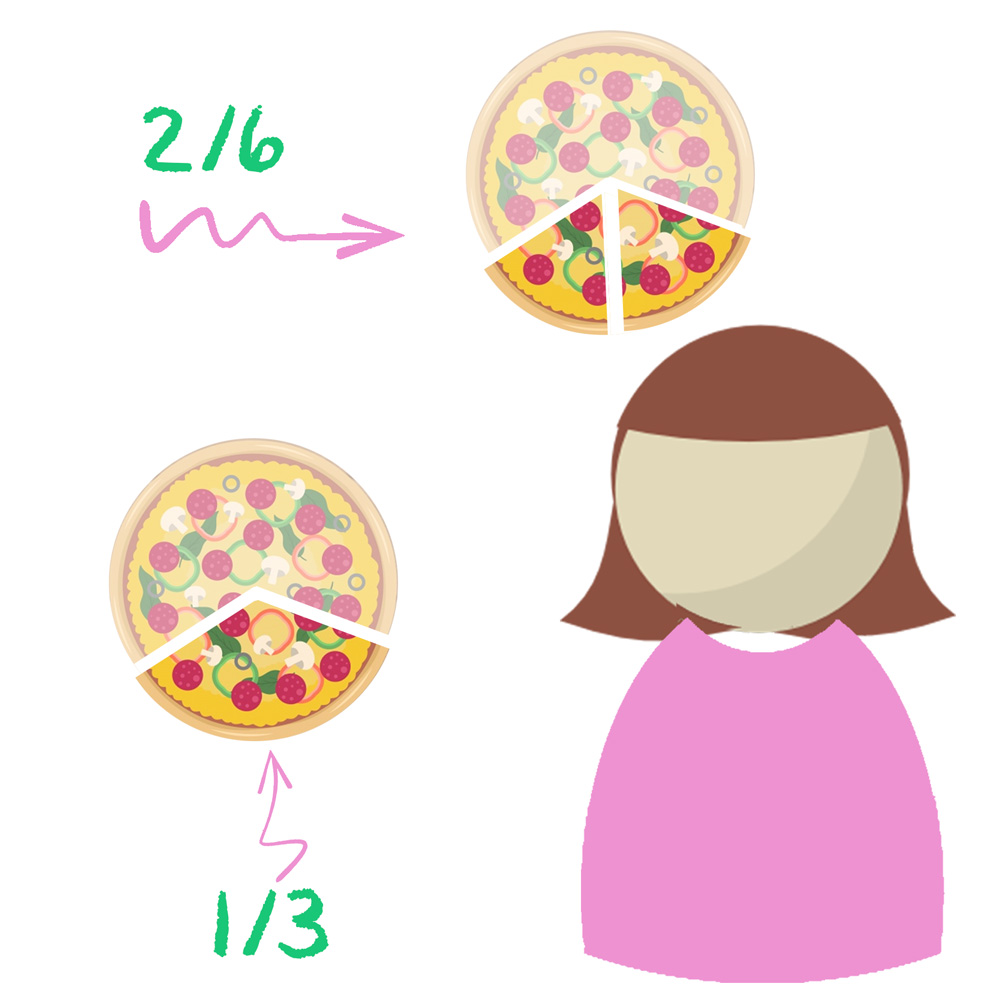
Duas ou mais frações são consideradas equivalentes, quando representam a mesma quantidade ou a mesma parte de um todo, muito embora sejam aparentemente diferentes.
A imagem abaixo mostra o conceito de forma mais clara. Reparem que os círculos estão divididos de forma diferente, e que partes diferentes do todo foram tomadas. Contudo, no fim das contas, a metade do círculo foi pintada em todos os casos.
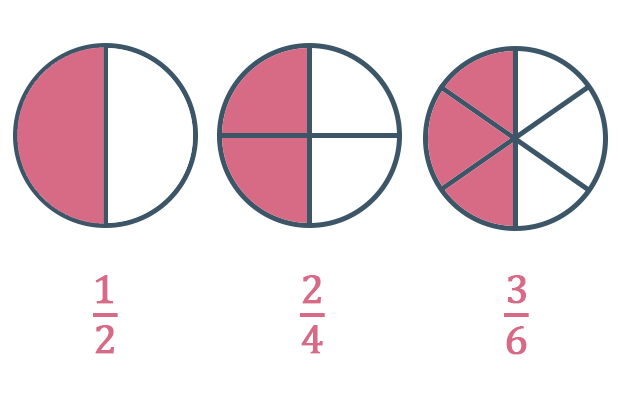
Assim, é possível concluir que apesar das frações 1/2, 2/4 e 3/6 serem aparentemente diferentes, elas representam a mesma quantidade, que é, em suma, 1/2. Por isso, elas são consideradas frações equivalentes.
Se observarmos novamente as três frações com atenção, veremos, por exemplo, que podemos obter a fração 2/4 multiplicando o numerador e o denominador da fração 1/2 por 2. De forma semelhante, é possível encontrar 3/6 multiplicando o numerador e o denominador da fração 1/2 por 3. Tudo isso nos permite concluir que as frações equivalentes são sempre múltiplas umas das outras.
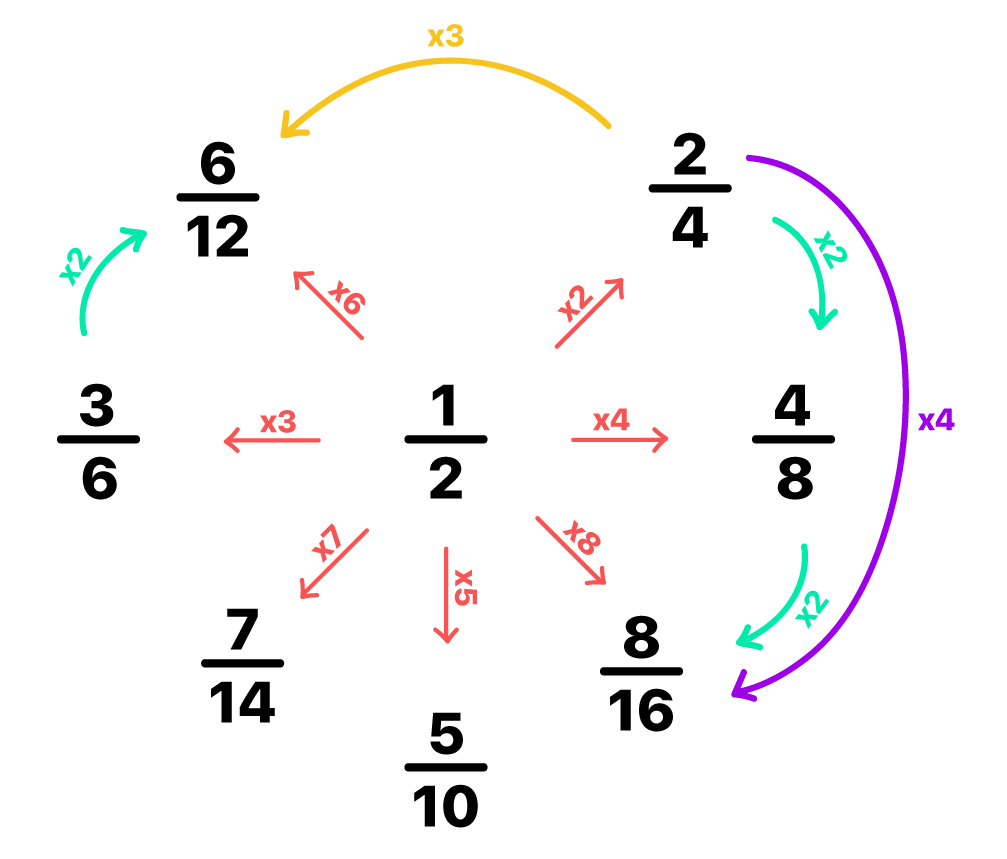
Entendido, pessoal? Pois então, assim como podemos obter frações equivalentes de uma determinada fração multiplicando seu numerador e seu denominador por um valor comum, também podemos fazer isso de uma segunda maneira: simplificando uma fração que não seja irredutível. Venham comigo até o próximo item para entender melhor esse caso!
2. COMO FAZER A SIMPLIFICAÇÃO DE FRAÇÕES?
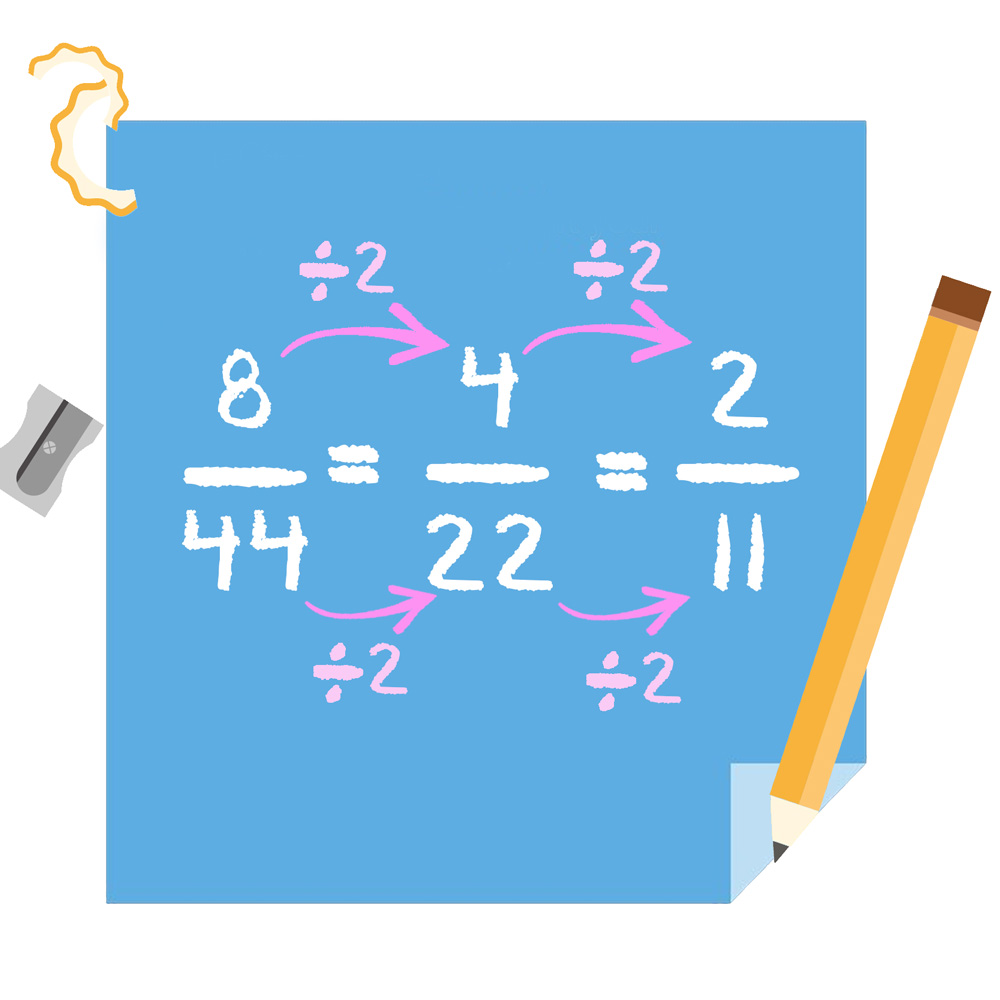
Basicamente, simplificar uma fração consiste em dividir numerador e denominador pelo mesmo número inteiro. O resultado é uma fração equivalente a inicial, só que com valores menores no numerador e no denominador.
Mas como saber por qual número inteiro devemos dividir o numerador e o denominador de uma fração ao simplifica-la? A maneira mais simples e mais comum de se fazer isso consiste em observar o numerador e o denominador da fração e encontrar um número inteiro que possa dividir os dois termos sem deixar resto. Vamos aplicar essa técnica simplificando a fração 8/20.

Ao observar a fração 8/20, vocês poderiam ter lembrado que tanto 8 quanto 20 são divisíveis por 2, ou então que ambos são divisíveis por 4. As duas simplificações estão corretas! Contudo as frações equivalentes geradas em cada um dos casos possuem uma diferença muito intrigante. Vocês descobrem qual é essa diferença comigo, no próximo item.
2.1 Frações Irredutíveis

Quando simplificamos a fração 8/20 por 2, esta gerou a fração equivalente 4/10. Como 4 e 10 também são divisíveis por 2, poderíamos simplificar a fração novamente, chegando à fração equivalente 2/5. Já quando simplificamos a fração 8/20 por 4, obtivemos de forma direta a fração equivalente 2/5. Só que o único divisor comum entre 2 e 5 é o número 1. Quando isso acontece, podemos dizer que a fração encontrada é irredutível, e que não é mais possível simplifica-la.
Então, pessoal, se o objetivo de vocês for simplificar uma fração até obter a fração equivalente irredutível, o jeito é ir dividindo numerador e denominador pelo mesmo fator até encontrar uma fração cujo numerador e denominador possuam como divisor comum apenas o número 1.

Pois então, pessoal, existe sim! E o melhor é que o método utiliza um cálculo muito conhecido na matemática básica. Vamos a uma super dica ninja sobre o assunto, vem comigo!
2.1.1 Dica ninja sobre frações irredutíveis

Através do cálculo do Máximo Divisor Comum (MDC) entre o numerador e o denominador de uma fração, é possível encontrar o número que divide ambos sem deixar resto e nos entrega a fração equivalente irredutível da fração inicial.

Para calcular o MDC entre dois ou mais números é preciso realizar a decomposição em fatores primos desses números. O valor do MDC é dado pelo produto entre os fatores que dividiram a linha inteira na decomposição. Reparem que assinalamos (*) no exemplo acima apenas os números que dividiram a linha inteira, ou seja, que dividiram ao mesmo tempo todos os elementos da decomposição. Assim, podemos concluir que o MDC entre 20 e 8 é:
2 ‧ 2 = 4
Lembram que quando dividimos o numerador e o denominador da fração 8/20 por 4, obtivemos diretamente a fração equivalente irredutível 2/5? Isso significa que utilizar o MDC para chegar as frações irredutíveis é um método válido. Inclusive, esse conhecimento nos permite definir as frações irredutíveis sob um segundo ponto de vista, olhem só!
Uma fração a/b é irredutível quando o máximo divisor comum entre o numerador a e o denominador b é igual a 1.
Incrível, não é? Pois bem, agora que já sabemos tudo sobre a simplificação de frações e as frações irredutíveis, que tal aprendermos a comparar o valor de determinadas frações? Observando as frações 5/8 e 7/12, sem dividir, vocês sabem dizer qual delas representa o maior valor numérico? Quem não sabe, precisa vir comigo até o próximo item. Vamos lá!
3. COMPARAÇÃO DE FRAÇÕES
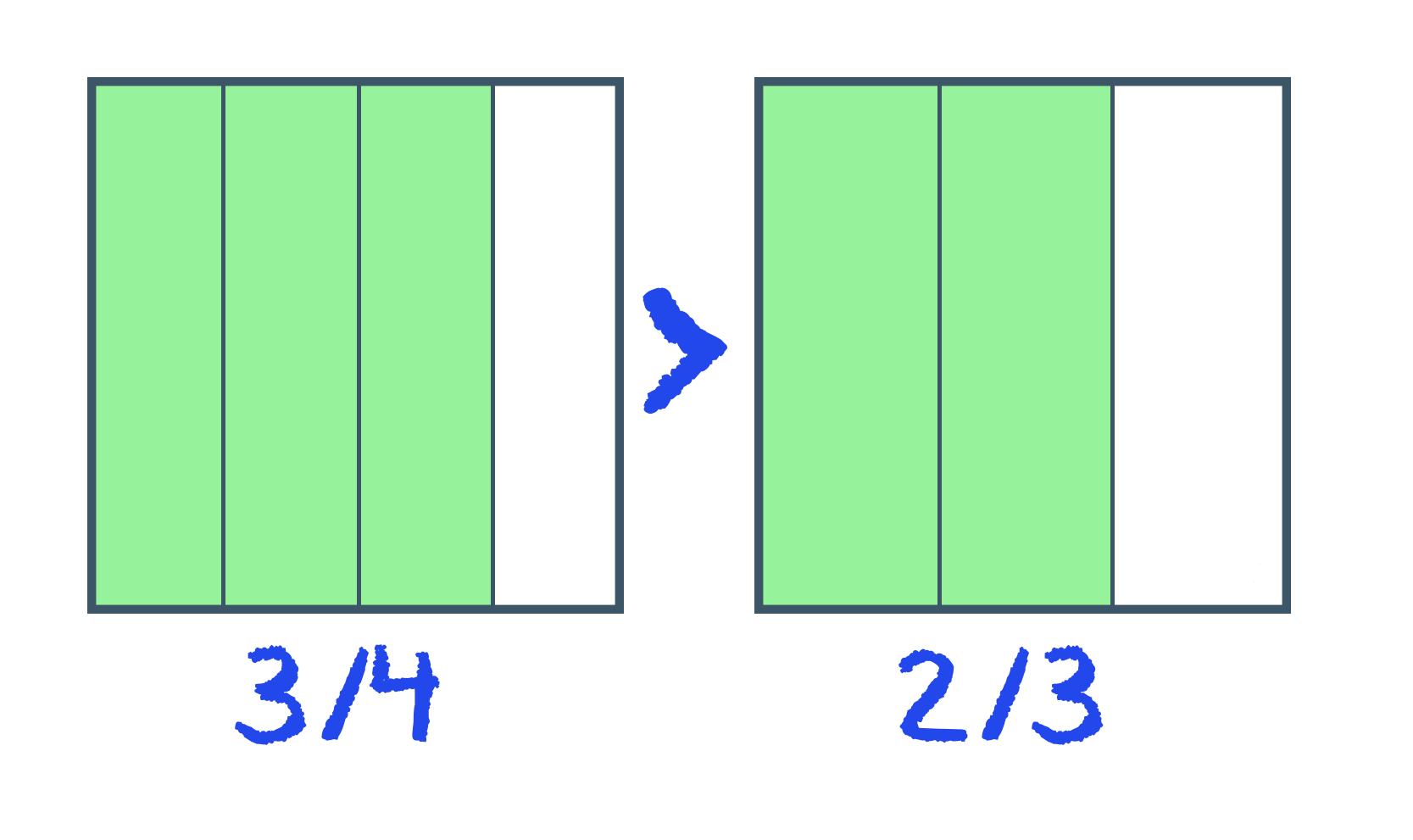
Quando duas ou mais frações possuem o mesmo denominador, torna-se muito simples determinar qual delas representa o maior ou o menor valor numérico. Se os denominadores já são iguais, basta comparar os numeradores das frações.
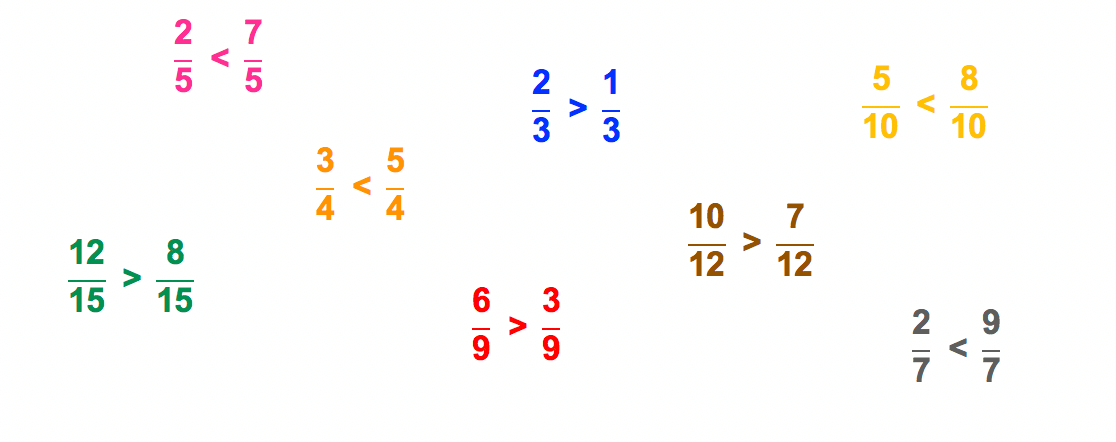
Ao observar as frações 2/5 e 7/5, por exemplo, não resta dúvidas de que 7/5 representa um valor numérico maior que a fração 2/5. Isso porque 7 é um valor maior que 2.
Contudo, quando duas ou mais frações possuem denominadores diferentes, não há como saber qual delas representa o maior ou o menor valor numérico somente a partir de observações. Nesse caso, é necessário reduzir as frações a um mesmo denominador antes de realizar qualquer tipo de observação. Vamos ver como isso funciona no próximo item.
3.1 Redução de frações a um mesmo denominador
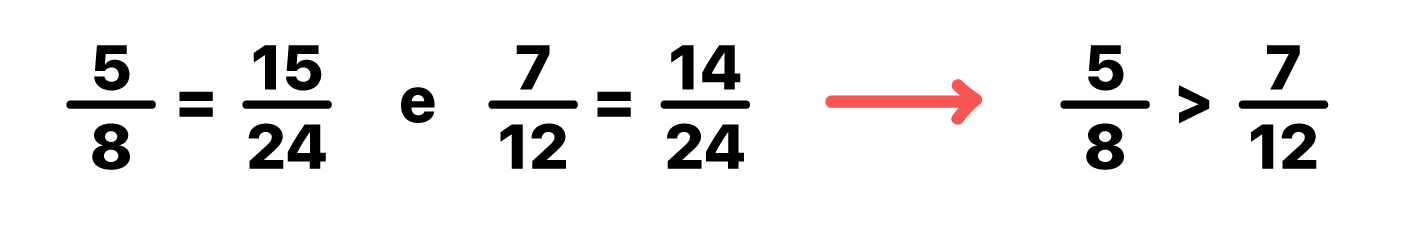
Dois passos simples nos permitem reduzir duas ou mais frações a um mesmo denominador. Vamos estudar cada um deles a partir de um exemplo. Vem comigo!
1º Passo: calcular o MMC entre os denominadores das frações
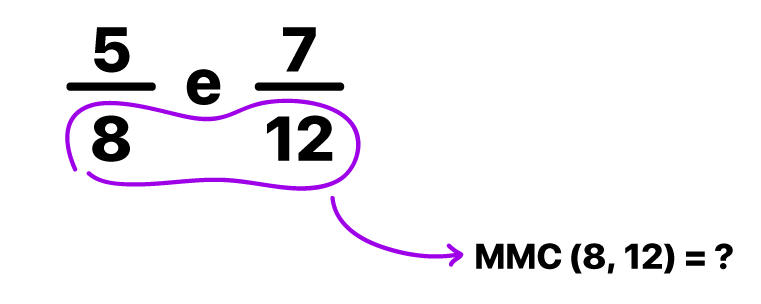
O cálculo do mínimo múltiplo comum (MMC) também se utiliza da famosa decomposição simultânea em fatores primos. Feita a decomposição entre dois ou mais números, o MMC pode ser obtido através do produto entre os fatores primos resultantes. Vamos calcular o MMC entre os denominadores 8 e 12 para que a ideia fique mais clara.
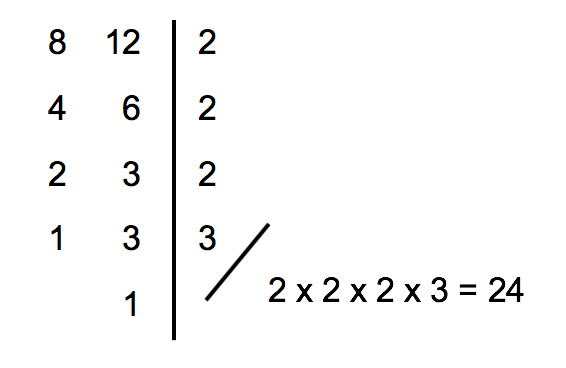
2º Passo: calcular os numeradores equivalentes das frações
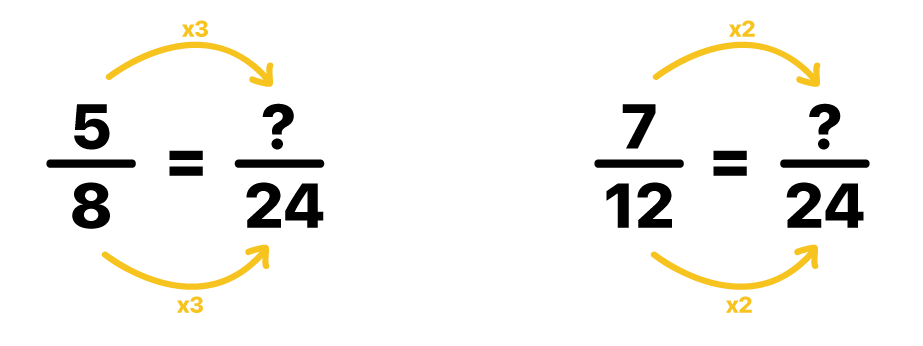
Depois de realizar o cálculo do MMC e conhecer o denominador comum entre as frações que estão sendo comparadas, é necessário encontrar também os respectivos numeradores que tornam as frações equivalentes. Aí é só pensar no seguinte: se o denominador de uma das frações era 8 e agora é 24, ele foi multiplicado por 3. Então, devemos multiplicar o numerador por 3 também. Na outra fração o denominador era 12 e agora é 24, ou seja, ele foi multiplicado por 2. Assim, da mesma forma que na fração anterior, devemos multiplicar o numerador por 2.
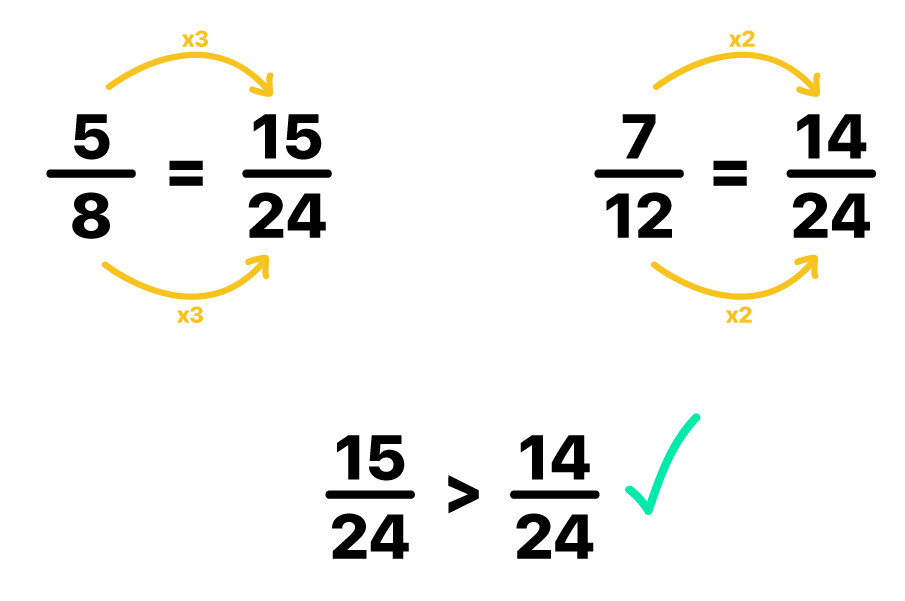
Pronto! Agora é possível ver que a fração 15/24 é maior que a fração 14/24. Consequentemente, a fração 5/8 é maior do que a fração 7/12.
E aí, o que acharam dos conteúdos que acabamos de estudar? Se você gostou do texto, aproveite para clicar aqui e saber como a plataforma do Professor Ferretto funciona!
Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!
Pessoal, espero que esse conteúdo tenha ajudado vocês a compreender um pouco mais do universo das frações. Quem quiser complementar os estudos, não pode deixar de ver o vídeo que se encontra logo abaixo. Vamos resolver juntos mais uma série de exemplos sobre simplificação e redução de frações a um mesmo denominador.
Aguardo vocês no próximo post! Um abraço e até mais!