As relações métricas no triângulo retângulo são expressões matemáticas que relacionam as medidas de alguns elementos do triângulo retângulo. Dentre esses elementos, destacam-se a hipotenusa, os catetos, a altura relativa à hipotenusa e as projeções dos catetos sobre a hipotenusa dos triângulos retângulos.

 

Olá, pessoal! Tudo bem com vocês?

O triângulo retângulo é uma das figuras geométricas mais conhecidas e utilizadas na geometria plana. Por isso, jamais poderíamos deixar de estudar as suas relações métricas! Neste texto, nós vamos conhecer uma série dessas relações com base no conceito de semelhança entre triângulos retângulos. Esse é outro conhecimento muito importante para quem deseja realizar as provas do ENEM e/ou de alguns vestibulares.

Beleza, pessoal?! Então, já que as relações métricas relacionam as medidas dos elementos do triângulo retângulo, o jeito é conhecermos cada um desses elementos. Venham comigo!

 

1. ELEMENTOS DE UM TRIÂNGULO RETÂNGULO

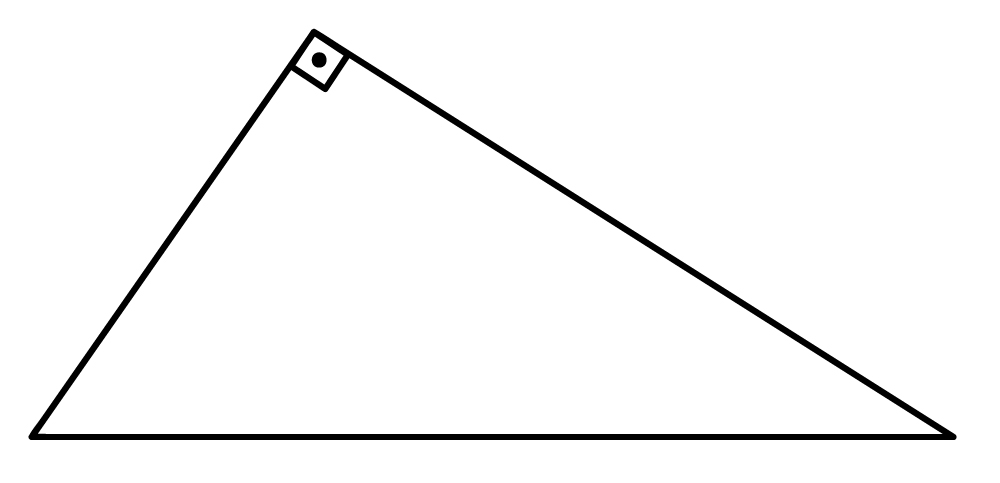
Observem a imagem acima. Nela, podemos ver um polígono de 3 lados em que um de seus ângulos internos é conhecido e mede 90º (ângulo reto). Esse é um exemplo de triângulo retângulo. Vamos tomá-lo como base para definir os elementos listados a seguir. Sigam comigo!

 

1.1 Hipotenusa

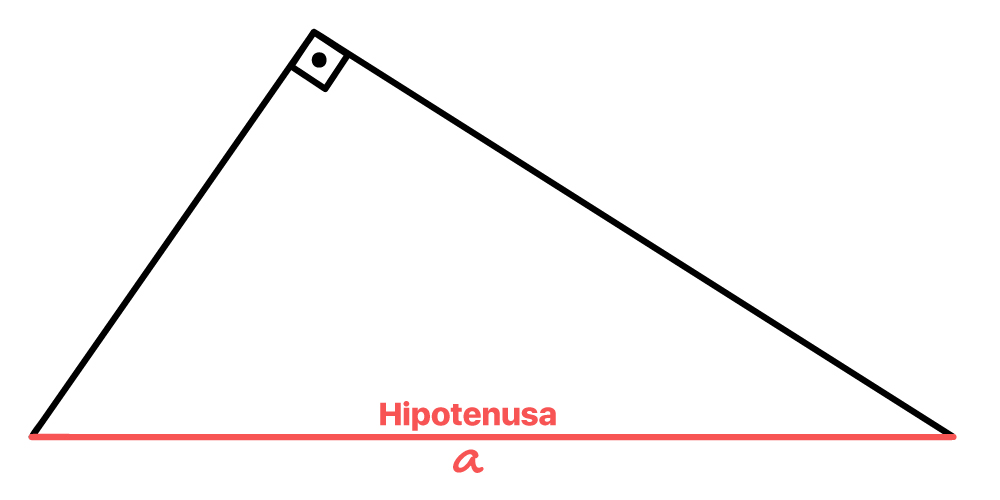
A hipotenusa, representada pela letra a, é sempre o maior lado do triângulo retângulo. Também podemos dizer que a hipotenusa é o lado oposto ao ângulo de 90º.

 

1.2 Catetos

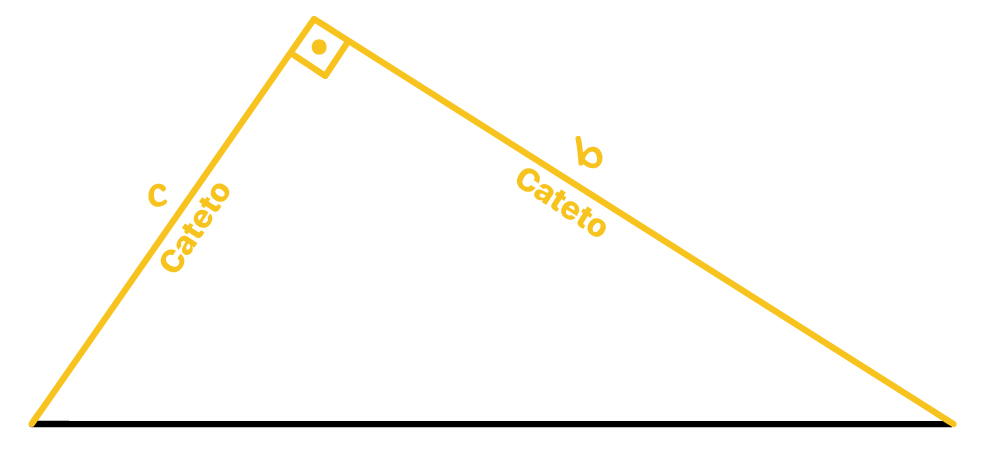
Os outros dois lados menores do triângulo retângulo, representados pelas letras c e b, são conhecidos como catetos. Estes lados são perpendiculares entre si, por isso podemos dizer que eles formam o ângulo de 90º.

 

1.3 Altura relativa à hipotenusa

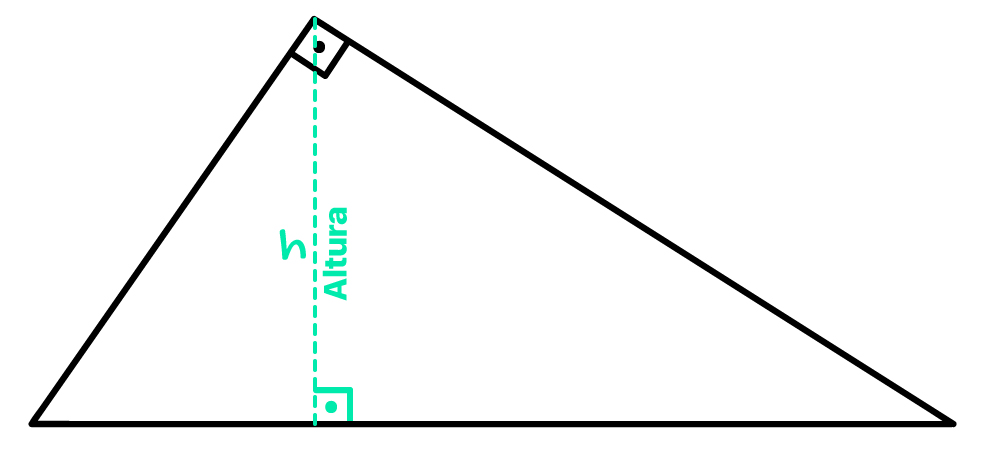
O segmento pontilhado apresentado na imagem acima representa a altura h do triângulo retângulo quando a hipotenusa é considerada a sua base. Por isso se fala em altura relativa à hipotenusa. Reparem que esse segmento é perpendicular a hipotenusa, ou seja, ele forma um ângulo de 90º com ela.

 

1.4 Projeções dos catetos sobre a hipotenusa

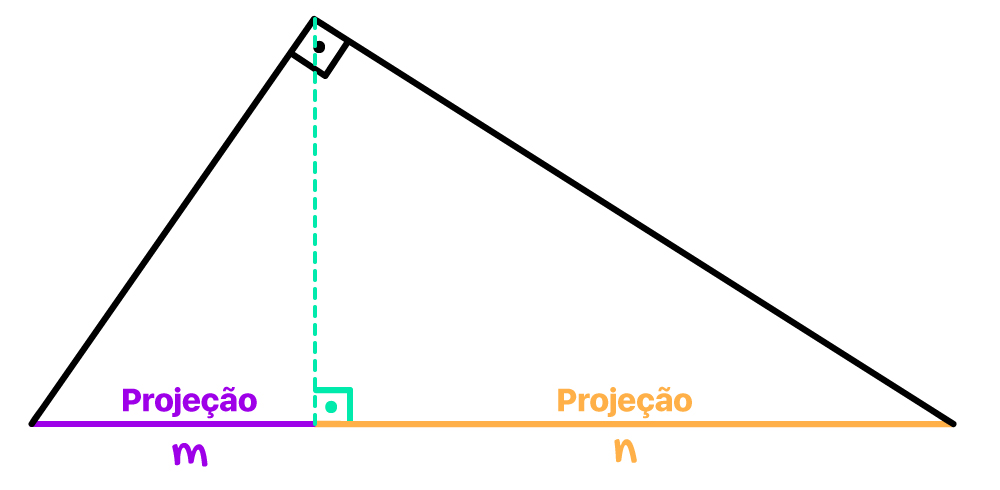
As letras m e n representam as projeções dos catetos c e b sobre a hipotenusa. A fim de jamais esquecermos esses dois elementos tão importantes do triângulo retângulo, vamos imaginar as seguintes situações.

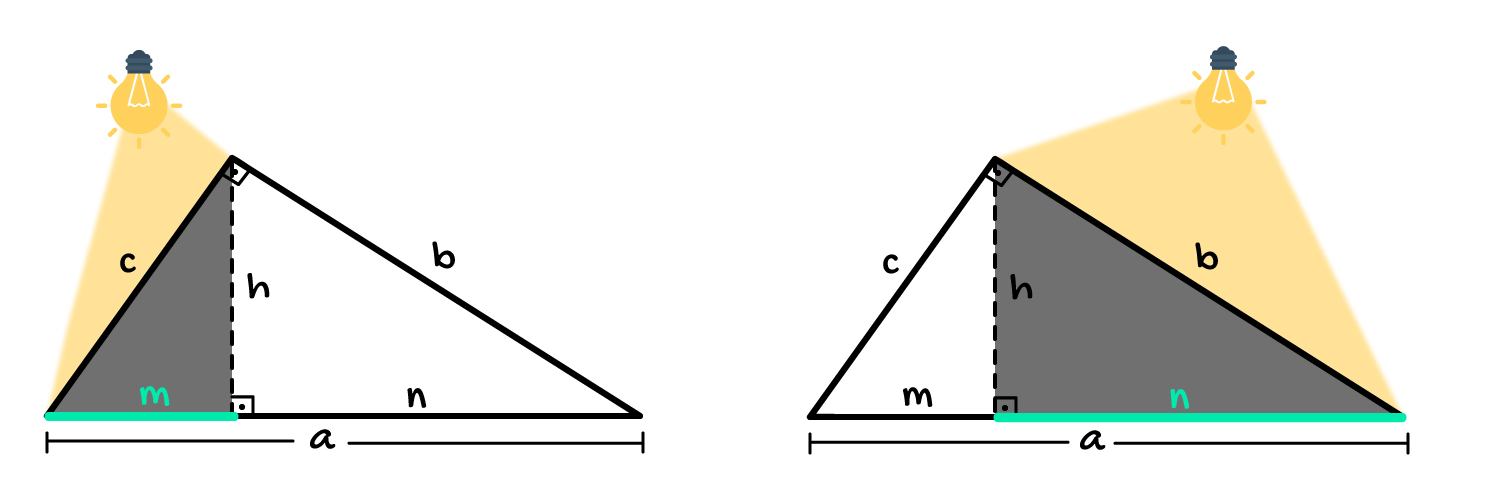
Se uma luz incidisse de cima sobre o cateto c do triângulo retângulo, este geraria uma sombra de comprimento m sobre a hipotenusa. Do mesmo modo, se o evento ocorresse sobre o cateto b, este geraria uma sombra de comprimento n sobre a hipotenusa. Por isso, diz-se que m é a projeção do cateto c sobre a hipotenusa, da mesma forma que n é a projeção do cateto b sobre a hipotenusa.

Incrível, não é mesmo? Agora que vocês conhecem os principais elementos do triângulo retângulo, vamos estudar juntos o conceito de semelhança entre triângulos retângulos. Vem comigo!

 

2. TRIÂNGULOS RETÂNGULOS SEMELHANTES

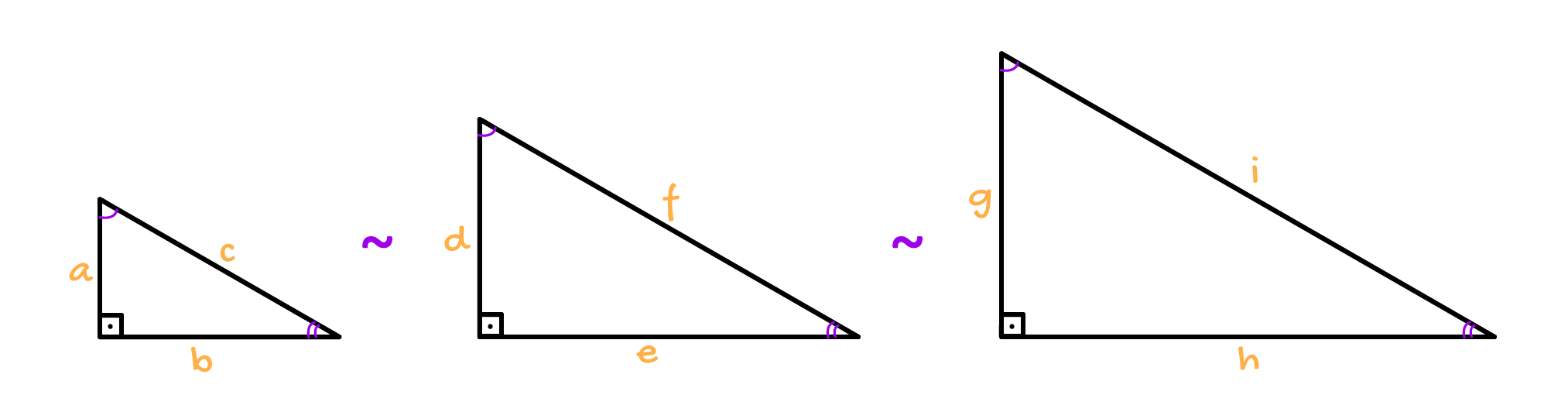
Dois ou mais triângulos são considerados semelhantes quando seus ângulos correspondentes são congruentes e os lados homólogos são proporcionais. Reparem na imagem acima, que os lados dos três triângulos retângulos são proporcionais, e que os 3 ângulos internos de cada um deles possuem o mesmo valor: 90º, “linha” e “duas linhas”.

Quando se trata do triângulo retângulo, um ângulo interno é sempre de valor definido, porque como vimos, seus dois catetos formam um ângulo reto (90º). Assim, considerando que a soma dos ângulos internos de todo triângulo é sempre igual a 180º, é fato que os outros dois ângulos internos do triângulo retângulo, que são agudos, devem somar juntos outros 90º. Isso nos permite fazer a seguinte afirmação:

Em um triângulo retângulo os ângulos agudos são sempre complementares.

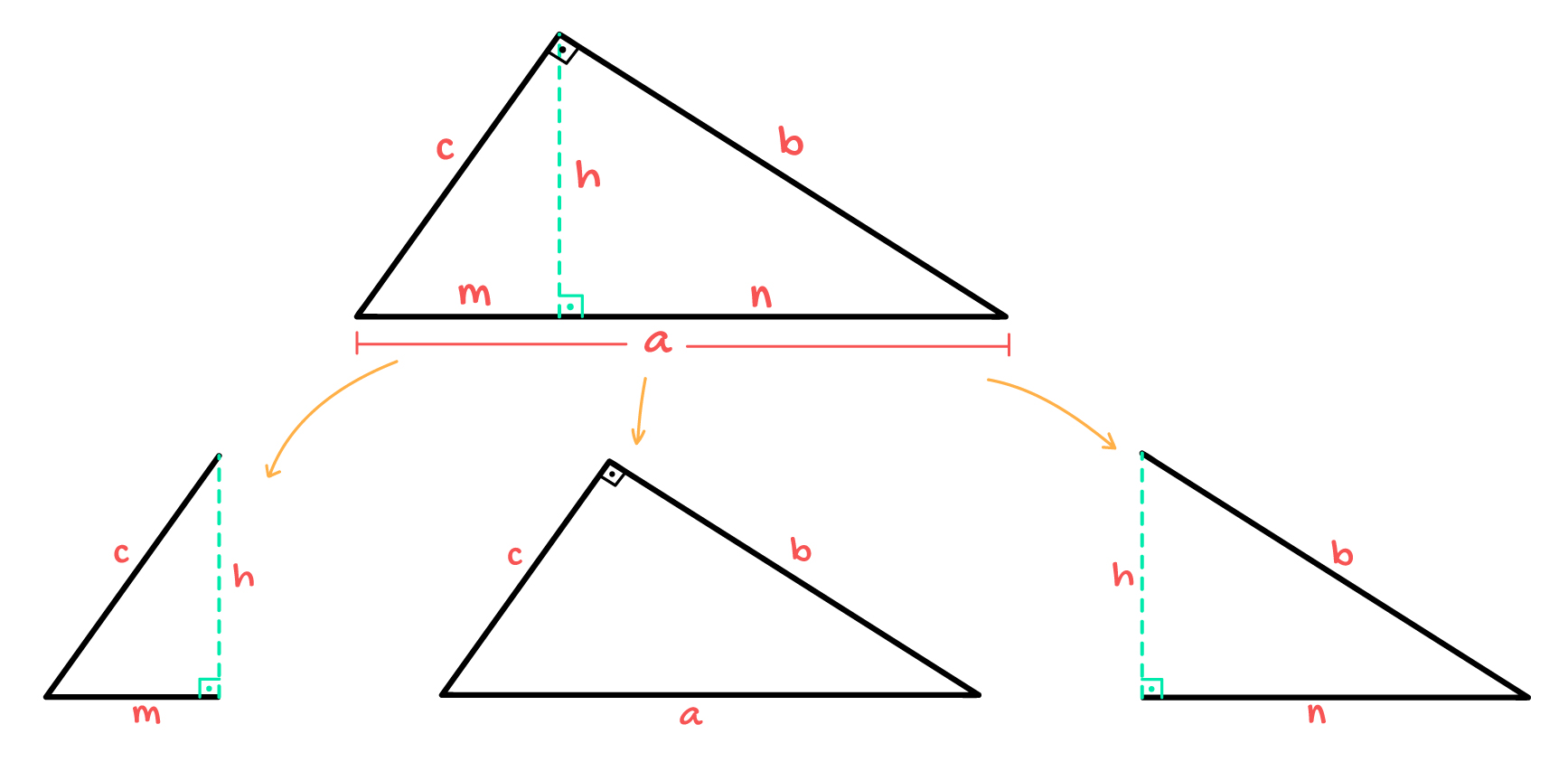
Pensando nesses conceitos, nós vamos voltar ao nosso triângulo retângulo inicial e dividi-lo em 3 triângulos retângulos diferentes. O triângulo maior, de lados a, b, e c, o triângulo da esquerda, de lados c, m, e h, e o triângulo da direita, de lados b, h, e n.  Acompanhem comigo no que isso vai dar!

 

2.1 Os primeiros passos rumo às relações métricas no triângulo retângulo

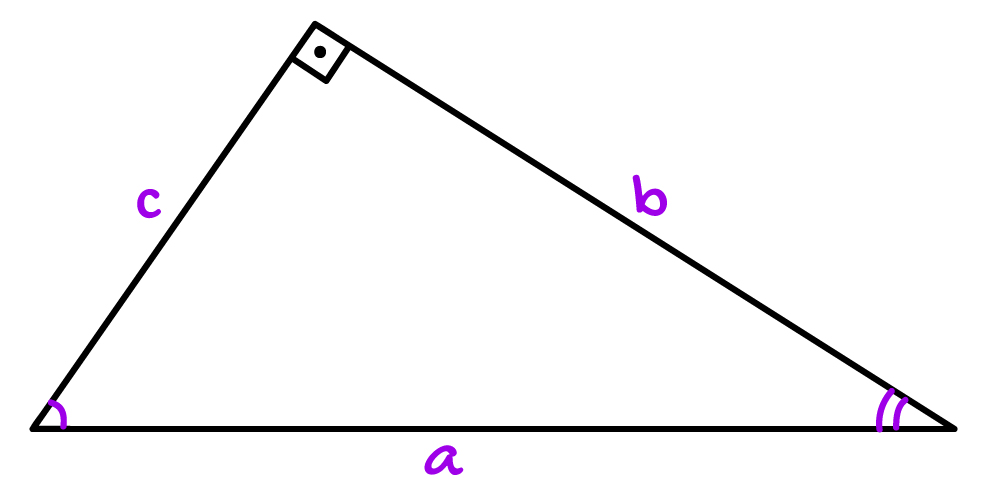
Observando o triângulo de lados a, b e c, podemos dizer, por exemplo, que o ângulo formado entre os lados a e c é de valor “linha”, e que o ângulo formado entre os lados b e a é de valor “duas linhas”.

Sabendo que os demais triângulos são formados a partir do triângulo que acabamos de analisar, podemos concluir que no triângulo da esquerda, o ângulo entre os lados c e m também vale “linha”. Já no triângulo da direita, sabe-se que o ângulo formado entre os lados b e n também vale “duas linhas”.

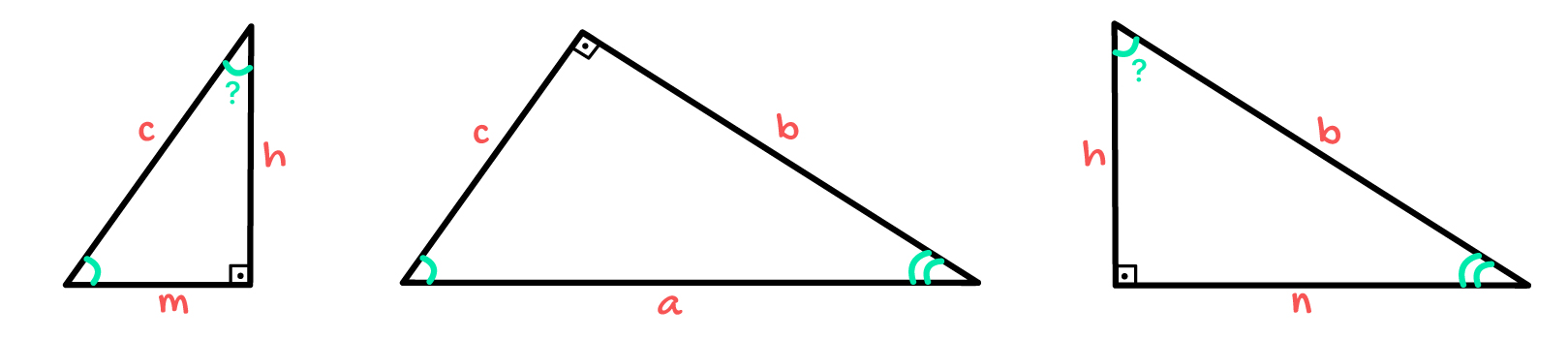
E qual será o valor dos demais ângulos, pessoal? Se em um triângulo retângulo os ângulos agudos são sempre complementares, podemos afirmar com toda a certeza que no triângulo da esquerda, o ângulo formado entre os lados c e h também vale “duas linhas”. Enquanto isso, no triângulo da direita, o ângulo formado entre os lados b e h também vale “linha”.

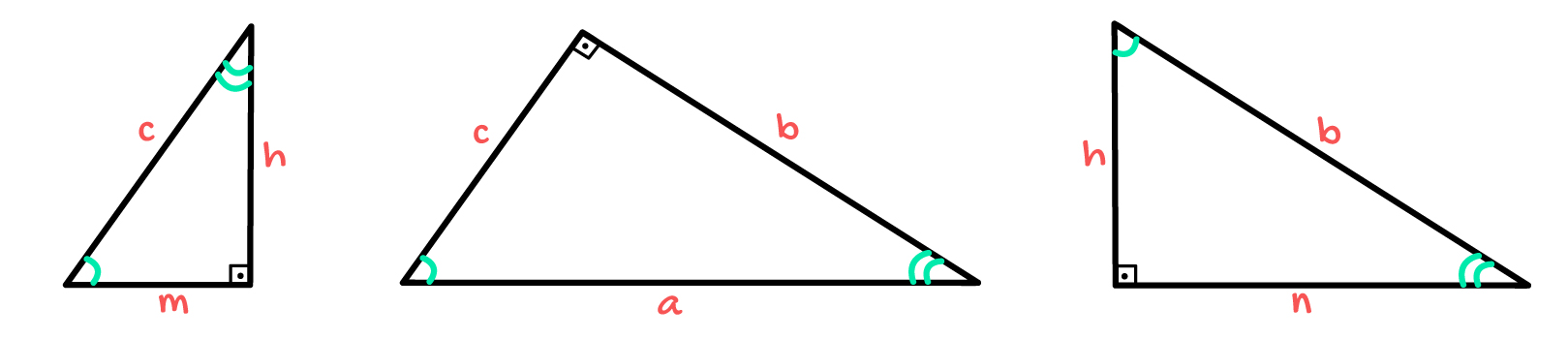
A partir de toda essa análise, é possível concluir que os 3 triângulos formados são semelhantes. Essa característica nos permite encontrar uma série de proporções entre as medidas dos elementos a, b, c, m, n e h. São as relações métricas no triângulo retângulo!

 

3. RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO

 

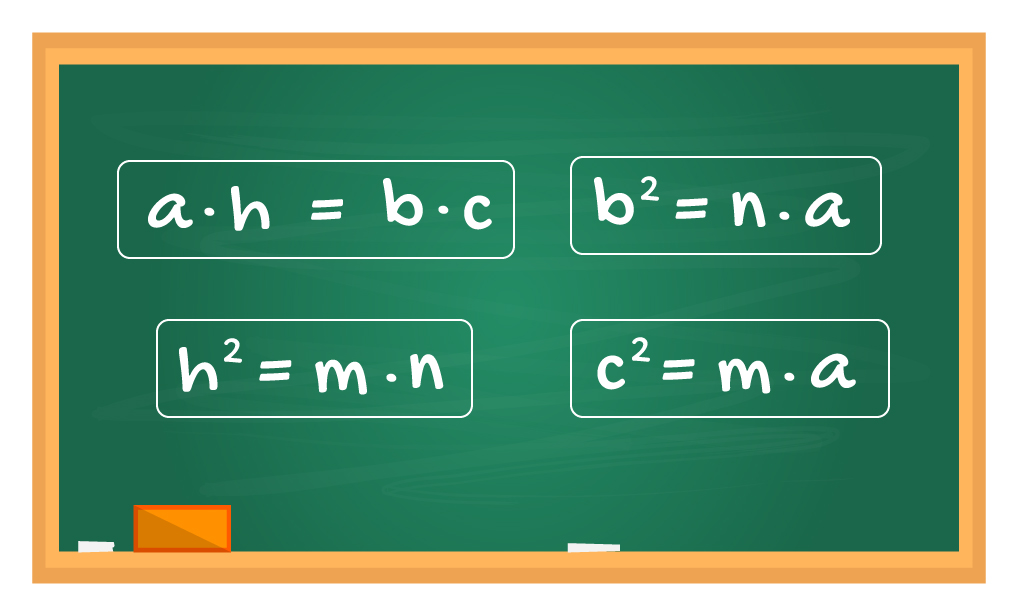
Essas são 4 das principais relações métricas no triângulo retângulo. Nos próximos itens, vocês conferem a origem de cada uma dessas relações. Venham comigo!

 

1ª: O produto entre a hipotenusa a e a altura relativa à hipotenusa h é exatamente igual ao produto entre catetos b e c

 

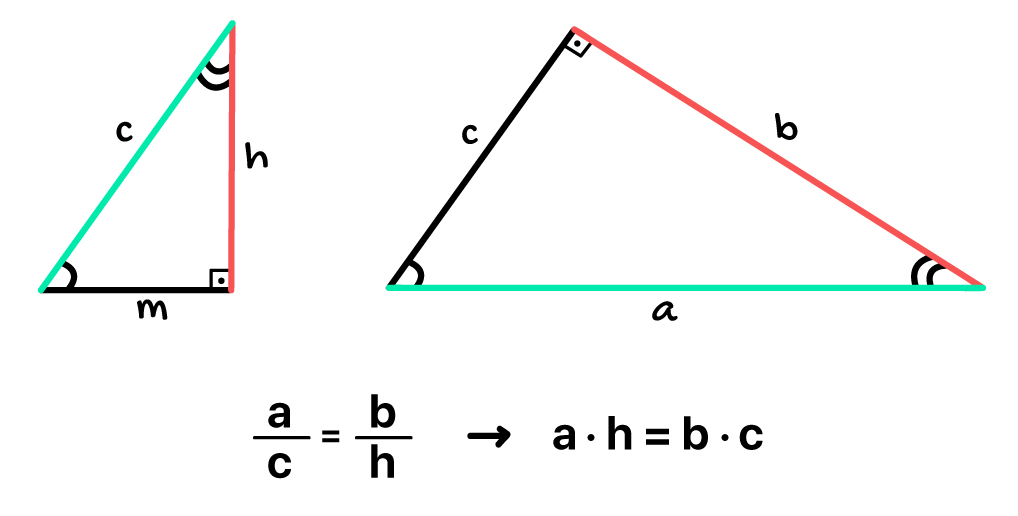
2ª: O quadrado da altura relativa à hipotenusa h é igual ao produto das projeções dos catetos sobre a hipotenusa m e n

 

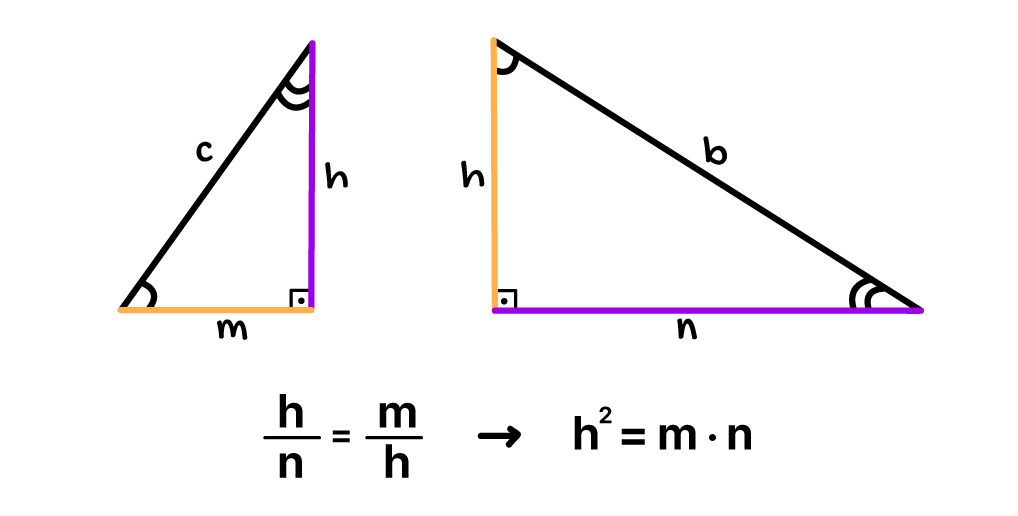
3ª e 4ª: O quadrado da medida de um cateto é sempre igual ao produto entre a sua projeção sobre a hipotenusa e a própria hipotenusa

 

 

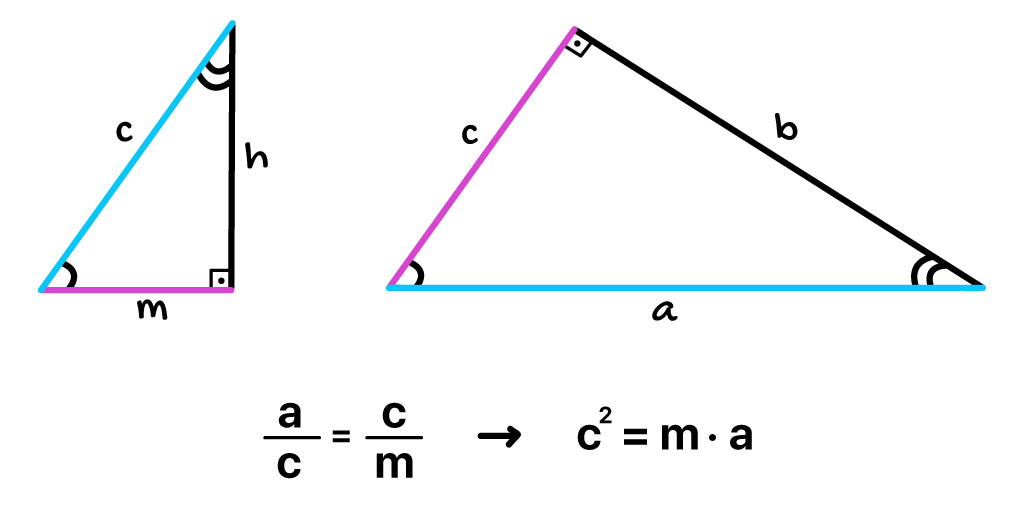
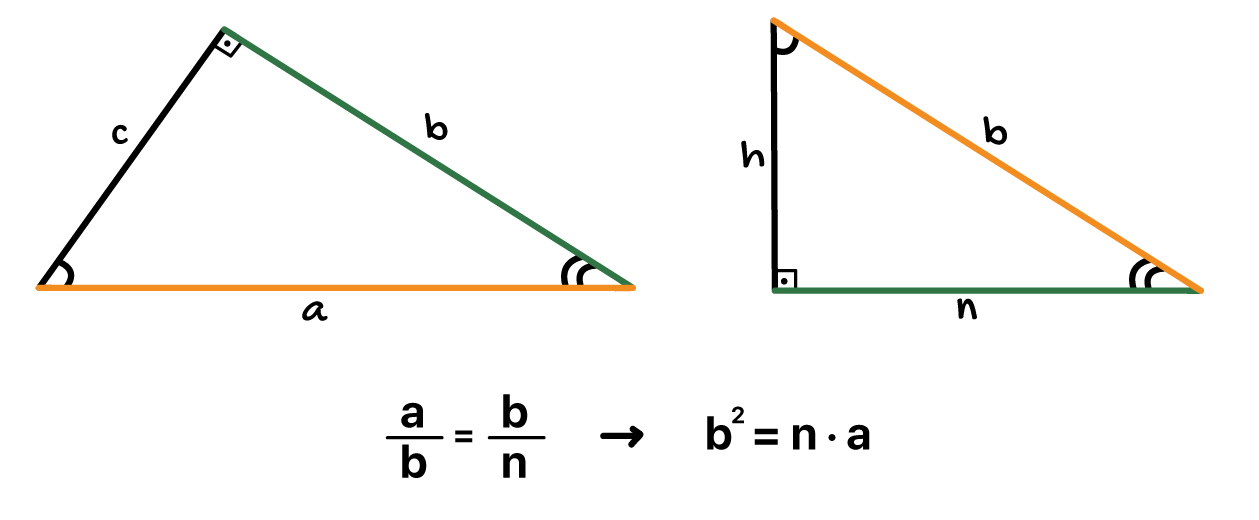
E aí, o que acharam destas relações? Se a forma como cada uma delas foi construída ainda não está clara para vocês, peço que assistam o vídeo que está disponível aqui embaixo. Nele, eu explico cada uma das equações detalhadamente, para não restar mais nenhuma dúvida!

Mas antes de encerrarmos o texto, duas coisas ainda precisam ser ditas. A primeira delas é que existe uma relação métrica muito famosa que ainda não estudamos: o Teorema de Pitágoras! Essa relação é extremamente importante no estudo da geometria, por isso, tem um texto dedicado à ela! Cliquem aqui para conferir!

Além disso, gostaria de fazer um convite a todos que gostaram deste texto. Que tal conhecer a plataforma do Professor Ferretto? Clique aqui para saber como ela funciona!

Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!

Agora sim, finalizamos mais um texto! Espero que ele tenha sido muito proveitoso e colaborativo para os estudos de vocês!

Abraço, muito sucesso e até mais!