TRIÂNGULO EQUILÁTERO
16/05/2018
Olá pessoal! Tudo bem por aí?
Hoje voltaremos a falar sobre geometria plana, e mais especificamente sobre o triângulo equilátero! O triângulo equilátero é assim chamado, porque possui 3 lados e 3 ângulos internos de igual medida. Essas características, nos permitem definir uma série de relações e propriedades bem importantes, e conhecer cada uma delas pode nos ajudar, e muito, a desvendar aquela questão de geometria que costuma ser cobrada nos vestibulares e também nas provas do ENEM!
E aí eu pergunto: a matemática tem sido uma boa aliada, quando o objetivo é tirar um notão nas provas de vestibulares ou do ENEM? Não? Então não percam tempo, assinem a plataforma do Professor Ferretto! Lá é possível encontrar o conteúdo completo de geometria plana e de toda a matemática do ensino médio, além de simulados semanais, exercícios resolvidos em vídeo, e mais uma série de vantagens. Acessem o site para conferir todos os planos disponíveis!
Certo pessoal!? Vamos começar tirando algumas conclusões acerca do esboço de um triângulo equilátero. Vem comigo aqui!
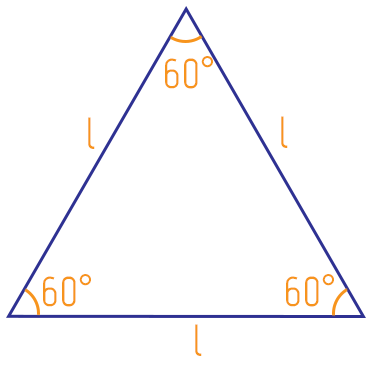
Como nós vimos no início do texto, um triângulo equilátero possui os seus três lados congruentes entre si, ou seja, de mesma medida, que aqui chamaremos de l. Uma consequência disso, é que seus três ângulos internos acabam tendo a mesma medida também. Mas vocês sabem como é possível definir exatamente o valor de cada ângulo interno de um triângulo equilátero?
O fato é que a soma dos ângulos internos de qualquer triângulo deve ser sempre 180º, e como o triângulo equilátero possui 3 ângulos internos iguais, basta dividirmos 180º por 3, e teremos, finalmente, o valor de cada ângulo em si. Bom, 180º/3 = 60º, e isso explica porque cada um dos ângulos internos de um triângulo equilátero mede sempre 60 graus.
A partir dessas características, nós podemos definir facilmente duas fórmulas importantes: a da altura e a da área de um triângulo equilátero com relação a medida do seu lado l. Começaremos pela altura, lembrando que ela deve ser sempre a medida do segmento que sai de um dos vértices do triângulo, e forma 90º com o lado oposto ao vértice escolhido, nesse caso, com a base do triângulo, como mostra a figura:
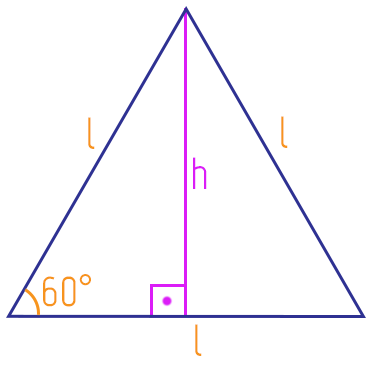
Se vocês repararem bem, o segmento formado pela altura do triângulo equilátero, que chamamos de h, acaba dividindo o triângulo pela metade. Vamos aproveitar essa ideia, e utilizar apenas uma das metades do triângulo para definirmos o valor exato da altura h. Tudo isso, porque assim obteremos um triângulo retângulo, e esta figura geométrica possui uma série de relações interessantes que poderemos utilizar.
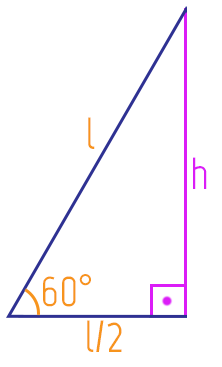
Nós estudamos no texto Relações Métricas no Triângulo Retângulo, que o maior lado de um triângulo retângulo é sempre a sua hipotenusa. Ainda, aprendemos que os demais lados, ou aqueles que formam um ângulo de 90º entre si, são os catetos do triângulo. Vejam então que o cateto h, é o cateto oposto ao ângulo de 60º que podemos ver na imagem. Assim, conhecendo as relações trigonométricas que podem ser aplicadas ao triângulo retângulo, no caso, o seno, o cosseno e a tangente, nós sabemos que aquela que está diretamente ligada ao cateto oposto h e a hipotenusa, que é o lado l do triângulo, é certamente o seno. Esse é o ponto de partida para definirmos a fórmula da altura do triângulo equilátero. Vejam só:

Bom, uma vez que conheçamos o valor do seno de 60º, poderemos obter uma relação entre a medida do lado do triângulo equilátero e a sua altura. Por isso vou deixar aqui a conhecida tabela dos ângulos notáveis, e a partir do valor apresentado nessa tabela, poderemos continuar nossa dedução.
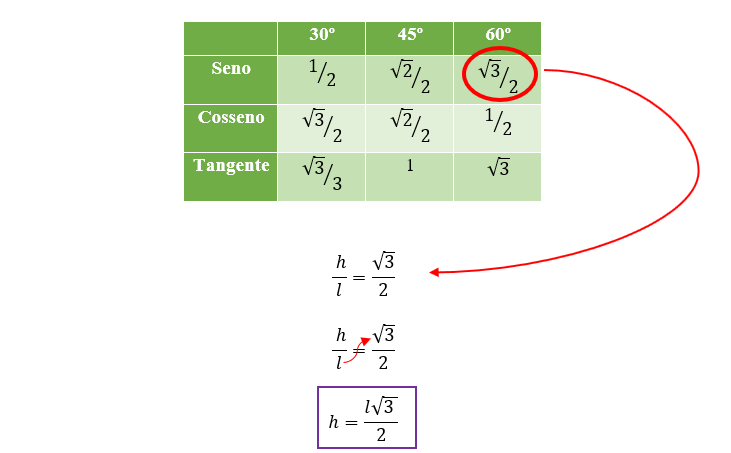
Fácil né!? Observem que para determinar a altura do triângulo equilátero, basta que multipliquemos a medida do lado desse triângulo por raiz quadrada de 3, e depois façamos a divisão do resultado por 2. Agora, vamos descobrir qual é a fórmula da área de um triângulo equilátero, e para isso, partiremos da fórmula utilizada para descobrir a área de todo e qualquer triângulo, a conhecida:
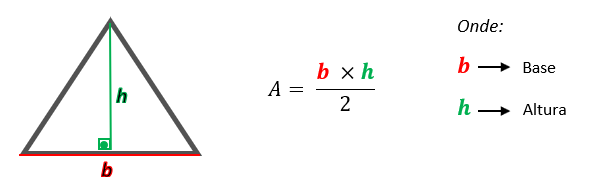
Comparando o triângulo que vemos na imagem acima, com o triângulo equilátero que estamos analisando, podemos perceber que o valor da base, no nosso caso, é l. Já com relação ao valor da altura, devemos lembrar que acabamos de deduzi-lo também em função de l. Substituindo todos os valores na fórmula, nós chegaremos a uma conclusão interessante, acompanhem!
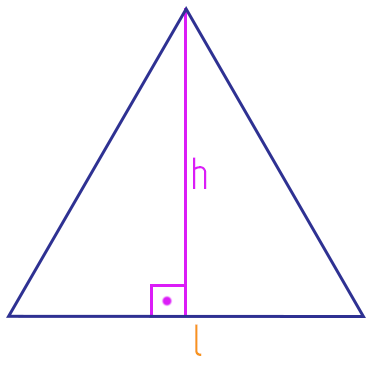
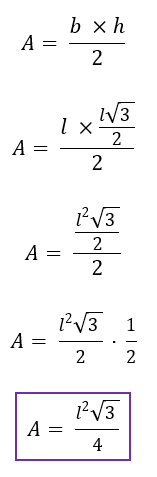
Chegamos a nossa tão esperada fórmula da área. Mas será que em meio a tantas fórmulas é possível memorizar mais uma? É claro que sim! Fiquem ligados na super dica que vou passar para vocês agora.

Vejam como a sequência de números 2, 3 e 4 pode nos ajudar a memorizar a fórmula. Basta dispor os números da maneira apresentada acima, e em seguida adicionar a letra l, a raiz quadrada e o sinal de divisão. Melhor agora não é? Assim nós podemos continuar, e veremos na sequência duas propriedades que envolvem os raios das circunferências inscrita e circunscrita ao triângulo equilátero. Vem comigo aqui!
1. PROPRIEDADES

1ª → Circunferência inscrita no triângulo equilátero e o seu apótema r
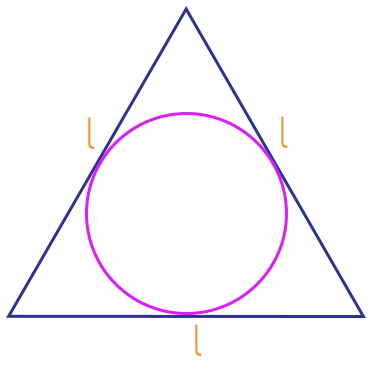
O apótema de um triângulo equilátero, nada mais é do que o raio da circunferência que está inscrita nele. Em outras palavras, podemos dizer que quando uma circunferência se encontra “dentro” de um triângulo equilátero, ela está inscrita nele, e nesse caso o seu raio será chamado de apótema, e será representado por r. A figura abaixo mostra mais detalhadamente o apótema de um triângulo equilátero.
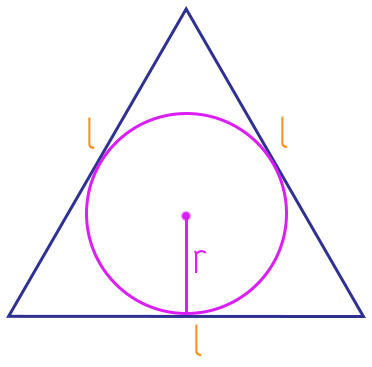
Acontece que, incrivelmente, se nós traçarmos o segmento que representa a altura do triângulo equilátero, veremos que o apótema r cabe 3 vezes nesse segmento, ou seja, a altura desse tipo de triângulo é sempre igual ao triplo de seu apótema, olhem só:
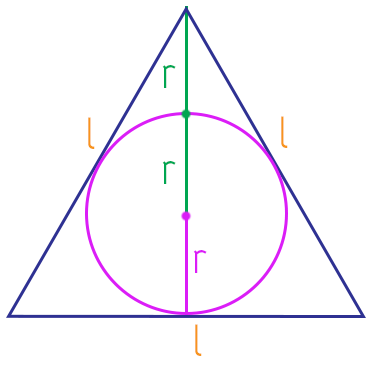
Assim, também podemos dizer que o apótema de qualquer triângulo equilátero é equivalente a 1/3 de sua altura.
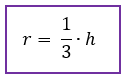
2ª → Circunferência circunscrita no triângulo equilátero e seu raio R
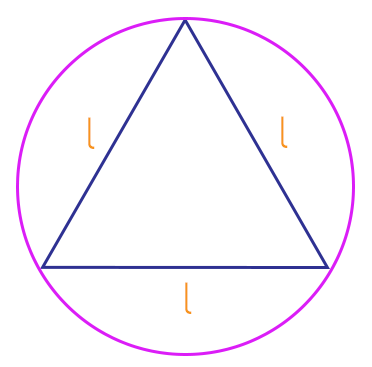
No caso em que a circunferência é circunscrita ao triângulo equilátero, ou seja, quando ela se encontra por fora desse triângulo, o seu raio não terá uma denominação específica, e será representado por R, porque claro, sempre será maior do que o apótema do triângulo equilátero. Vejam só como representa-lo:
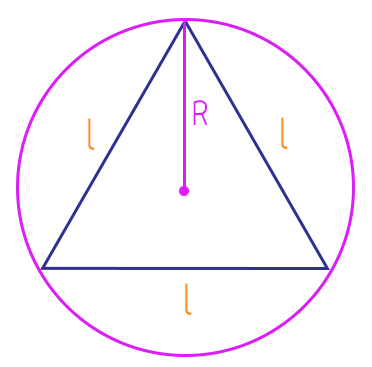
Aí novamente, se traçarmos o segmento que representa a altura do triângulo equilátero, e dividirmos o mesmo em três partes, veremos que o raio R da circunferência circunscrita ocupa duas dessas três partes que formam a altura, ou seja 2/3 da altura. Assim, podemos obter uma nova conclusão, olhem só!
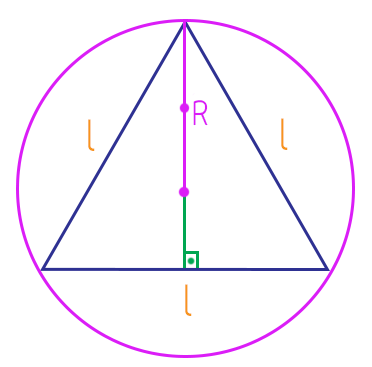
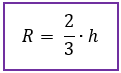
Comparando as duas fórmulas que acabamos de obter, vocês notaram algum detalhe interessante? Olhem bem, o apótema r, ou o raio da circunferência inscrita no triângulo equilátero equivale a 1/3 da altura do triângulo. Já o raio R, ou o raio da circunferência circunscrita no triângulo equilátero equivale a 2/3 da altura do mesmo triângulo. 2/3 não é exatamente o dobro de 1/3? Pois é, por isso podemos dizer também, que o raio R da circunferência circunscrita ao triângulo equilátero, é igual ao dobro do raio da circunferência inscrita nesse mesmo triângulo, ou seja, é igual ao dobro do apótema r.
![]()
Agora, para fixar tudo que aprendemos nesse texto, resolveremos um exercício bastante curioso. Vamos lá!
O lado, a altura e a área de um triângulo equilátero inscrito em um círculo formam, nessa ordem, uma progressão geométrica. Calcule o raio desse círculo.
Iniciaremos observando com cuidado todas as informações que o enunciado está nos passando. Vejam, primeiramente, que estamos falando de algumas características de um triângulo equilátero inscrito em um círculo. Ora, se o triângulo está inscrito em um círculo, significa que é ele que se encontra dentro da circunferência. Então o raio que se pede é aquele representado por R, ou seja, o raio da circunferência circunscrita ao triângulo equilátero.

Acontece que o lado, a altura e a área desse triângulo equilátero inscrito formam, nessa ordem, uma PG. Nós já estudamos no texto Definição e Classificação de uma Progressão Geométrica (PG), que uma progressão geométrica é uma sequência numérica que cresce ou decresce através do produto de seus termos por um valor constante, a razão da PG. Essa sequência pode ter quantos termos forem desejados, iniciando pelo primeiro termo, o a1, e seguindo com os demais termos a2, a3, a4, …, an. Assim, nós podemos dizer que o primeiro termo da sequência dessa questão é o lado l, o segundo termo é a altura h, e o terceiro termo é área do nosso triângulo inscrito na circunferência:
![]()
Antes de mais nada, é importante lembrarmos que nós definimos nesse texto, as fórmulas da altura e da área de um triângulo equilátero com relação ao seu lado l. Por isso, vamos realizar a substituição dessas fórmulas na sequência, e assim trabalharemos apenas com uma única incógnita.
![]()
Como foi dito agora a pouco, os termos de uma PG estão relacionados por uma razão, que chamamos de q. Essa razão pode ser obtida, quando dividimos um termo sucessor pelo seu antecessor, em qualquer ponto da sequência. Assim podemos dizer que:
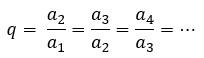
Se nós substituirmos os nossos termos em função do lado l, nas razões apresentadas acima, poderemos obter facilmente a medida do lado do triângulo equilátero, vejam só:
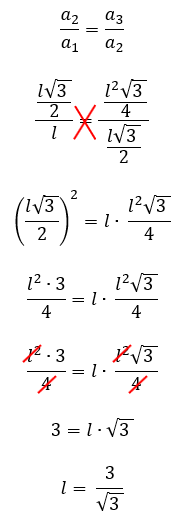
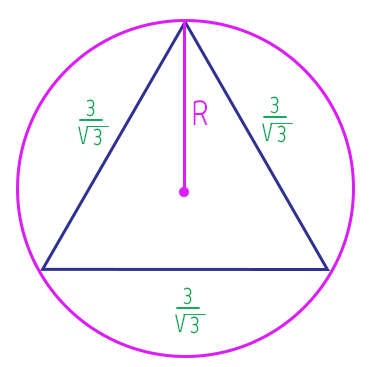
Finalmente descobrimos a medida do lado do nosso triângulo equilátero, mas lembrem-se que a questão nos pergunta o raio R da circunferência circunscrita. E agora? Simples, nós conhecemos a fórmula do raio R da circunferência circunscrita em função da altura do triângulo equilátero h. Mas conhecemos também a fórmula da altura do triângulo equilátero h em função da medida do seu lado l. E nós temos a medida do lado l. Pronto, basta realizar todas essas substituições!
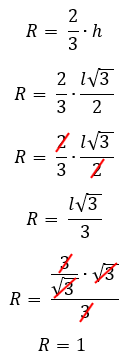
Percebam que a única complexidade que envolveu esse exercício, foi utilizar os conceitos de progressão geométrica para que fosse possível encontrarmos a medida do lado l do triângulo. No mais, apenas aplicamos boa parte das fórmulas que aprendemos hoje.
Por isso, ao finalizarmos mais um texto, eu espero que ele tenha sido muito proveitoso para os seus estudos, e ainda, que as dicas repassadas aqui possam ser utilizadas com facilidade, no momento oportuno. Deixo em anexo um vídeo, onde vocês encontrarão mais exercícios resolvidos, e claro, uma abordagem complementar do assunto.
Um abração! Nos vemos no próximo texto!