POLÍGONOS
06/03/2020
Os polígonos são figuras planas e fechadas constituídas por segmentos de reta que não se cruzam, a não ser em suas extremidades. Também é possível definir um polígono como qualquer figura plana formada pelo mesmo número de ângulos e lados.
Olá, pessoal! Tudo certo por aí?
Os polígonos são figuras geométricas que compõem a base da geometria plana. Por isso, vamos estudar aqui a classificação dos polígonos, os seus elementos e a nomenclatura dos polígonos de acordo com o número de lados. Além disso, vamos conhecer uma série de fórmulas que relacionam os ângulos, os lados e as diagonais de um polígono. Se você é um amante da geometria plana, ou precisa desvendá-la para se dar bem nas provas do ENEM e dos vestibulares, não deixe de acompanhar o texto comigo!
Tranquilo, pessoal? Então, como é de costume: vem comigo aqui!
1. O QUE É UM POLÍGONO?
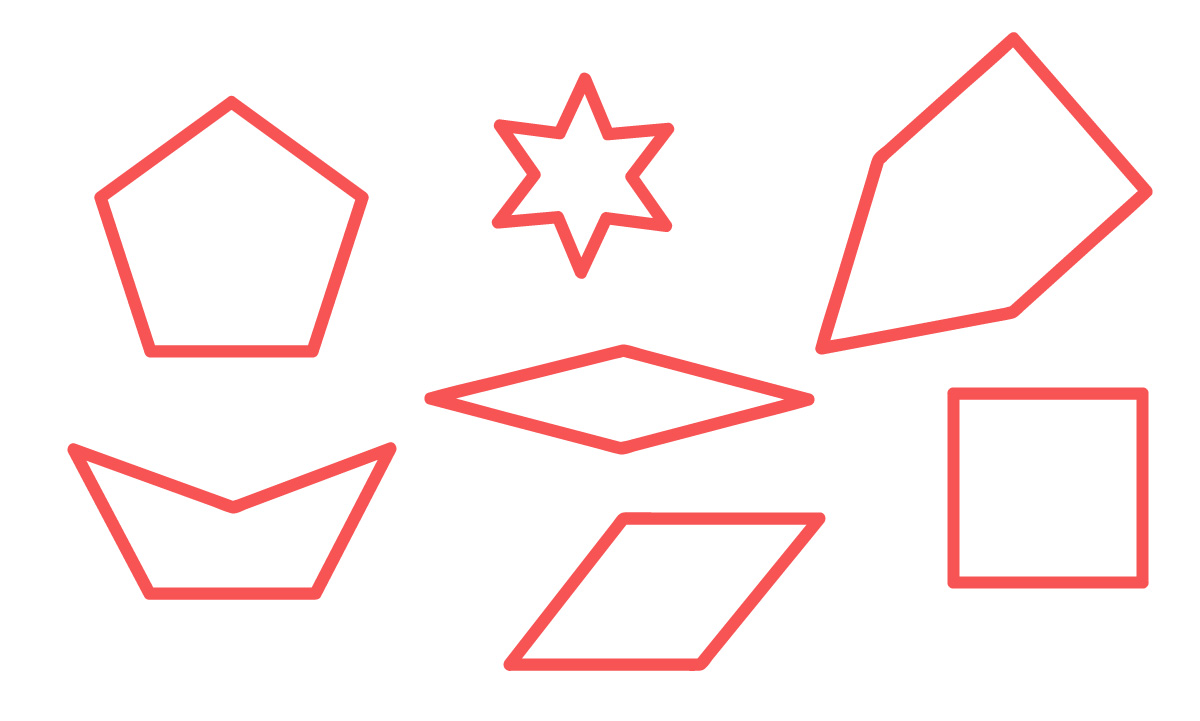
Os polígonos são figuras planas e fechadas constituídas por segmentos de reta que não se cruzam, a não ser em suas extremidades. Apesar dessa definição soar um tanto confusa, quando nos deparamos com figuras geométricas que não são polígonos, fica um pouco mais simples compreender o seu real significado. Olhem só!
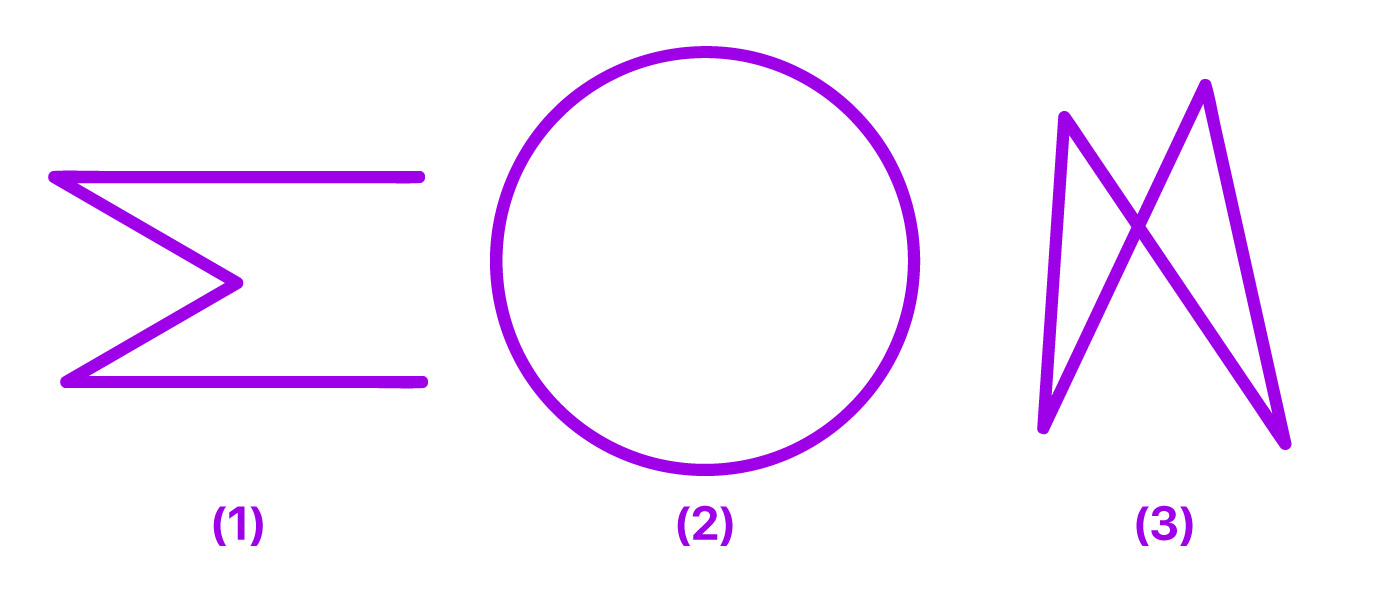
Na imagem acima, vemos 3 figuras que não são polígonos. A primeira delas não é um polígono porque não é fechada. A segunda, não é um polígono porque não é constituída por segmentos de reta. A terceira, também não pode ser um polígono, pois apesar de ser formada por segmentos de reta, estes segmentos se cruzam ao formar a figura.
Incrível, não é? Bom, agora que conhecemos a definição de polígono, estamos prontos para entender a sua classificação. Sigam comigo!
2. TIPOS DE POLÍGONOS
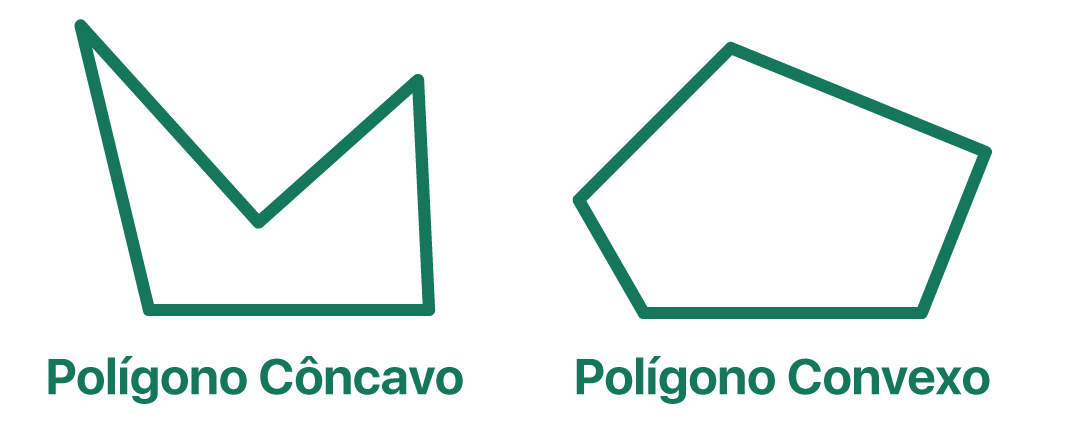
Os polígonos costumam ser classificados como côncavos ou convexos. Vocês podem identificar quando um polígono é côncavo e quando é convexo traçando um segmento de reta sobre a figura. Feito isso, é possível tirar as seguintes conclusões:
2.1 Polígono Côncavo

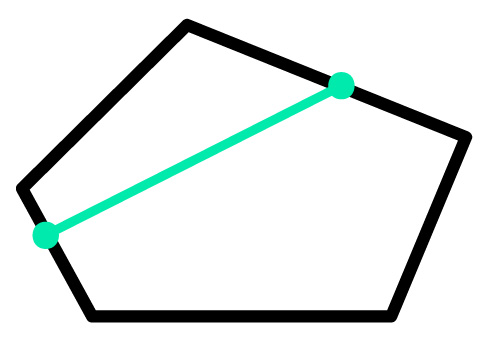
Um polígono é considerado côncavo, quando a reta consegue interceptá-lo em mais de dois pontos. Também é possível identificar que um polígono é côncavo, quando o segmento de reta traçado não pertence somente à região limitada pelo polígono, ou seja, quando uma parte dele está pra fora dos limites do polígono.

Para memorizar o nome deste polígono, lembrem que côncavo é sinônimo de concavidade, buraco, depressão (geog.). Assim, um polígono côncavo é aquele que possui um “buraco”.
2.2 Polígono Convexo
Um polígono é considerado convexo, quando a reta consegue interceptá-lo no máximo em dois pontos. Também é possível identificar que um polígono é convexo, quando o segmento de reta traçado pertence somente à região limitada pelo polígono, como mostra a imagem abaixo.
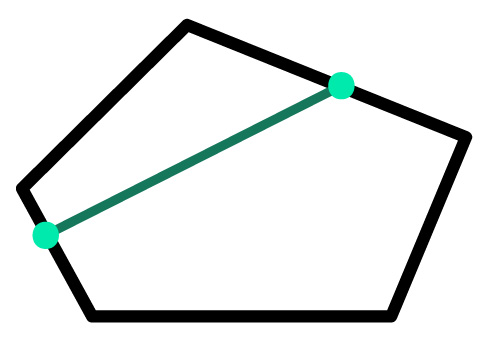
E aí, ficou clara a diferença entre os polígonos? A partir desse momento, nós vamos voltar nossos estudos apenas para o polígono convexo. Vem comigo!
3. ELEMENTOS DE UM POLÍGONO
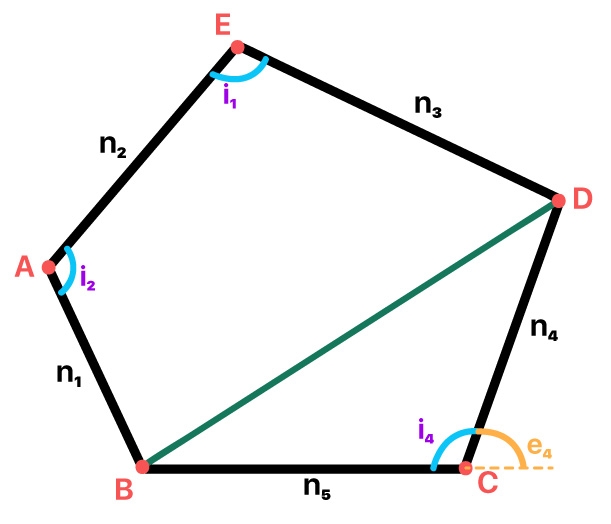
Todo polígono possui um certo número de lados, de vértices, de diagonais e de ângulos internos e externos. Conhecer cada um desses elementos nos permite estabelecer algumas fórmulas bem importantes para o estudo dos polígonos. É isso que faremos na sequência, acompanhem!
3.1 Lados
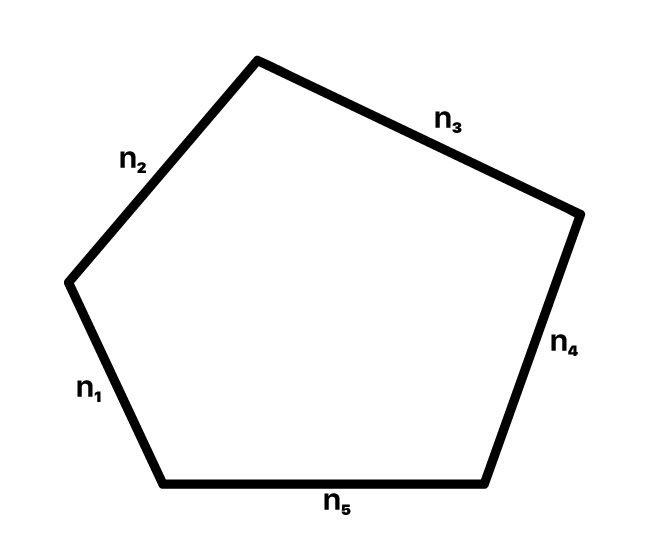
Os lados são os segmentos de reta que formam o polígono. Geralmente, os lados são identificados pela letra n.
3.2 Vértices
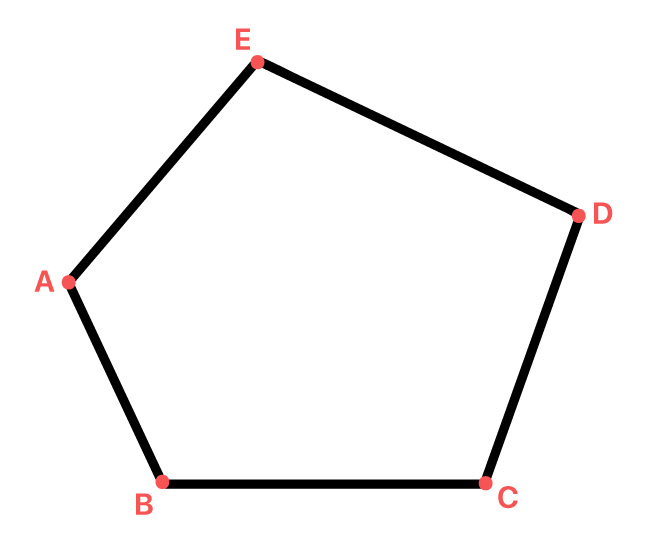
Os vértices são os pontos de encontro entre dois lados consecutivos (sucessivos) de um polígono. Geralmente, identificamos os vértices por letras maiúsculas do alfabeto.
3.3 Diagonais
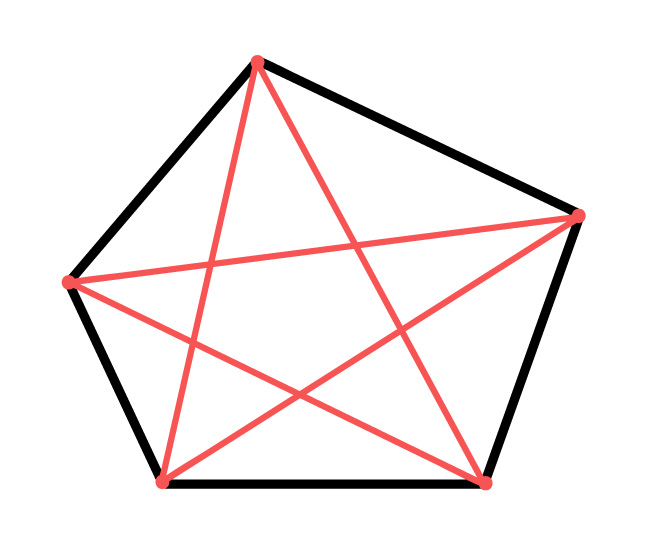
As diagonais de um polígono são segmentos de reta cujas extremidades são vértices não consecutivos do polígono. Isso porque, quando unimos dois vértices consecutivos de um polígono, na verdade, formamos um de seus lados.
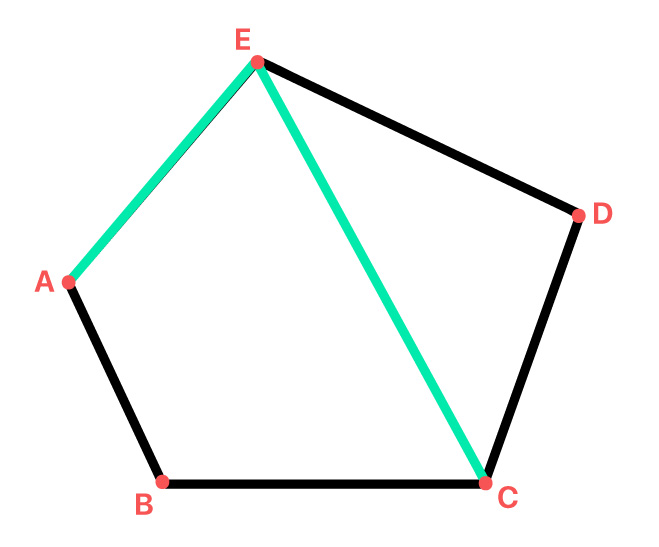
Reparem na imagem acima, que as extremidades do segmento 



No quadro acima, vemos uma fórmula muito conhecida que permite determinar o número de diagonais d de um polígono em função do número de lados n. Anotem esta fórmula, afinal, ela será muito útil na resolução de exercícios que envolvem os polígonos!
CURIOSIDADE

O pentágono é o único polígono cujo número de diagonais é exatamente igual ao número de lados. Para comprovarmos tal afirmação, vamos substituir o n da fórmula que acabamos de conhecer por 5 e verificar qual será o número de diagonais encontrado.
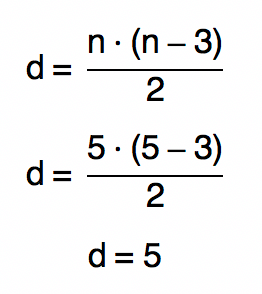
3.4 Ângulos Internos e Externos
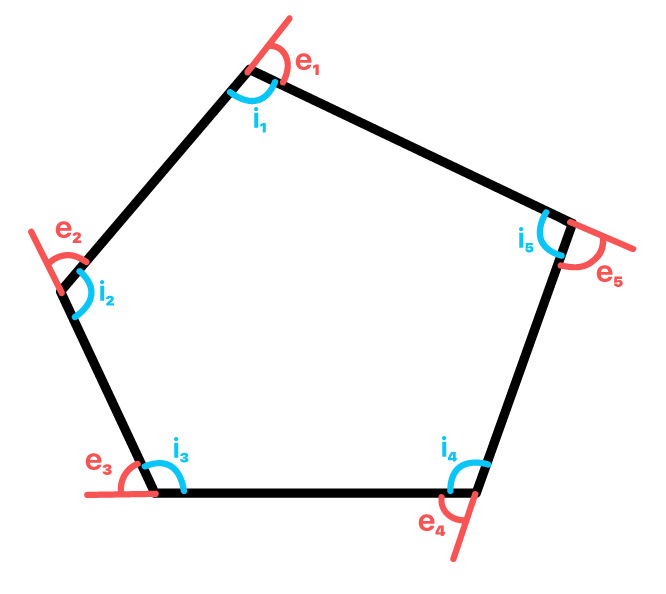
Todo polígono possui ângulos internos, que se formam entre dois de seus lados consecutivos. Além disso, os polígonos possuem ângulos externos, formados entre um lado do polígono e o prolongamento do lado consecutivo a este. Na imagem acima, podemos observar os ângulos internos (i1, i2, i3, i4, i5) e externos (e1, e2, e3, e4, e5) de um polígono de 5 lados.
A imagem não deixa dúvidas de que todo ângulo interno possui um ângulo externo correspondente. Tanto é verdade, que se repararmos melhor no polígono apresentado, veremos que cada ângulo interno forma junto com seu respectivo ângulo externo um ângulo raso, ou seja, de 180º. Isso significa que em qualquer polígono, todo ângulo interno é suplementar ao seu respectivo ângulo externo.
i + e = 180º
Além da relação acima, é muito importante que vocês dominem a soma dos ângulos internos (Si) e externos (Se) dos polígonos. A soma dos ângulos externos de qualquer polígono é sempre 360º, independente do formato ou de qualquer outra característica do polígono. Enquanto isso, a soma dos ângulos internos depende do número n de lados do polígono, e pode ser calculada através da seguinte fórmula:

Entendido, pessoal? Anotem estas fórmulas aí porque vamos utilizá-las em breve! Agora, vamos conhecer a nomenclatura dos polígonos de acordo com o número de lados que eles apresentam. Vem comigo!
4. NOMENCLATURA DOS POLÍGONOS

Legal, não é, pessoal? Salvem essa tabela para não esquecer mais a nomenclatura dos polígonos!
E agora, depois de todo esse conhecimento, nada mais justo do que resolvermos alguns exercícios para consolidar o aprendizado. Sigam comigo até o próximo item!
5. EXERCÍCIOS RESOLVIDOS SOBRE OS POLÍGONOS

Exercício 1
Determine o polígono cujo número de diagonais é o quádruplo do número de lados.
Conforme informa o exercício, o número de diagonais “d” do polígono em questão é 4 vezes maior que o número de lados “n”, ou seja, d = 4n. Portanto, podemos utilizar a fórmula do número de diagonais do polígono, e substituir o valor de “d” por “4n”. Isso nos permitirá encontrar o número de lados do polígono, que consequentemente, nos levará a sua nomenclatura. Acompanhem comigo!
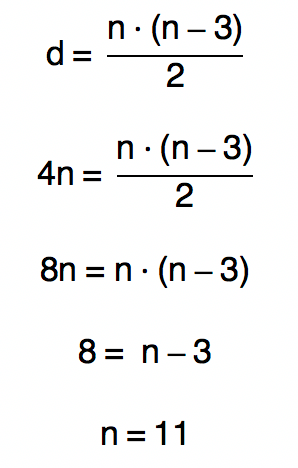
Assim como mostra a tabela que observamos logo acima, um polígono de 11 lados é um undecágono.
Exercício 2
Qual é o polígono em que a soma das medidas dos ângulos internos é o quadruplo da soma das medidas dos ângulos externos?
Em forma de equação, podemos transcrever o enunciado da seguinte forma:
Si = 4 . Se
Sabemos que a soma dos ângulos externos de um polígono é sempre 360° e que a soma dos ângulos internos é dada pela fórmula “Si = 180º ⋅ (n – 2)”. Assim, podemos substituir esses dois valores na equação acima:
Si = 4 . Se
180º ⋅ (n – 2) = 4 . 360º
n – 2 = 4 . 2
n = 8 + 2
n = 10
Dessa forma, como são 10 lados, o polígono procurado se chama decágono.
Exercício 3
Em um polígono, a soma dos ângulos internos e externos é 1080º. Determine o seu número de diagonais.
Novamente, de acordo com enunciado, podemos estabelecer a seguinte equação:
Si + Se = 1080º
Substituindo o termo Si por “180º ⋅ (n – 2)” e o termo Se por “360º”, podemos encontrar o número de lados do polígono descrito no exercício.
Si + Se = 1080º
180º ⋅ (n – 2) + 360º = 1080º
180º ⋅ (n – 2) = 1080º – 360º
180º ⋅ (n – 2) = 720º
n – 2 = 4
n = 6
Acontece que nesse caso, não é o número de lados que está sendo requisitado, mas sim, o número de diagonais do polígono. Por isso, vamos encontrar esse número com a fórmula do número de diagonais que também aprendemos aqui.
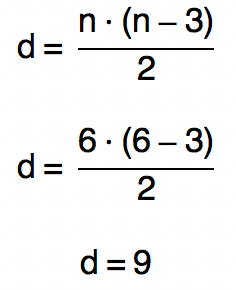
Entendido, pessoal? Caso tenha restado alguma dúvida sobre as equações e fórmulas que utilizamos nos exercícios, acompanhem o vídeo disponível logo abaixo. Nele eu resolvo outros exercícios também, e dou uma pincelada na teoria para vocês ficarem craques no assunto.
Gostou desse conteúdo? Clique aqui para saber como a Plataforma do Professor Ferretto funciona!
Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!
Assim, é chegada a hora de concluirmos o texto! Espero que este assunto tenha sido muito proveitoso para os estudos de vocês!
Um abraço, sucesso e até mais!