A racionalização de denominadores é um processo utilizado para eliminar os radicais dos denominadores das frações sem alterar o valor inicial das frações como um todo. Ao racionalizar um denominador, transformamos o seu valor irracional em um valor racional.

 

Olá, pessoal! Tudo bem?

Hoje nós iremos estudar um assunto da matemática básica que é muito intrigante, sob diversos pontos de vista: a racionalização de denominadores! Vamos aprender aqui como racionalizar um denominador, e também o que significa “racionalizar” um denominador. Além disso, tenho certeza que muitos de vocês já se perguntaram: é mesmo necessário efetuar a racionalização? Pois bem, o texto de hoje visa esclarecer todas essas dúvidas, e proporcionar a vocês um aprendizado completo deste assunto!

Beleza, pessoal? Então, vamos aos estudos! Vem comigo!

 

1. O QUE SIGNIFICA RACIONALIZAR UM DENOMINADOR?

É verdade que a gente costuma ouvir a expressão “racionalização de denominadores” e já pensa em algo como “eliminar ou remover” a raiz do denominador de uma fração. É claro que isso não está errado, mas então, por que será que o nome dessa operação não é simplesmente esse “Eliminar a raiz de um denominador”?

No esquema acima, nós vemos duas frações equivalentes, ou seja, frações cujo valor decimal é exatamente o mesmo, e neste caso, igual a 0,707…. Antes de sofrer o processo de racionalização, o denominador da fração era composto por uma raiz não exata, que é considerada um número irracional. Contudo, após haver a racionalização deste denominador, o seu valor passou a ser um número racional. Isso nos mostra que racionalizar um denominador significa transformar o seu valor irracional em um número racional.

 

ATENÇÃO A RACIONALIZAÇÃO DE DENOMINADORES

O processo de racionalização de denominadores transforma o denominador irracional de uma fração em um número racional, mas não transforma a fração como um todo em um número racional. É por isso que falamos sempre em “Racionalização de Denominadores” e não em “Racionalização de Frações”.

 

2. POR QUE DEVEMOS RACIONALIZAR O DENOMINADOR DE UMA FRAÇÃO?

A racionalização de denominadores surgiu num período em que não contávamos com as calculadoras científicas e gráficas que conhecemos hoje. Naquela época, a maioria dos cálculos, incluindo as divisões, era feita de forma manual. Desta maneira, era muito mais simples trabalhar com raízes não exatas no numerador de uma fração, do que no seu denominador. Mesmo hoje, realizar cálculos com raízes no denominador pode ser um problema para as calculadoras mais simples, devido a ordem em que as operações são realizadas por elas.

Mas matematicamente falando, e, com os recursos atuais, é claro que não faz diferença racionalizar ou não um denominador. Muitos autores apelam para a estética da fração, e afirmam que ela fica mais “bonita” quando o denominador é racionalizado. Contudo, isso é apenas uma questão de preferência! Nenhum resultado fracionário pode ser considerado errado porque o seu denominador não foi racionalizado.

Bom, agora que já descobrimos uma série de informações importantes sobre o processo de racionalização de denominadores, vamos aprender como fazer isto de fato. Sigam comigo até o próximo item!

 

3. COMO RACIONALIZAR UM DENOMINADOR?

Nos próximos itens, nós vamos aprender a racionalizar 3 tipos de denominadores. Mas para que o método utilizado nos três casos fique bem claro para todos vocês, antes disso, vamos dar uma breve revisada em um conceito muito importante para a matemática. Vem comigo!

 

3.1 Elemento neutro da multiplicação

De forma simplificada, todo elemento é neutro quando sua utilização em uma operação matemática não causa alteração no outro elemento com o qual este entra em operação. E aí eu pergunto para vocês: qual é o único valor numérico que quando multiplicado por qualquer outro número real, não altera o valor deste número?

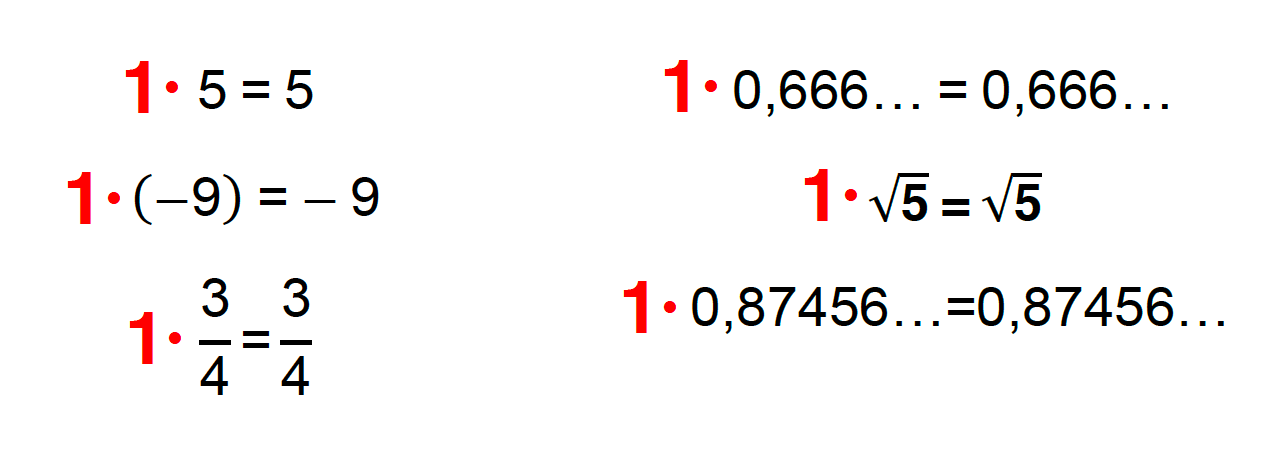
É isso mesmo! Sempre que multiplicamos um número real por 1, não causamos alteração alguma nesse número real. Pensando nisso, tentem responder a mais uma pergunta: qual é o resultado da divisão de qualquer número real por ele mesmo?

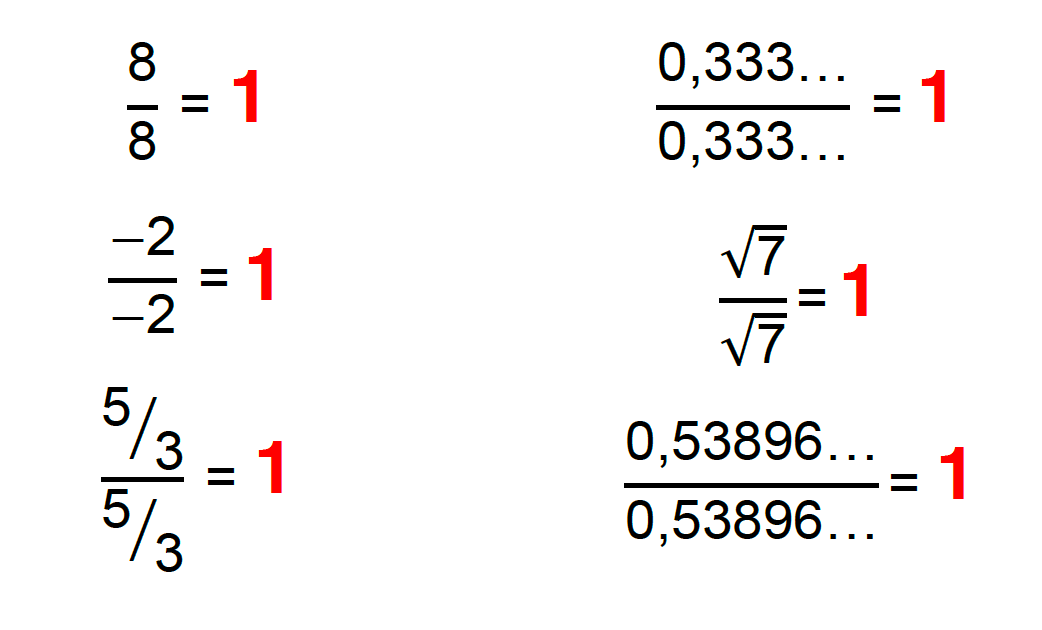
A partir destes dois argumentos, é possível concluir que ao multiplicarmos qualquer número real por uma fração cujo numerador e denominador possuem o mesmo valor, não alteramos este número real inicial. É como se estivéssemos multiplicando esse número por 1, e multiplicar qualquer número por 1 não causa alterações em seu valor inicial!

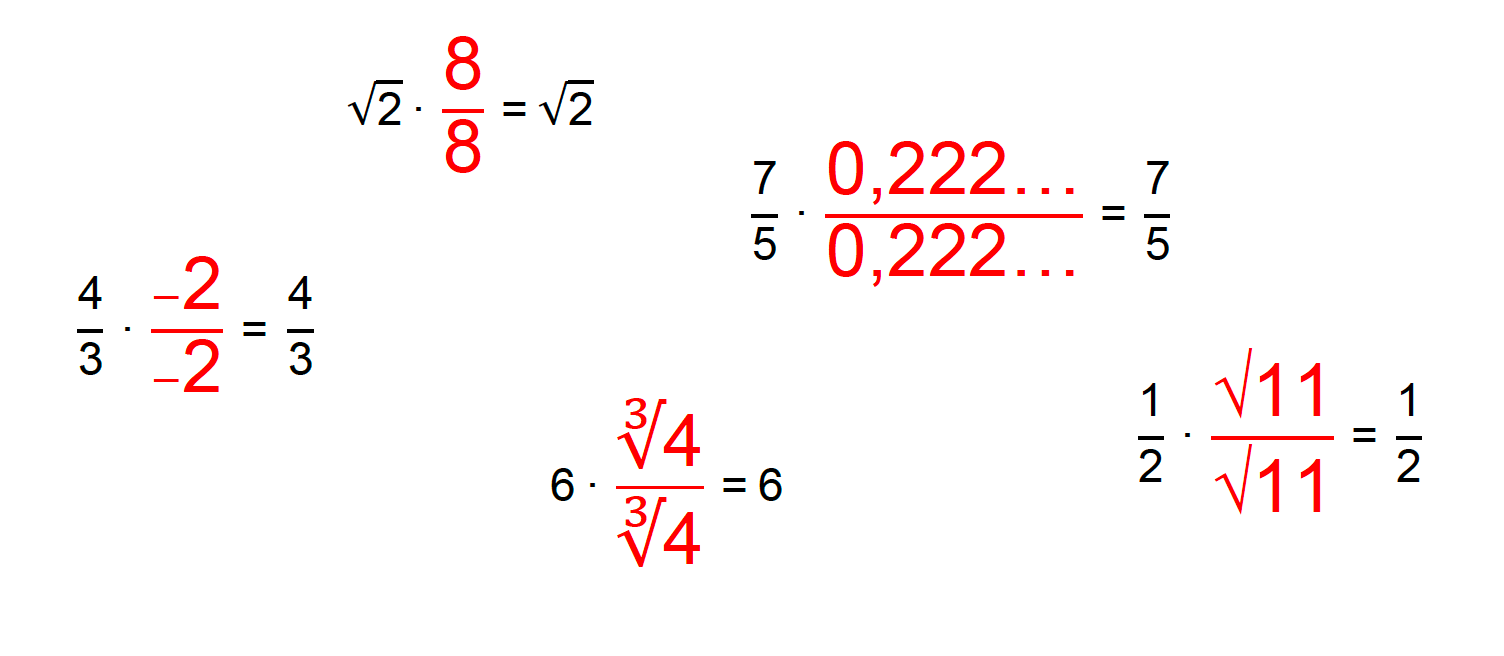
A racionalização de denominadores é um processo que consiste em transformar o denominador irracional de uma fração em um número racional, sem alterar o valor inicial da fração como um todo, não é mesmo? Por isso estudamos o elemento neutro da multiplicação. Para racionalizar os denominadores, nós vamos multiplicar o numerador e o denominador das frações por um mesmo número, que chamamos de fator racionalizante. Acompanhem comigo qual será o fator racionalizante de cada um dos 3 casos que vamos estudar.

 

3.2 Quando o denominador é um radical de índice 2

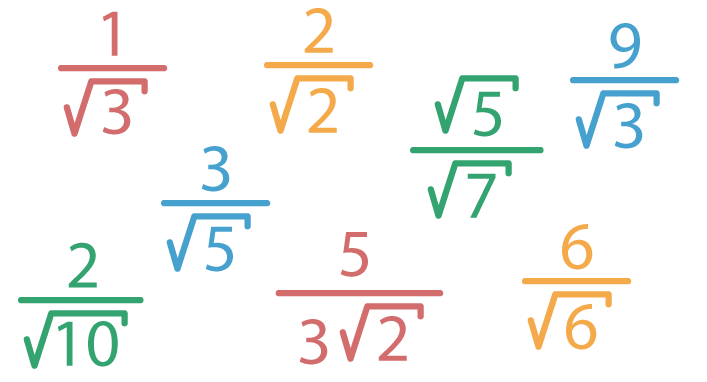
Quando o denominador de uma fração é composto por uma única raiz quadrada, ou seja, por um radical índice 2, tem-se o caso mais simples de racionalização. Isso porque, para eliminar um radical de índice dois, basta multiplica-lo por ele mesmo, como mostra o seguinte exemplo algébrico.

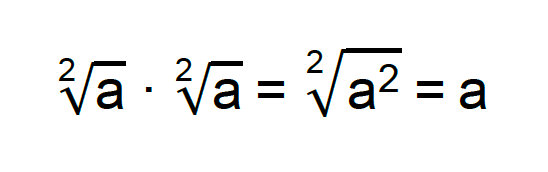
Assim, é possível concluir que o fator racionalizante, ou o fator que elimina um radical de índice 2 é ele próprio!

 

3.3 Quando o denominador é um radical de índice maior do que 2

Quando o denominador de uma fração é composto por um radical de índice maior do que 2, ou seja, uma raiz cúbica, quarta, quinta e por aí vai, o processo de racionalização se torna um pouquinho mais complicado. Isso porque, para eliminar um radical de índice maior do que dois, não basta multiplicá-lo por ele mesmo, como mostra o seguinte exemplo algébrico de uma raiz cúbica.

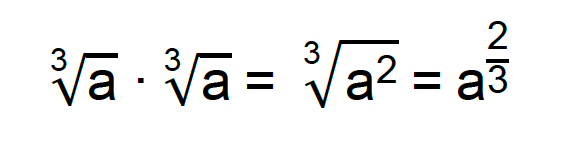
Vejam que não foi possível eliminar o radical do exemplo, porque o expoente de a, 2, não era igual ao valor do índice da raiz, 3. Por isso, quando o denominador de uma fração possui um único radical de índice maior que 2, o fator racionalizante é também um radical de mesmo índice, mas com uma pequena mudança no expoente do radicando a. Este expoente deve ser um valor que quando somado ao expoente do radicando original, resulte no índice da raiz. O quadro abaixo retrata essa ideia.

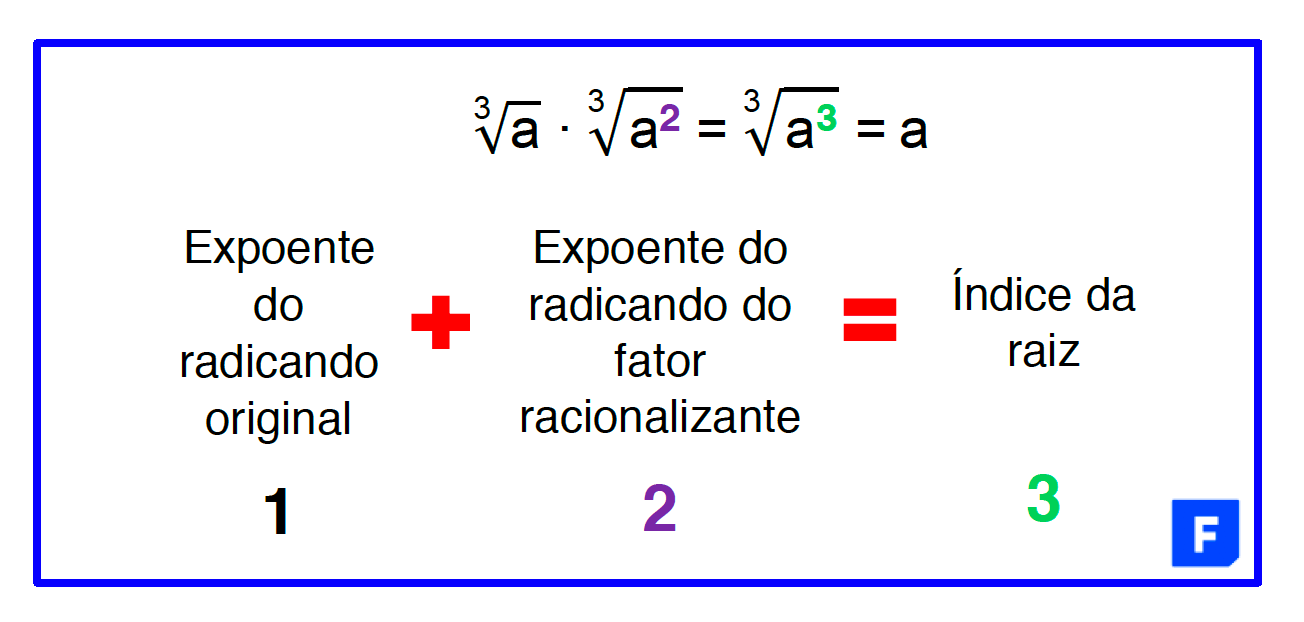
Assim, para ficar bem fácil de descobrir o fator racionalizante correto deste tipo de denominador, vocês podem seguir os seguintes passos:

1° Passo: Observem qual é o índice da raiz e qual é o expoente do radicando.

2° Passo: Façam a seguinte pergunta: quanto falta do expoente do radicando para o índice da raiz? A resposta dessa pergunta é o valor do expoente do radicando do fator racionalizante!

Ficou claro, pessoal? Após estudarmos o próximo caso de racionalização de denominadores, vamos praticar essas ideias com exemplos. Vem comigo aqui!

 

3.4 Quando o denominador é do tipo √a ± √b

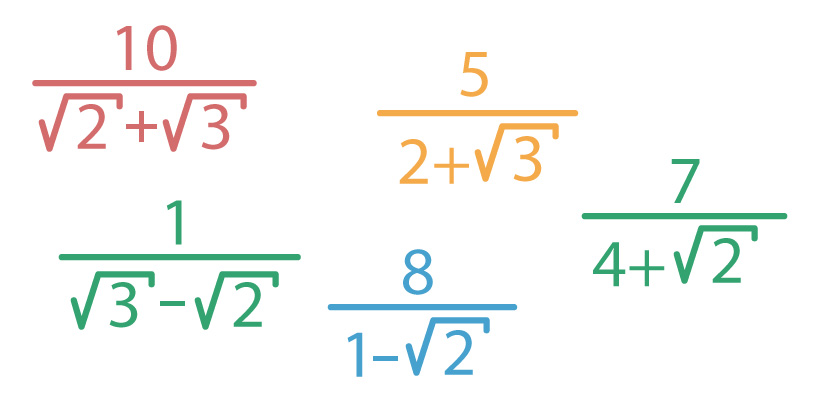
Quando o denominador de uma fração é composto pela soma ou diferença de dois radicais de índice 2, ou ainda, pela soma ou diferença entre um radical de índice 2 e um número inteiro, encontramos o fator racionalizante através do produto notável conhecido como “produto da soma pela diferença”.

(a + b) ∙ (a – b) = a² – b²

Vejam que o resultado deste produto notável é dado pela diferença entre dois termos elevados ao quadrado. Isso é ótimo, afinal, quando um radical de índice dois é elevado ao quadrado, ele é eliminado!

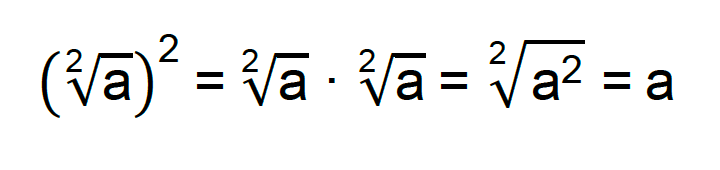
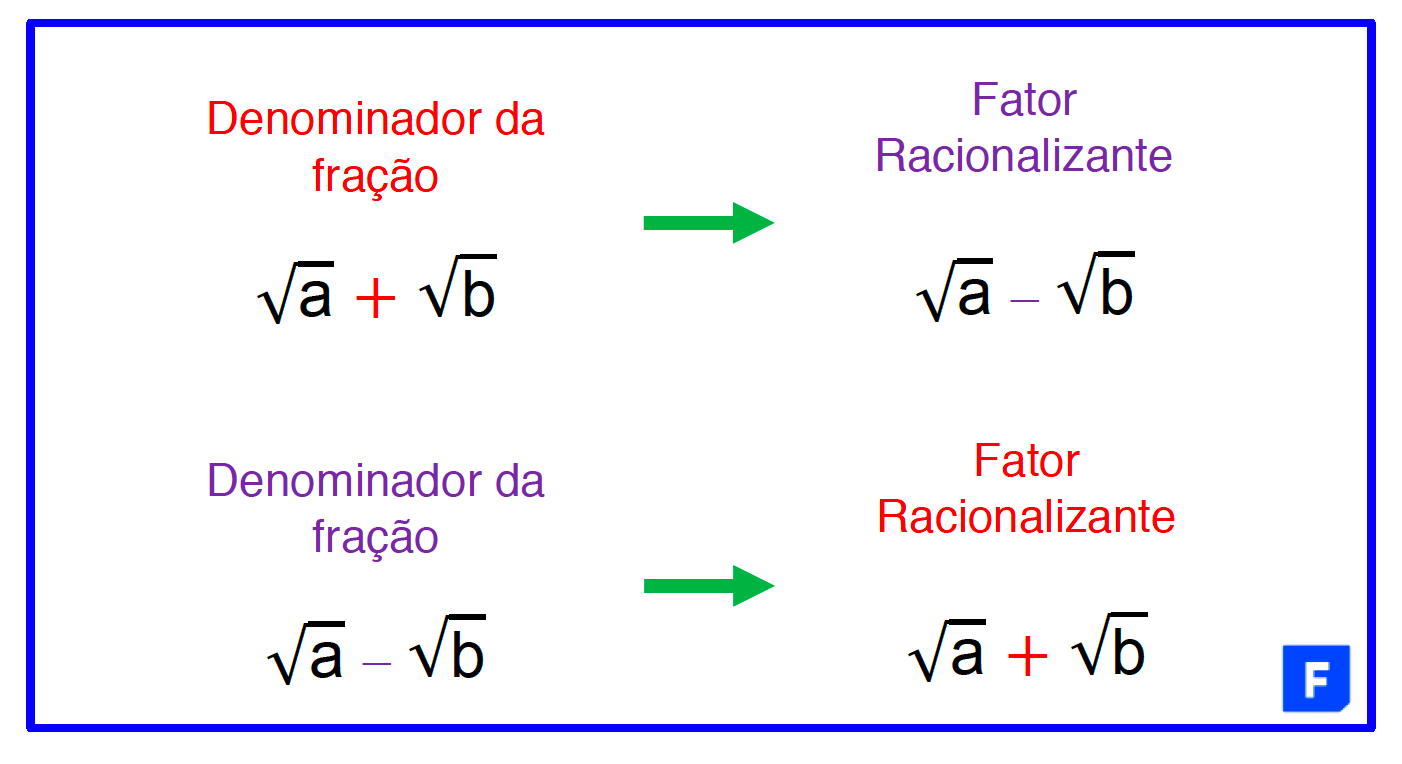
Portanto, pessoal, para encontrar o fator racionalizante deste tipo de denominador, basta ficar atento ao a operação que está sendo realizada entre os radicais. Se houver uma soma de dois radicais, o fator racionalizante será a diferença entre os mesmos radicais, mas se houver uma diferença entre dois radicais, claro, o fator racionalizante será a soma entre esses mesmos radicais. O quadro abaixo retrata essa ideia.

Entendido? Então, vamos aplicar todo o conhecimento adquirido até aqui. Sigam comigo!

 

4. EXEMPLOS DE RACIONALIZAÇÃO DE DENOMINADORES

A partir de agora, nós vamos racionalizar uma série de denominadores. Em todos os exemplos, analisaremos em qual dos casos estudados a fração se encaixa, determinaremos o fator racionalizante, e na sequência, multiplicaremos numerador e denominador da fração pelo fator determinado. Acompanhem comigo!

 

Exemplo 1

Racionalize o denominador da seguinte fração:

1/√3

Fator racionalizante: √3

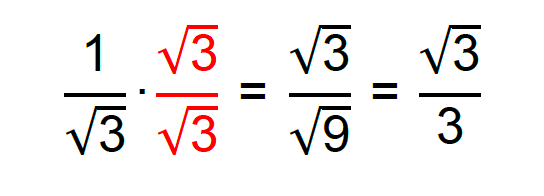
Para provar que o método dá certo, vemos abaixo que as frações 1/√3 e √3/3 são equivalentes:

 

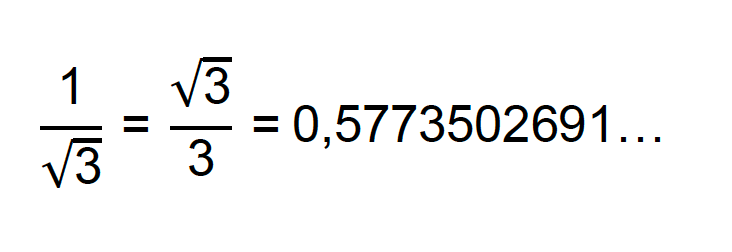
Exemplo 2

Racionalize o denominador da seguinte fração:

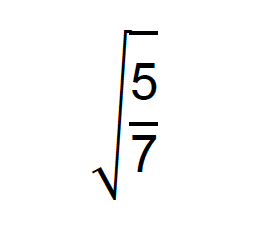
Neste caso, pessoal, é muito importante prestar atenção no seguinte detalhe. Por mais que a fração inteira esteja dentro do radical, existe uma propriedade da radiciação que nos permite reescrevê-la com o mesmo radical no numerador e no denominador. Desta forma, podemos determinar o fator racionalizante e seguir com a resolução do caso.

Fator racionalizante: √7

 

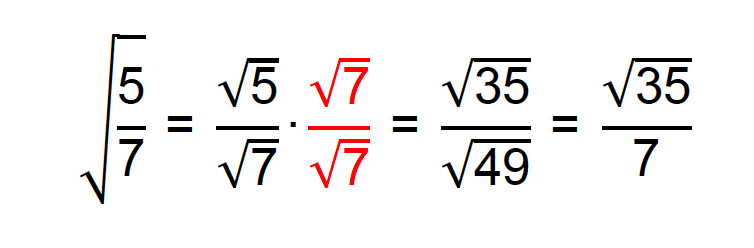
Exemplo 3

Racionalize o denominador da seguinte fração: 

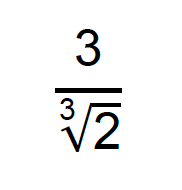
O radical do denominador dessa fração é uma raiz cúbica, ou seja temos um índice igual a 3. Enquanto isso, o expoente do radicando 2, é de valor 1(reparem que não está aparecendo!). Aí vem a pergunta: quanto falta de 1 para 3? 3 – 1 = 2!

Fator racionalizante: ∛2² 

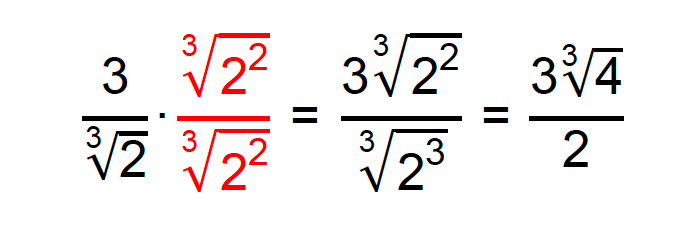
Novamente, temos a comprovação de que a fração inicial e a fração já racionalizada são equivalentes:

 

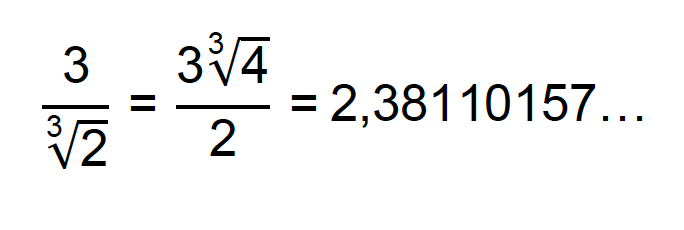
Exemplo 4

Racionalize o denominador da seguinte fração:

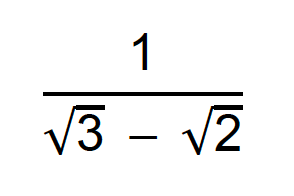
Observem que o denominador desta fração é composto por uma diferença entre dois radicais. Assim, o fator racionalizante deste exemplo deve ser a soma desses mesmos radicais.

Fator racionalizante: √3 + √2

 

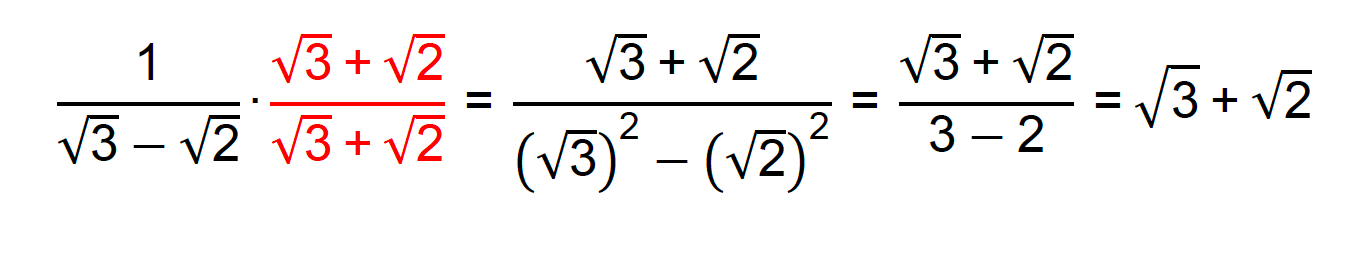
IMPORTANTE

As vezes, por pura falta de atenção ou descuido, podemos somar radicais que não são semelhantes. Então fica a dica, pessoal! Não é possível somar radicais que não são semelhantes! Se vocês encontrarem um resultado tal como o do exemplo que acabamos de resolver, mantenham-o como está.

√3 + √2 = √5 

√3 + √2 = √3 + √2 

√3 + √3 = 2√3 

 

Exemplo 5

Racionalize o denominador da seguinte fração:

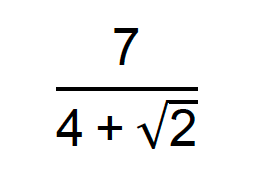
Como estudamos neste texto, também podemos racionalizar denominadores compostos pela soma ou diferença entre um radical e um número inteiro. Da mesma forma que no exemplo anterior, basta lembrar do produto notável conhecido como “produto da soma pela diferença”. Se temos uma soma entre os dois termos do denominador da fração, o fator racionalizante será composto pela diferença entre esses mesmos dois termos.

Fator racionalizante: 4 – √2 

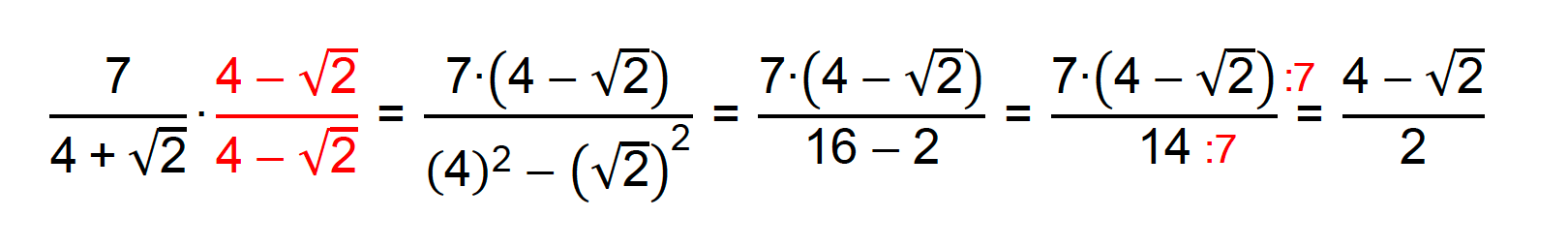
Entendido, pessoal? Sendo assim, é hora de encerrarmos este texto! Espero ter atingido nosso objetivo inicial, que era esclarecer todas as dúvidas de vocês, e com isso, tornar seus estudos muito mais proveitosos! Em anexo disponibilizo um vídeo, com o qual vocês poderão complementar todo o conhecimento visto por aqui.

Gostou desse conteúdo? Clique aqui para saber como a Plataforma do Professor Ferretto funciona!

Deseja ter uma preparação completa em matemática e ciências da natureza? Então você precisa conhecer os planos e cursos da plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!

Um abração e até mais!