Talvez você já tenha se questionado sobre quem ensina cada disciplina nas plataformas de cursinho online para o Enem. Por...
Dízima Periódica: o que é, classificação e a Fração Geratriz
A dízima periódica é um número decimal não exato que pode ser representado na forma de fração. Estude tudo sobre a dízima periódica e a sua fração geratriz aqui!
Ferramentas de IA
Sugestões personalizadas
Uma dízima periódica é um número decimal cujas casas decimais são compostas por grupos de um ou mais algarismos que se repetem infinitamente, ou seja, que são periódicos. As dízimas periódicas podem ser escritas na forma de fração, por isso, elas pertencem ao conjunto dos números racionais (ℚ).
Olá, pessoal! Tudo bem?
A dízima periódica é um número racional muito importante para a matemática básica. Por isso, vamos dedicar este texto inteirinho a ela!
Estudaremos o conceito de dízima periódica, sua classificação, e claro, como encontrar a fração geratriz de qualquer dízima, seja ela simples ou composta.
Ao final, vamos resolver uma série de exemplos, e assim, vocês estarão preparados para encarar o assunto nas provas do ENEM, de vestibulares e até mesmo de concursos públicos!
Certo, pessoal? Dessa forma, é hora de desvendarmos os mistérios das dízimas periódicas. Vem comigo!
O que é dízima periódica?
Assim como vimos no primeiro parágrafo deste texto, uma dízima periódica é um número decimal não exato cujas casas decimais são compostas por grupos de um ou mais algarismos que se repetem infinitamente.
Reparem no quadro acima, que todos os números apresentados possuem algarismos que se repetem infinitamente. Esses algarismos formam o período da dízima periódica.
1,3592929292 … → Período: 92
0,33333 … → Período: 3
2,66666 … → Período: 6
0,285714285714 … → Período: 285714
1,21616161616 … → Período: 16
0,00777777 … → Período: 7
Contudo, nem sempre as casas decimais de uma dízima periódica são compostas apenas por seu período. Às vezes, aparecem alguns números intrusos entre a vírgula e o período de um decimal periódico. Intrusos!? Exatamente.
O grupo de um ou mais números que não se repete, e que pode aparecer em uma dízima periódica antes da formação de seu período, costuma ser chamado de intruso, ou de antiperíodo.
Alguns dos números que temos analisado possuem algarismos intrusos, confiram aí!
1,3592929292 … → Intruso: 35
0,33333 …
2,66666 …
0,285714285714 …
1,21616161616 … → Intruso: 2
0,00777777 … → Intruso: 00
É justamente a presença ou não de algarismos intrusos ou de um antiperíodo em uma dízima periódica que dá origem a sua classificação.
Vamos estudar essa classificação com detalhes depois de um alerta bem importante. Vem comigo!
Quando um decimal não é uma dízima periódica
Quando os algarismos infinitos de um número decimal não exato não possuem nenhum padrão, ou seja, não possuem período, eles não são dízimas periódicas.
Neste caso, estamos diante de números irracionais, como os seguintes exemplos:
√2 = 1,414213562…
√3 = 1,732050808…
π = 3,14159265…
e = 2,718281828…
Classificação da dízima periódica: simples ou composta
As dízimas periódicas podem ser classificadas como simples ou compostas. Vamos ver agora como se dá essa diferenciação. Vem comigo!
Dízima periódica simples
Uma dízima periódica é simples, quando logo após a vírgula encontra-se o seu período, que segue infinitamente, sem que haja qualquer algarismo intruso.
Seguem alguns exemplos:
0,33333 …
2,66666 …
0,285714285714 …
Dízima periódica composta
Uma dízima periódica é composta, quando existe um grupo de um ou mais algarismos após a vírgula que não faz parte do seu período, ou seja, quando há a presença de algarismos intrusos, ou de antiperíodo. São exemplos:
1,3592929292 …
1,21616161616 …
0,00777777 …
Quem observou com atenção todos os exemplos, se deparou com a representação mais comum dos decimais periódicos.
Mas o fato é que existem pelo menos outras duas formas de representar uma dízima periódica. No próximo item, nós vamos entendê-las direitinho. Vem comigo!
Para fixar essas diferenças, veja o resumo comparativo a seguir:
| Característica | Dízima periódica simples | Dízima periódica composta |
| O que é | O período aparece logo após a vírgula, sem nenhum algarismo entre eles. | Existe um antiperíodo (algarismo ou grupo de algarismos que não se repete) entre a vírgula e o período. |
| Exemplo | 0,333… (período 3) | 1,3592929292… (antiperíodo 35, período 92) |
| Numerador da fração geratriz | O número correspondente ao período. | O número formado pela junção do antiperíodo com o período, menos o antiperíodo. |
| Denominador da fração geratriz | Um algarismo 9 para cada algarismo do período. | Um 9 para cada algarismo do período, seguido de um 0 para cada algarismo do antiperíodo. |
Como representar uma dízima periódica
A forma mais comum de representar uma dízima periódica é com as chamadas reticências, três pontinhos que indicam que os algarismos da dízima se repetem infinitamente.
Contudo, também é possível representar a mesma dízima sem repetir o período e acrescentar as reticências.
Para isto, basta escrever o decimal periódico apenas até o término de seu período, e em seguida, adicionar uma barra acima do número que representa o período.
Observem como isso se aplica aos exemplos que temos utilizado:
Com a escrita tudo certo, não é? No entanto, também precisamos entender como é possível ler esses números com clareza.
Mas isso é simples, não se preocupem. Faremos a leitura normalmente, e por fim, adicionaremos a palavra periódico, como no exemplo:
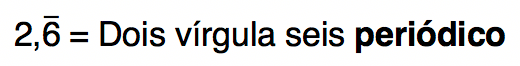
Entendido, pessoal? Bom, falamos uma série de vezes neste texto que a dízima periódica é um número racional, e, por isso, também pode ser representada sob a forma de fração.
Entretanto, encontrar a fração que representa um decimal periódico não é tão simples quanto escrevê-lo com a barra acima do período.
Vamos estudar esse processo através de dois macetes: um para a dízima periódica simples e outro para a dízima periódica composta. Sigam comigo!
Como encontrar a fração geratriz da dízima periódica
A fração que gera, ou que dá origem a uma dízima periódica, é chamada de fração geratriz. Toda fração é uma razão entre dois números inteiros, o numerador e o denominador.
Vocês vão ver na sequência, que dependendo da classificação da dízima periódica a ser analisada, vamos inserir alguns algarismos definidos no numerador e no denominador da sua respectiva fração geratriz. Vamos lá!
Fração geratriz da dízima periódica simples
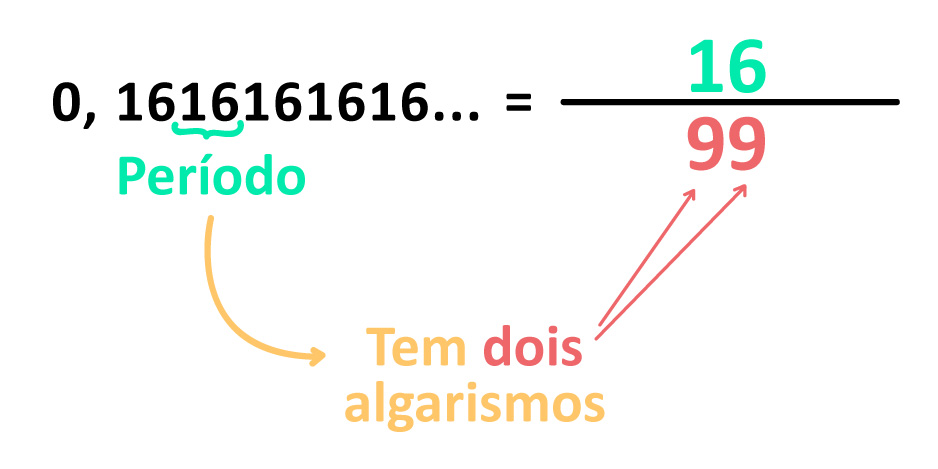
Para encontrar a fração geratriz de uma dízima periódica simples, basta inserir no:
- NUMERADOR: o número correspondente ao período da dízima periódica;
- DENOMINADOR: quantidade de “noves” correspondente ao número de algarismos que formam o período.
Fração geratriz da dízima periódica composta
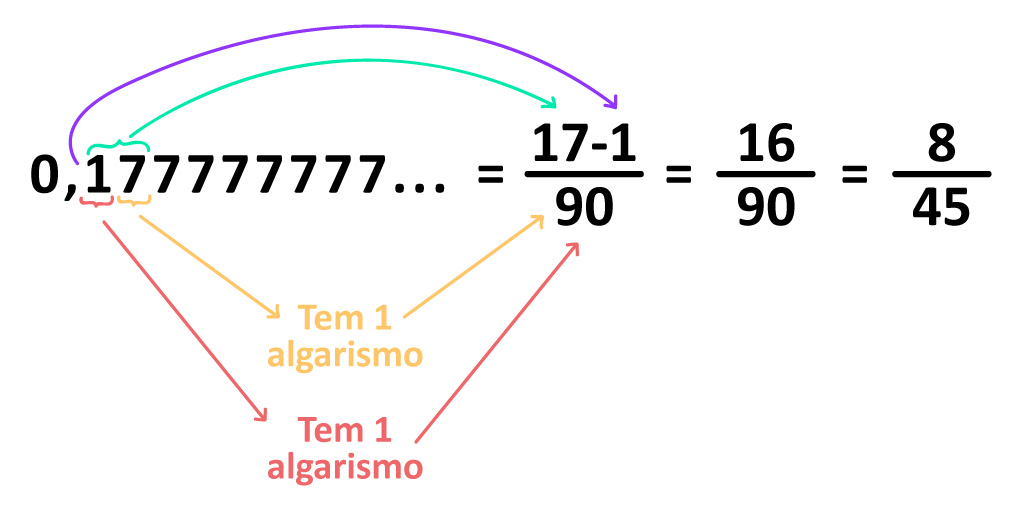
Para encontrar a fração geratriz de uma dízima periódica composta, basta inserir no:
- NUMERADOR: o resultado da subtração entre o número formado pela junção do antiperíodo com o período e o número formado somente pelo antiperíodo (intruso).
- DENOMINADOR: quantidade de “noves” correspondente ao número de algarismos que formam o período seguida pela quantidade de “zeros” correspondente ao número de algarismos que formam o antiperíodo (intrusos).
E aí, pessoal, o que acharam destes macetes? Vamos resolver agora uma série de exemplos para que tudo fique mais claro. Sigam comigo!
Exemplos resolvidos de fração geratriz da dízima periódica
Qual é a fração geratriz da dízima periódica 0,22222…?
Reparem, pessoal, que essa é uma dízima periódica simples. Por isso, podemos utilizar o macete da dízima periódica simples aqui. Lembram dele?
0,22222…
Período: 2
Quantidade de algarismos que formam o período: 1 → 1 “nove” no denominador
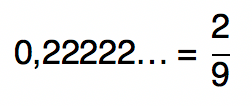
A fração geratriz da dízima periódica 0,22222… é 2/9.
Qual é a fração geratriz da dízima periódica 0,484848…?
Essa também é uma dízima periódica simples. Por isso, seguimos utilizando o mesmo macete.
0,484848…
Período: 48
Quantidade de algarismos que formam o período: 2 → 2 “noves” no denominador
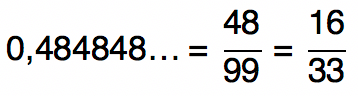
A fração geratriz da dízima periódica 0,484848… é 16/33.
Neste caso, a fração geratriz obtida através do macete não era irredutível, por isso, foi possível simplificá-la por 3.
Sempre que isso acontecer, pessoal, não hesitem em simplificar a fração geratriz encontrada!
Qual é a fração geratriz da dízima periódica 0,178787878…?
A dízima periódica 0,178787878… possui um algarismo intruso, o número 1.
Assim, para encontrarmos a sua fração geratriz, precisaremos utilizar o macete da dízima periódica composta. Olhem só!
0,178787878…
Antiperíodo: 1
Período: 78
Número formado pela junção do antiperíodo ao período: 178
Quantidade de algarismos que formam o período: 2 → 2 “noves” no denominador
Quantidade de algarismos que formam o antiperíodo: 1 → 1 “zero” no denominador
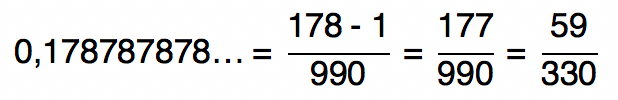
A fração geratriz da dízima periódica 0,178787878… é 59/330.
Qual é a fração geratriz da dízima periódica 0,66666666…?
0,66666666…
Período: 6
Quantidade de algarismos que formam o período: 1 → 1 “nove” no denominador
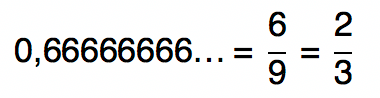
A fração geratriz da dízima periódica 0,66666666… é 2/3.
Qual é a fração geratriz da dízima periódica 0,4828282…?
0,4828282 …
Antiperíodo: 4
Período: 82
Número formado pela junção do antiperíodo ao período: 482
Quantidade de algarismos que formam o período: 2 → 2 “noves” no denominador
Quantidade de algarismos que formam o antiperíodo: 1 → 1 “zero” no denominador
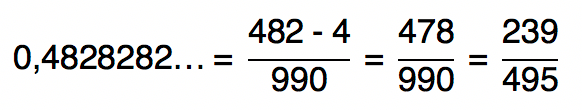
A fração geratriz da dízima periódica 0,4828282 … é 239/495.
Entendido, pessoal? Vejam que até agora nós não determinamos nenhuma fração geratriz de uma dízima periódica com parte inteira.
Quando isso for necessário, basta separar a parte inteira da parte decimal e utilizar os macetes que já aprendemos para encontrar a fração geratriz apenas da parte decimal.
Em seguida, é só somar a parte inteira a fração geratriz obtida. Acompanhem comigo este último exemplo!
Qual é a fração geratriz da dízima periódica 2,44444…?
A parte inteira da dízima periódica 2,44444… é o número 2, por isso, podemos reescrever esta dízima da seguinte forma:
2,4444… = 2 + 0,4444…
O número 0,44444… é uma dízima periódica simples. Assim, precisamos encontrar a sua fração geratriz.
0,44444…
Período: 4
Quantidade de algarismos que formam o período: 1 → 1 “nove” no denominador
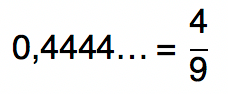
Por fim, resta-nos somar a fração 4/9 a parte inteira dada pelo número 2:
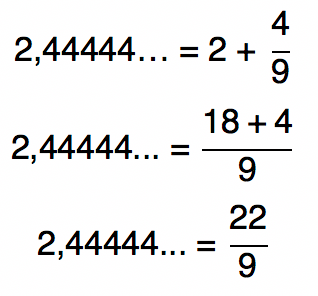
A fração geratriz da dízima periódica 2,44444… é 22/9.
Exercícios propostos
Agora que vocês já sabem encontrar a fração geratriz de qualquer dízima periódica, chegou a hora de praticar! Resolvam os exercícios a seguir e depois confiram as respostas no gabarito.
1) Determine a fração geratriz da dízima periódica 0,555…
2) Determine a fração geratriz da dízima periódica 0,363636…
3) Determine a fração geratriz da dízima periódica 0,2555…
4) Determine a fração geratriz da dízima periódica 0,124444…
5) Determine a fração geratriz da dízima periódica 3,1888…
6) Classifique as dízimas a seguir em simples ou composta, indicando o período e, quando houver, o antiperíodo: a) 0,777… b) 2,3181818… c) 0,04141414…
Gabarito
1) 5/9
2) 4/11
3) 23/90
4) 28/225
5) 287/90
6) a) Simples, período 7. b) Composta, antiperíodo 3, período 18. c) Composta, antiperíodo 0, período 41.
Incrível, não é mesmo? Assim, depois de tantos exemplos, é fato que precisamos encerrar este texto!
Espero que o conteúdo aqui abordado seja muito proveitoso para os seus estudos e que vocês possam aplicá-lo sempre que necessário.
Gostou do texto?! Continue seus estudos com os Cursos Gratuitos do Professor Ferretto.
Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da Plataforma do Professor Ferretto e vem com a gente garantir a sua vaga no ensino superior!
Perguntas frequentes sobre dízima periódica
Toda dízima periódica é um número racional?
Sim. Toda dízima periódica pode ser escrita na forma de fração — a sua fração geratriz — e todo número que pode ser representado como fração de dois inteiros pertence, por definição, ao conjunto dos números racionais (ℚ). Por isso, uma dízima periódica nunca é um número irracional.
Qual é a diferença entre dízima periódica simples e composta?
Na dízima periódica simples, o período aparece logo após a vírgula. Já na composta, existe um antiperíodo — um algarismo ou grupo de algarismos que não se repete — entre a vírgula e o período. A tabela apresentada neste texto resume essa diferença com exemplos.
Como saber se uma fração vai gerar uma dízima periódica?
Basta observar o denominador da fração já simplificada pelo MDC entre numerador e denominador. Se, além dos fatores 2 e 5, esse denominador tiver qualquer outro fator primo, a divisão resultará em uma dízima periódica. Se ele só tiver os fatores 2 e/ou 5, o resultado será um decimal exato.
0,999… (nove periódico) é igual a 1?
Sim. Usando o mesmo macete visto neste texto: se x = 0,999…, então 10x = 9,999…, e a subtração 10x − x resulta em 9x = 9, ou seja, x = 1. Por mais estranho que pareça à primeira vista, 0,999… e 1 são exatamente o mesmo número.
Nós estudamos aqui como obter a fração geratriz das dízimas periódicas através de macetes.
Mas, se vocês estão curiosos para saber qual é a essência deste processo, ou seja, porque determinamos aqueles padrões para o numerador e o denominador, vejam o vídeo que se encontra logo abaixo.
Nele, vocês também acompanham uma breve revisão que aborda todos os números decimais, e ainda, resolvem comigo alguns exercícios de vestibular!
Um abraço a todos e ótimos estudos!
Índice
Categorias
Últimos posts
Ver todas
