NÚMEROS PRIMOS E COMPOSTOS
17/10/2018
Olá pessoal, tudo bem com vocês?
Estamos aqui novamente, para abordar mais um assunto muito importante para a matemática básica: os números primos e compostos! A verdade, é que qualquer número natural diferente de zero e um pode ser definido como número primo ou como número composto, e cabe a nós descobrir como isso se dá através de um método bem interessante, que utiliza os famosos critérios de divisibilidade que já estudamos por aqui. Vocês não querem se deparar lá nas provas do ENEM e dos vestibulares com uma questão que envolve números primos ou compostos sem ter o devido conhecimento sobre eles, não é mesmo? Então não dá para perder o texto de hoje!
Mas se além da matemática básica, alguns tópicos de toda a matemática do ensino médio também forem um problema pra vocês, então não dá para perder a oportunidade de assinar a plataforma do Professor Ferretto! O curso de matemática do Professor Ferretto é um curso online que tem foco na melhor preparação para o ENEM e os tradicionais vestibulares do país. Tudo surgiu com o YouTube, porém a necessidade de disponibilizar um curso completo, fez com que surgisse essa plataforma moderna de estudo, na qual, vocês alunos, garantem um aprendizado absoluto para conquistar a tão sonhada vaga num curso de nível superior! Não percam mais tempo, pessoal! Acessem o site para conhecer todos os benefícios oferecidos na plataforma!
Bom, como foi dito logo acima, qualquer número natural diferente de zero e um pode ser definido como número primo ou como número composto. Mas vocês lembram quais números pertencem ao conjunto dos números naturais? Pois então, são esses aí abaixo:
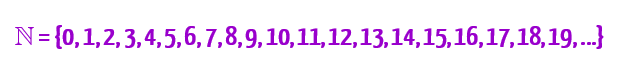
Agora que já conhecemos todos os números naturais, nada mais justo do que entendermos quais deles são primos, e quais deles são compostos. Vocês vão ver através das definições abaixo, que nenhum número natural pode ser primo e composto ao mesmo tempo.

Observem a sequência de números acima: todos eles são números primos, porque só podem ser divididos por 1 e por eles mesmos sem deixar restos. Agora, o fato mais interessante, é que de todos esses números, e também daqueles que seguem infinitamente e são representados pelas reticências (…), somente um deles é um número par: o número 2!

O número dois é o único número primo que é par. Os demais números primos são todos ímpares.
Aí, se vocês compararem a sequência de números acima com o conjunto dos números naturais por completo, verão que além dos demais números pares do conjunto, também estão faltando mais alguns números ímpares na sequência. Pois é pessoal, ser um número ímpar não significa necessariamente ser um número primo também. A definição de número composto vai tornar isso mais claro para vocês.

A sequência acima nos mostra uma série de números compostos. Qualquer um desses números pode ser dividido por 1, por ele mesmo, mas também por outros 1, 2, 3, 4, 5 ou mais divisores, e é justamente esse detalhe que não faz deles números primos. Como vocês podem ver nessa sequência, os números ímpares que ali se encontram são divisíveis por outros números além de 1 e deles mesmos, e um exemplo disto é o número 21, que é divisível por 3 e 7, além de ser divisível por 1 e pelo próprio 21.
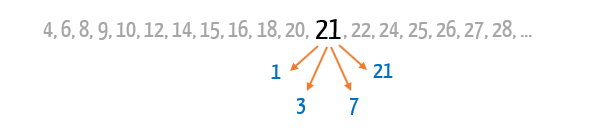
É claro que isso também acontece com todos números pares que ali se encontram. Um exemplo é o número 12, que pode ser dividido por 2, 3, 4, e 6, além ser divisível por 1 e por ele mesmo. Qualquer número par que não seja o 2, sempre será considerado um número composto.

Agora que vocês já sabem o que é um número primo e o que é o número composto, fica bem mais fácil de entender porque os números zero e um não se encaixam em nenhuma dessas duas definições. Deem uma olhada nas operações abaixo:
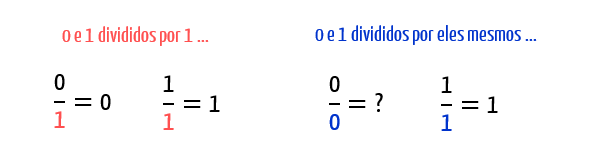
O primeiro ponto a ser observado, é que tanto zero quanto um não possuem mais do que 2 divisores distintos. Isso já os exclui da definição de número composto. Agora, o segundo ponto a ser observado, é que apesar de não haver problema quanto a divisão de zero e um por 1, já que o número 1 é considerado o divisor universal, e portanto, pode dividir qualquer número real, a divisão de zero e um por eles mesmos gera 2 conflitos que os impedem de se adequarem a definição de números primos, olhem só:
- A divisão de zero por zero é considerada uma indeterminação matemática, e portanto, não é válida para o caso;
- A divisão de um por um, representa a mesma operação que a divisão de um por ele mesmo.
Isso mostra que tanto zero quanto 1 não tem dois divisores naturais distintos ou diferentes, mas somente um, que é o próprio 1.
Entendido, pessoal? Depois de estudarmos todas essas definições, finalmente é chegada a hora em que vamos descobrir como determinar, na prática, se um número natural é primo ou composto. Como qualquer número natural maior ou igual a dois não pode ser ao mesmo tempo um número primo e composto, a ideia consiste basicamente em definir se o número desejado é primo. Se ele não for primo, será composto, e pronto!
Pois é, mas vocês sabem como determinar se um número natural é primo? Não? Então aí vai a regra que pode estabelecer tudo isso:

Realizar divisões sucessivas por números primos, significa basicamente dividir o número desejado por 2, 3, 5, 7, 11, 13 e pelos demais números primos seguintes, até que se obtenha uma divisão na qual o resto é diferente de zero, e o divisor (d) é maior ou igual ao quociente (q). Quando isso acontecer, haverá a certeza de que tal número é mesmo primo. No entanto, se porventura, pelo caminho, alguma dessas divisões por números primos gerar um resto igual a zero, significa que tal número possui pelo menos outro divisor além de 1 e dele mesmo, o que fará dele um número composto.
Entenderam a ideia? Tenho certeza de que com um exemplo tudo ficará mais fácil. Vamos começar resolvendo um exercício da maneira mais simples e didática possível, para na sequência, utilizar alguns conceitos que podem facilitar e agilizar ainda mais o processo. Vem comigo aqui!
143 é um número primo?
Começaremos dividindo 143 por 2.
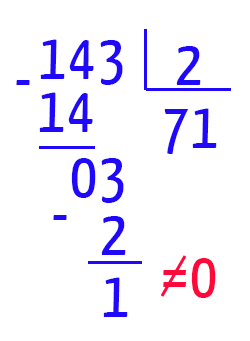
Vejam que nessa divisão, obtivemos um resto diferente de zero, e um quociente maior do que o divisor da operação (71 > 2). Isso significa que 143 ainda é um candidato a ser número primo, mas como não temos certeza, iremos a próxima divisão!
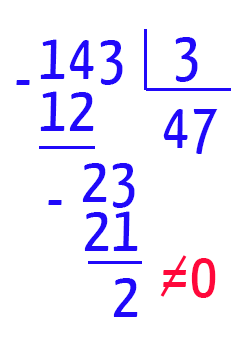
Novamente, temos um resto diferente de zero e um quociente maior que o divisor (47 > 3). Ainda há possibilidade de 143 ser um número primo, mas para confirmar, devemos continuar até que o divisor seja maior ou igual ao quociente.
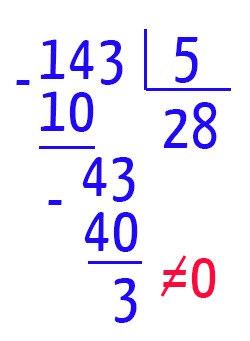
Olhem só! Nesta nova divisão, ainda temos um resto diferente de zero, no entanto, o quociente permanece maior que o divisor (28 > 5). Só nos resta continuar…
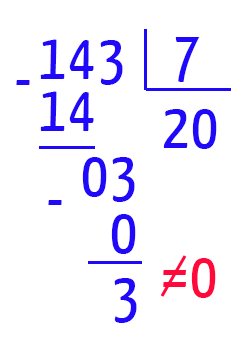
Mas que coisa! Ainda temos um resto diferente de zero e um quociente maior que o divisor (20 > 7). Vamos a uma nova divisão pelo número primo da sequência, o 11.
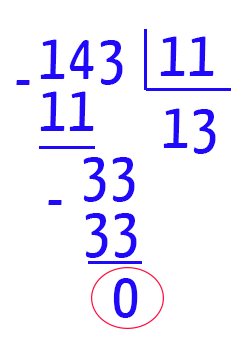

Pois é, parece que acabamos de descobrir que 143 é um número composto, afinal, ele é divisível por 1, por ele mesmo, e pelo menos por 11 também.

Pessoal, infelizmente não há como fugir desses cálculos quando o intuito é estabelecer se um número é primo ou não. De prático, esse método realmente não tem nada, mas para a alegria de vocês existe sim um jeito de dar uma acelerada no processo, quando se conhece os critérios de divisibilidade.
Os critérios de divisibilidade são pequenas regras que utilizamos para determinar se um número inteiro qualquer é divisível por 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 e daí por diante. Se nós utilizarmos essas regras, poderemos definir sem realizar cálculo algum quando o resto de uma divisão por 2, 3, 5, 7, 11, será diferente de zero ou não. Querem ver como funciona? Então vamos a mais um exemplo!
223 é primo?
Bom, o primeiro passo para estabelecermos se 223 é um número primo, seria dividir esse número por 2. Mas, segundo os critérios de divisibilidade, apenas os números pares são divisíveis por 2. Assim, sendo 223 um número ímpar, é fato que a divisão de 223 por 2 gerará um resto diferente de zero. Isso significa que 223 ainda é um candidato a ser primo, e que podemos pular para o próximo passo!
Então, seria chegada a hora de dividir 223 por 3. Contudo, é verdade que um número é divisível por 3, quando a soma de seus algarismos resulta em um número divisível por 3. Vamos ver se isso acontece por aqui!
2 + 2 + 3 = 7
Sete não é, nem de longe, um número divisível por 3. Por isso, a divisão de 223 por 3 certamente gerará um resto diferente de zero, o que faz com que ele ainda seja um candidato a ser primo!
Aí, faríamos a divisão de 223 por 5. Mas é fato que um número é divisível por 5, quando seu último algarismo é zero ou 5. Como 223 termina com o número 3, ele jamais poderá ser dividido por 5 sem gerar um resto diferente de zero. Desta forma, 223 ainda é um possível número primo.
Agora, seguiríamos para a divisão por 7. Mas nesse caso é o que realmente vamos fazer. Quem leu o texto Critérios de Divisibilidade, sabe que utilizar o critério de divisibilidade por 7, é quase mais demorado do que realizar a própria divisão em si.
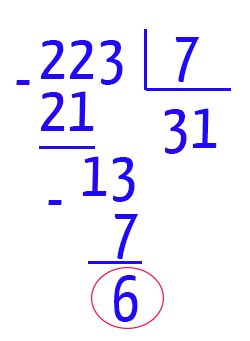
Vejam que essa divisão gerou um resto diferente de zero e um quociente maior que o divisor (31 > 7). 223 ainda pode ser um número primo, e o jeito é continuar calculando!
E lá viria a divisão de 223 por 11. Mas felizmente, um número é divisível por 11, se a soma alternada de seus algarismos resultar em um número divisível por 11. Então vamos ver se isso funciona por aqui!
+2 – 2 + 3 = 3
Três não é um número divisível por 11. Isso nos mostra que a divisão de 223 por 11 certamente geraria um resto diferente de zero. Como o próximo número primo positivo da sequência é o 13, vamos realizar uma nova divisão. Não parece, mas estamos perto do fim, acreditem!
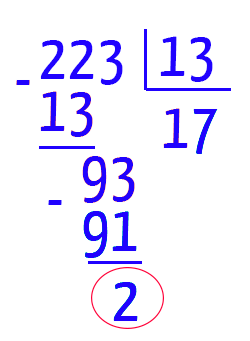
Observem que a divisão de 223 por 13 também gerou um resto diferente de zero, mas o quociente permanece maior do que o divisor (17 > 13). Felizmente, essa realidade irá mudar no próximo passo, pois o divisor está se aproximando cada vez mais do quociente. Fiquem atentos ao que irá acontecer!

Eba! A divisão de 223 por 17 gerou um resto diferente de zero e um divisor maior que o quociente! Já não era sem tempo! Acabamos de determinar, com toda a certeza, que 223 é um número primo!
Fácil, não é pessoal? Só é um pouquinho demorado. Mas tenho certeza que a medida em que vocês forem resolvendo uma série de exemplos, e memorizando direitinho os principais critérios de divisibilidade, tudo ficará mais rápido e claro! Já vou avisando que o vídeo que está em anexo está imperdível hoje! Nele vocês encontram uma abordagem complementar a tudo que estudamos por aqui, e ainda, a resolução de um exercício que envolve números primos juntamente a alguns conceitos fascinantes da aritmética! Espero que vocês tenham gostado do texto, e que continuem acompanhando todos os conteúdos disponibilizados aqui no blog!
Um abração! Bons estudos a todos!