GRÁFICO DA FUNÇÃO DO 1º GRAU
11/10/2018
Olá pessoal! Tudo tranquilo?
O gráfico de uma função do primeiro grau, cujo formato é f(x) = ax + b, será sempre uma reta! Aqui no blog, nós já abordamos uma série de aspectos que envolvem essa função, também conhecida como função afim, mas nunca havíamos falado sobre a construção da reta em si. Bom, isso foi até hoje! Neste texto, nós vamos construir alguns gráficos de funções do 1º grau de maneiras muito simples, tudo para que vocês possam usar esse conhecimento para construir o gráfico de qualquer função matemática!
E olhem só que interessante: a função do primeiro grau é bastante utilizada em diversos assuntos práticos, todos ligados a questões que envolvem linearidade, e, portanto, podem ser representados por uma reta. Por isso, a representação gráfica dessas questões pode nos ajudar, e muito, a interpretar determinadas situações, inclusive, nos poupando uma série de cálculos. Interpretar, poupar cálculos, essas palavras não lembram nada a vocês? Pois é, elas representam elementos cruciais quando se pensa em prestar as provas do ENEM e dos vestibulares! Mas quem deseja mandar bem nessas provas, certamente já assinou, ou vai assinar a plataforma do Professor Ferretto, não é mesmo? Só lá tem videoaulas sobre toda a matemática do ensino médio, planos de estudo personalizados, centenas de exercícios do ENEM e de vestibulares com resolução em vídeo, e até monitoria no plano diamante. E se vocês acham que são só essas as vantagens, eu aviso: não, tem muito mais! Acessem o site para conferir todas elas!
Ansiosos para começar? Então, vamos lá! Nós afirmamos bem no início do texto, que o gráfico de uma função do 1º grau é sempre uma reta. Mas vocês sabem o que significa exatamente o termo “reta”?
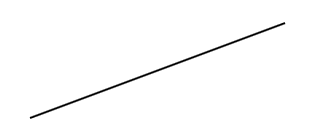
No dicionário, de forma geral, diz-se que uma reta é um “traço que segue uma única direção, sem curvas ou ângulos”. Bom, a imagem acima nos mostra que de fato é isso mesmo. Mas a verdade é que o comprimento, ou a medida da reta que vemos acima, é apenas uma questão de representação: uma reta é formada por infinitos pontos, e por isso o seu comprimento é dito como infinito.

Agora, será mesmo que para construirmos uma reta seria necessário definir todos os seus infinitos pontos? Não, né pessoal! Primeiro, porque algo infinito teoricamente não tem fim, e aí passaríamos a vida toda construindo uma reta. E segundo, mas não menos importante, porque a definição geométrica da reta nos diz que “uma reta é o menor caminho entre dois pontos”.
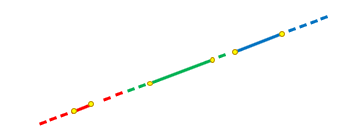
E não é que é verdade mesmo? Vejam na figura acima, que se obtermos quaisquer dois pontos de uma reta, ligarmos esses pontos, e depois continuarmos traçando a reta para ambos os lados seguindo a mesma direção, então teremos o comportamento preciso da reta como um todo! Tendo isso em vista, é claro que fica muito mais fácil construir o gráfico da função afim!
Bom, para que essa ideia fique bem clara, nada melhor do que a colocar em prática! É isso que faremos na sequência, de duas maneiras diferentes. Então pegue um lápis, papel, e vem comigo aqui!
Construa o gráfico das seguintes funções:
a) f(x) = 2x – 1
Nós acabamos de descobrir que precisamos de apenas dois pontos, ou duas coordenadas do plano cartesiano, para construir uma reta, não é mesmo? Pois bem, para obtermos esses dois pontos, nós utilizaremos nesse primeiro exemplo a famosa tabelinha, e nela, vamos substituir a variável x da função f(x) = 2x – 1 por dois valores de nossa escolha, a fim de encontrarmos os seus respectivos valores em y, porque como vocês sabem, uma função f(x) = ax + b também pode ser escrita na forma y = ax + b.
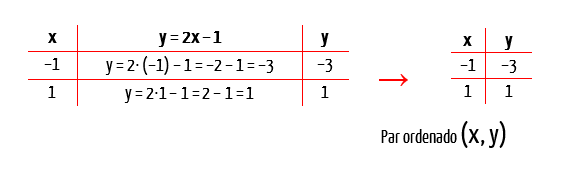
Vejam que nós atribuímos a variável x os valores –1 e 1, e descobrimos que seus valores em y são respectivamente –3 e 1. Agora temos duas coordenadas cartesianas, formadas pelos pares ordenados (–1, –3) e (1, 1), e a partir delas, poderemos encontrar dois pontos no plano cartesiano. Mas é claro que vocês poderiam ter escolhido quaisquer outros valores, e obtido quaisquer outros pares ordenados. Tenho certeza de que a reta que vamos construir abaixo seria exatamente a mesma, independente dos pontos utilizados para encontrá-la.
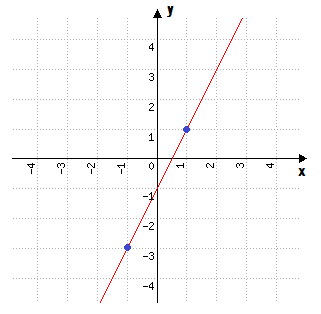
Viram como é fácil? Basta ligarmos os dois pontos que encontramos, e seguir traçando a reta na mesma direção além deles. Pessoal, o método da tabelinha pode ser utilizado para construir o gráfico de qualquer função matemática, portanto, vocês podem utilizá-lo sempre e, inclusive, devem aproveitar para fazer isso quando se trata da função do 1º grau, afinal, apenas dois pontos conseguem definir o comportamento de uma reta, o que nem sempre acontece nas demais funções.
Agora, é fato que vocês possam estar se perguntando: vou precisar escolher sempre os valores que atribuo a x? Dependendo da função isso não é arriscado? Não existe um método diferente em que eu não dependa das minhas escolhas? Se isso realmente aconteceu com vocês, eu tenho uma boa notícia: no próximo exemplo, será utilizado um método que nos permite eliminar as escolhas dos pontos utilizados para traçar a reta. Nesse novo método, nós trabalharemos com os pontos em que a reta corta ou intersecta os eixos cartesianos. Acompanhem com atenção!
b) y = – x + 2
Nós estudamos no texto Noções básicas de plano cartesiano, que quando os pontos se localizam exatamente sobre o eixo x ou sobre o eixo y, as suas coordenadas possuem uma configuração específica. Qualquer ponto que se localize exatamente sobre o eixo das abscissas, ou sobre o eixo x, por exemplo, sempre terá a configuração (x, 0), de forma que o valor de y certamente será zero. Agora, quando um ponto qualquer se localiza exatamente sobre o eixo das ordenadas, ou sobre o eixo y, acontece justamente o contrário: esse ponto terá a configuração (0, y), o que significa que o valor de x certamente será zero. Por isso, quando desejarmos obter o ponto em que a reta corta o eixo x, nós substituiremos o valor de y na função por zero:
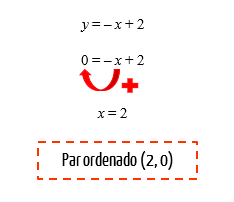
Se vocês repararem no cálculo que fizemos acima, poderão perceber que na verdade, quando buscamos o ponto onde o gráfico corta o eixo x, nós estamos obtendo a raiz da função. Incrível, não é? Mas se desejarmos obter o ponto em que a reta corta o eixo y, então deveremos substituir o valor de x na função por zero:

Conhecendo esses dois pontos, nós estamos prontos para construir a reta que representa a função y = – x + 2. Mas antes disso, aí vai uma dica muito interessante: nós aprendemos no texto Introdução a função afim, a distinguir os coeficientes a e b da função do primeiro grau. Mas o que não foi dito ainda, é que o coeficiente b, que é o famoso termo independente da função afim, representa justamente o ponto onde o gráfico corta o eixo y!

Depois dessa dica maravilhosa, nada melhor do que traçarmos a tão esperada reta representativa da função y = – x + 2.
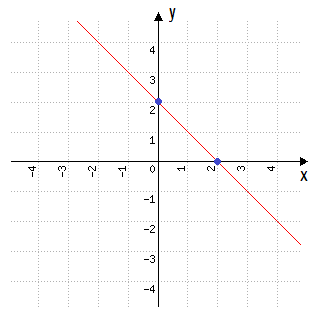
Ficou claro. pessoal? Resumindo essa última ideia, é fato que podemos construir o gráfico de uma função do primeiro grau somente conhecendo a raiz dessa função, que representa o ponto no qual o gráfico corta o eixo x, e observando o coeficiente b dessa mesma função, já que ele representa o ponto em que o gráfico corta o eixo y, e pronto! É claro que vocês podem continuar utilizando a tabelinha em conjunto com esse conceito, ou podem utilizar somente a tabelinha, isso fica a critério de vocês! Só não dá para deixar de encontrar pelo menos dois dos pontos que pertencem a reta que vocês desejam representar!
E para fecharmos o assunto com chave de ouro, vocês lembram que no início do texto nós falamos sobre a utilização prática do gráfico da função do primeiro grau? Pois então, no vídeo que está em anexo, vocês encontram um exemplo resolvido que envolve questões financeiras, e em um caso como esse, a representação gráfica das funções pode ajudar e muito a entendermos o contexto da situação. Gráfico é visualização, informação apresentada de forma simples e de fácil compreensão, que pode substituir um grande texto ou mesmo uma série de equações. Por isso, é imprescindível que vocês saibam interpretar os gráficos direitinho, eles aparecem com frequência nas provas do ENEM, vestibulares, e mesmo no cotidiano. Hoje o convite para assistir o vídeo ficou irrecusável, não é mesmo?
Bom, infelizmente o texto termina por aqui! Um abração, e uma ótima semana de estudos a todos!