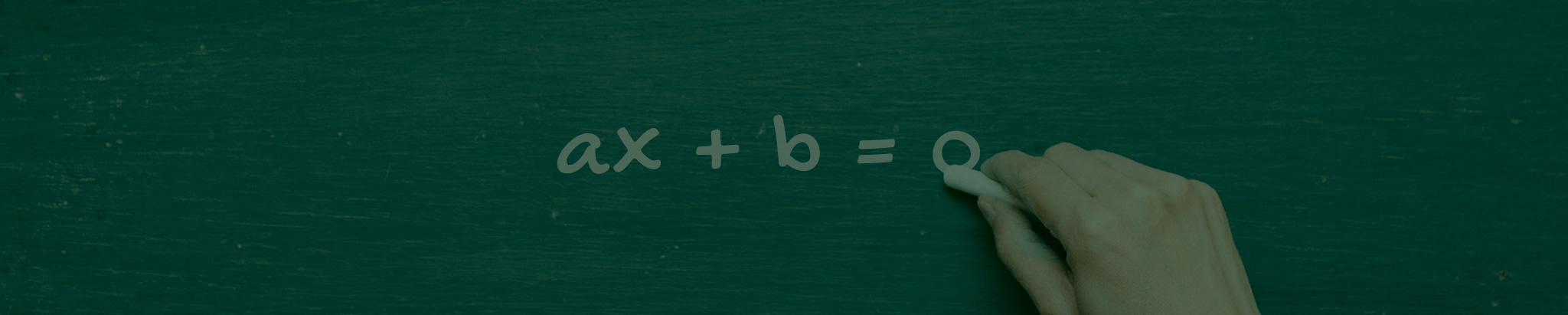COEFICIENTE ANGULAR DA FUNÇÃO AFIM
14/02/2020
O coeficiente angular de uma função do 1º grau está intimamente ligado a inclinação da reta – a forma gráfica da função afim – em relação ao eixo x. Além disso, também podemos entender o coeficiente angular como uma taxa de variação constante, que pode ser positiva ou negativa.
Olá, pessoal! Tudo bem com vocês?
Hoje nós vamos falar sobre o coeficiente angular da função afim, que também costuma ser chamada de função polinomial do 1º grau. A função do primeiro grau é uma das mais funções mais abordadas no ENEM e nos vestibulares tradicionais, visto que ela representa um comportamento linear, que se aplica a muitos fenômenos do nosso cotidiano. Mas não se preocupem! Depois de ler este texto, vocês entenderão direitinho o que é o coeficiente angular, onde ele se localiza na função afim e claro, como é possível calculá-lo.
Entendido, pessoal? Então, que tal iniciarmos os estudos? Fiquem à vontade para anotar todos os conceitos que vamos aprender daqui pra frente. Venham comigo!
1. O QUE É O COEFICIENTE ANGULAR DA FUNÇÃO AFIM?

A fórmula matemática da função afim possui dois coeficientes, ou seja, dois termos que costumam assumir valores numéricos. O coeficiente angular a é o coeficiente que está junto da variável x, e o coeficiente linear b é o chamado termo independente da função. Neste texto, nós iremos tratar apenas do coeficiente angular da função afim. Portanto, ficaremos de olho no que o valor de a nos traz de informação acerca desta função e da representação gráfica dela.
O gráfico da função afim f: ℝ → ℝ dada por ƒ(x) = ax +b, em que a ≠ 0, é uma reta. O coeficiente de x, a, é chamado coeficiente angular ou declividade da reta e está ligado a sua inclinação em relação ao eixo x, o eixo das abscissas.
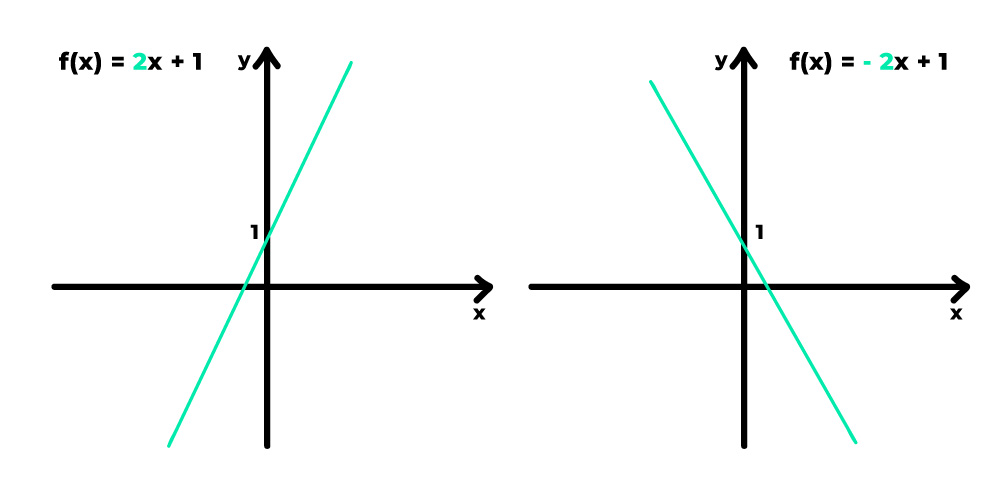
Observem os dois gráficos acima e fiquem atentos a diferença entre eles. Quando o coeficiente angular de uma função afim é um valor positivo ou maior que zero (a > 0), o gráfico da função é uma reta crescente. Do contrário, ou seja, quando o coeficiente angular é um valor negativo ou menor que zero (a < 0), o gráfico da função é uma reta decrescente.
1.1 O ângulo de inclinação da reta de acordo com o valor do coeficiente angular a
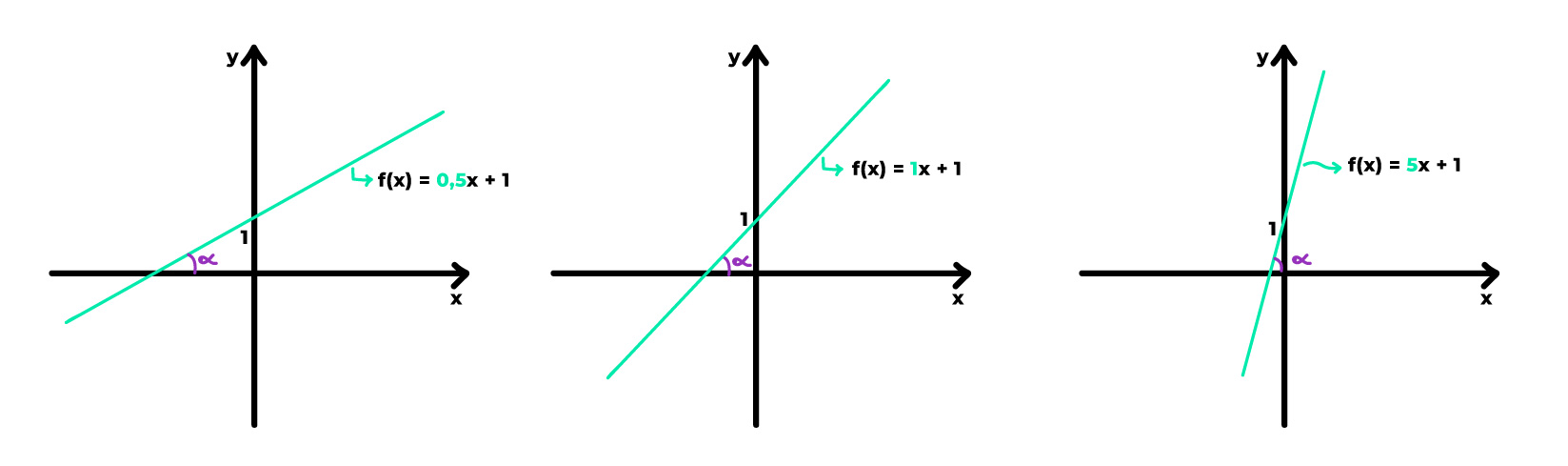
Na imagem acima, vemos 3 gráficos de funções do 1º grau diferentes. Reparem na mudança de comportamento das retas de acordo com o valor do coeficiente angular a, quando este é positivo. Quanto mais próximos de zero são os valores de a, mais próximo de 0º é o ângulo de inclinação da reta com relação ao eixo x. Na medida em que os valores do coeficiente a vão aumentando, o ângulo de inclinação da reta em relação ao eixo x vai se aproximando de 90º.
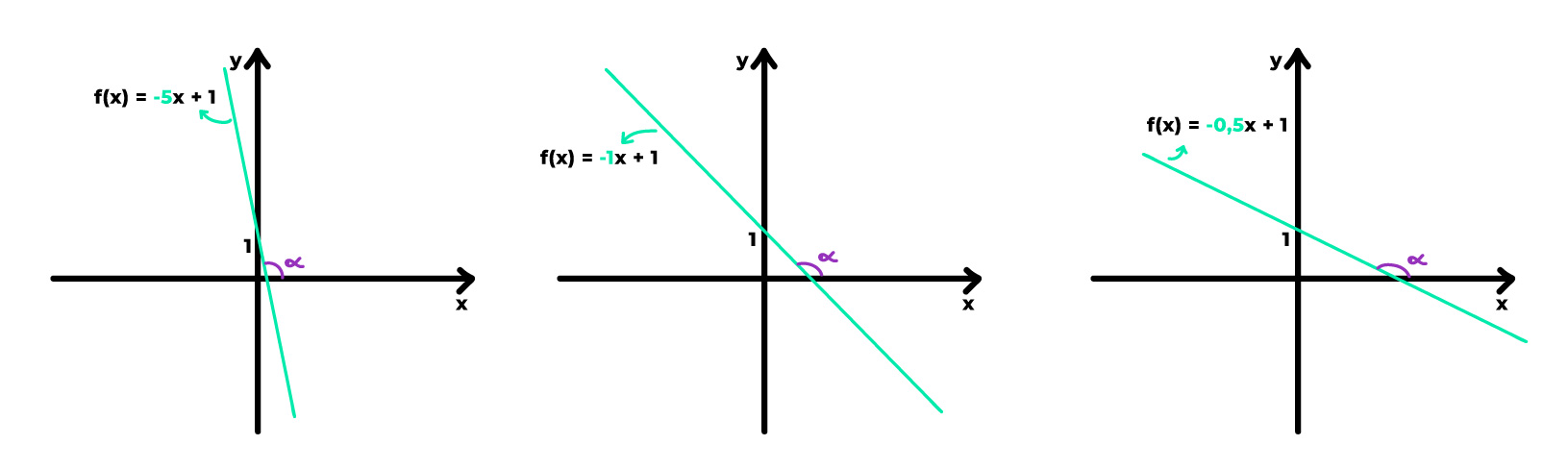
Já quando o valor de a é negativo, ou seja, quando o gráfico da função afim é uma reta decrescente, na medida em que os valores de a são muito negativos, o ângulo de inclinação da reta com o eixo x é muito próximo de 90º. Contudo, na medida em que os valores de a são cada vez menos negativos e se aproximam de zero, o ângulo de inclinação da reta com o eixo x se aproxima de 180º.
Incrível, não é, pessoal? Reparem que em nenhum momento foi apresentado o comportamento do gráfico da função afim para um coeficiente a de valor zero. Isso aconteceu porque, vocês sabem, a não pode ser um valor nulo. Quando a vale zero, tem-se o que chamamos de função constante. O gráfico da função constante é uma reta horizontal, paralela ao eixo x.
Bom, já sabemos como o valor do coeficiente angular influencia no comportamento do gráfico da função afim. Agora chegou o momento de aprendermos a calcular este coeficiente. É isso que faremos no próximo item, mas antes, fica o seguinte conselho: se vocês não entenderam como encontrar o coeficiente angular a na função afim, cliquem aqui! Este e vários outros aspectos importantes da função do 1º grau são abordados aqui no blog!
Entendido? Então, sigam comigo!
2. COMO CALCULAR O COEFICIENTE ANGULAR?
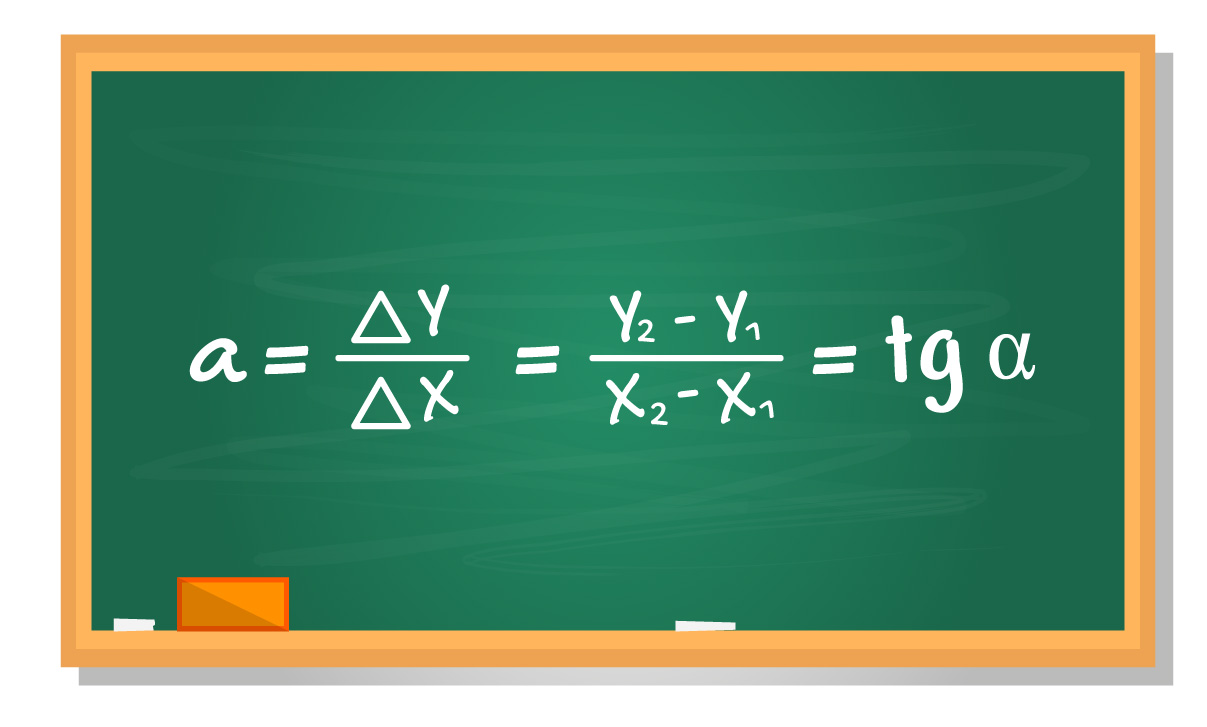
É possível calcular o coeficiente angular da função afim de 3 formas diferentes. Graficamente, aplicando o conceito de taxa de variação, conhecendo dois pontos de uma reta, ou então, o ângulo de inclinação da reta com o eixo x. Vamos estudar cada uma delas logo mais. Vem comigo!
2.1 O coeficiente angular como taxa de variação
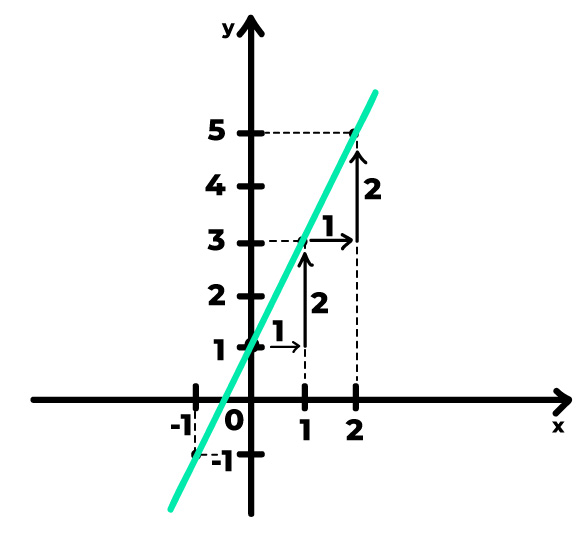
A taxa de variação de uma função afim nada mais é do que a razão entre a variação no eixo y e a variação correspondente no eixo x. Dessa forma, para calcular o coeficiente angular de uma função afim conhecendo apenas o gráfico desta função, basta seguir os seguintes passos, olhem só!
1º Passo: observe se a reta é crescente ou decrescente
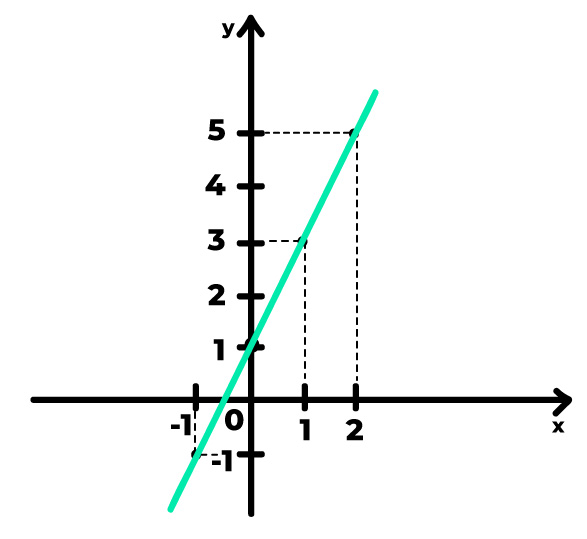
Indiscutivelmente, a reta que vemos acima é crescente. Dessa forma, sabemos que o seu coeficiente angular é um valor positivo (a > 0). Caso a reta deste exemplo fosse decrescente, saberíamos que o seu coeficiente angular seria negativo (a < 0), e assim, seria necessário acrescentar o sinal negativo ao final do cálculo.
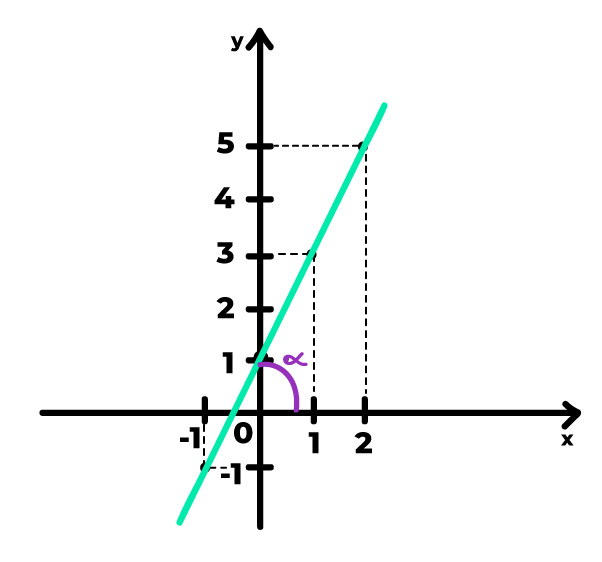
2º Passo: escolha quaisquer dois pontos do gráfico
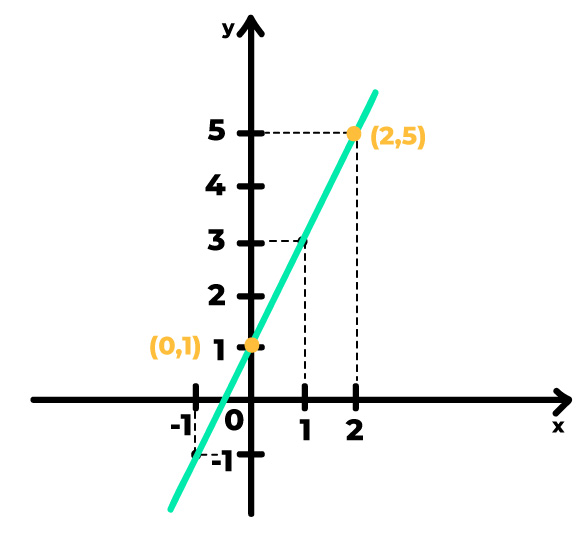
Neste exemplo, escolhemos os pontos (0,1) e (2,5), mas poderíamos ter optado por quaisquer outros dois pontos da reta. Na função do primeiro grau, a taxa de variação é sempre constante, de forma que o coeficiente angular pode ser calculado a partir de qualquer região do gráfico. Agora estamos prontos para seguir até o próximo passo. Vem comigo!
3º Passo: Identifique qual é a variação no eixo y e a qual é a variação no eixo x entre os dois pontos escolhidos e obtenha a razão entre esses dois valores
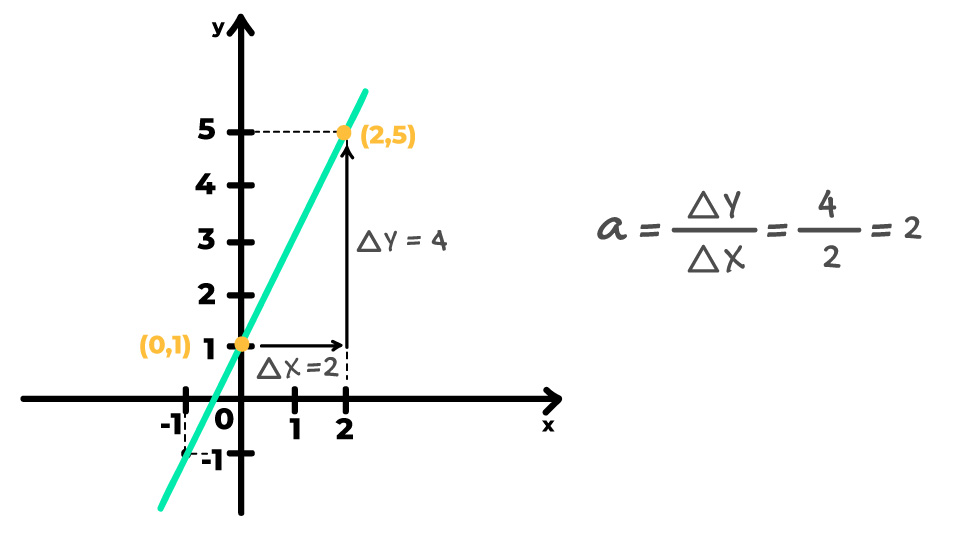
Analisando o gráfico, podemos perceber que a variação nos eixos x e y entre os pontos escolhidos é, respectivamente, 2 e 4. Isso porque no eixo x, saímos do ponto zero e chegamos ao ponto 2, ou seja, percorremos 2 unidades. No eixo y saímos do ponto 1 e fomos até o 5, percorrendo 4 unidades.
Quem não conseguiu perceber essas variações apenas observando o gráfico, pode utilizar diretamente o próximo método que nos permite encontrar o coeficiente angular a. Acompanhem!
2.2 O coeficiente angular quando dois pontos de uma reta são conhecidos
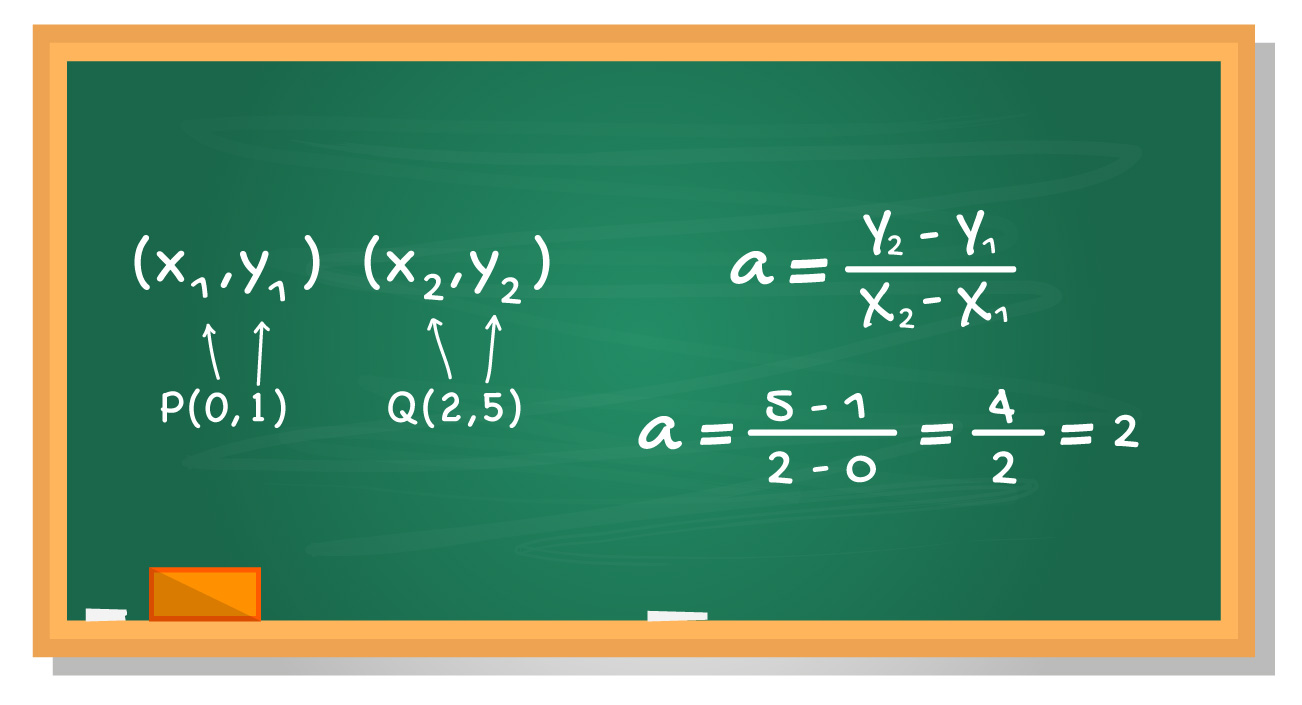
Quando pelo menos dois pontos de uma reta são conhecidos, fica ainda mais fácil determinar o seu coeficiente angular. Basta utilizar a fórmula apresentada no quadro acima! Um dos pontos conhecidos terá coordenadas (x1, y1) e o outro terá coordenadas (x2, y2).
Um detalhe importante nesse caso, é que o cálculo do coeficiente angular a pode ser feito de duas formas diferentes. No caso do exemplo, consideramos que o ponto P teria as coordenadas (x1, y1) e o ponto Q teria as coordenadas (x2, y2). Vamos refazer o cálculo considerando que o ponto Q terá coordenadas (x1, y1) e que o ponto P terá as coordenadas (x2, y2). Fiquem de olho no resultado desse cálculo:
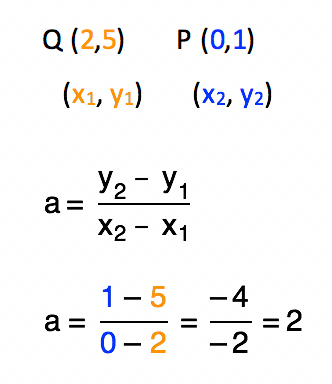
Legal, não é pessoal? Agora, vamos a última maneira de calcular o coeficiente angular a. Sigam comigo!
2.3 O coeficiente angular quando o ângulo de inclinação da reta é conhecido
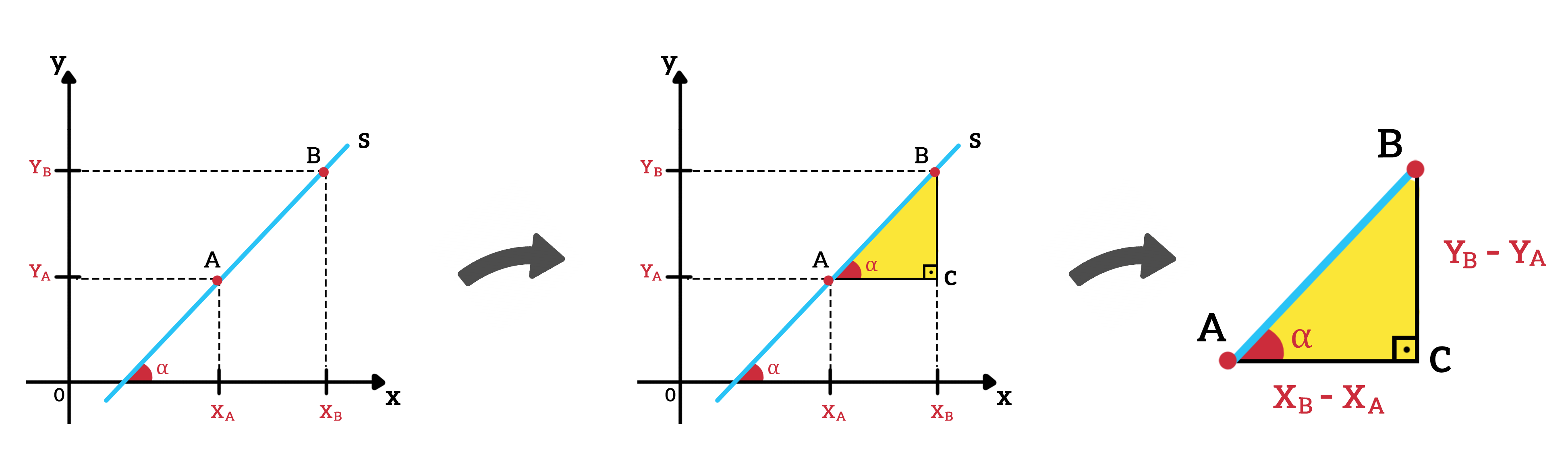
Até agora, apesar de sabermos que o coeficiente angular a está intimamente ligado ao ângulo que a reta, o gráfico da função afim, forma em relação ao eixo x, pensamos nele apenas como um valor real, não envolvemos os ângulos no assunto. Mas a verdade é que toda vez que escolhemos dois pontos em uma reta, podemos construir ali um triângulo retângulo. As medidas dos catetos deste triângulo retângulo são as variações em y e em x.
Ora, se as medidas dos catetos oposto e adjacente ao ângulo de inclinação da reta são conhecidas, é claro que podemos encontrar o ângulo 𝛼 através da razão trigonométrica tangente.
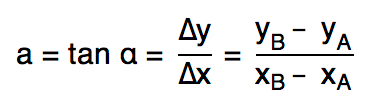
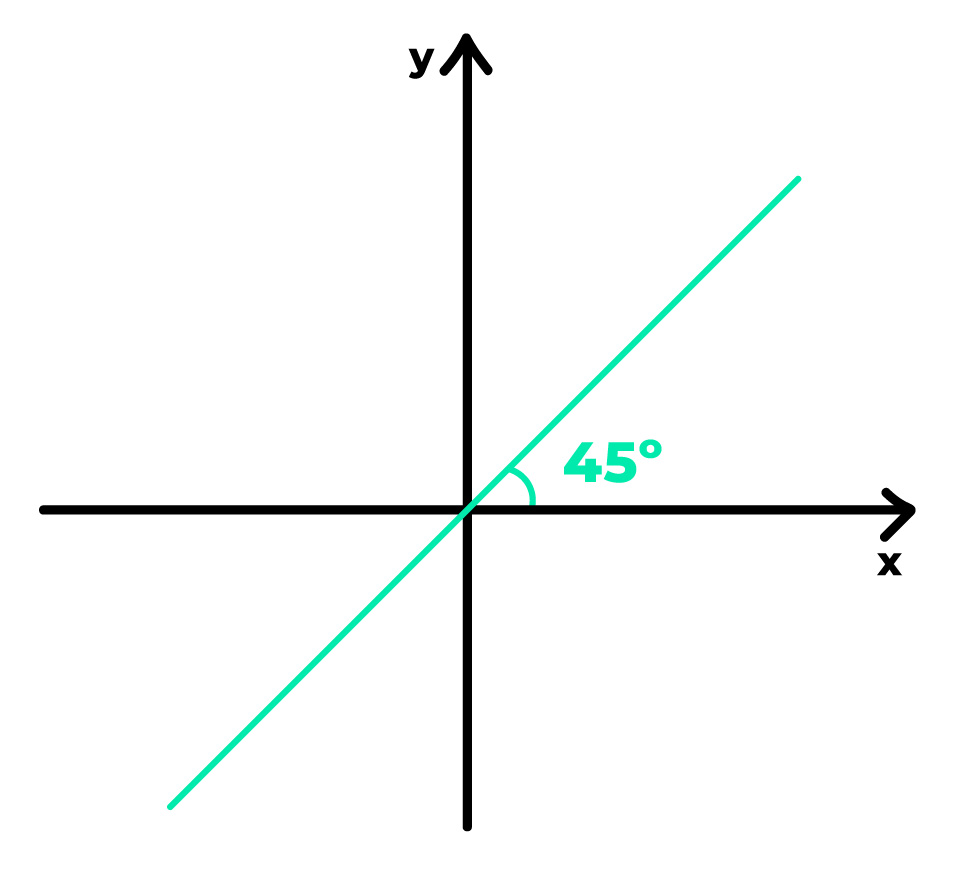
E aí, qual é o coeficiente angular da reta acima? Muito simples, basta descobrirmos quanto vale a tangente do ângulo de 45º.
a = tan (45º) = 1
Conforme essa ideia, vamos voltar nossa atenção a reta que utilizamos para calcular o coeficiente angular a diversas vezes neste texto. Qual será o valor do ângulo de inclinação 𝛼, sabendo que o coeficiente angular que encontramos é igual a 2? Neste caso, basta aplicarmos a tangente inversa ao coeficiente angular.
𝛼 = tan-1(a)
𝛼 = tan-1(2) = 63,43º
E aí, o que acharam deste texto, pessoal? Espero que ele tenha sido proveitoso para a preparação de vocês rumo as provas do ENEM e dos vestibulares! Para que o conteúdo aprendido hoje fique ainda mais claro, deixo aqui embaixo algumas questões para vocês resolverem. Não deixem de conferir a resolução em vídeo depois!
3. EXERCÍCIOS DO ENEM E DE VESTIBULARES RESOLVIDOS EM VÍDEO

1) (ENEM) Uma cisterna de 6 000 L foi esvaziada em um período de 3 h. Na primeira hora foi utilizada apenas uma bomba. Mas, nas duas horas seguintes, a fim de reduzir o tempo de esvaziamento, outra bomba foi ligada junto com a primeira. O gráfico, formado por dois segmentos de reta, mostra o volume de água presente na cisterna, em função do tempo.
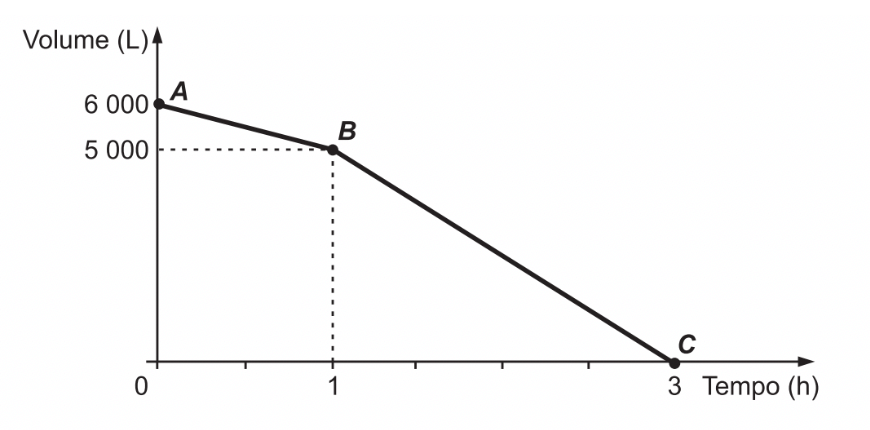
Qual é a vazão, em litro por hora, da bomba que foi ligada no início da segunda hora?
a) 1 000
b) 1 250
c) 1 500
d) 2 000
e) 2 500
2) (UERJ) Os veículos para transporte de passageiros em determinado município têm vida útil que varia entre 4 e 6 anos, dependendo do tipo de veículo. Nos gráficos está representada a desvalorização de quatro desses veículos ao longo dos anos, a partir de sua compra na fábrica.
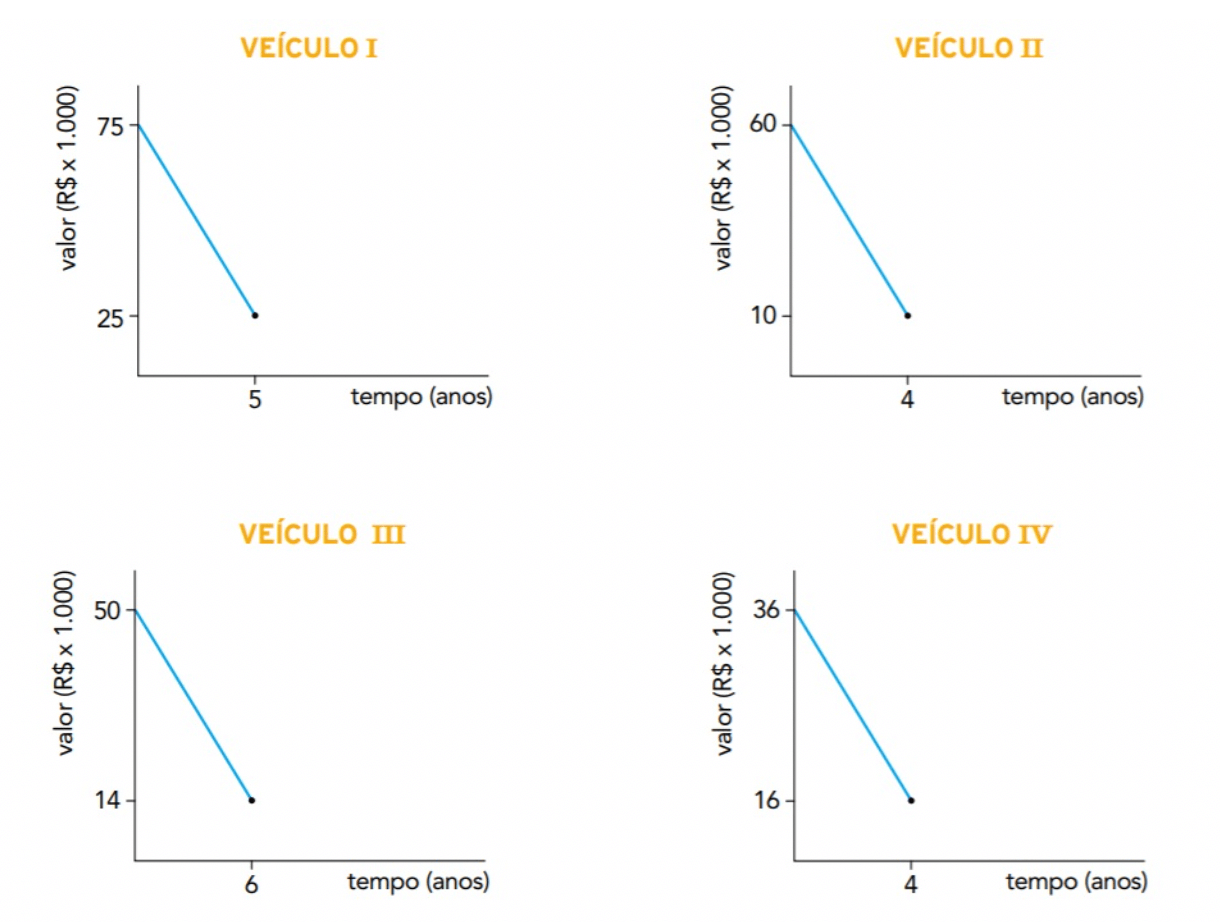
Com base nos gráficos, o veículo que mais desvalorizou por ano foi:
a) I
b) II
c) III
d) IV
Bem tranquilo, não é? Se você gostou desta abordagem, clique aqui para saber como a Plataforma do Professor Ferretto funciona!
Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!
E agora, para fecharmos o assunto com chave de ouro, deixo um vídeo que aborda o coeficiente angular. Nele, vocês também conferem tudo sobre o coeficiente linear da função afim. Assistam este vídeo e eu garanto: não restará mais nenhuma dúvida sobre a construção da função do primeiro grau!
Um abraço! Vejo vocês no próximo post!