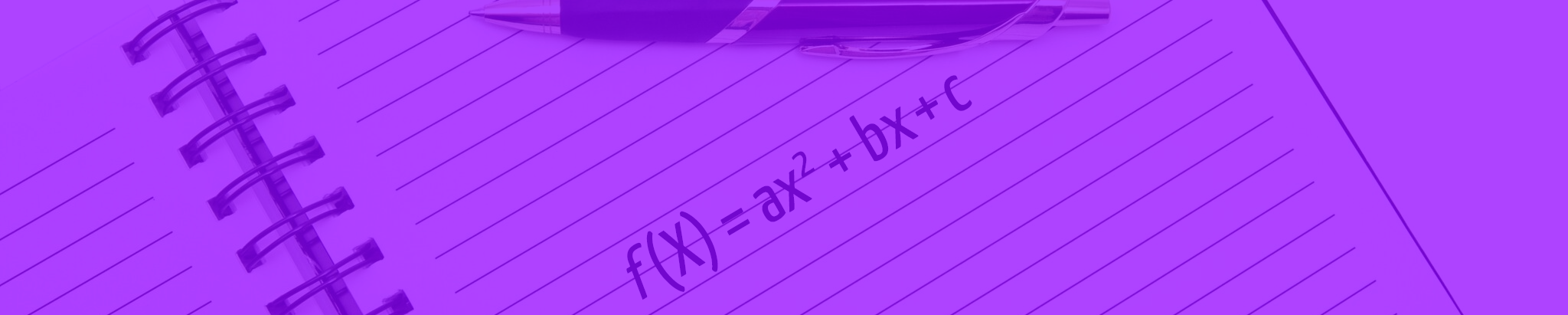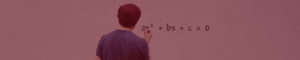FÓRMULA DE BHASKARA
20/03/2020
A fórmula de Bhaskara é uma das fórmulas mais conhecidas dentro da matemática. Ela é utilizada para determinar as raízes das equações do segundo grau, principalmente quando estas equações estão em seu formato completo, ax2 + bx + c = 0. No mundo todo, a fórmula de Bhaskara é conhecida como fórmula quadrática.
Olá, pessoal! Tudo tranquilo?
No texto de hoje, nós vamos estudar uma das fórmulas mais conhecidas dentro de toda a matemática. Tenho certeza que só de ouvir falar em “fórmula de Bhaskara”, vocês conseguem descrevê-la mentalmente, não é? Mas qual será a história dessa fórmula? Por que se chama fórmula de Bhaskara? Como essa fórmula foi deduzida? Onde ela é utilizada? Vamos responder todas essas perguntas logo mais!
Feito, pessoal?! Então, para quem ainda não conhece, essa é a fórmula de Bhaskara!
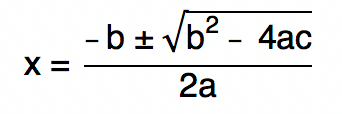
Vamos começar nosso estudo entendendo um pouquinho da história dessa fórmula e a sua relação com o matemático Bhaskara Akaria. Vem comigo!
1. BREVE HISTÓRIA DA FÓRMULA DE BHASKARA

Quando nos deparamos com a expressão “Fórmula de Bhaskara”, a conclusão mais óbvia parece ser a de que Bhaskara Akaria, um professor, astrólogo, astrônomo e matemático indiano descobriu a fórmula. Contudo, não foi exatamente isso que aconteceu.
Existem registros da existência da fórmula de Bhaskara em textos escritos por babilônios cerca de 4000 anos antes da própria existência de Bhaskara. Nestes textos, é claro, a fórmula não era descrita da forma como a conhecemos hoje, com os coeficientes a, b e c e a incógnita x. Naquela época, a álgebra ainda não existia, por isso, as fórmulas eram apresentadas através de regras, que nada mais eram do que descrições por extenso em forma de poesia, que listavam as operações necessárias para resolver alguns problemas específicos.
O fato é que somente por volta de 400 anos depois que Bhaskara viveu, um matemático francês chamado François Viète se dedicou a obter uma fórmula algébrica baseada nas descrições que existiam. Desde então, é que temos a disposição a fórmula estrela do texto de hoje.
1.1 Então, por que ainda chamamos a fórmula de “Fórmula de Bhaskara”?

Bhaskara escreveu alguns livros durante sua trajetória como matemático. Em um desses livros, ele cita as regras que deram origem fórmula “de Bhaskara” que conhecemos hoje. Por isso, acredita-se que em algum momento da história da matemática brasileira, algum autor analisou a obra de Bhaskara e atribuiu esse nome a fórmula.
Incrível, não é, pessoal? Agora, nós vamos descobrir onde a fórmula de Bhaskara é aplicada. Sigam comigo!
2. A FÓRMULA DE BHASKARA E AS EQUAÇÕES DO 2º GRAU
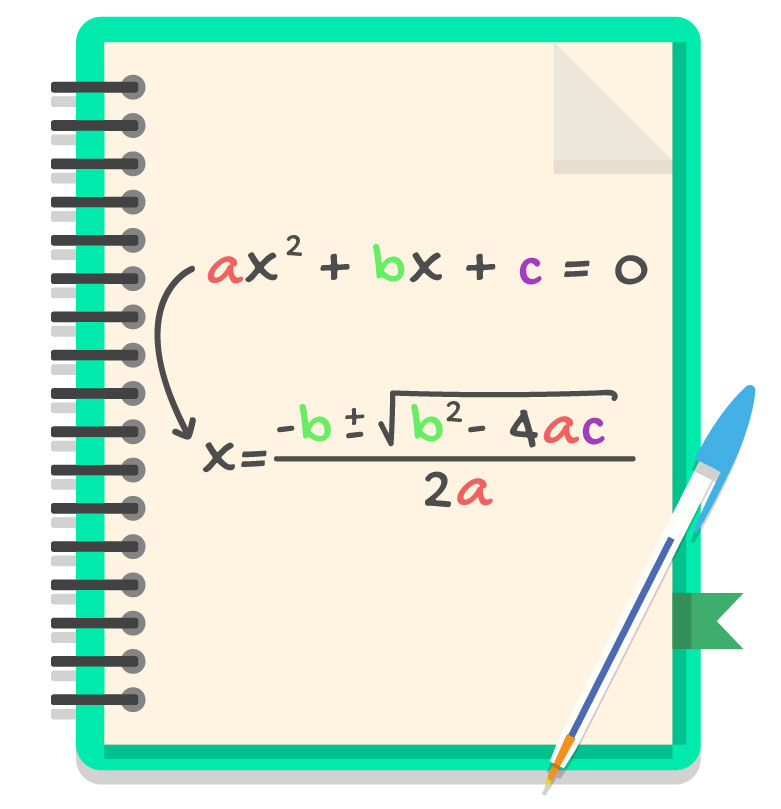
A fórmula de Bhaskara é utilizada para resolver as equações do 2º grau, ou seja, para encontrar as raízes da equação, tendo por base apenas os valores dos coeficientes a, b e c. Como a imagem acima sugere, para encontrarmos as raízes de uma equação do segundo grau, basta substituirmos os valores numéricos dos coeficientes a, b e c na fórmula de Bhaskara, realizar as operações propostas por ela, e ao fim, teremos os valores desejados.
As raízes da equação do 2º grau costumam ser chamadas de x1 e x2, ou então, de x’ e x” e são sempre duas. Por isso, temos o sinal ± na fórmula de Bhaskara. Para encontrar o valor da raiz x1 ou x’, deve-se utilizar um dos sinais, por exemplo, o sinal positivo. Para encontrar o valor da raiz x2 ou x”, basta utilizar o outro sinal, neste exemplo, o sinal negativo.
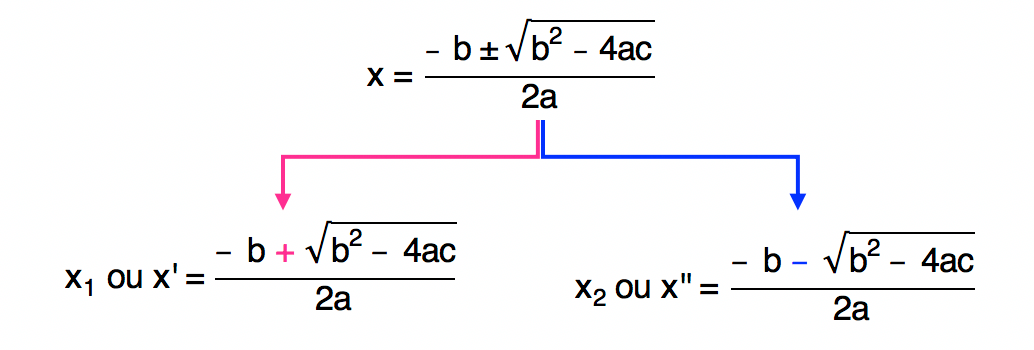
É muito importante que fique claro que não existe uma ordem específica para a distinção do sinal ± entre as raízes da equação do 2º grau. Poderíamos, sem problema algum, encontrar a raiz x1 ou x’ com o sinal negativo e a raiz x2 ou x” através do sinal positivo. Vocês decidem o que funciona melhor para vocês!
Algumas bibliografias apresentam a fórmula de Bhaskara de uma forma diferente desta que acabamos de conhecer. Isso porque alguns termos da fórmula trazem detalhes muito interessantes sobre as raízes das equações do 2º grau. Vamos conhecer essa variação da fórmula no próximo item. Vem comigo!
2.1 O discriminante da função quadrática na fórmula de Bhaskara
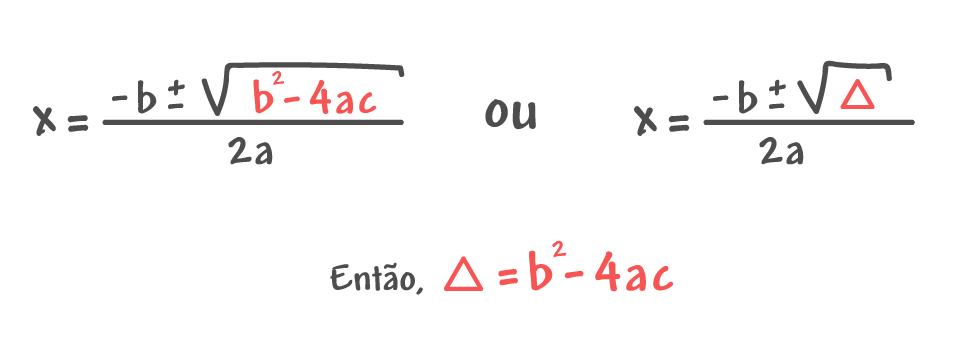
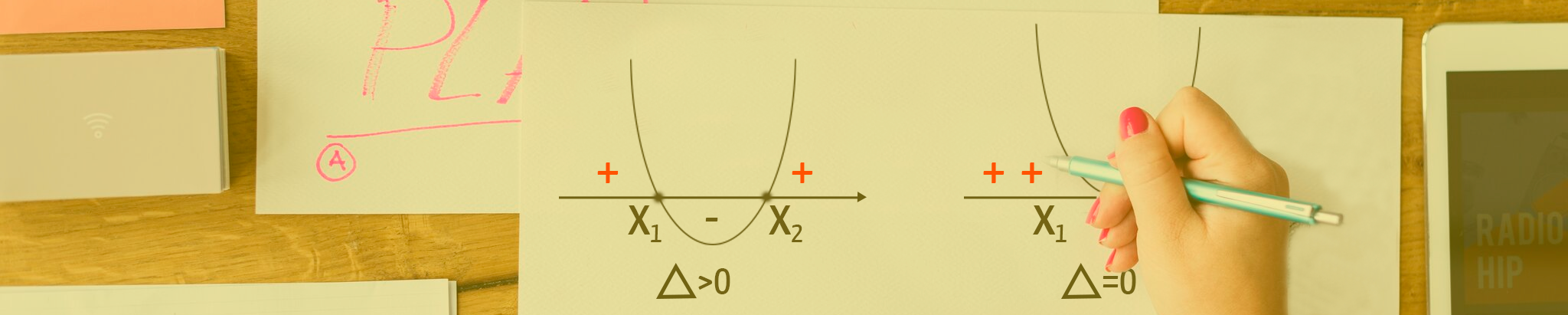
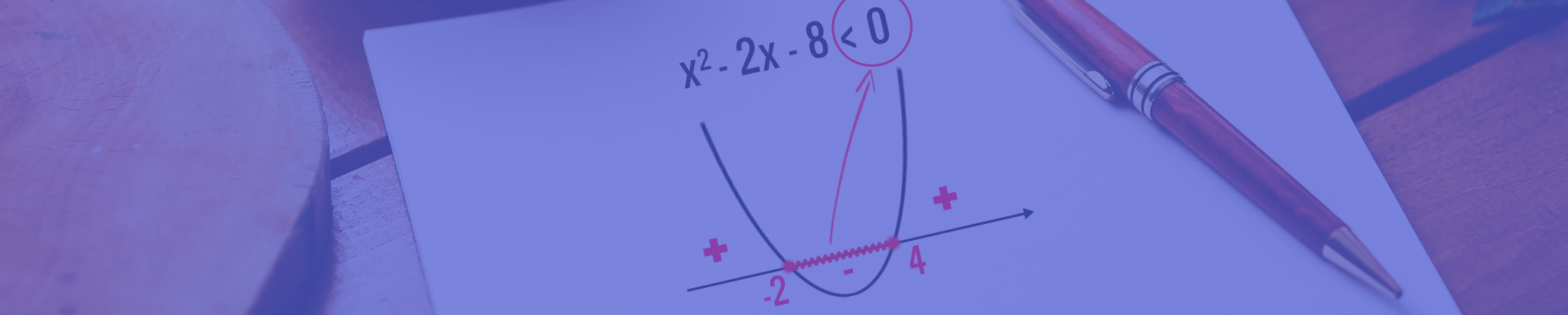
O valor numérico resultante da expressão “b2 – 4ac” representa o chamado discriminante da função quadrática (∆). Através deste valor, é possível determinar se a equação do 2º grau possui duas raízes reais e distintas (∆ > 0), duas raízes reais e iguais (∆ = 0), ou ainda, duas raízes complexas (∆ < 0).
Tendo isso em vista, pode ser mais interessante calcular o valor do delta (∆) ou discriminante da equação, verificar a natureza de suas raízes, e caso elas sejam reais e iguais ou reais e distintas, dá-se sequência ao cálculo da fórmula de Bhaskara a fim de obter o valor numérico das raízes. Vamos utilizar esse método para resolver algumas equações do 2º grau logo mais!
Dúvidas sobre o discriminante e as raízes da função quadrática? Então, clique aqui e vem comigo!
A fórmula de Bhaskara pode ser utilizada para resolver qualquer tipo de equação do 2º grau, seja ela completa (com a, b e c diferentes de zero) ou incompleta (com a ≠ 0, e b ou c ou ambos iguais a zero). Mas, as equações incompletas podem ser resolvidas de uma forma ainda mais simples. Clique aqui para saber tudo sobre as equações do segundo grau incompletas!
3. EQUAÇÕES DO SEGUNDO GRAU RESOLVIDAS

Na sequência, nós vamos resolver juntos cinco equações do 2º grau. Faremos o cálculo do delta (∆) ou discriminante, e dependendo do valor encontrado, seguiremos o cálculo utilizando a fórmula de Bhaskara. Acompanhem comigo!
Equação 1
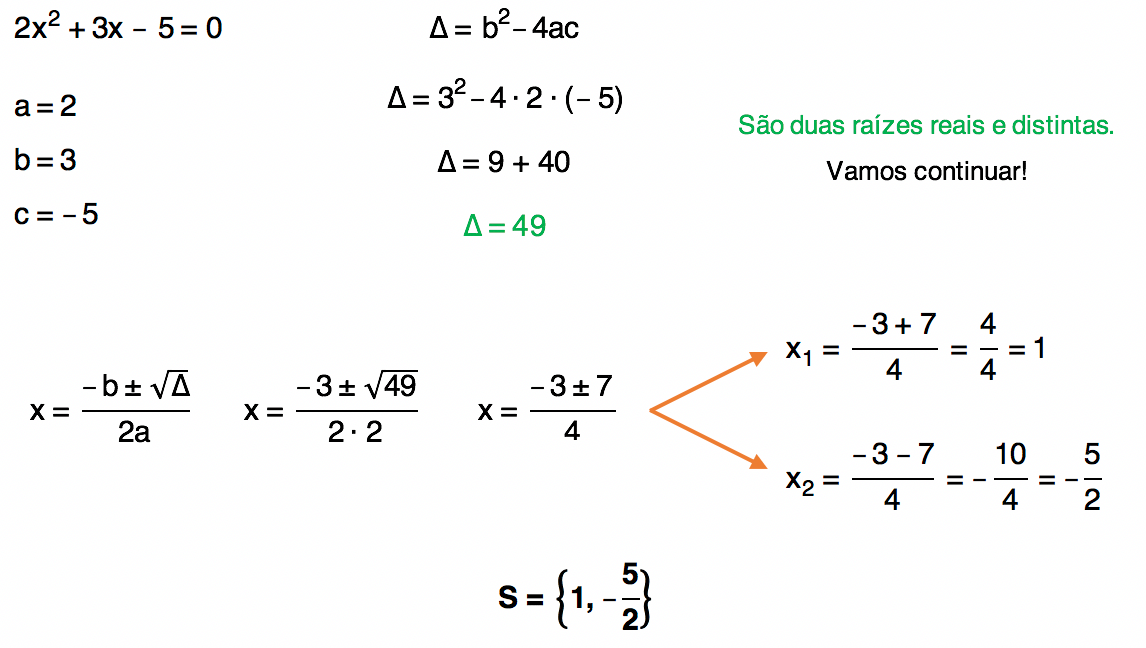
Equação 2
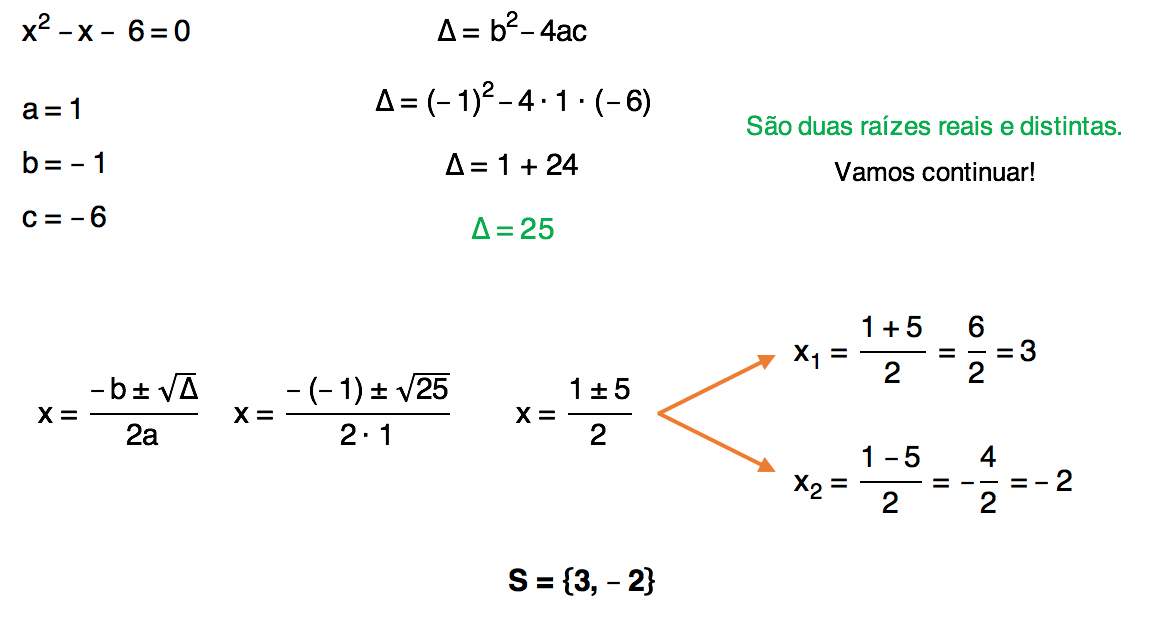
Equação 3
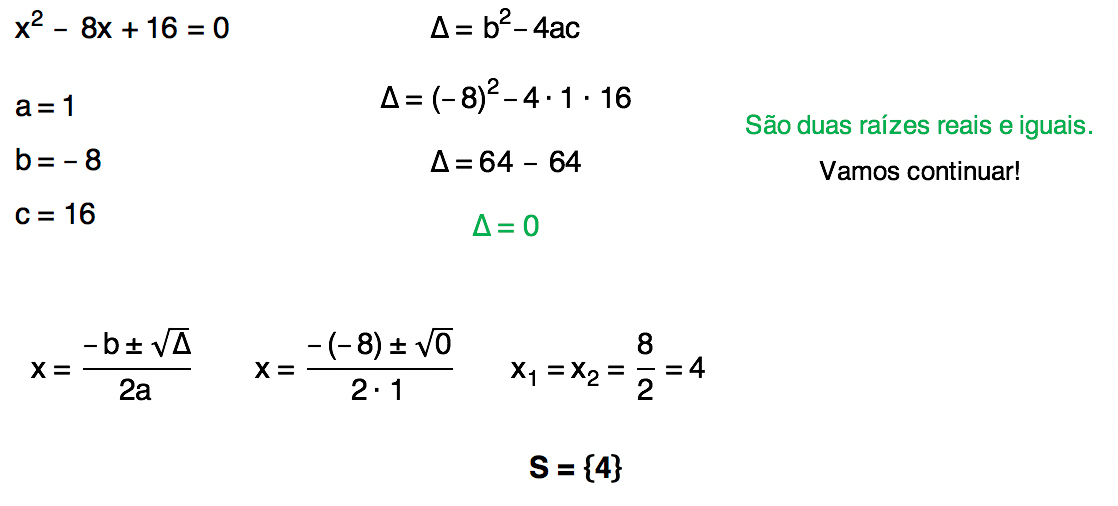
Equação 4
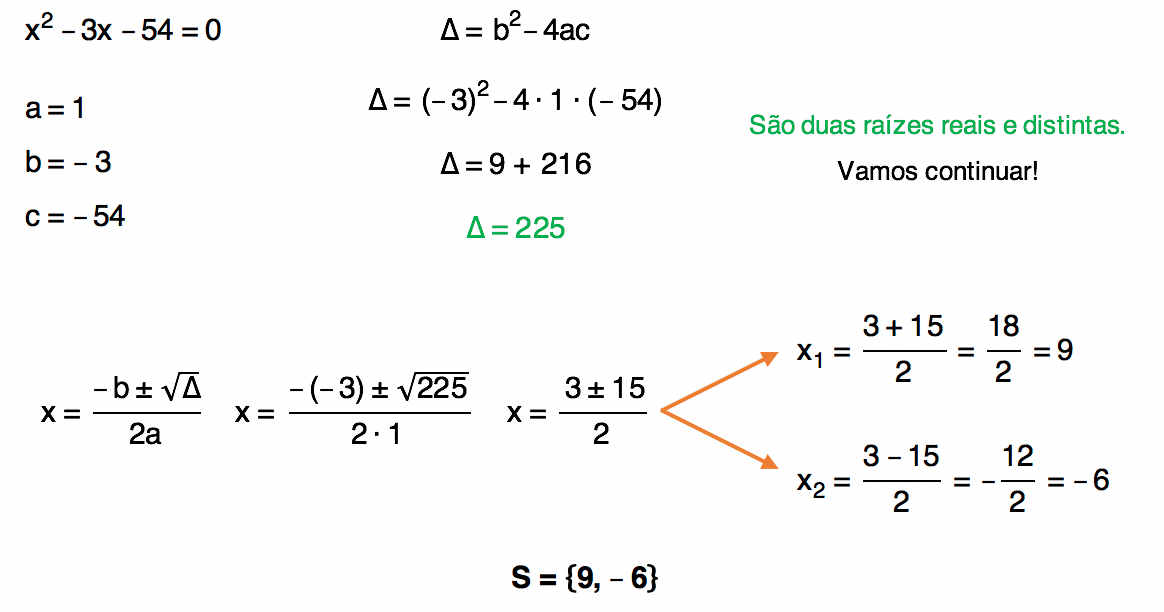
Equação 5
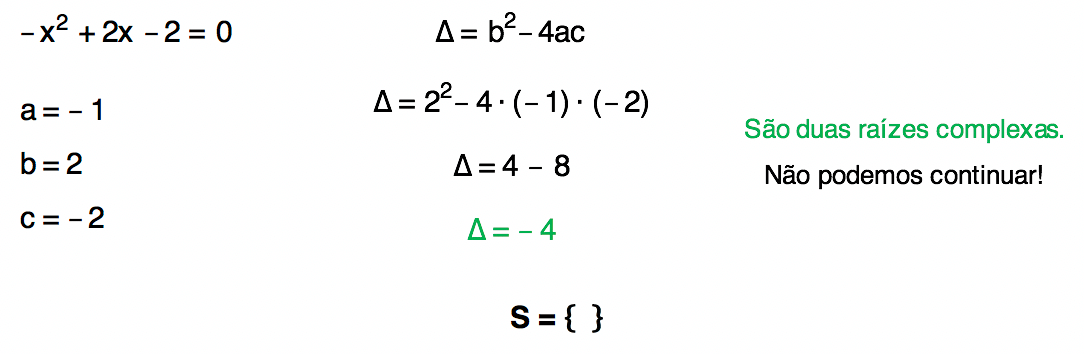
Tranquilo, não é, pessoal? O cálculo do discriminante e a natureza das raízes da equação do segundo grau são estudados aqui no blog. Se vocês não compreenderam por que resolvemos as equações dos exemplos desta forma, cliquem aqui! O blog está cheinho de conteúdo sobre a função quadrática.
4. DEDUÇÃO DA FÓRMULA DE BHASKARA

Nós acabamos de aprender que a fórmula de Bhaskara é um cálculo utilizado para encontrar as raízes da equação do 2º grau. É necessário utilizar a fórmula, pois, do contrário, não conseguimos isolar a incógnita x da equação, como fazemos nas equações do primeiro grau. Analisando a dedução da fórmula de Bhaskara, podemos compreender por que ela pode ser utilizada para esse fim. Acompanhem comigo!
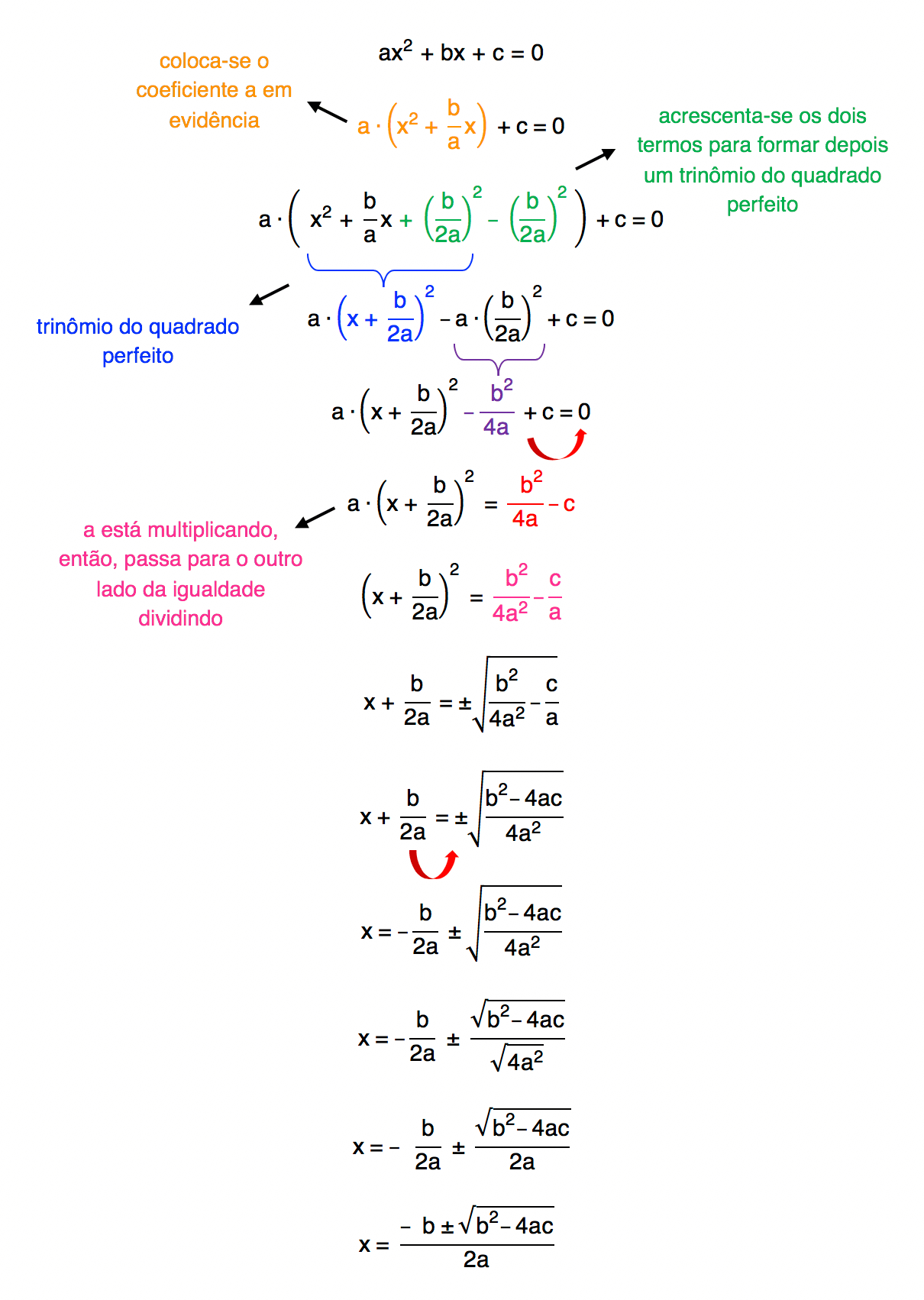
A fórmula de Bhaskara nada mais é do que uma forma de isolar a incógnita x da equação do 2º grau. Reparem que o ponto de partida da dedução da fórmula é a própria equação do 2º grau, e na sequência, são utilizados artifícios matemáticos a fim de isolar a incógnita x. Durante o desenvolvimento desta dedução, alguns passos estão em destaque, para facilitar o entendimento. Mas não se preocupem em memorizar tudo isso, pessoal! Fica a título de conhecimento para vocês.
E assim, estamos prestes a concluir mais um texto. Espero que tudo que vimos aqui tenha sido bastante proveitoso para os estudos de vocês! Quem quiser saber mais sobre as equações do 2º grau, pode ficar à vontade e assistir o vídeo que disponibilizo abaixo. Lá eu mostro detalhes cruciais sobre as resoluções das equações do segundo grau.
Gostou desse conteúdo? Clique aqui para saber como a Plataforma do Professor Ferretto funciona!
Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da Plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!
Um abraço, pessoal! Bons estudos aí!