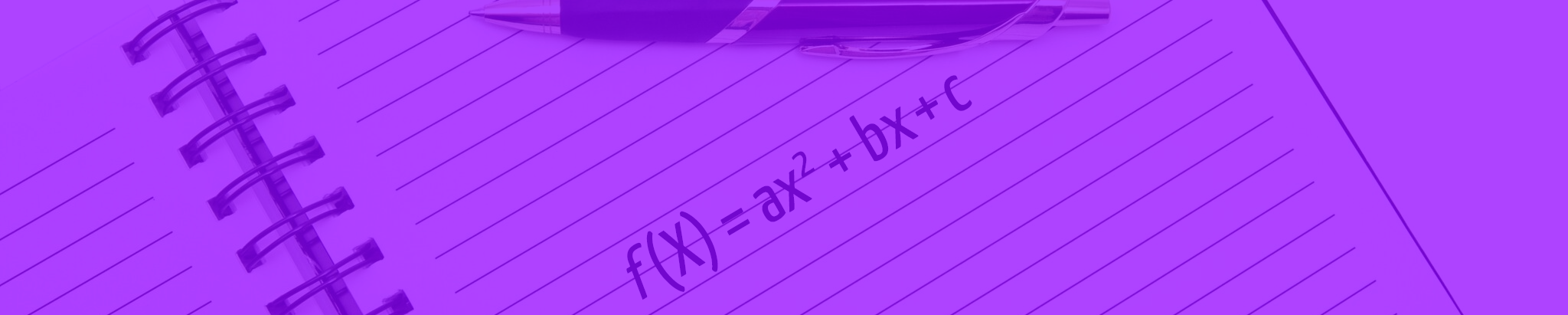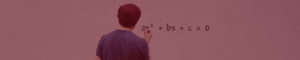COMO ENCONTRAR AS COORDENADAS DO VÉRTICE DA PARÁBOLA?
05/12/2019
O vértice da parábola é o ponto de máximo absoluto ou o ponto de mínimo absoluto do gráfico da função quadrática. É possível determinar as coordenadas do vértice através de fórmulas conhecidas, ou ainda, considerando a simetria da parábola.
Olá, pessoal! Tudo bem?
Hoje é dia de estudarmos um dos pontos notáveis do gráfico da função quadrática: o vértice da parábola. Existem diversas situações do cotidiano que podem ser representadas por gráficos com comportamento semelhante ao da função do 2º grau. Nesses casos, conhecer o ponto em que a função atinge o seu maior ou o seu menor valor pode ser essencial. Sem problema algum, afinal, vocês verão neste texto que é muito simples encontrar o vértice da parábola!
Feito, pessoal? Vamos começar nosso estudo descobrindo como calcular as coordenadas do vértice em si. Em seguida, entenderemos quando essas coordenadas representam um ponto de máximo e quando se referem a um ponto de mínimo. Acompanhem tudo comigo!
1. UTILIZANDO FÓRMULAS CONHECIDAS
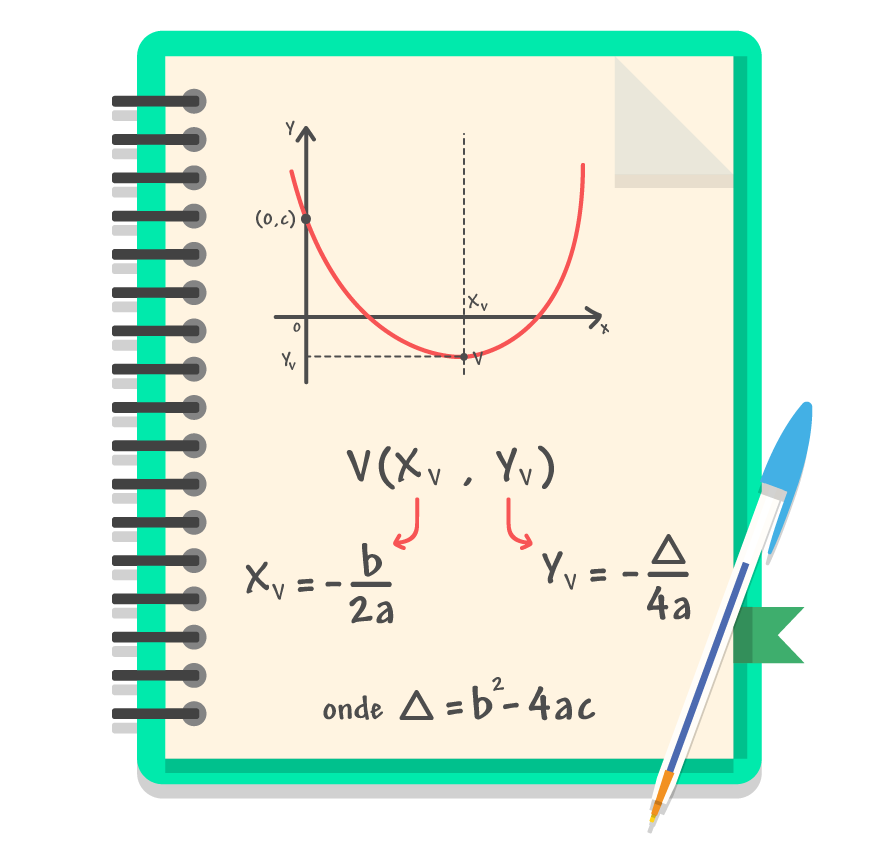
Nós já estudamos no texto Introdução a Função Quadrática que a forma característica da função do 2º grau é f(x) = ax² + bx + c, com a ≠ 0. “a” é o coeficiente do termo x2, e, portanto, não pode ser zero, ou a existência da função estaria comprometida. Enquanto isso, “b” é o coeficiente do termo x, e “c” é o termo independente da função.
Além disso, quem já estudou a natureza das raízes da função quadrática, sabe que para definir se uma função do segundo grau possui duas raízes reais e distintas, duas raízes reais e iguais ou duas raízes imaginárias, é necessário realizar o cálculo do discriminante, ou delta (∆). O valor do delta pode ser calculado através da expressão que se encontra dentro da raiz quadrada da fórmula de Bhaskara, vejam só:
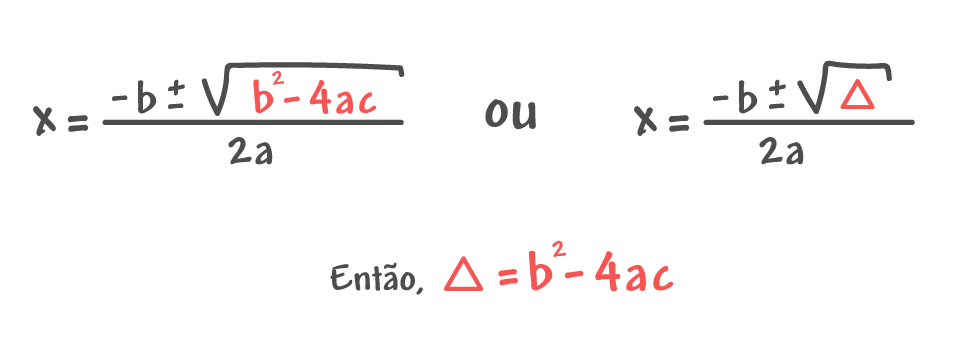
Agora, com toda a certeza, nós já sabemos onde encontrar cada um dos elementos apresentados nas fórmulas das coordenadas do vértice. Portanto, temos plenas condições de calcular as coordenadas dos vértices de algumas funções. É isso que faremos no próximo item, vem comigo!
1.1 Exemplo Resolvido

Dadas as seguintes funções, obtenha as coordenadas de seus vértices:
a. f(x) = –x2 + 4x + 5
Vamos começar definindo o valor dos coeficientes a, b, c, e calculando o valor do ∆ da função:
a = – 1
b = 4
c = 5
∆ = b2 – 4ac
∆ = 42 – 4・(– 1)・5
∆ = 16 + 20
∆ = 36
Pronto! Agora é só substituir os valores encontrados nas fórmulas das coordenadas do vértice:
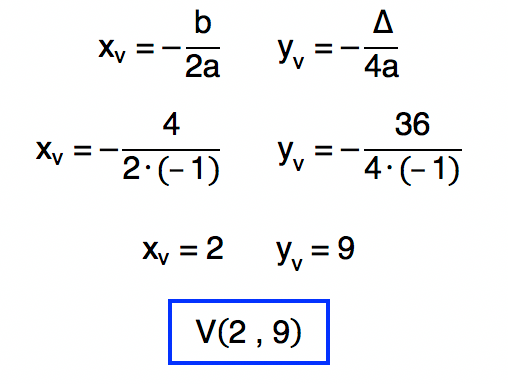
Bem tranquilo, não é? Então vamos a mais um exemplo!
b. f(x) = x2 – 10x + 25
a = 1
b = – 10
c = 25
∆ = b2 – 4ac
∆ = (– 10)2 – 4・1・25
∆ = 100 – 100
∆ = 0

E aí, o que acharam deste último resultado? Apesar de parecer estranho, não tem nada de errado com o valor zero em uma ou nas duas coordenadas do vértice. Daqui a pouco falaremos mais sobre isso. Sigam comigo!
2. PENSANDO NA SIMETRIA DA PARÁBOLA
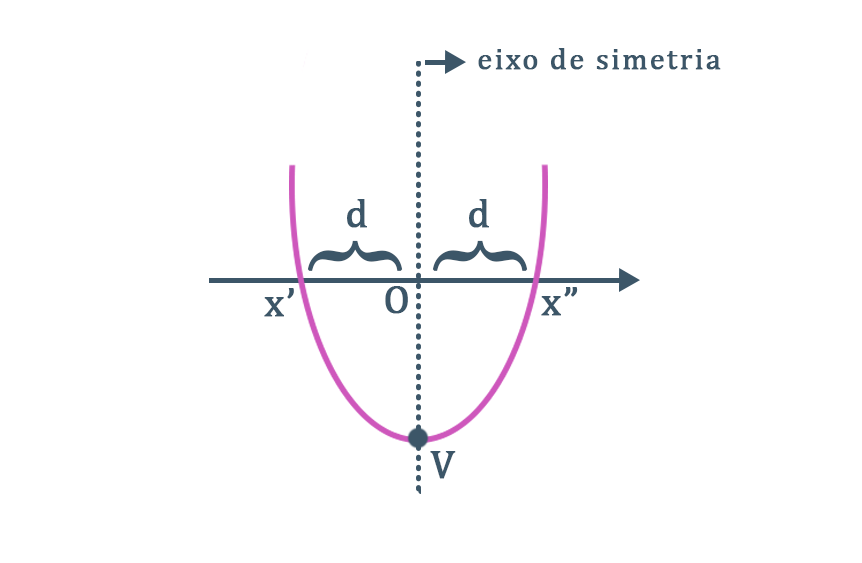
Dada uma função polinomial do segundo grau f(x) = ax² + bx + c, em que a ≠ 0, o seu gráfico sempre será simétrico em relação a um eixo de simetria, que pode ser o eixo y, ou uma reta paralela a este eixo. Reparem na imagem acima, que o tal eixo de simetria passa pelo vértice da parábola e intercepta o eixo x em um ponto O equidistante das raízes x’ e x”.
Dessa forma, é possível concluir que a coordenada xv da parábola está localizada no ponto médio entre as duas raízes da função. Assim, o seu valor numérico pode ser obtido através do cálculo da média aritmética entre as raízes x’ e x”.
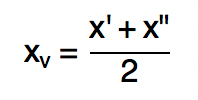
Depois de encontrar a coordenada xv, também é possível encontrar o valor da coordenada yv sem utilizar a fórmula que foi apresentada anteriormente. Para isso, basta calcular o valor da função no ponto xv, substituindo a variável x da função pelo valor numérico de xv.
![]()
Mas afinal, será que esse novo método é mesmo mais simples que o anterior? O jeito é testarmos com alguns exemplos. Vem comigo!
2.1 Exercício Resolvido

Dadas as funções quadráticas abaixo e seus respectivos gráficos, obtenha as coordenadas dos vértices das parábolas.
a. f(x) = x2 + 5x + 4
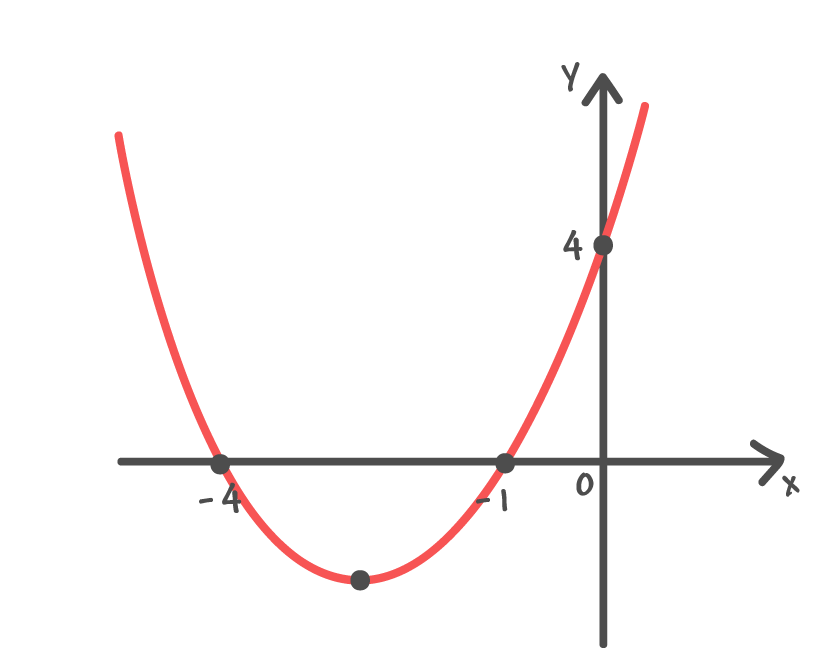
Através do gráfico, é possível compreender que as raízes da função f(x) = x2 + 5x + 4 são x’= – 4 e x” = – 1. Assim, chegamos ao seguinte valor para xv:
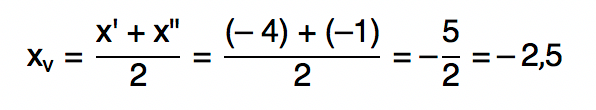
Agora, substituindo a variável x da função f(x) = x2 + 5x + 4 por – 5/2, podemos encontrar o valor da coordenada yv:
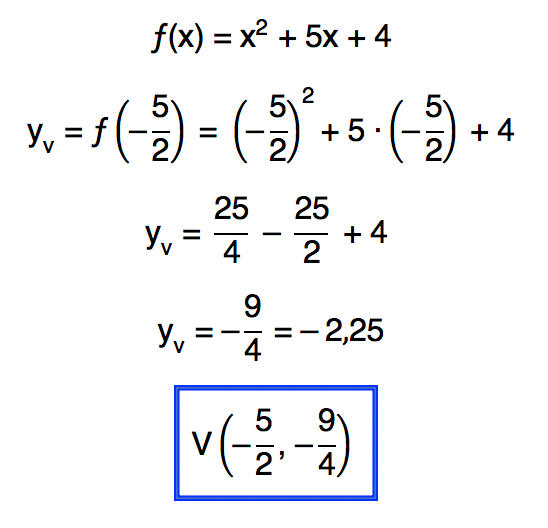
Incrível, não é mesmo? No próximo item, seguiremos a mesma lógica, acompanhem!
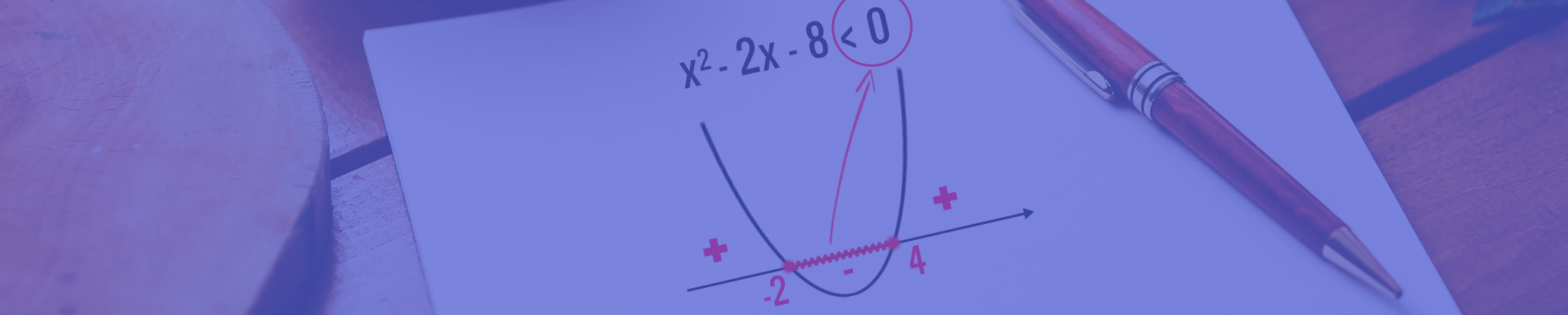
b. f(x) = – x2 – 2x + 8
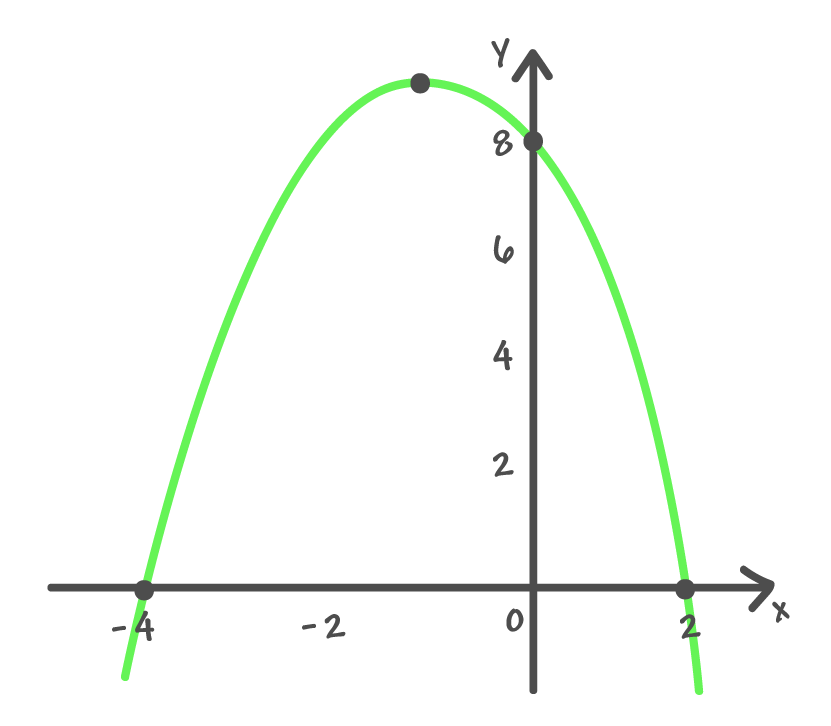
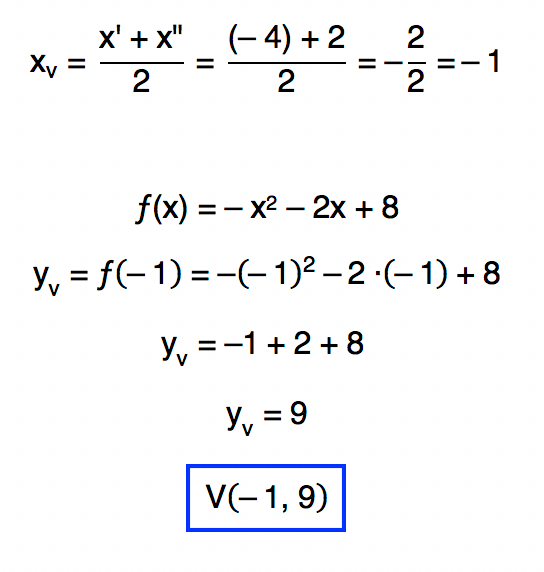

Então, pessoal, caso as raízes de uma certa função quadrática não pertençam ao conjunto dos números reais, o jeito é calcular as coordenadas do vértice através das fórmulas que conhecemos no primeiro item deste texto. No entanto, existem outros detalhes no comportamento da função quadrática aos quais vocês devem ficar atentos. Alguns deles, inclusive, permitem encontrar as coordenadas do vértice num piscar de olhos. Acompanhem comigo as super dicas abaixo!
2.2 Dicas ninja do Ferretto

Quando o vértice está localizado sobre o eixo das abscissas V(xv, 0)
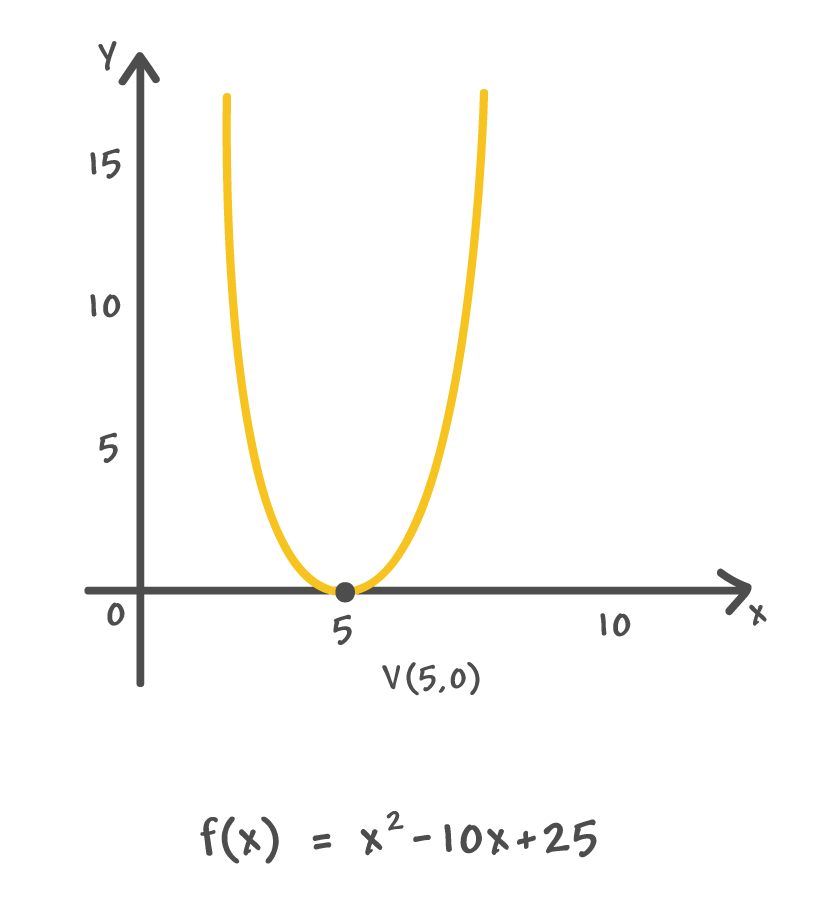
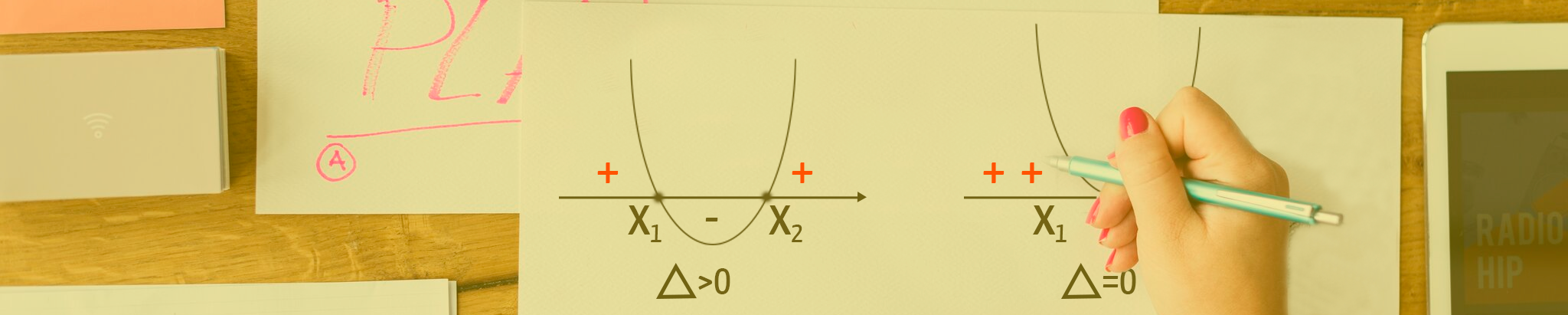
Lembram do delta (∆) que calculamos logo no início do texto, cujo valor era igual a zero? Pois então, quando o discriminante de uma função quadrática é igual a zero, significa que essa função possui duas raízes reais e iguais. Graficamente, isso se traduz em uma parábola que tangencia o eixo x em um único ponto. A coordenada x desse ponto é o valor da raiz da função e também a coordenada xv.
x’ = x” = xv
Quando o vértice está localizado sobre o eixo das ordenadas V(0, yv)
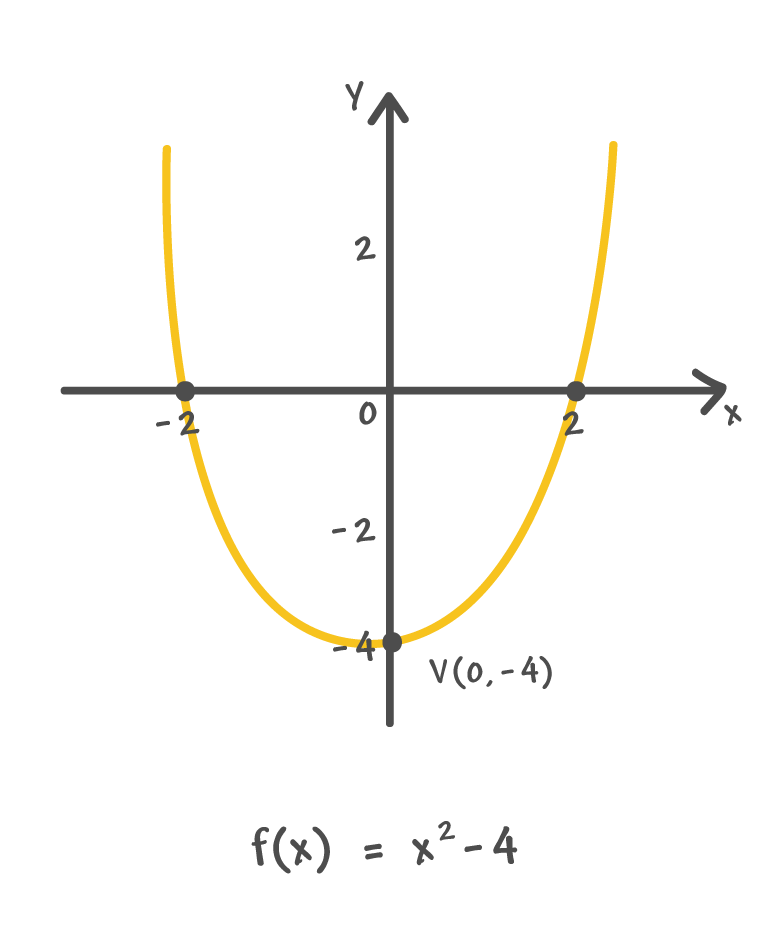
Estamos acostumados a trabalhar com funções quadráticas escritas na forma f(x) = ax² + bx + c, sempre com a ≠ 0. De fato, a não pode ser igual zero, mas os coeficientes b e/ou c podem ser. E quando o coeficiente b de uma função do 2º grau é igual a zero, algo muito interessante acontece: o eixo de simetria da parábola é o próprio eixo y.
Dessa forma, o coeficiente c ou termo independente da função, que representa o ponto onde o gráfico corta o eixo y, representará também o vértice da parábola.
c = yv
Incrível, não é, pessoal? Agora que sabemos tudo sobre as coordenadas do vértice em si, chegou a hora de entendermos quando elas representam um ponto de mínimo e quando representam um ponto de máximo. Sigam comigo!
3. QUANDO O VÉRTICE DA PARÁBOLA É UM PONTO DE MÁXIMO
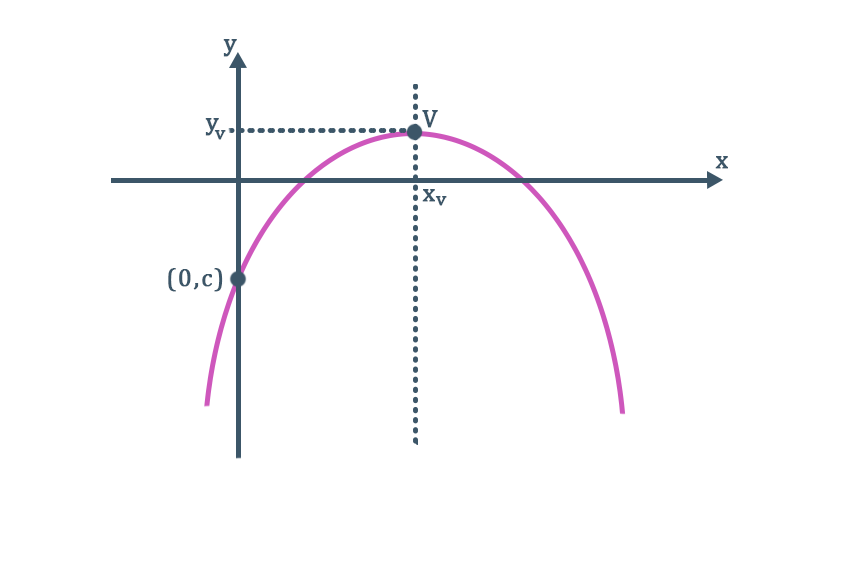
O vértice da parábola é considerado um ponto de máximo quando a concavidade da parábola está voltada para baixo, ou seja, quando o valor do coeficiente a é menor que zero (a < 0). Nesse caso, a coordenada yv representa o valor máximo da função, como podemos ver no gráfico acima.
4. QUANDO O VÉRTICE DA PARÁBOLA É UM PONTO DE MÍNIMO
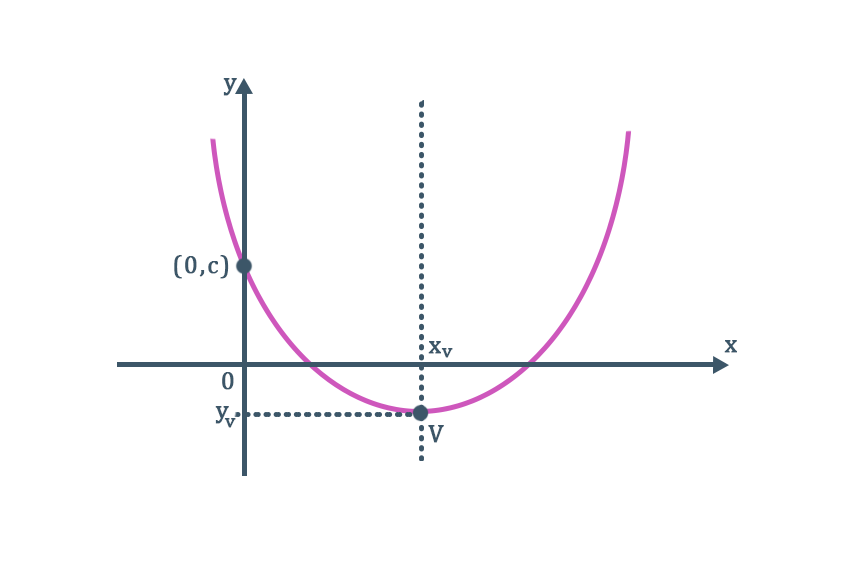
O vértice da parábola é considerado um ponto de mínimo quando a concavidade da parábola está voltada para cima, isto é, quando o valor do coeficiente a é maior que zero (a > 0). Nesse caso, a coordenada yv representa o valor mínimo da função, como também podemos ver no gráfico acima.
5. O VÉRTICE DA PARÁBOLA NO COTIDIANO
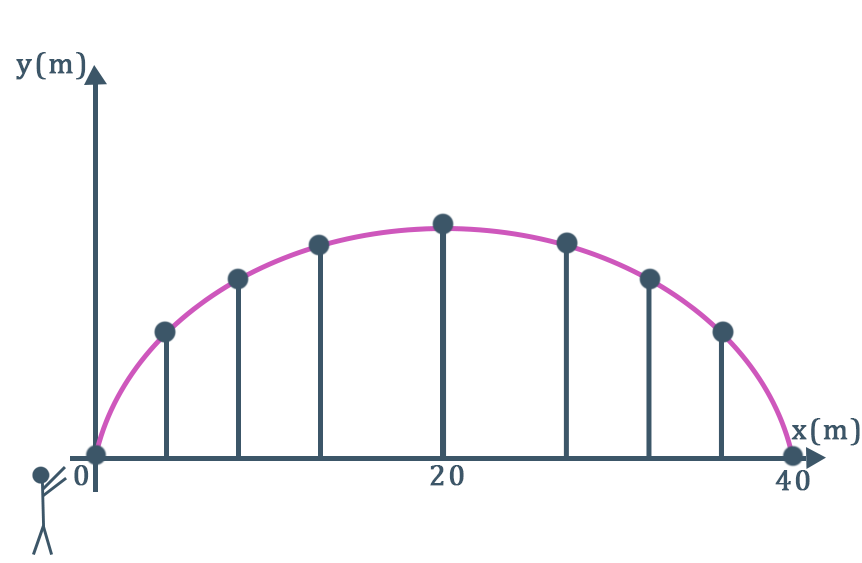
Para que o conceito de valor máximo e mínimo da função quadrática fique mais claro para vocês, vamos a um exemplo prático que envolve o assunto. Imaginem que em um jogo de Basquete interclasses, José fez um lançamento de 40 metros para Henrique marcar uma cesta. Nesse lançamento, a bola descreveu uma parábola como a da imagem acima. A altura em metros atingida pela bola é dada pela função seguinte, na qual x corresponde a distância em metros de onde partiu o passe.
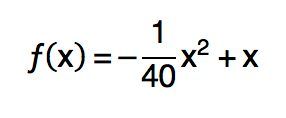
Vejam que após percorrer uma certa distância, a bola atinge sua altura máxima, ou seja, a função possui um ponto de máximo. Esse comportamento pode ser comprovado quando observamos que o coeficiente a da função que descreve a parábola é menor que zero (a < 0). Assim, sem mais delongas, vamos encontrar as coordenadas do vértice da parábola através das fórmulas que estudamos neste texto.
a = – 1/40
b = 1
c = 0
∆ = b2 – 4ac
∆ = 12 – 4・(– 1/40)・0
∆ = 1
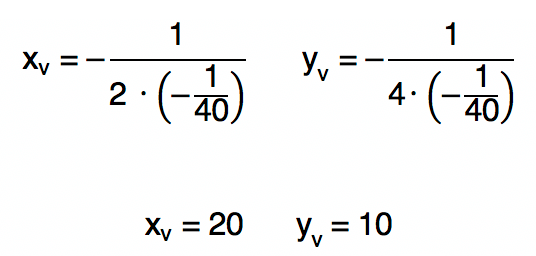
Os valores obtidos nos permitem concluir que após ser lançada e percorrer 20m, a bola atingiu sua altura máxima, que é igual a 10m.
E aí, pessoal, já estão craques no cálculo do vértice da parábola? Entenderam quando este é um ponto de máximo e quando é um ponto de mínimo da função? Então, podemos encerrar o texto com alegria!
Finalizando com chave de ouro!
Espero que tudo o que vimos aqui tenha sido bastante proveitoso! Como de costume, vou deixar em anexo um vídeo sobre o assunto que está repleto de exercícios resolvidos. Assistam o vídeo para praticar bastante o cálculo das coordenadas do vértice da parábola!
Gostou deste conteúdo? Clique aqui para saber como a plataforma do Professor Ferretto funciona!
Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!
Bons estudos e até breve!