INEQUAÇÕES SIMULTÂNEAS DO 2º GRAU
28/11/2018
Olá, pessoal! Tudo bem?
Se duas inequações do 1º grau podem ser resolvidas ao mesmo tempo, por que não poderíamos fazer isso com duas inequações do 2º grau também? Hoje eu vou provar para vocês, com a ajuda de um exemplo bem detalhado, que resolver duas inequações do segundo grau simultaneamente é moleza! Mas para que essa leitura flua bem, é importante que vocês saibam como resolver inequações do 2º grau, e também como realizar o estudo do sinal de uma função quadrática. Não custa nada dar uma olhadinha nesses textos, e depois de vê-los, eu garanto, vai ficar mais fácil de solucionar qualquer questão que envolva o assunto!
E para quem acha que eu estou blefando ao dizer que a matemática é simples, que tal dar uma olhada no curso de matemática 100% online que disponibilizo em minha plataforma? Ter acesso a um material apoio de qualidade, e a videoaulas sobre toda a matemática do ensino médio, garante a preparação completa para as provas do ENEM e dos vestibulares que estão por vir! E se ainda assim restar alguma dúvida, não tem problema, é só contar com a ajuda dos monitores no plano diamante! Querem conhecer todas as vantagens da plataforma do Ferretto? Então acessem já o site!
Beleza, pessoal? Quem leu o texto Inequações Simultâneas do 1º Grau, vai perceber que vamos utilizar o mesmo método para encontrar a solução das inequações simultâneas de grau 2. O primeiro passo consiste em resolver cada umas das inequações apresentadas separadamente, o que gerará duas soluções diferentes. Essas duas soluções ainda não serão o resultado final da operação, afinal, nem todos os valores reais que satisfazem uma das inequações podem necessariamente satisfazer a outra, e vice-versa. Por isso, a fim de garantir que a solução encontrada atenda as duas inequações ao mesmo tempo, nós realizaremos a intersecção dos dois resultados, e aí sim finalmente chegaremos a solução como um todo!
Contudo, não podemos esquecer de um detalhe bem importante: infelizmente, as inequações do segundo grau não são resolvidas da mesma maneira que as inequações de grau 1. Como na maioria das vezes nós não conseguimos isolar a incógnita x das inequações do 2º grau, é necessário transformar a parte esquerda destas desigualdades em uma função do 2º grau! Feito isso, basta estudarmos o seu sinal, e pronto: estarão garantidas as nossas soluções!
É, pessoal, eu sei que em forma de texto fica mais difícil de entender todo o processo. Por isso, chega de ladainha! Vamos partir logo para o exemplo de hoje. Vem comigo aqui!
1. –8 ≤ x2 – 2x – 8 ≤ 0
Como vimos no texto Inequações Simultâneas do 1º Grau, as inequações simultâneas podem mesmo se apresentar do jeitinho que vemos acima: com dois sinais de desigualdade! Se isso acontecer, não se assustem: separem as mesmas em duas, e desta maneira um sistema será formado, como podemos observar na imagem abaixo.
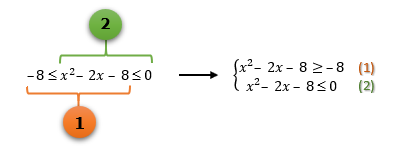
Depois que o sistema é formado, já é possível partirmos para a resolução de cada uma das inequações separadamente, como temos previsto. Contudo, antes de transformamos a parte esquerda de cada desigualdade em uma função, é necessário atentar para o seguinte detalhe:
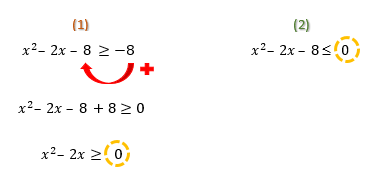
E aí, deu pra perceber alguma semelhança entre a parte direita de ambas as desigualdades? Para que a parte esquerda de uma inequação do segundo grau possa ser transformada em uma função, o lado direito da desigualdade deve, necessariamente, ter apenas o termo zero. Se isso não acontecer de imediato, como vemos na primeira inequação do exemplo, vocês devem tomar medidas para que isso ocorra, ou seja, devem passar os termos que se encontram a direita da inequação para o outro lado, como acabamos de fazer.
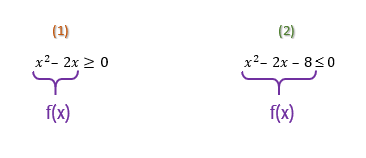
Agora já estamos prontos para estudar o sinal de cada uma dessas funções. E para que esse estudo seja feito com exatidão, vocês podem seguir os seguintes passos:
1. Determinar o valor dos coeficientes a, b, e c de cada função.
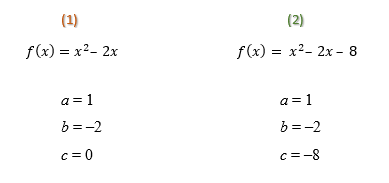
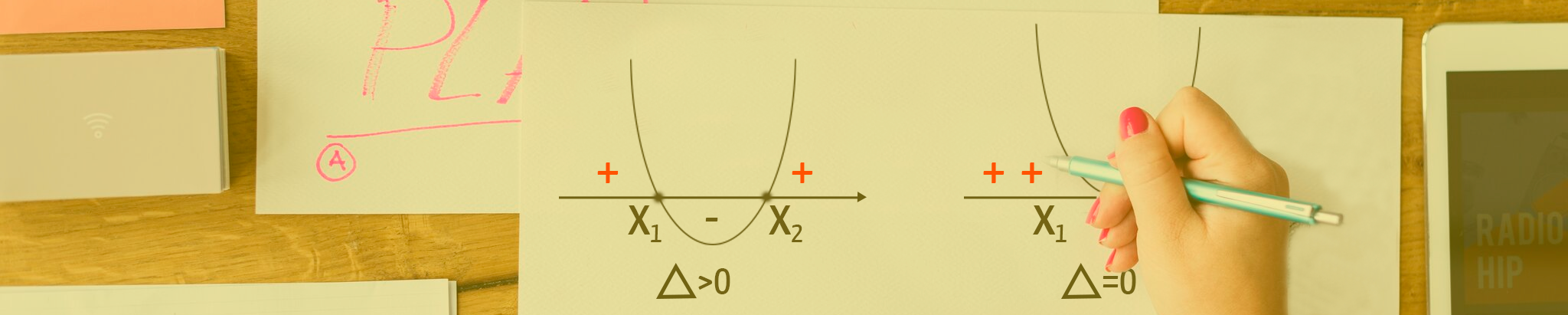
2. Calcular o discriminante (∆) de cada uma das funções.
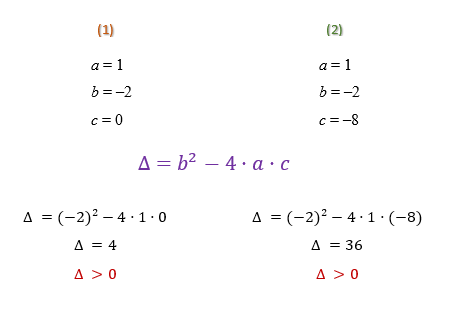
Se o discriminante de uma função quadrática é positivo ou maior que zero, significa que essa função possui duas raízes reais e distintas, ou diferentes. Encontrar os valores numéricos dessas raízes é essencial, afinal, precisaremos deles para esboçar o gráfico de cada função logo mais.
3. Encontrar as raízes das funções através da fórmula de Bhaskara ou do método da soma e produto.
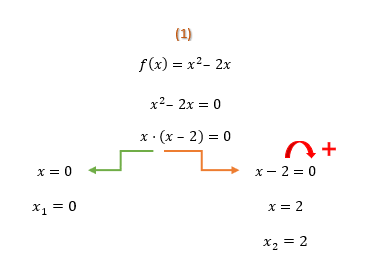

Pessoal, vocês não repararam que a primeira função do 2º grau que formamos é incompleta? Uma função do segundo grau é incompleta, quando qualquer um de seus coeficientes que não seja o a vale zero. Em casos como esse, sempre poderemos evitar o uso da fórmula de Bhaskara e do método da soma e produto, porque conseguimos isolar a incógnita x! Se vocês desejam saber mais sobre o assunto, não deixem de dar uma olhada no texto Equações do 2º Grau Incompletas. Mas se já está tudo entendido, vamos ao cálculo das raízes da nossa segunda função do 2º grau. Nesse caso, não haverá como fugir da famosa fórmula de Bhaskara, olhem só:
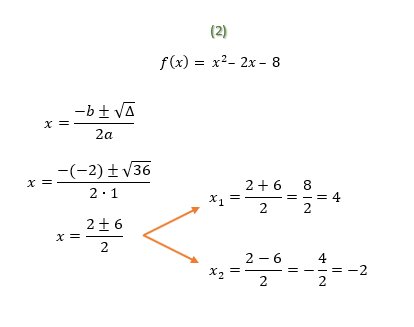
Agora já estamos quase prontos para esboçar o gráfico das duas funções. Temos o valor numérico de suas raízes, contudo, ainda precisamos definir a concavidade de cada uma das parábolas. Como o coeficiente a de ambas as funções vale 1, que é um valor positivo, está definido: a concavidade das duas parábolas é voltada para cima!
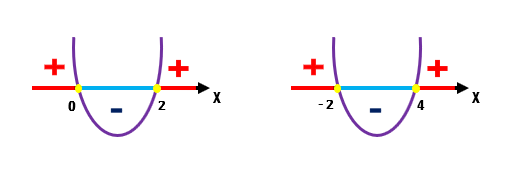
Conhecendo o esboço do gráfico das duas funções, é chegada a hora de voltarmos a dar uma olhada lá nas inequações iniciais que motivaram todo esse passo a passo. O sinal de desigualdade de cada uma delas irá nos informar, se os valores de x que procuramos são aqueles que tornam a função maior do que zero ou positiva, menor do que zero ou negativa, ou mesmo exatamente igual a zero!
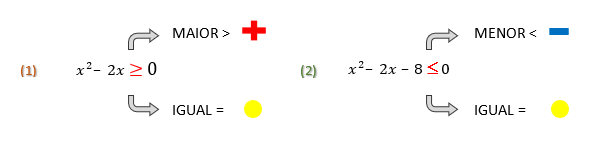
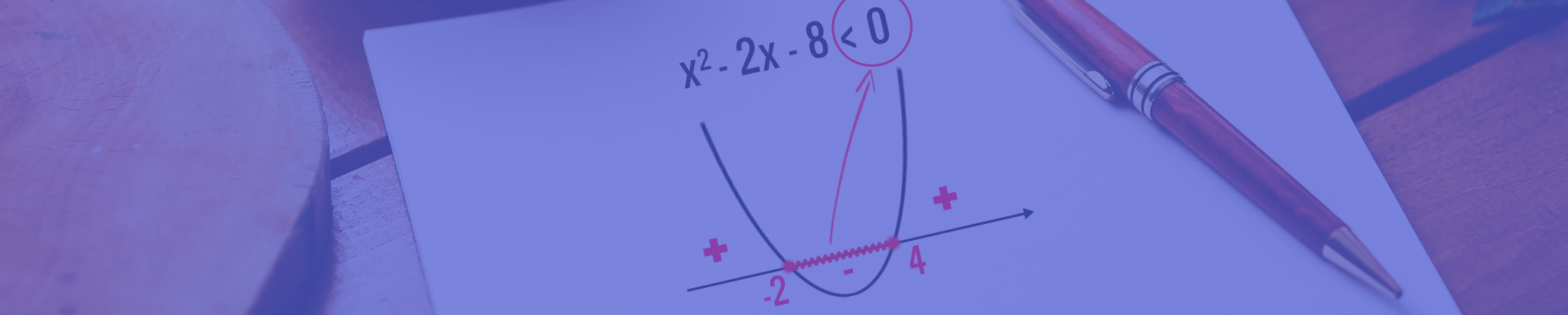
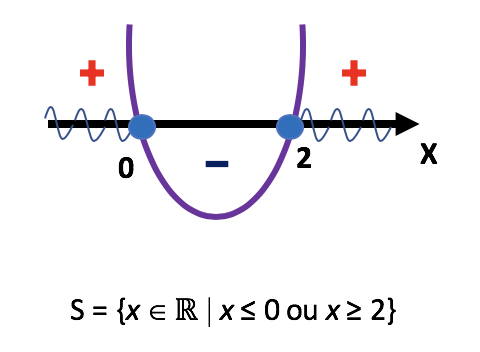
É possível ver na imagem acima, que a solução da primeira inequação será formada pelos valores de x que tornam a função positiva ou igual a zero (sinal de desigualdade ≥). Assim, nos interessam apenas os valores de x menores do que zero e maiores do que 2, afinal, nessas regiões o gráfico se encontra acima do eixo x. Também não podemos deixar de reparar, que as duas raízes da função entrarão na solução, até porque, exatamente nesses pontos o gráfico corta o eixo x, e portanto, torna a função igual a zero.
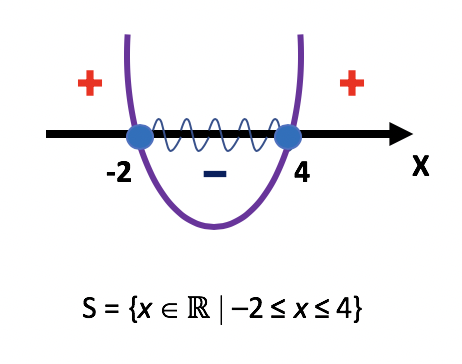
Já em relação a solução da segunda inequação, temos um caso um pouquinho diferente. Através do sinal de desigualdade ≤, fica determinado que apenas os valores de x que tornam a função negativa ou igual a zero satisfazem a inequação. Assim, nos interessam apenas os valores de x que se situam entre –2 e 4, afinal, somente nessa região o gráfico se encontra abaixo do eixo x. Contudo, não podemos negar que as duas raízes da função também farão parte da solução, porque exatamente nesses pontos o gráfico corta o eixo x, e torna a função igual a zero.
Ufa, parece que estamos quase no fim dessa extensa solução! Agora que sabemos os valores de x que satisfazem as duas inequações separadamente, precisamos definir quais deles satisfazem as duas inequações ao mesmo tempo. Então, sem mais delongas, partiu intersecção!
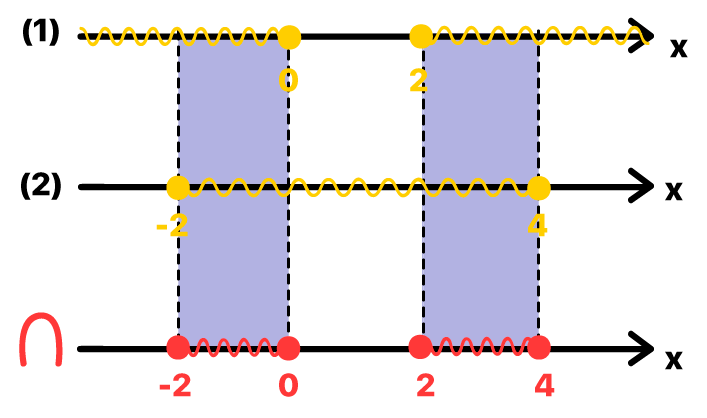
Vejam que desenhamos acima três retas reais, que representam, respectivamente, as soluções da inequação 1, da inequação 2, e por fim, a solução da inequação simultânea como um todo. Reparem que os únicos valores de x que satisfazem ambas as inequações, e portanto, pertencem ao conjunto intersecção, são aqueles que iniciam em –2 e terminam em 0, e também aqueles que iniciam em 2 e terminam em 4, incluindo os próprios –2, 0, 2 e 4, já que todos eles fazem parte de ambas as soluções (bolinha fechada).
S = {x ∈ ℝ | –2 ≤ x ≤ 0 ou 2 ≤ x ≤ 4}
E aí, pessoal, estão cansados? Eu sei, de pequenas, as resoluções das inequações simultâneas do 2º grau não têm nada! Mas espero que vocês tenham entendido o assunto, e que possam utilizar esse exemplo como base para as soluções de vocês! Aproveitem que o texto está terminando, e deem uma olhada também no vídeo que está em anexo! Lá vocês conferem mais alguns exemplos resolvidos, e claro, aquelas dicas do Ferretto sobre as funções quadráticas e tudo que envolve o assunto!
Um abração a todos!