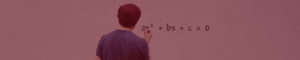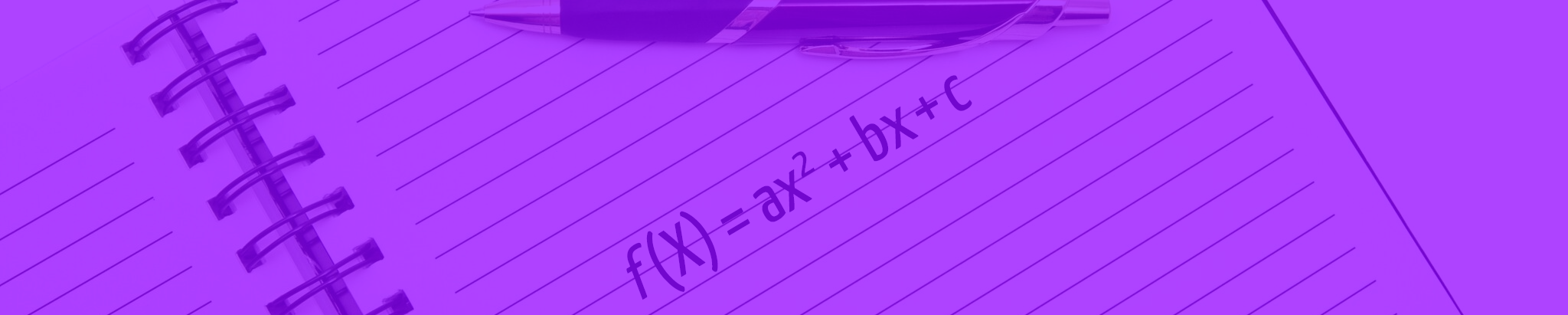As equações do 2º grau incompletas, dadas na forma ax² + bx + c = 0, são aquelas em que pelo menos um dos coeficientes, que não aquele que acompanha o termo x², é de valor zero. Quando as equações do 2º grau são incompletas, é possível isolar a incógnita x, o que facilita, e muito, a resolução deste tipo de equação.

 

Olá, pessoal! Como vão?

Hoje nós vamos estudar as equações do 2º grau incompletas, aquelas que podem ser resolvidas sem o uso da fórmula de Bhaskara ou do método da soma e produto.  Basicamente, existem 3 tipos de equações do segundo grau incompletas, cujas raízes possuem um comportamento definido. Por isso, quem está se preparando para as provas do ENEM e dos vestibulares não pode perder este texto! Vamos aprender a resolver cada uma dessas equações junto a uma série de exemplos.

Legal, não é mesmo? Então, não esqueçam de anotar todos os conceitos importantes que veremos logo mais. Peguem seus materiais de estudo e sigam comigo!

 

1. O QUE É UMA EQUAÇÃO DO 2º GRAU INCOMPLETA?

O formato das equações do segundo grau é o famoso “ax² + bx + c = 0”, em que a, o coeficiente que acompanha o termo x², jamais pode ser zero. Quando a, b e c são valores reais diferentes de zero, diz-se que a equação do 2º grau formada é completa. Mas quando a é diferente de zero (e deve ser!) e b ou c ou ambos os coeficientes são iguais a zero, dizemos que a equação gerada é incompleta.

ax² = 0 → Quando os coeficientes b e c são iguais a zero

ax² + c = 0 → Quando o coeficiente b é igual a zero

ax² + bx = 0 → Quando o coeficiente c é igual a zero

Você sabe por que o coeficiente a da equação do 2º grau não pode ser igual a zero? Não? Então clique aqui.

Podemos resolver as equações do 2º grau incompletas da mesma forma que resolvemos as equações completas, ou seja, através da fórmula de Bhaskara ou do método da soma e produto. Contudo, existe uma maneira ainda mais simples de resolver esse tipo de equação. No próximo item, vamos entender qual é essa maneira e porque é possível fazer uso dela. Vem comigo!

 

2. POR QUE NÃO É NECESSÁRIO UTILIZAR A FÓRMULA DE BHASKARA PARA RESOLVER AS EQUAÇÕES DO 2º GRAU INCOMPLETAS?

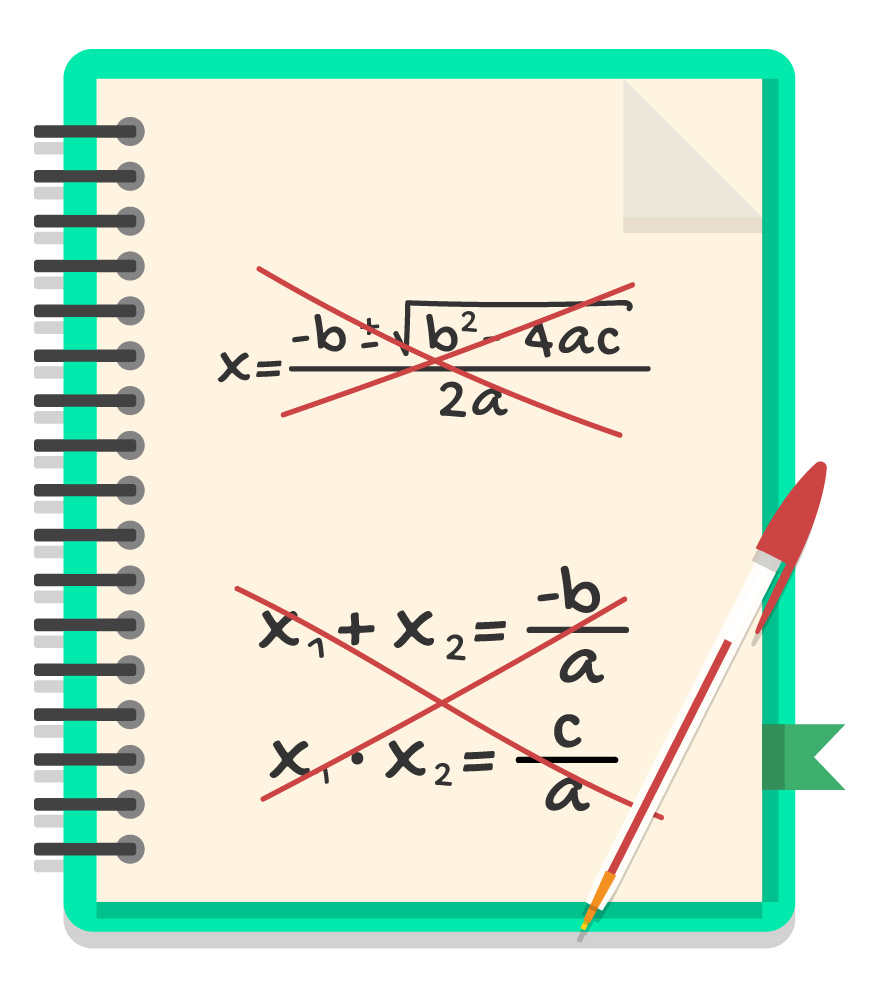
Para entendermos porque é possível fugir da fórmula de Bhaskara e até do método da soma e produto para resolver as equações do 2º grau incompletas, vamos trazer à tona uma outra equação muito importante para a matemática: a equação do 1º grau.

3x – 6 = 0

3x = 6

x = 6/3

x = 2

Reparem no exemplo acima, que para resolver a equação do primeiro grau solicitada, foram utilizadas algumas operações básicas da matemática a fim de isolar a incógnita x. Ora, se as equações do 1º grau podem ser resolvidas assim, que tal utilizar o mesmo método para resolver as equações do 2º grau completas? Experimentem isolar a incógnita x das equações abaixo e tirem suas conclusões!

2x² + 3x – 5 = 0

x² – x – 6 = 0

x² – 8x + 16 = 0

– x² + 2x – 2 = 0

E aí, deu certo? Quando as equações do 2º grau estão em seu formato completo, não é possível isolar a incógnita x utilizando somente as operações básicas da matemática. Por isso, utilizamos a fórmula de Bhaskara ou o método da soma e produto. Contudo, quando as equações do 2º grau são incompletas, é possível isolar a incógnita x facilmente.

 

3. COMO RESOLVER AS EQUAÇÕES DO 2º GRAU INCOMPLETAS

Como foi dito no início do texto, existem 3 tipos de equações do 2º grau incompletas, e as raízes de cada uma delas possuem um comportamento definido. Nós vamos estudar todos esses comportamentos nos próximos itens. Independentemente do tipo de equação apresentado, a essência das resoluções será sempre isolar a incógnita x. Vem comigo!

 

3.1 Quando os coeficientes b e c são iguais a zero

Quando os coeficientes b e c de uma equação do 2º grau são iguais a zero, o coeficiente a pode assumir qualquer valor real diferente de zero. Independentemente deste valor, as duas raízes da equação devem ser reais e iguais a zero. É o que acontece na equação 5x² = 0, olhem só!

5x² = 0

x² = 0/5

x = ± √0

x = 0

Em casos como esse, a solução da equação pode ser representada por um conjunto unitário.

S = {0}

 

3.2 Quando o coeficiente b é igual a zero

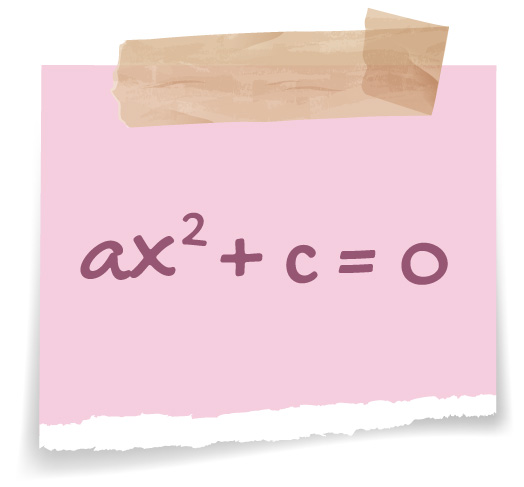
Quando apenas o coeficiente b de uma equação do 2º grau é igual a zero, as suas duas raízes são reais, distintas e simétricas. Isso significa que são dois valores iguais em módulo, mas de sinais opostos. Acompanhem a resolução da equação 3x² – 9 = 0.

3x² – 9 = 0

3x² = 9

x² = 9/3

x = ± √3

S = {–√3, √3}

As raízes da equação 3x² – 9 = 0 são iguais em módulo, √3, mas possuem sinais opostos, ou seja, uma delas é negativa e a outra é positiva. De maneira idêntica, vamos resolver a equação x² – 4 = 0 para verificar se o comportamento se repete.

x² – 4 = 0

x² = 4

x = ±√4

x = ±2

S = {–2, 2}

Perfeito! As raízes da equação x² – 4 = 0 são reais, diferentes e simétricas, ou seja, são iguais em módulo, 2, mas possuem sinais opostos. Tendo isso em vista, até poderíamos seguir para o próximo tipo de equação do segundo grau incompleta. Contudo, um caso especial tal como o da equação x² + 25 = 0 necessita da nossa atenção. Fiquem de olho na resolução desta equação.

x² + 25 = 0

x² = – 25

x = ±√(– 25)

E aí, pessoal, existe ou não existe raiz quadrada de número negativo? No conjunto dos números reais, certamente não! Portanto, algumas equações do 2º grau incompletas de formato “ax² + c = 0” não possuem raízes reais. Nestes casos, a solução da equação pode ser expressa por um conjunto vazio.

S = { }

Tranquilo, não é mesmo? Agora estamos liberados para seguir rumo ao próximo item. Vamos lá!

 

3.3 Quando o coeficiente c é igual a zero

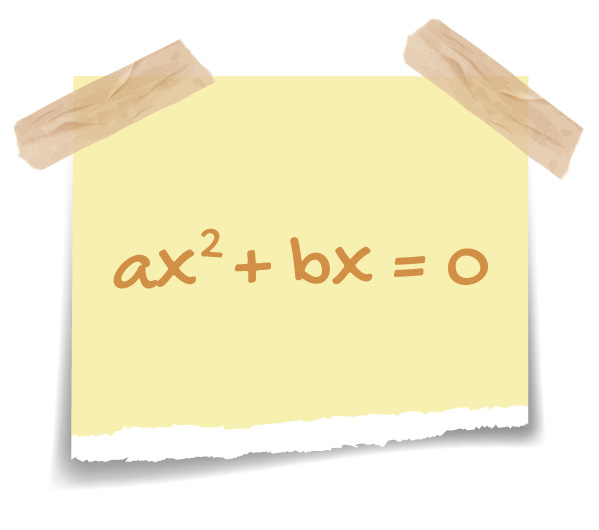
Quando apenas o coeficiente c de uma equação do 2º grau é igual a zero, as suas duas raízes são reais e distintas. Uma delas é sempre igual a zero, e a outra, pode ser qualquer número real diferente de zero.

Para resolver as equações do 2º grau incompletas do tipo ax² + bx = 0, é preciso utilizar um artifício diferente do que foi utilizado nos casos anteriores. Em princípio, devemos realizar a fatoração por fator comum em evidência da expressão “ax² + bx”. Como o produto gerado a partir desta fatoração deve ser igual a zero, em seguida, vamos dar sequência ao cálculo tendo em mente que para um produto ser igual a zero, basta que um de seus fatores seja igual a zero.

x ∙ y = 0

0 ∙ y = 0

x ∙ 0 = 0

Observem o produto entre os fatores x e y logo acima. Para que o resultado obtido a partir desse produto seja igual a zero, basta que x ou que y sejam iguais a zero.

Ficou claro, pessoal? Antes que qualquer dúvida surja, vamos encontrar as raízes de algumas equações do 2º grau do tipo ax² + bx = 0 aplicando esta técnica. Sigam comigo!

 

x² + 5x = 0

x² + 5x = 0

x ∙ (x + 5) = 0

x = 0

x + 5 = 0

x = – 5

S = {– 5, 0}

Reparem que logo no início da resolução, o fator comum, x, entre os dois termos da equação, x² e 5x, foi colocado em evidência. Assim, formou-se o produto entre os fatores “x” e “x + 5”. Para que o resultado deste produto fosse igual a zero, ou “x” ou “x + 5” deveriam ser iguais a zero. Igualando os dois fatores a zero, obtemos, imediatamente, uma das raízes da equação, x = 0. Em seguida, manipulando a equação x + 5 = 0, chegamos a segunda raiz, x = – 5.

 

2x² – x = 0

2x² – x = 0

x ∙ (2x – 1) = 0

x = 0

2x – 1 = 0

2x = 1

x = 1/2

S = {0, ½}

 

4x² – 6x = 0

4x² – 6x = 0

2x ∙ (2x – 3) = 0

2x = 0

x = 0

2x – 3 = 0

2x = 3

x = 3/2

S = {0, 3/2}

Ficou mais claro, pessoal? Tenho certeza de que assim que vocês resolverem uma série de equações do 2º grau incompletas, esses processos ficarão extremamente simples!

Enfim, é chegada a hora de encerrarmos o texto! Espero que o assunto de hoje tenha sido proveitoso, e que a partir deste momento, vocês saibam escolher o método mais adequado para resolver cada tipo de equação do segundo grau!

Gostou desse conteúdo? Clique aqui para saber como a plataforma do Professor Ferretto funciona!

Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!

Caso vocês desejem praticar tudo aquilo que aprenderam até agora, nada melhor do que dar uma olhada no vídeo que está em anexo aqui embaixo. Lá vocês encontram o conteúdo completo sobre as equações do 2º grau! Além disso, quem acompanhar o vídeo vai conferir alguns exercícios resolvidos sobre o assunto, inclusive aqueles que envolvem interpretação. Espero todos lá!

Um abração e até mais!