
Os assuntos de biologia que mais caem no Enem são uma das preocupações de quem está se preparando para a...
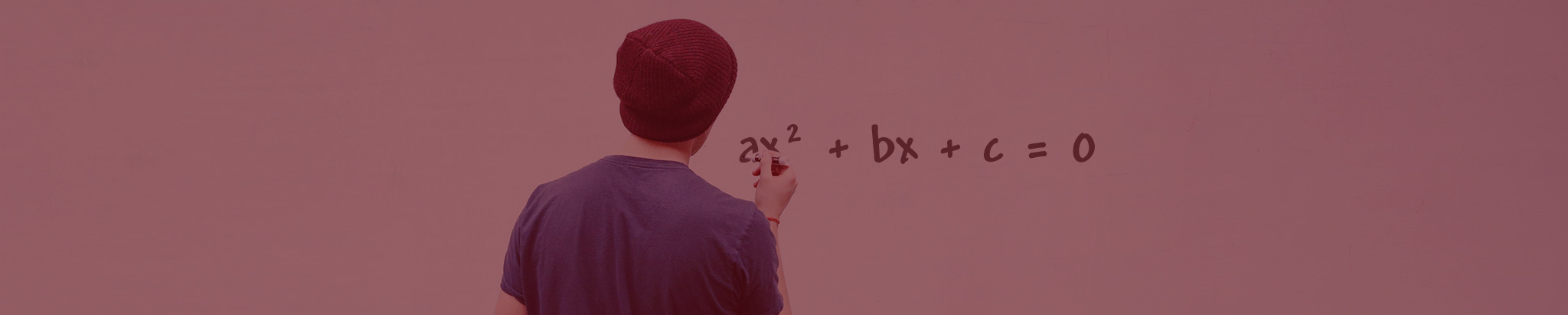
A equação do 2º grau é uma equação que possui o formato ax² + bx + c = 0, com a ≠ 0. Saiba como encontrar as raízes desta equação e resolva exercícios aqui!
O post aborda a definição e a importância das equações do 2º grau no contexto do ensino médio e vestibulares, como o ENEM. Caracteriza a equação do 2º grau e seus coeficientes, fundamentais para identificar e resolver tais equações. Através da explicação de métodos como a fórmula de Bhaskara e o método da soma e produto, o post oferece recursos para resolver equações completas e incompletas. Além de apresentar teoria, o artigo inclui exercícios práticos de vestibular resolvidos, mostrando como aplicar os conceitos aprendidos de maneira eficaz. Finalmente, o texto também reforça a importância do entendimento desses conceitos para o sucesso em provas, oferecendo links para aprofundamento em tópicos específicos relacionados à equação do 2º grau.
A equação do 2º grau é uma equação que possui o formato ax2 + bx + c = 0, com a, b, c ∈ ℝ e a ≠ 0. Quando uma equação do segundo grau se encontra em seu formato completo, é possível resolvê-la utilizando a famosa fórmula de Bhaskara ou então, o método da soma e produto.
Olá, pessoal! Tudo bem com vocês?
Hoje nós vamos tirar um tempinho para abordar um assunto de extrema importância para quem é estudante do ensino médio, e/ou deseja realizar as provas do ENEM e dos vestibulares: a equação do 2º grau. Descobriremos aqui o que é uma equação do segundo grau, estudaremos os seus coeficientes e claro, alguns métodos que nos permitem resolver essas equações. Por fim, resolveremos juntos algumas questões que já caíram em vestibulares e podem ajudar vocês a se prepararem para as provas que irão fazer.
Feito, pessoal? Então, vamos começar! Peguem seus materiais de estudo e sigam comigo!
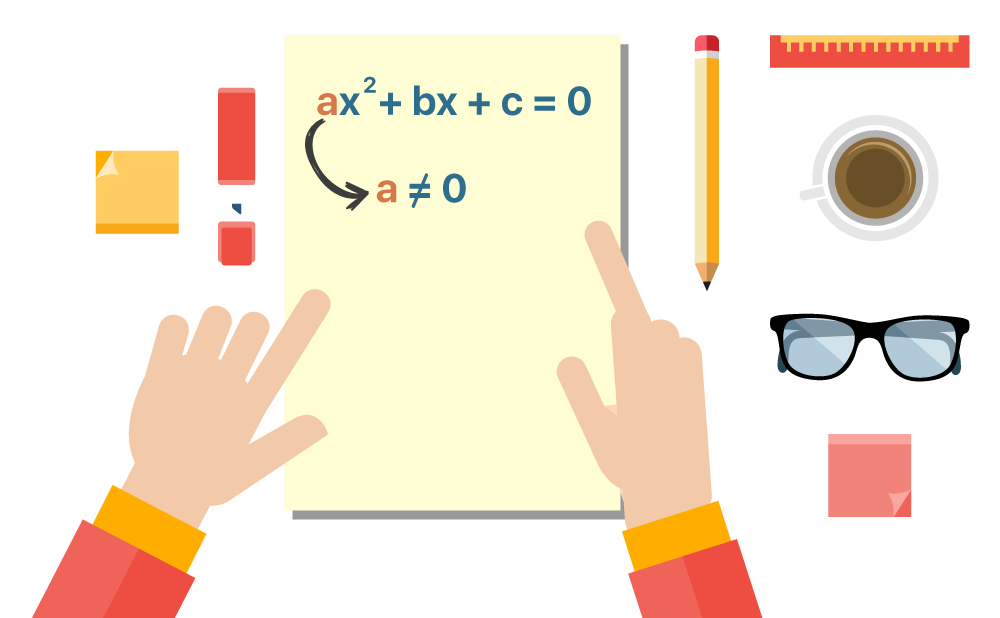
A equação do 2º grau é uma equação que possui o formato ax2 + bx + c = 0, com a, b, c ∈ ℝ e a ≠ 0. Esta equação é definida como do “2º grau” porque é formada por um polinômio de grau 2. Podemos comprovar essa informação observando o formato da expressão com mais atenção. Vejam, o maior expoente da incógnita x é o 2!
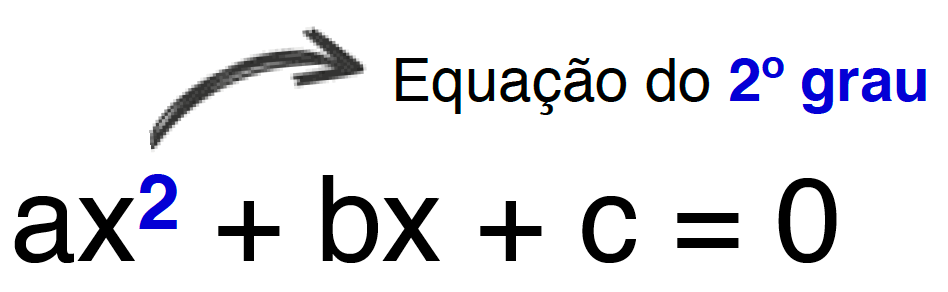
Sabiam que a função quadrática, também conhecida como função do segundo grau, possui um formato muito parecido com o da equação do 2º grau? Quem quiser saber tudo sobre a função quadrática, pode clicar aqui!
![]()
Os coeficientes de uma equação do segundo grau, a, b, e c, são números que pertencem ao conjunto dos números reais (ℝ). Ao contrário de a e b, c não é acompanhado pela incógnita x. Logo, ele é chamado de termo independente da equação do segundo grau. Enquanto isso, b é o coeficiente que acompanha x e por essa razão, é conhecido como coeficiente linear.
Já o coeficiente a, o intitulado coeficiente quadrático, é o valor numérico que acompanha o termo x2. Por causa disso, ele é o coeficiente mais importante da equação do 2º grau. Se o coeficiente a é igual a zero, o termo ax2 deixa de existir, restando apenas a expressão “bx + c = 0”. Uma expressão como essa não representa uma equação do 2º grau, mas sim uma equação do 1º grau, já que aí, o maior expoente de x é de valor 1.
Entendido, pessoal? Vamos destacar os coeficientes de algumas equações do 2º grau para solidificar essa ideia. Acompanhem comigo!

x2 – 5x + 2 = 0
a = 1; b = – 5; c = 2
4x – x2 = 0
a = – 1; b = 4; c = 0
3x2 – 9 = 0
a = 3; b = 0; c = – 9
Reparem nas equações do 2º grau dispostas acima, que o coeficiente a pode ser um valor positivo, negativo, mas jamais pode ser zero, pelas razões que já conhecemos. Contudo, não há restrição alguma em relação aos valores dos coeficientes b e c. Tanto b, quanto c, ou mesmo os dois coeficientes podem ser iguais a zero.
É exatamente esse detalhe que define quando uma equação do 2º grau é completa ou incompleta. Quando a, b e c são valores diferentes de zero, temos uma equação do 2º grau completa. Quando a é diferente de zero, mas b, ou c ou ambos os coeficientes são iguais a zero, temos uma equação do 2º grau incompleta.
Saber diferenciar uma equação do 2º grau completa de uma incompleta pode ser determinante na hora de resolver esse tipo de equação. No próximo item, nós vamos aprender a resolver as equações do segundo grau. Vem comigo!
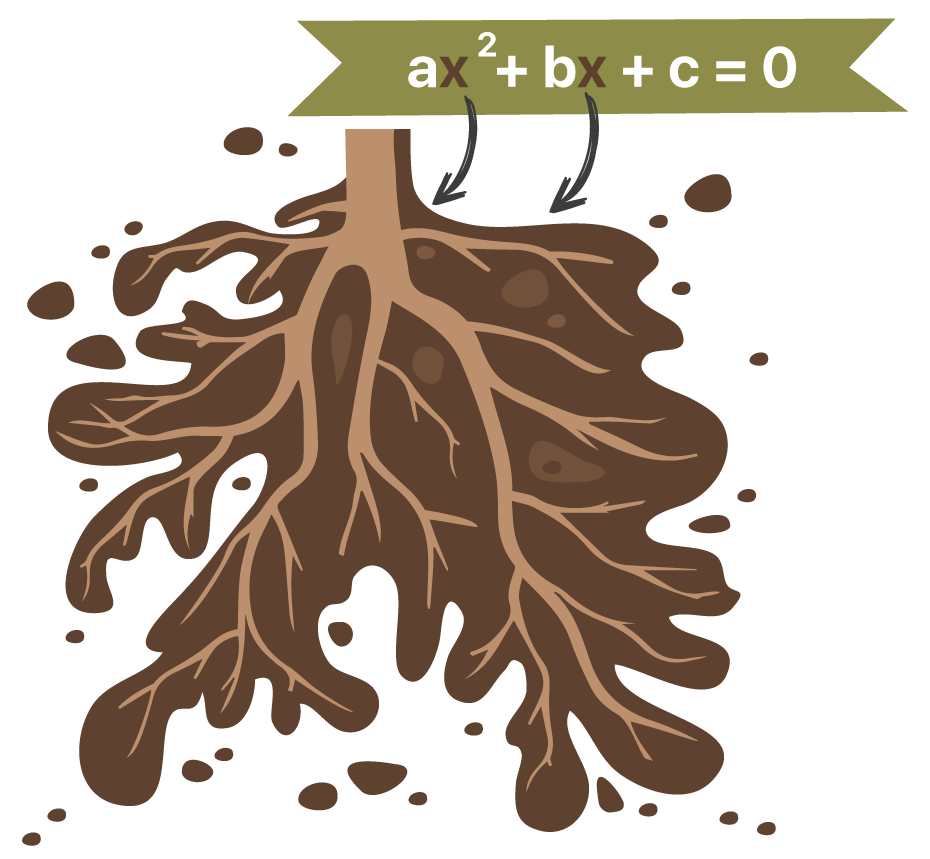
Resolver uma equação do 2º grau “ax2 + bx + c = 0”, significa encontrar os valores de x que tornam o valor da expressão “ax2 + bx + c” igual a zero. Esses valores de x que devem ser encontrados, são conhecidos como as raízes da equação do 2º grau. Falamos em valores ou raízes, sempre no plural, porque por ser formada por um polinômio de grau 2, toda equação do 2º grau sempre possui duas raízes, ou dois valores de x que fazem com que a expressão resulte no valor zero. Geralmente, as raízes da equação do 2º grau são representadas por x1 e x2 ou x’ e x”.
Dois métodos costumam ser utilizados para determinar as raízes das equações do 2º grau. Um deles, é a uma das fórmulas matemáticas mais conhecidas no planeta: a fórmula de Bhaskara. Não menos importante, o método da soma e produto pode nos ajudar a resolver uma equação do 2º grau de forma ainda mais rápida. Nós próximos itens, nós vamos estudar com mais detalhes cada um dos métodos. Sigam comigo!
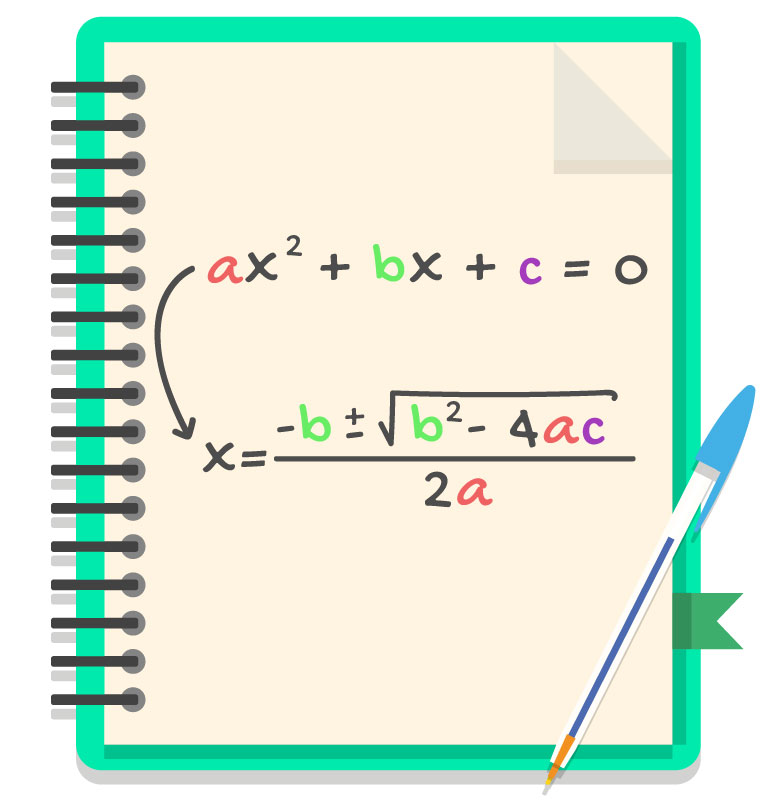
Para encontrar as raízes de uma equação do segundo grau através da fórmula de Bhaskara, basta substituir os valores numéricos dos coeficientes a, b e c da equação na fórmula. Após realizar as operações básicas propostas pela fórmula, chega-se facilmente aos valores de x1 e x2 ou x’ e x” desejados.
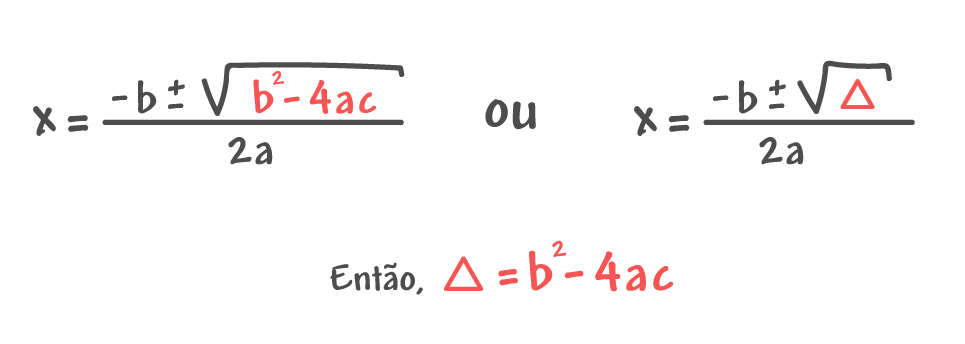
Alguns autores preferem apresentar a fórmula de Bhaskara com base no delta (∆) ou discriminante da função quadrática. Isso porque ao calcular o discriminante, podemos definir o comportamento das raízes da equação do 2º grau, ou seja, se essas raízes são reais e distintas, reais e iguais ou mesmo se elas são complexas. Para saber mais sobre as raízes da função quadrática e o cálculo do discriminante, cliquem aqui!
No último item deste texto, nós vamos resolver alguns exercícios de vestibular e aplicar a fórmula de Bhaskara, fiquem tranquilos! Mas, quem deseja saber mais sobre a história da fórmula de Bhaskara ou conhecer a sua dedução, pode clicar aqui.

O método da soma e produto é considerado bastante prático quando se deseja obter as raízes de uma equação do 2º grau e estas são números inteiros. Nesse método, é preciso pensar em dois números x1 e x2 que quando somados, geram como resultado o valor oposto ou contrário ao quociente entre os coeficientes b e a da equação. Ao mesmo tempo, quando esses dois números x1 e x2 são multiplicados, devem gerar como resultado o valor igual ao quociente entre os coeficientes c e a da equação. Os números x1 e x2 de quem tanto falamos, é claro, são as raízes da equação do 2º grau.
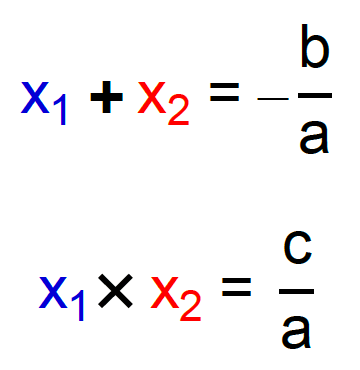
Assim, para utilizar o método com facilidade, a dica é começar pensando nas possibilidades que levam ao produto entre as duas raízes da equação. Depois de elencadas essas possibilidades, basta substituí-las na fórmula da soma, e ver se os resultados se encaixam.
Já já chegará o momento em que iremos aplicar esse método na resolução de exercícios de vestibular. Mas se vocês desejam aprofundar ainda mais os conhecimentos sobre o método, ou conferir uma série de exemplos resolvidos, cliquem aqui! Aqui no blog vocês encontram um texto exclusivo que aborda o método da soma e produto.

Podemos utilizar o método da soma e produto e principalmente a fórmula de Bhaskara para resolver qualquer equação do 2º grau. Contudo, quando as equações do segundo grau encontram-se em seu formato incompleto, existe uma forma ainda mais simples de resolvê-las. Isso porque nesse caso é possível isolar a incógnita x da equação, o que não acontece quando a equação está em seu formato completo.
Na imagem acima, vemos 3 tipos de equações do 2º grau incompletas. Na primeira, os valores numéricos de b e c são iguais a zero. Na segunda, apenas o coeficiente b é de valor zero, enquanto na terceira, apenas o coeficiente c vale zero. Isso é um indício de que cada uma dessas equações pode ser resolvida de uma maneira diferente. Estão curiosos para conhecer melhor esses 3 métodos? Então, cliquem aqui!

(Cesgranrio – adaptada) Se as raízes da equação x2 + bx + 27 = 0 são múltiplos positivos de 3, então, quanto vale o coeficiente b?
Não parece, mas o método da soma e produto pode nos ajudar muito a matar essa charada rapidamente. Nós conhecemos os valores numéricos do coeficiente a e do coeficiente c da equação, não é? Eles valem 1 e 27, respectivamente. Montando as equações propostas pelo método da soma e produto e utilizando esses valores, temos:
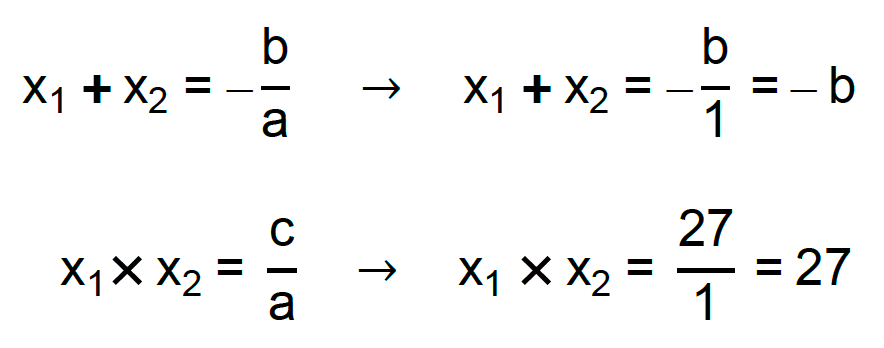
Até então, sabemos que as duas raízes da equação x2 + bx + 27 = 0 são múltiplos positivos de 3, e que o produto entre as mesmas é igual a 27. Aí eu pergunto a vocês: quais são os dois números positivos múltiplos de 3 que quando multiplicados geram como resultado o número 27? A resposta dessa pergunta nos leva ao valor do coeficiente b e consequentemente, a resposta desta questão!
3 x 9 = 27
Assim:
3 + 9 = – b
b = – 12
Incrível, não é mesmo? Vamos ao próximo exercício comigo!
(Uece – adaptada) Se x1 e x2 são raízes da equação 3x2 – 2x – 8 = 0, sendo x1 < x2, então, qual é valor resultante da expressão “3x22 – 2x1 – 8″?
Desta vez, nós vamos encontrar as raízes x1 e x2 da equação 3x2 – 2x – 8 = 0 através da fórmula de Bhaskara. Acompanhem comigo!
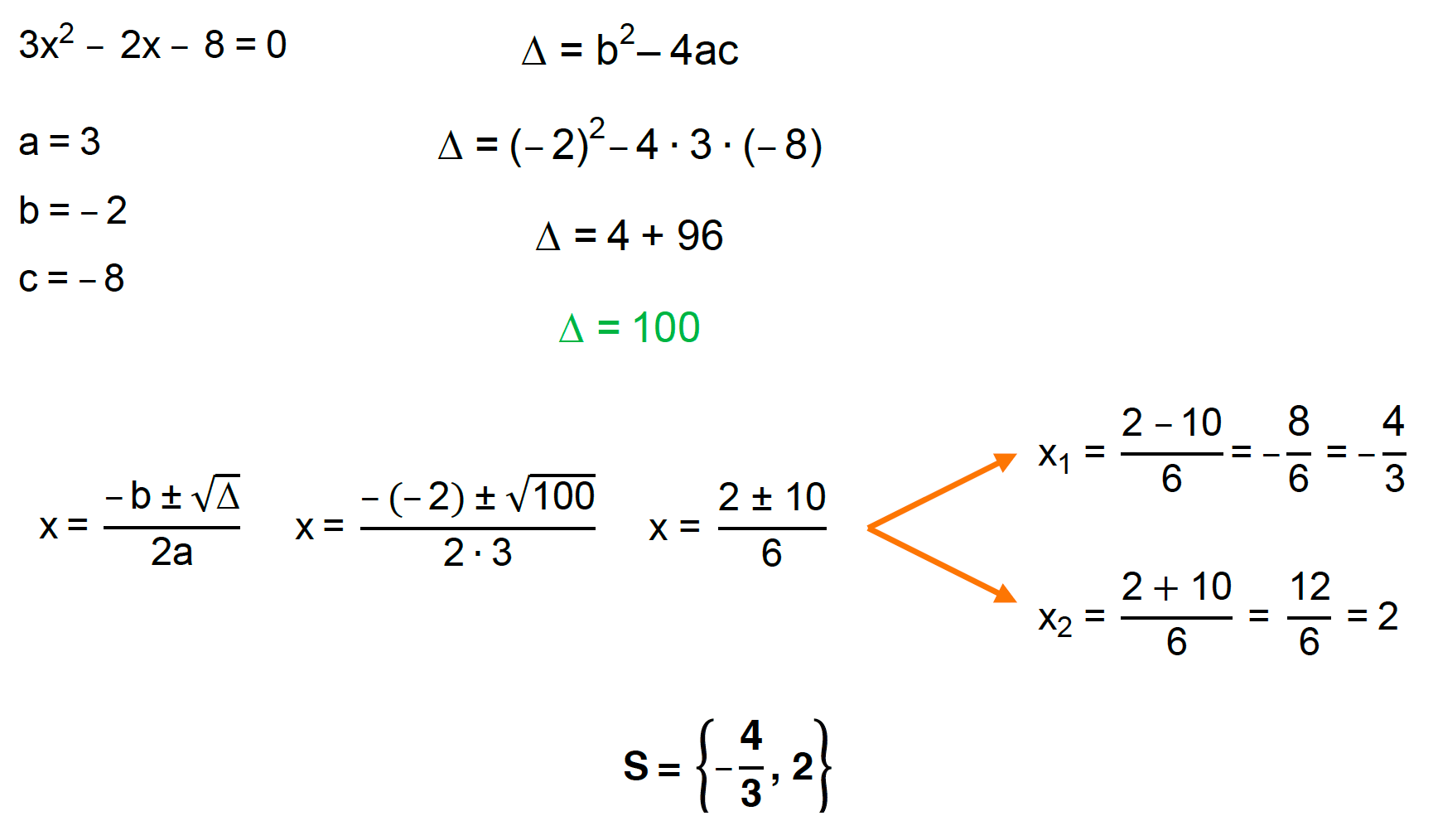
Já que o enunciado afirma que x1 < x2, sabemos que x1 = – 4/3 e x2 = 2. Assim, basta substituirmos esses valores na expressão apresentada para determinarmos o resultado:
3x22 – 2x1 – 8
3∙(2)2 – 2∙(– 4/3) – 8
3∙4 + 8/3 – 8
4 + 8/3
20/3
Tranquilo, não é, pessoal? Então, vamos ao nosso último exercício. Vem comigo!
(Ufv – adaptada) As medidas da hipotenusa e de um dos catetos de um triângulo retângulo são dadas pelas raízes da equação x2 – 9x + 20 = 0. Qual é a área desse triângulo?
Para determinarmos a área do triângulo retângulo descrito no enunciado, precisamos conhecer as raízes da equação x2 – 9x + 20 = 0. Sabemos que os valores numéricos dos coeficientes a, b e c são respectivamente 1, – 9 e 20. Com base nesses valores, vamos utilizar o método da soma e produto para encontrar as raízes. Olhem só!
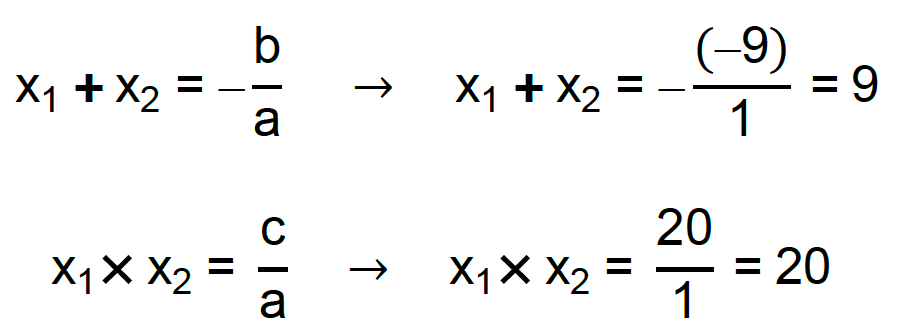
De acordo com a dica que apresentamos neste texto, é melhor começar pelas possibilidades que envolvem o produto entre as duas raízes. Existem alguns produtos entre dois fatores que resultam no valor 20: 1×20, 2×10 e 4×5. Em qual deles encontramos dois valores que somados, resultam em 9?
4 + 5 = 9
4 x 5 = 20
Assim, sabemos que as raízes da equação x2 – 9x + 20 = 0 são x1 = 4 e x2 = 5. Agora, voltamos ao enunciado para seguir com a resolução da questão. Diz-se que as medidas da hipotenusa e de um dos catetos do triângulo retângulo são dadas pelas raízes da equação. Como a hipotenusa é sempre o maior lado de um triângulo retângulo, concluímos que a hipotenusa deste triângulo possui medida igual a 5. Dessa forma, sabendo que um dos catetos do triângulo retângulo mede 4, vamos requisitar o auxílio do teorema de Pitágoras para determinar a medida do outro cateto. Acompanhem!
a2 = b2 + c2
52 = 42 + c2
c2 = 25 – 16
c = √9 = 3
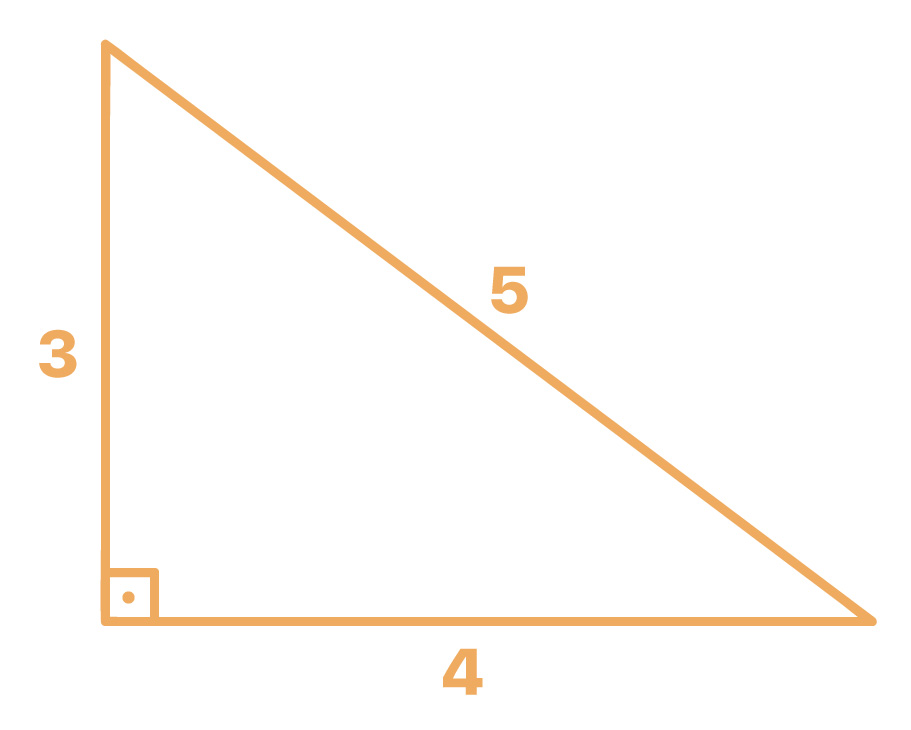
De posse do valor numérico de c, temos condições de calcular a área do triângulo retângulo:
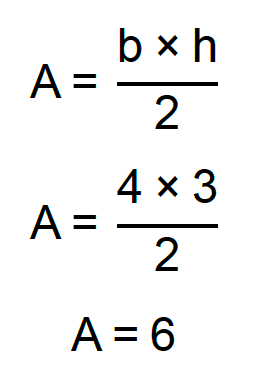
No último exercício resolvido, nós utilizamos conceitos da geometria plana para encontrar a solução requisitada. Cliquem nos links abaixo para tirar todas as dúvidas sobre:
– os elementos do triângulo retângulo (hipotenusa e catetos);
Gostou desse conteúdo? Clique aqui para saber como a Plataforma do Professor Ferretto funciona!
Deseja ter uma preparação completa em matemática e ciências da natureza? Então você precisa conhecer os planos e cursos da plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!
E eu, fico por aqui. Quem quiser acompanhar um apanhado geral sobre a equação do 2º grau e todos os seus métodos de resolução, pode assistir o vídeo que está em anexo logo abaixo. Um abração a todos e bons estudos!
