SISTEMA MÉTRICO DECIMAL

Olá pessoal, tudo bem com vocês?

Hoje vamos ver mais um conteúdo de matemática básica, o Sistema Métrico Decimal. Esse assunto é muito utilizado na prática, em diversas áreas de atuação, por isso, é muito importante que vocês saibam todas as unidades e transformações do nosso sistema de medidas!

E se vocês quiserem um curso completo de matemática básica para o Enem, assinem a plataforma do Professor Ferretto. Lá vocês terão acesso aos conteúdos de matemática básica e matemática do ensino médio preparatórios para o Enem e para o vestibular. Acessem e confiram os benefícios oferecidos pelo curso!

Vamos lá? Então, vem comigo aqui!

 

1. UNIDADE FUNDAMENTAL

O sistema métrico decimal é totalmente embasado em uma unidade fundamental. No Brasil essa unidade fundamental é o metro, que é representado pela letra m minúscula. A partir do metro, existem outras unidades a sua direita, como também outras unidades a sua esquerda. As unidades a esquerda são classificadas como múltiplos do metro. Já as unidades que se encontram a direita são classificadas como submúltiplos do metro. Nós vamos ver quais são os múltiplos e os submúltiplos em relação ao metro na sequência.

 

1.1 Múltiplos e submúltiplos do metro

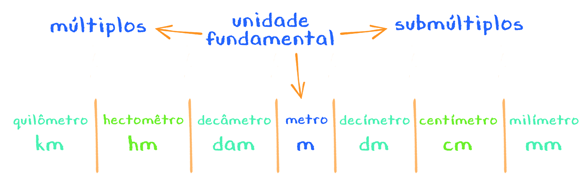
Observem na imagem acima que no lado esquerdo da unidade fundamental estão os múltiplos do metro. Estes múltiplos são divididos em três unidades, são elas: o decâmetro, representado pelo dam, o hectômetro, que é representado pelo hm, e por último, a mais utilizada em relação aos múltiplos, que é o quilômetro, representado por km.

Se vocês olharem novamente a imagem, a direita do metro, encontrarão também três submúltiplos. O primeiro submúltiplo é o decímetro, representado pelo dm, o próximo submúltiplo é o centímetro, representado pelo cm, e a última unidade de submúltiplos em relação ao metro é o milímetro, representado por mm.

Agora, vamos ver quanto vale cada múltiplo e submúltiplo em relação ao metro. Se definirmos 1 metro, por exemplo, em relação a esse metro o decâmetro vale 10 vezes mais, ou seja, o decâmetro equivale a 10 m. O hectômetro vale 100 vezes mais ou seja, equivale a 100 m, da mesma forma que o quilômetro vale 1000 vezes mais, sendo igual a 1000m. Perceberam o que vai acontecendo? Para os submúltiplos ocorre a mesma coisa, só que ao contrário, olhem só: o decímetro em relação ao metro vale 10 vezes menos e equivale a 0,1m; já o centímetro vale 100 vezes menos e equivale a 0,01 m da mesma forma que o milímetro equivale a 0,001m, ou seja vale 1000 vezes menos. Vejam o esqueminha abaixo para entender tudo isso melhor:

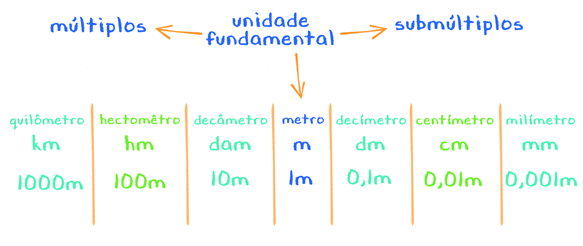
É muito importante que vocês memorizem esse quadro métrico expresso acima. Tentem criar uma frase que lembre cada um dos termos da tabela! Enquanto isso, vamos falar um pouco sobre a leitura de uma distância no sistema métrico decimal.

 

1.2 Leitura

Para entendermos como deve ser feita a leitura de um número, vamos usar alguns exemplos, que são a melhor maneira de explicar esse item.

Vamos começar com o exemplo de 13,024 m. Ao nos depararmos com números assim, normalmente lemos 13,024 metros, o que não está errado. Mas existe uma maneira mais específica de realizar a leitura de termos como esse em relação ao sistema métrico decimal. É isso que iremos aprender agora!

Para isso, vamos montar o quadro de unidades e analisar o número 13,024. Observem que esse número é formado por duas partes, uma parte inteira composta por 2 algarismos (13) e outra parte decimal composta por 3 algarismos (024).

Primeiramente, vamos pegar o último algarismo da parte inteira e colocar ele exatamente na coluna em que se encontra o metro, e junto dele colocamos a vírgula. Agora, vamos completar com os outros números. Temos o 1 a esquerda do 3, então, ele irá na coluna do decâmetro e a parte decimal, composta de 3 algarismos, ocupará as 3 colunas a direita do metro no quadro de unidades.

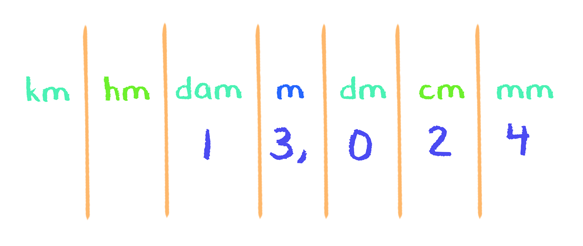
Feito isso, vamos ver como é a leitura desse número. Nós vamos ler a parte inteira e a parte decimal separadamente, sempre colocando a unidade relativa ao último algarismo de cada parte. Querem ver como fica? Olhem só, em relação a parte inteira composta pelos dois algarismos, nós lemos o 13 e a unidade será o metro, pois o último algarismo, o 3, está na coluna do metro.

Já em relação a parte decimal, composta de 3 algarismos, nós não iremos ler 024, vamos ler 24. O último algarismo, o 4, está na coluna dos milímetros, logo:

Treze metros e vinte e quatro milímetros.

Vamos fazer mais um exemplo, agora 8,03 km. Vamos ver como seria a leitura desse número em relação ao quadro de unidades. Colocamos a parte inteira, que é o 8, na coluna dos quilômetros, e a vírgula junto ao 8. Já os dois algarismos da parte decimal, o 0 e 3, nós colocamos um em cada coluna a direita do 8.

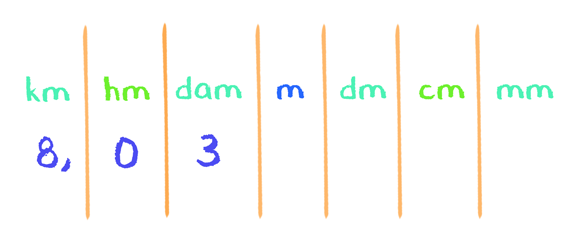
Agora, nós lemos a parte inteira junto da unidade de quilômetro e a parte decimal, junto a unidade do último algarismo, ou seja, do decâmetro. Então ficamos com:

Oito quilômetros e três decâmetros.

Entenderam a ideia? Agora, vamos ver a principal parte deste conteúdo, que é a transformação de unidades de números que se encontram no sistema métrico decimal.

 

2. TRANSFORMAÇÃO DE UNIDADES

2.1 Unidade de comprimento

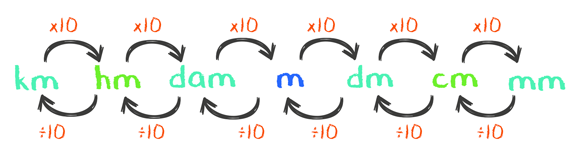
Na transformação de unidades, quando queremos transformar um número, por exemplo, que está na unidade de quilômetros e reescrevê-lo na de unidade hectômetro, o que precisamos fazer é uma multiplicação por 10. Mas, se quisermos transformar de quilômetro para decâmetro, são dois saltos para a direita, logo, teremos uma nova multiplicação por 10, bem como mostra a figura acima, viram lá? Assim, vocês fazem uma multiplicação por 10 e depois outra multiplicação por 10, ou seja, uma multiplicação por 100.

É sempre a mesma ideia, passando de uma unidade que se encontra mais a esquerda para uma que se encontra mais a direita, a cada salto haverá uma multiplicação por 10.

Agora, para fazermos o processo contrário, ou seja, passarmos um número que esteja na unidade milímetro para centímetro, de centímetro para decímetro e assim por diante, a gente faz a divisão e não a multiplicação. Antes a gente multiplicava por 10, agora vamos dividir por 10 a cada salto.

Ok? Vamos fazer um exemplo para ficar mais fácil o entendimento. Se tivermos um número na unidade de hectômetro e desejamos transformá-lo para metros.

Para fazermos essa transformação, vamos lembrar do quadro lá em cima: do hectômetro para o metro, são dois saltos para a direita, e a cada salto há uma multiplicação por 10. Então, do hectômetro para metro temos uma multiplicação de 10 vezes 10, ou seja, vezes 100.

Tranquilo né, pessoal!? Fizemos apenas transformações usando unidades de comprimento, mas também podemos utilizar transformações em áreas e volumes, utilizando quase o mesmo quadro. Vamos ver cada uma delas a seguir.

 

2.2 Unidades de área

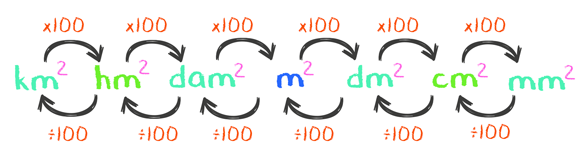
Vocês deram uma olhada na figura acima? Qual é a diferença do quadro apresentado acima em relação ao anterior? Lembrem que no cálculo de áreas, as unidades estão sempre ao quadrado, pois tratam-se de duas dimensões, comprimento e largura.

Então, para transformar uma unidade que está em quilômetro quadrado, para uma que está em hectômetro quadrado, haverá um salto para a direita, mas precisamos considerar o expoente na multiplicação. Deixa eu explicar melhor: quando era comprimento a gente multiplicava por 10, mas agora que as unidades estão elevadas ao quadrado, será 10², ou seja, a multiplicação será por 100.

Se a gente quiser transformar de quilômetro quadrado para decâmetro quadrado, haverá dois saltos para a direita, ou seja, haverá duas vezes a multiplicação por 100. Dessa forma faremos a multiplicação por 100², que será de 10 000. E assim funciona para todos os saltos de unidades que estão mais à esquerda, para as que estão mais a direita.

Quando queremos fazer o contrário, ou seja, transformar de milímetro quadrado para centímetro quadrado, há uma divisão por 100. A cada salto dividimos por 10² para transformar para a unidade que queremos.

Vamos fazer um exemplo, para vocês aprenderem direitinho:

Se olharmos para o quadro de unidades, de km² para m² são 3 saltos, ou seja, será 100 vezes 100 vezes 100.

 

2.3 Unidades de volume

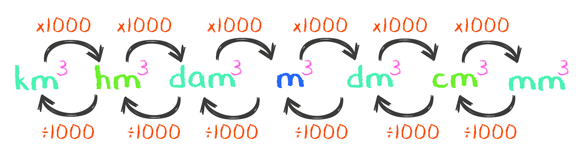
As unidades de volume seguem a mesma regra em relação a área. Na área, as unidades estão ao quadrado, enquanto no volume as unidades estão colocadas ao cubo, pois temos três dimensões, comprimento, largura e altura. Imagino que vocês repararam nisso no quadro acima.

Vamos transformar então, por exemplo, um número que esteja em quilômetros cúbicos para hectômetros cúbicos. Novamente o expoente deve ser considerado. No comprimento, nós multiplicávamos por 10, na área por 100, e agora faremos a multiplicação por 1000, ou seja, 10³. Assim vale para os demais números, ou seja, a cada salto para a direita temos uma multiplicação por 1000.

E quando queremos fazer o processo inverso, ou seja, de unidades mais a direita para unidades mais a esquerda, devemos fazer, como vocês já imaginam, a divisão por 1000.

Vamos fazer um exemplo para que fique mais claro para vocês. Vamos transformar:

Vamos localizar no esquema, de m³ para cm³ temos que dar dois saltos para a direita, ou seja, multiplicamos por 1000 e depois por 1000 novamente.

Tudo certo até aqui? Agora vamos ver algumas relações importantes em relação ao litro, a unidade fundamental do volume.

 

3. RELAÇÕES IMPORTANTES

 

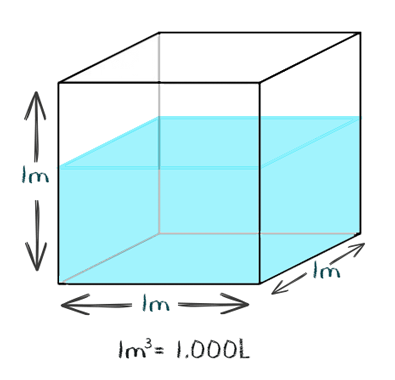
Acabamos de ver, no sistema métrico decimal, as unidades de volume. Mas, é comum aparecer volume expresso pela sua unidade fundamental, o litro. Vamos falar a respeito de algumas relações importantes em relação ao litro, são essas especificadas abaixo:

1. 1 centímetro cúbico é igual a 1 mililitro;
2. 1 decímetro cúbico equivale a 1 litro e;
3. 1 metro cúbico equivale a 1000 litros.

Vejam só o esqueminha abaixo para ficar mais fácil:

 

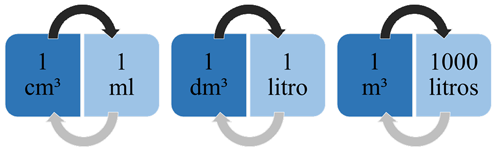
Agora que vocês aprenderam tudinho sobre o sistema métrico decimal e suas transformações de unidades, encerro o texto de hoje deixando em anexo um vídeo sobre o assunto, que tem outros exemplos e exercícios resolvidos, para que vocês aprendam ainda mais sobre o conteúdo. Assim, vocês podem ficar tranquilos para a prova do Enem, e também do vestibular.

Espero que o texto ajude muito vocês nos estudos e nas provas que irão realizar!

Um abração! Até o próximo texto!