JUROS SIMPLES E SUA RELAÇÃO COM FUNÇÃO AFIM E PROGRESSÃO ARITMÉTICA
27/12/2017
Olá pessoal, tudo bem?
Vamos falar agora sobre um assunto específico da matemática financeira, os juros simples. Mesmo os juros simples não sendo os principais juros usados nas operações financeiras, eles são muito utilizados em questões não só do Enem, mas de diversos vestibulares. Para saber mais sobre os conteúdos da matemática financeira, assine a plataforma Professor Ferretto e tenha acesso à videoaulas explicativas, exercícios resolvidos, material didático e tudo o que você precisa pra apender direitinho o conteúdo.
Certinho!? Então vem comigo aqui!
1. DEFINIÇÃO DE JUROS SIMPLES

Vou usar um exemplo que provavelmente vocês já tenham vivenciado em algum momento, ou então algum amigo ou familiar. Quem nunca emprestou dinheiro, né?! Vamos imaginar que um amigo pediu para você exatamente R$ 180,00 emprestados por um mês. Ao final deste período o seu amigo devolveu os R$ 180,00 por ele emprestados e, além disso, pagou R$ 9,00 pelo empréstimo.
Então pessoal, esse pagamento pelo empréstimo é chamado de juro (j), a quantia que você emprestou é chamada de capital inicial (C), a soma do capital inicial com o juro é chamada de montante (M) e a razão entre o juro e o capital inicial é chamada de taxa de juros (i).
Vou explicar de outra forma pra ficar mais fácil o entendimento para vocês. Imagine que você possui uma certa quantia (capital) e aplique ela em uma caderneta de poupança por um determinado período (tempo), como se você estivesse fazendo um empréstimo ao banco. Mesmo os bancos não trabalhando com o sistema de juros simples, vamos imaginar isto apenas como um exemplo para você entender melhor os juros simples. Então, no final deste período, você recebe uma quantia (juros) como compensação. O valor dessa quantia é estabelecido por uma porcentagem (taxa de juros) e ao final da aplicação você terá em sua conta a quantia correspondente ao capital que você investiu mais os juros desta aplicação (montante).
Fácil né?! Desta forma, podemos dizer que se um capital C, aplicado à taxa de i% ao período, no sistema de juros simples, rende juros no fim de t períodos, então:
i . C = juros obtidos no final de 1 período
i . C . t = juros obtidos no final de t períodos
Ou seja, podemos calcular o juro ao final de um determinado período por:
J = C . i . t
É muito importante que vocês lembrem sempre que a taxa e o tempo devem se referir a mesma unidade de tempo (% ao mês e meses, % ao dia e dias, % ao ano e anos, e assim por diante). Quando aparecerem problemas com unidades de tempo diferentes, basta fazer uma regra de três e transformar em apenas uma das unidades.
Para que vocês aprendam melhor, vamos calcular a taxa de juros que o seu amigo pagou ao acrescentar R$ 9,00 ao empréstimo.
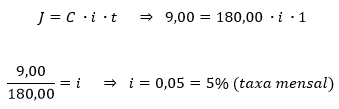
Então, ele pagou uma taxa mensal de 5% sobre o dinheiro que você emprestou para ele. E quanto esse juro rendeu para você no final das contas? Podemos descobrir isso através do montante (M), que nada mais é do que a soma do capital investido com o juro adquirido no final de um determinado período. Logo, o montante é dado por:
M = C + J
Vamos descobrir o montante que você obteve no final deste mês emprestando o dinheiro ao seu amigo:
M = 180,00 + 9,00 M = 189,00
Logo, você recebeu R$ 189,00 após um mês de empréstimo. De forma simples pessoal, o juro é a remuneração que você recebe ao emprestar ou aplicar um capital durante certo tempo.
Agora observem o seguinte, caso o seu amigo tivesse pedido um tempo maior para devolver o dinheiro, a cada mês ele iria pagar um valor de R$ 9,00 a mais sobre o valor emprestado, isto porque a taxa incide sempre sobre o capital inicial.
Como o juro é constante ao longo de um determinado período, o montante acumulado possui relação direta com a função afim e também com as progressões aritméticas. Vou mostrar para vocês como isso acontece e como é dada essa relação. Vamos lá!
2. JUROS SIMPLES E FUNÇÕES
As aplicações no regime de juros simples estão relacionadas às funções, como por exemplo a função linear e a função afim. Vou usar um exemplo pra vocês entenderem melhor essa relação. Vamos supor um capital de R$ 800,00 aplicado à taxa de 40% (0,4) ao ano.
No sistema de juros simples, os juros são obtidos em função do tempo de aplicação, através da equação:
j = 800 . 0,4t j = 320t
Essa função tem uma equação do tipo da função linear f(x) = ax. Ela pode ser representada desta forma:
J = f(t) = 320t
Ainda no sistema de juros simples, o montante é obtido em função do tempo, e a equação dessa função é do tipo função afim, dada por:
M = 320t + 800
Os gráficos representativos das funções acima são representados por uma reta, ou seja, nas operações de juros de simples os juros crescem de forma linear. Desta forma, os gráficos ajudam em análises sobre o andamento do montante formado mês a mês, permitindo que a gente possa comparar diferentes aplicações pra ver qual delas é mais vantajosa dentro de um determinado período.
Vamos fazer o gráfico representativo do montante desta operação financeira citada acima, M= 320t + 800. Para isso, vamos montar uma tabelinha com alguns valores de tempo (t) e calcular o montante (M) correspondente.
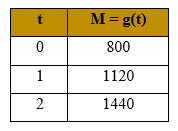
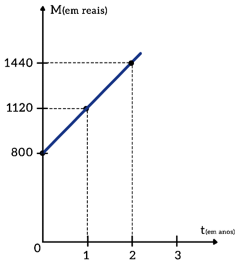
Agora, vou mostrar para vocês como os juros simples podem se relacionar com uma PA.
3. JUROS SIMPLES E PROGRESSÃO ARITMÉTICA

As operações financeiras envolvendo juros simples também podem ser associadas a progressões aritméticas. Vou usar um exemplo para vocês verem como é dada essa relação e como é simples de entender.
Pensem no seguinte caso, Marina aplicará R$ 1000,00 a juros simples de 2% ao mês. Contando o capital aplicado por ela mais o juro a receber, quanto ela terá ao final de um mês? De dois meses? De três meses? De t meses?
Pessoal, lembrem que a aplicação juros simples de 2% ao ano, significa que, a cada mês, Marina receberá de juro a quantia de 2% do capital aplicado.
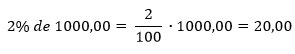
Desta forma, contando o capital aplicado mais o juro recebido ela terá (em reais):
- Após um mês:
1000,00 + 20,00 = 1020,00
- Após dois meses:
1000,00 + 2 ‧ 20,00 = 1040,00
- Após três meses:
1000,00 + 3 ‧ 20,00 = 1060,00
- Após t meses:
(1000,00 + t ‧ 20,00)
O capital aplicado mais o juro somam o que chamamos montante da aplicação. Notem que o capital inicial e os montantes no final de cada mês formam uma PA. Mas qual será a razão dessa PA?
Vamos montar a sequência de cada termo, para descobrir a razão dessa PA:
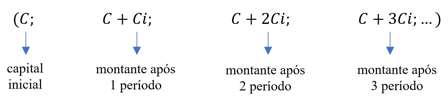
Percebam que a diferença de um termo para o outro é Ci. Assim, a razão dessa PA, Ci, é o juro recebido em um período de aplicação.
Finalizamos mais um texto, e eu acredito que o aprendizado de hoje ajudará muito vocês não só na prova do Enem e dos vestibulares, mas também nas operações financeiras que vocês precisem fazer. Agora que vocês já sabem como os juros simples podem se relacionar com uma função afim e também com uma PA, procurem realizar exercícios de formas diferentes e aprender ainda mais sobre o assunto.