
Quais sĂŁo as propriedades da matĂŠria? Veja exemplos e exercĂcios resolvidos As propriedades da matĂŠria sĂŁo as caracterĂsticas, os comportamentos...
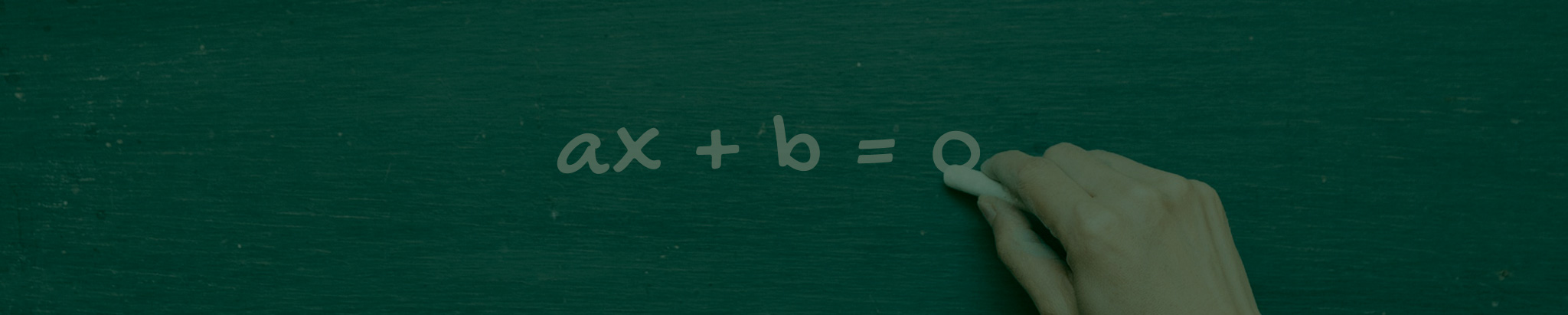
Ao interpretarmos certas situaçþes, podemos cair nas chamadas equaçþes do 1º grau. Você sabe quem são elas e como resolvê-las? Não? Então acompanhe o texto!
Uma equação do primeiro grau ĂŠ uma igualdade que possui o formato ax + b = 0, com a, b â â e a â 0. Resolver uma equação do 1Âş grau significa encontrar sua raiz, ou seja, obter o Ăşnico valor numĂŠrico que torna a igualdade verdadeira.
Â
OlĂĄ, pessoal! Tudo bem com vocĂŞs?
Estamos aqui hoje para falar de um assunto da matemĂĄtica muitĂssimo importante para quem pretende realizar provas de vestibulares, o ENEM, e tambĂŠm alguns concursos pĂşblicos. Vamos conhecer a equação do primeiro grau! Entenderemos sua definição, como ĂŠ possĂvel encontrar sua raiz e, de quebra, tambĂŠm faremos vĂĄrios exercĂcios para consolidar o conhecimento no assunto.
Preparados para começar? Então, sem mais rodeios, vamos lå!
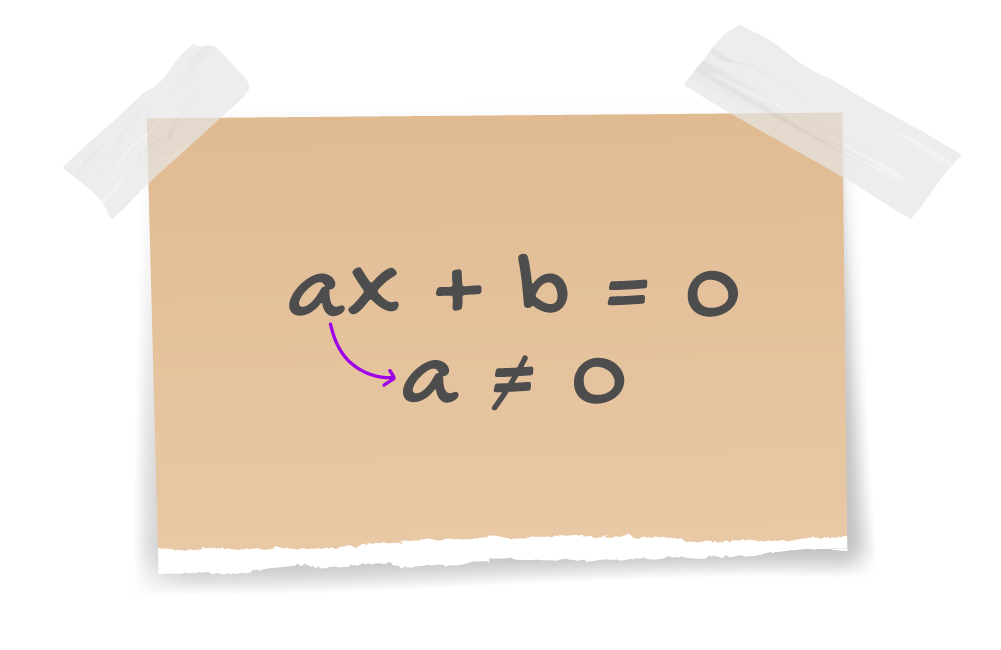
Toda expressão algÊbrica Ê composta por números, operaçþes e por certos valores desconhecidos. Estes valores desconhecidos geralmente são representados por letras, tais como x. Quando expressþes como essas são inseridas em uma igualdade, temos a formação de uma equação.

O grau de uma expressĂŁo algĂŠbrica, e portanto de uma equação, ĂŠ definido pelo maior expoente da incĂłgnita da expressĂŁo. Na equação ax + b = 0, a e b sĂŁo nĂşmeros reais, sendo a diferente de zero, ou seja, eles sĂŁo os valores numĂŠricos conhecidos da equação. O valor desconhecido, ou a incĂłgnita da expressĂŁo, ĂŠ o x! Como este nĂŁo possui um expoente visĂvel, significa que ele vale 1.
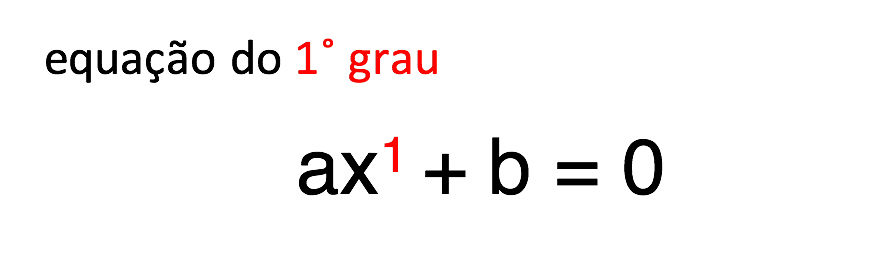
Agora vocĂŞs entenderam por que o valor de a nĂŁo pode ser igual a zero em uma equação do primeiro grau? Pessoal, caso o a fosse zero, irĂamos ter 0 vezes x, ou seja, ficarĂamos com zero, e o termo ax acabaria sumindo. Desta forma, nĂłs nĂŁo terĂamos mais uma equação do 1Âş grau, e sim um valor constante, o b.
Portanto, lembrem sempre! Para que uma equação do 1º grau exista, Ê necessårio que ela esteja na forma ax + b = 0, com o a diferente de 0. Jå quanto ao valor de b não hå restrição alguma. Ele pode ser qualquer número real.
Entendido? Antes de aprendermos como resolver uma equação do primeiro grau, vamos estudar a localização dos coeficientes a e b em algumas equaçþes. Venham comigo!
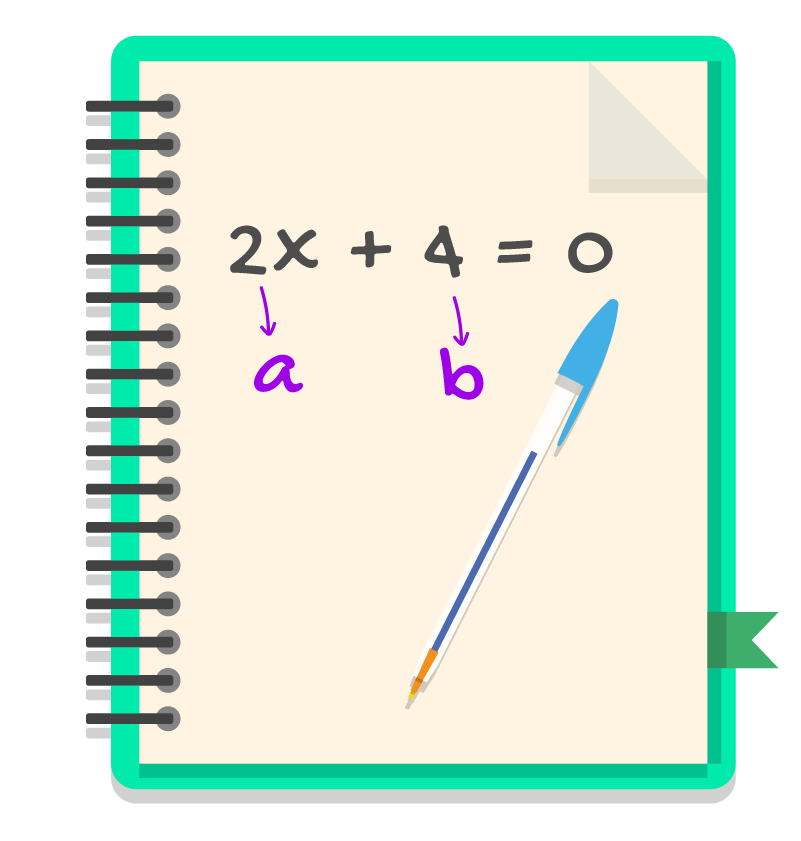
O coeficiente a de uma equação do primeiro grau sempre serĂĄ o valor que estĂĄ multiplicando x, ou a incĂłgnita da equação. JĂĄ o coeficiente b ĂŠ o chamado termo independente da equação do 1Âş grau, ou seja, nĂŁo depende do valor da incĂłgnita, ĂŠ âsozinhoâ.
Bom, para quem estå achando muito simples diferenciar os valores de a e b, eu confirmo, Ê só isso mesmo! Contudo, existe um detalhe importante ao qual vocês devem ficar atentos: o sinal do valor numÊrico! A forma geral da equação do 1º grau não possui sinal negativo. Por isso, se algum sinal como esse aparecer, pertencerå ao seu respectivo coeficiente, olhem só!
3x â 5 = 0    â   a = 3 e b = â 5
7 + žx = 0    â   a = ž e b = 7
â 8x â 2 = 0    â   a = â 8 e b = â 2
6x = 0   â   a = 6 e b = 0
Beleza, pessoal? Agora estamos preparados para aprender a resolver as equaçþes do primeiro grau. Vamos comigo ao próximo item!
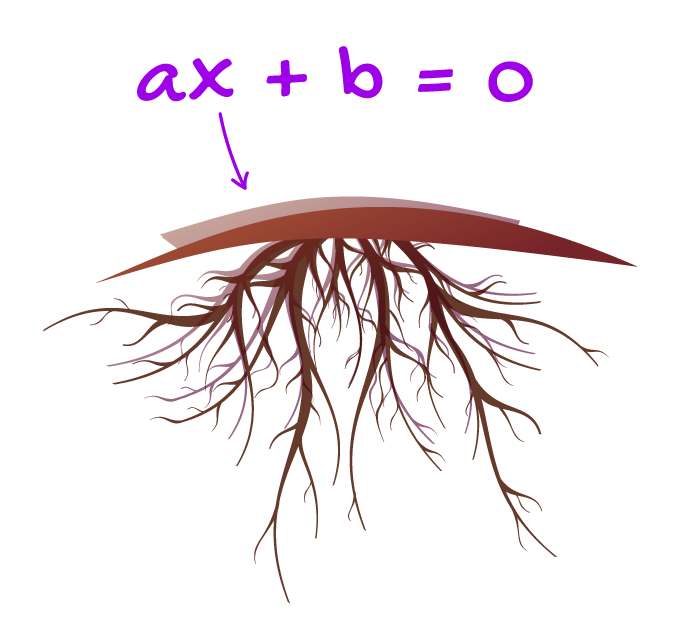
Resolver uma equação nada mais Ê do que encontrar sua raiz, ou o valor que torna a igualdade verdadeira. E quando se trata de uma equação do primeiro grau, esse processo Ê extremamente simples.
O primeiro passo consiste em associar os termos semelhantes. Em outras palavras, deve-se unir todos os termos que acompanham a incĂłgnita x e todos os termos que nĂŁo a acompanham. AĂ ĂŠ sĂł deixar os termos dependentes de x a esquerda da igualdade e os termos independentes de x a direita da igualdade.
No mais, basta realizar as 4 operaçþes båsicas, tais como adição, subtração, multiplicação ou divisão. Só não då para esquecer de trocar o sinal dos termos quando estes estão somando ou subtraindo e mudam de lado da igualdade, ok? Vamos resolver alguns exemplos para que fique mais claro.
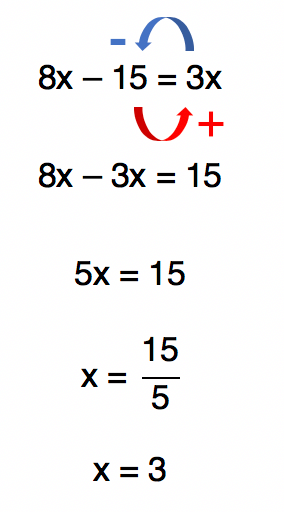
Assim, nós podemos dizer que a raiz da equação que acabamos de resolver Ê 3. Muitas vezes, a solução de uma equação do 1º grau Ê dada em forma de conjunto solução, conforme vemos abaixo:
S = {3}
E aĂ, perceberam que a equação 8x â 3x = 15 nĂŁo estava exatamente no formato ax + b = 0? Bom, se o objetivo de vocĂŞs for encontrar a raiz de uma equação do 1Âş grau, o formato em que ela aparece nĂŁo irĂĄ interferir, acreditem. De outra forma, jamais poderĂamos resolver o prĂłximo exemplo, olhem sĂł!
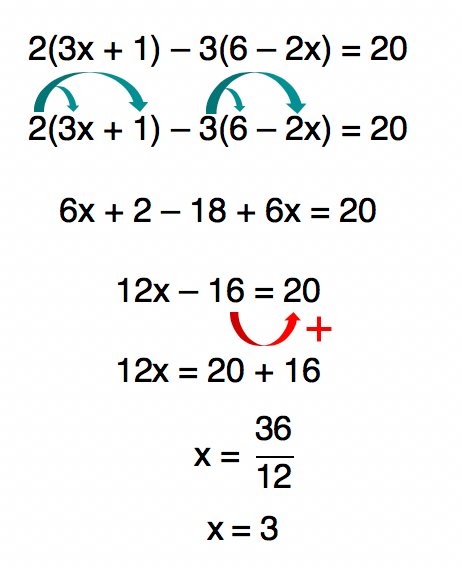
Portanto:Â S = {3}
Neste Ăşltimo exemplo, foi necessĂĄrio utilizar a propriedade distributiva no inĂcio da resolução. No prĂłximo item, vamos conhecer uma variação da equação do 1Âş grau. Para resolvĂŞ-la, um outro artifĂcio matemĂĄtico serĂĄ muito utilizado. Sigam comigo!

Uma equação fracionåria Ê formada por uma sÊrie de fraçþes, em que pelo menos uma delas conta com uma incógnita no denominador. Se a incógnita da equação fracionåria tiver como expoente o número 1, podemos resolvê-la como resolvemos uma equação do primeiro grau, apenas prestando atenção em mais um detalhe bem importante.
Se estamos falando de fraçþes, sabemos que vamos nos deparar com numeradores e denominadores. O numerador de uma fração pode ser qualquer número real. Contudo, o denominador de toda e qualquer fração jamais pode ser zero. Por esse motivo, precisamos prestar muita atenção na solução encontrada para uma equação fracionåria.
Entendido? Tendo tudo isso em vista, vamos descobrir com um exemplo como encontrar a raiz de uma equação fracionåria. Acompanhem!
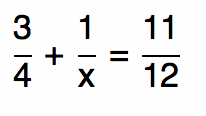
O primeiro passo para resolver uma equação fracionĂĄria em que os denominadores sĂŁo diferentes ĂŠ encontrar um denominador comum, como ĂŠ feito em qualquer soma ou subtração de fraçþes usual. Por isso, vamos calcular agora o MMC ou o MĂnimo MĂşltiplo Comum entre os denominadores 4, x e 12 da equação exemplo. Se vocĂŞs nĂŁo conhecem o MMC, ou desejam saber tudo sobre essa operação, deem um pulo no texto MĂnimo MĂşltiplo Comum e suas Propriedades.
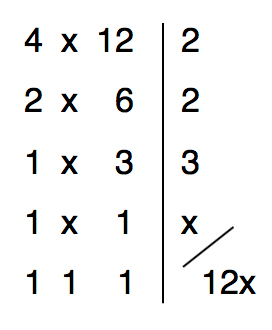
Conhecendo o MMC, vamos continuar a operação:
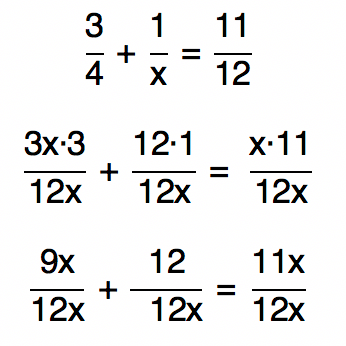
Repararam que neste momento os denominadores sĂŁo todos iguais? Podemos entĂŁo, sem problema algum, continuar trabalhando apenas com os numeradores:
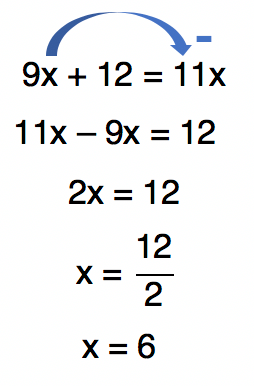
6 ĂŠ diferente de zero, certo? Portanto S = {6}.
Entendido, pessoal? AtÊ aqui sempre resolvemos equaçþes que nos eram dadas diretamente. Mas sabemos que na maioria das provas, sejam elas do ENEM ou dos vestibulares, nós precisamos interpretar certas situaçþes que resultam em uma equação do primeiro grau. Infelizmente, Ê aà que mora o problema, não Ê mesmo?! Se vocês querem aprender a resolver casos como esse, venham comigo atÊ o próximo item!

No final do mês de outubro, os estudantes Carlos e Artur haviam gastado, respectivamente, dois terços e três quintos de suas mesadas. Embora a mesada de Carlos seja menor, ele gastou R$ 8,00 a mais do que Artur. Se a soma dos valores das duas mesadas Ê R$ 810,00, qual Ê o valor monetårio da diferença entre os valores das duas mesadas?

Analisando as informaçþes que foram dadas, ĂŠ possĂvel dizer que a mesada de Carlos (C) somada a mesada de Artur (A) resulta em R$ 810,00. Assim, chegamos a nossa primeira equação:
C + A = 810Â Â (eq. 1)
Sabemos tambÊm que Carlos gastou R$ 8,00 a mais do que Artur. Desta forma, podemos dizer que o gasto de Carlos menos o gasto de Artur resulta em R$ 8,00. Como Carlos gastou 2/3 e Artur gastou 3/5 da mesada, podemos representar essa diferença entre os gastos na forma de equação da seguinte maneira:
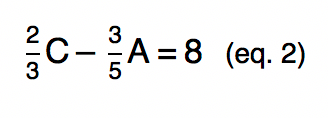

Podemos representar matematicamente um contexto em que foi gasto uma fração de um certo valor atravÊs do produto dessa fração pelo valor total. Carlos gastou 2/3 de sua mesada, cujo valor total nós determinamos que Ê C. Artur gastou 3/5 do total de sua mesada, cujo valor determinamos ser A. Por isso, temos na equação acima 2/3 multiplicando C e 3/5 multiplicando A.
Ficou claro, pessoal? EntĂŁo, vamos resolver o caso! Montamos duas equaçþes e temos 2 incĂłgnitas, A e C. Isso significa que jĂĄ ĂŠ possĂvel encontrar a solução do problema. Começaremos isolando a incĂłgnita A da equação 1 e substituindo o valor encontrado na equação 2.
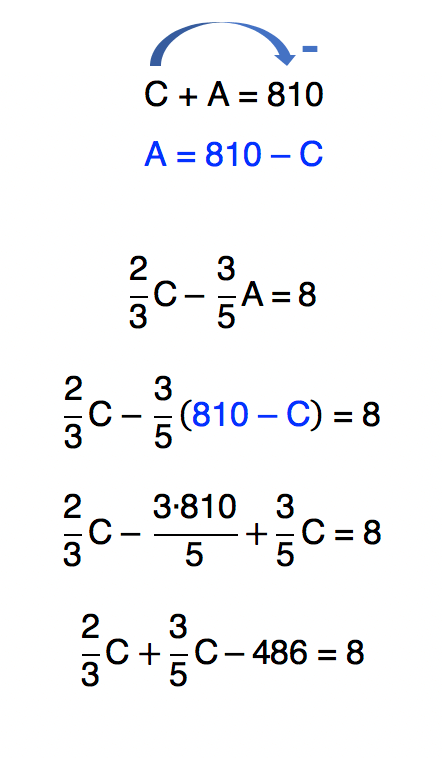
Reparem que ao substituirmos o valor de A na segunda equação, precisamos aplicar a propriedade distributiva e organizar os termos. Agora, como estamos trabalhando com fraçþes, nĂŁo poderĂamos escapar do cĂĄlculo do MMC, nĂŁo fosse o seguinte detalhe: os denominadores das fraçþes sĂŁo nĂşmeros primos! Assim, efetuando a multiplicação entre 3 e 5, chegamos ao denominador comum, 15.
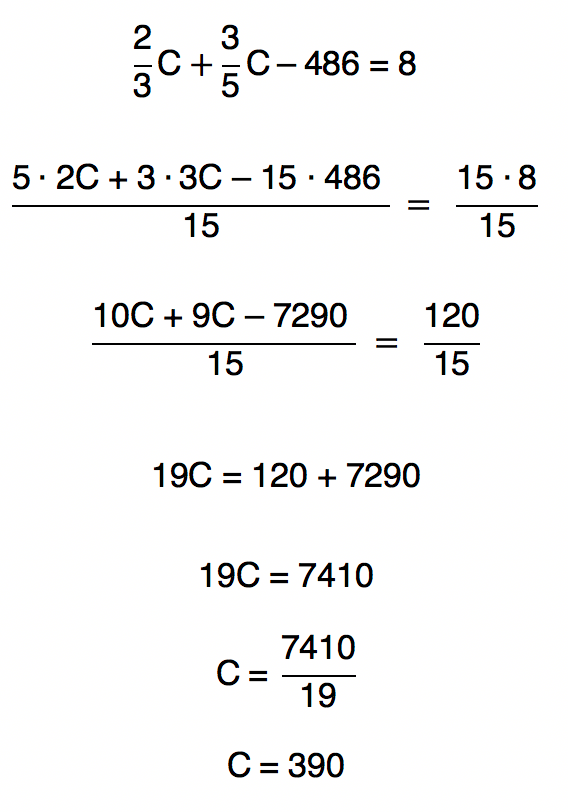
Agora que descobrimos o valor da mesada de Carlos, podemos descobrir a de Artur voltando a qualquer uma das equaçþes. Para facilitar nosso trabalho, voltaremos a equação 1:
A = 810 â 390
A = 420
IncrĂvel, nĂŁo ĂŠ? Mas calma que ainda nĂŁo chegamos ao resultado final. A questĂŁo quer saber o valor monetĂĄrio da diferença entre os valores das duas mesadas, logo:
420 â 390 = 30
Assim, a diferença entre os valores das mesadas de Carlos e Artur Ê de R$ 30,00.
Colocando-se 24 litros de combustĂvel no tanque de uma caminhonete, o ponteiro do marcador, que indicava 1/4 do tanque, passou a indicar 5/8. Determine a capacidade do tanque de combustĂvel da caminhonete.
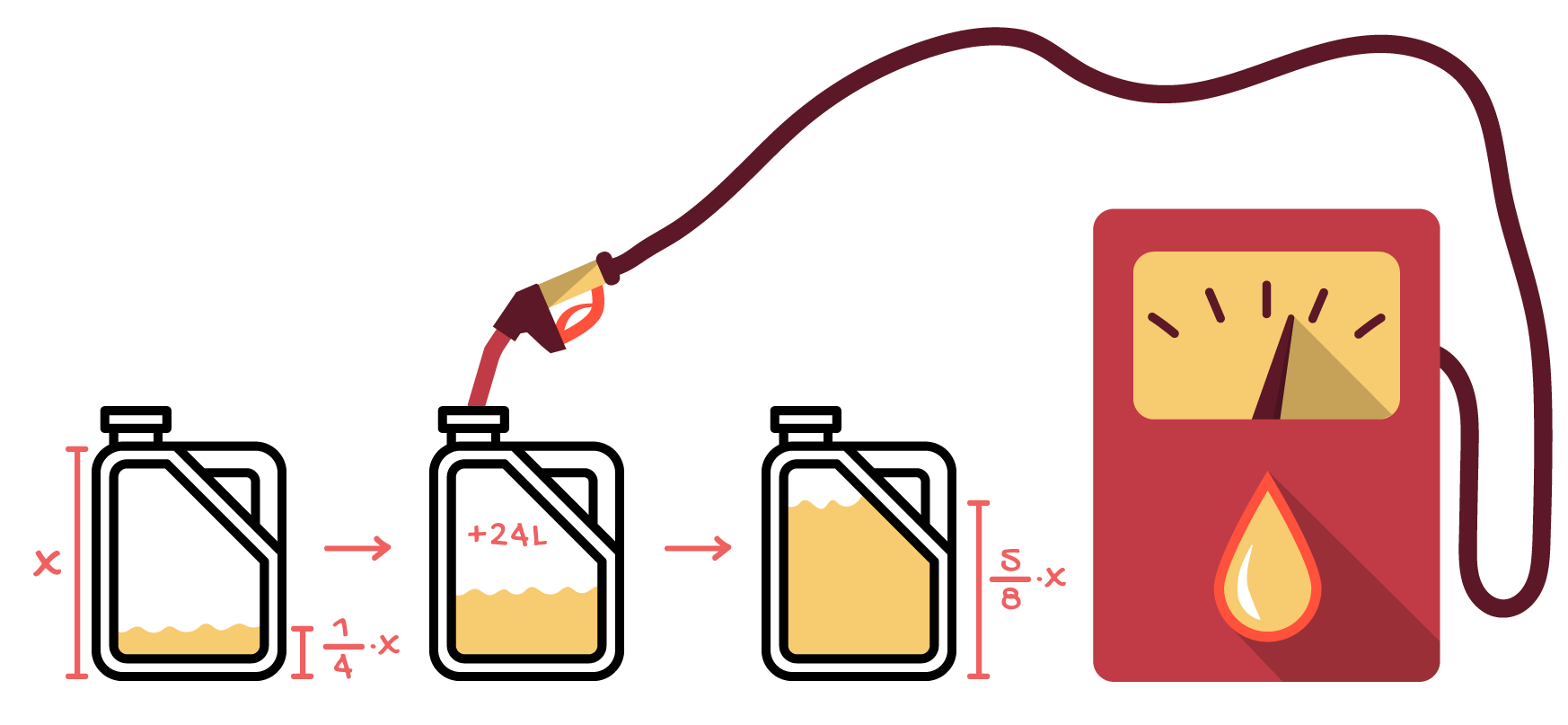
Novamente, para equacionarmos a situação apresentada no problema, precisamos utilizar a dica ninja que foi dada neste texto. Podemos representar matematicamente um contexto em que se fala de uma fração de um certo valor atravĂŠs do produto dessa fração pelo valor total. Ora, se considerarmos que a capacidade total do tanque ĂŠ de x litros, antes de colocar os 24 litros descritos no enunciado, o tanque possuĂa Âź dos x litros totais. Depois que os 24 litros foram adicionados, o tanque ainda nĂŁo encheu, mas ficou com 5/8 da capacidade total, que ĂŠ x. Deste modo, em forma de equação, podemos dizer que:
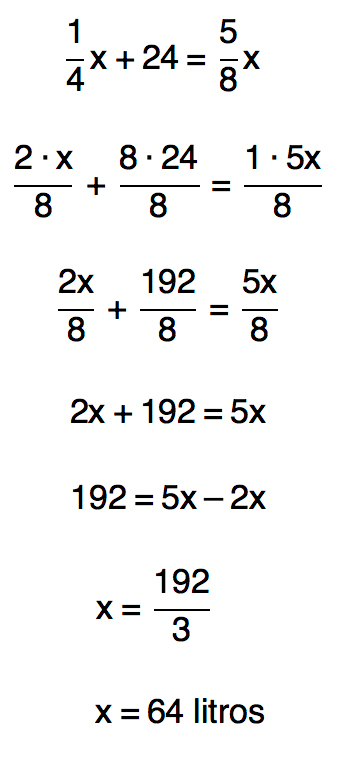
Assim, finalizamos o texto de hoje! Espero que depois de termos visto todos esses conceitos, as equaçþes do primeiro grau nĂŁo sejam mais um mistĂŠrio para vocĂŞs! TambĂŠm estou deixando um vĂdeo em anexo, logo abaixo. Quem assistir, resolverĂĄ comigo diversas outras equaçþes para praticar bastante o assunto!
Ahh… e se vocĂŞ curtiu este texto, aproveite para conhecer a plataforma do Professor Ferretto. Clique aqui para saber como a plataforma funciona!
Deseja ter uma preparação completa em matemåtica e ciências da natureza? Então conheça os planos e cursos da plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!
Um abração, sucesso e atÊ o próximo texto!
