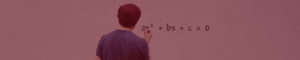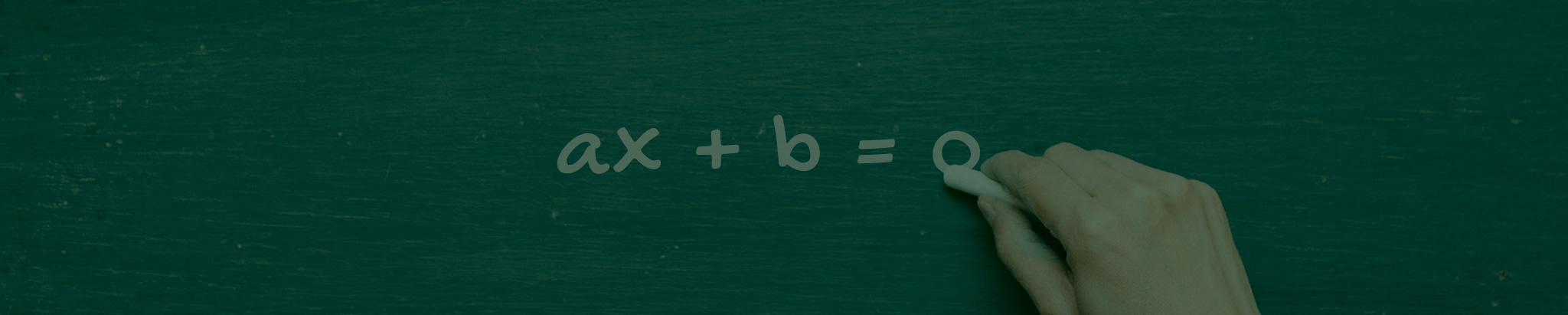PRODUTOS NOTÁVEIS: DE ORDEM 2

Olá pessoal! Como vão?

Se algo é notável, significa que merece ser apreciado, percebido, e que é digno de nota e de atenção. Então, por que não estudar os produtos notáveis? Produtos, na matemática, representam multiplicações, por isso podemos dizer que os produtos notáveis são multiplicações de expressões algébricas cujo resultado é uma forma conhecida. Assim, a ideia é utilizar os produtos notáveis para simplificar facilmente as expressões algébricas, ao invés de resolvê-las passo a passo, garantindo uma resolução rápida, e tempo é algo muito válido quando realizamos, por exemplo, as provas do ENEM e dos vestibulares!

E se vocês desejam aprender mais sobre matemática básica, ou sobre os demais conteúdos de matemática do ensino médio, para não perder tempo nas provas que irão realizar, então assinem a plataforma do Professor Ferretto! Lá vocês podem montar o seu próprio plano de estudos para se organizar direitinho, e tem acesso a um acervo de mais de 990 questões do ENEM e dos vestibulares para resolver, sem falar nos simulados semanais, onde o tempo é crucial na resolução das questões! Acessem o site e saibam mais!

Agora, vamos ao que interessa! Estudaremos nesse texto, três dos produtos notáveis existentes, apenas aqueles que geram um polinômio de ordem 2, ou seja, cujo termo de maior grau do resultado terá expoente 2. Acompanhem comigo aqui!

 

1. QUADRADO DA SOMA ENTRE DOIS TERMOS

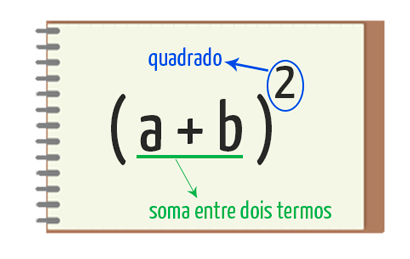
Observem a imagem acima com atenção, e vocês entenderão porque esse produto notável se chama quadrado da soma entre dois termos, no caso a e b. Aí vocês poderiam se perguntar: certo, mas o produto notável não era para ser um produto, porque temos a presença de uma potência? O fato é que quando elevamos um termo ao quadrado, significa que estamos multiplicando esse termo por ele mesmo! E é desenvolvendo essa multiplicação através do uso da propriedade distributiva, ou do famoso chuveirinho, que chegamos ao resultado do produto notável em questão, vejam só:

Assim, nós podemos concluir que:

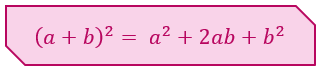
Se nós adotarmos o valor de a como sendo o primeiro termo, e o valor de b como o segundo termo, poderemos ler e memorizar a expressão da seguinte maneira:

“O quadrado do primeiro, mais duas vezes o primeiro vezes o segundo, mais o quadrado do segundo”

Certo pessoal!? É muito importante que vocês tenham sempre em mente a frase que acabamos de aprender, afinal conhecer ela será a garantia de que vocês sempre lembrarão da fórmula deste produto notável. Vamos agora ao próximo produto!

   

2. QUADRADO DA DIFERENÇA ENTRE DOIS TERMOS

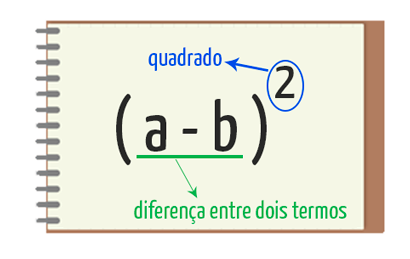
Podemos observar na imagem acima, que esse segundo produto notável é muito semelhante ao primeiro. O que muda, na verdade, é a operação a se realizar entre os dois termos a e b, que antes era uma soma, e agora é uma subtração, o que explica o nome: quadrado da diferença entre dois termos. Por isso, vamos utilizar a mesma ideia para encontrar seu resultado, ou seja, de que há uma multiplicação do termo “a – b” por ele mesmo, olhem só:

Assim, nós podemos concluir que:

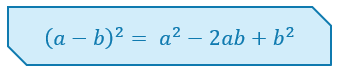
E mais uma vez, considerando a como o primeiro termo, e b como o segundo termo, poderemos ler e memorizar o resultado da seguinte maneira:

“O quadrado do primeiro, menos duas vezes o primeiro vezes o segundo, mais o quadrado do segundo”

Como já ressaltamos, é tamanha a semelhança entre os dois produtos notáveis que acabamos de ver. Desta forma, é possível tirar proveito desse fato, e fazer a seguinte associação:

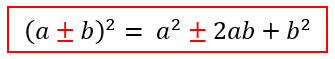
Reparem que o único sinal que muda, entre uma expressão e outra, é o sinal do segundo termo do resultado do produto do notável, e para a nossa sorte, ele acompanha a operação realizada dentro do parênteses do produto. Portanto, é só lembrar do seguinte: se tivermos um caso de um quadrado da soma entre dois termos, o sinal do segundo termo do resultado será positivo. Do contrário, ou seja, se tivermos um caso de um quadrado da diferença entre dois termos, então o sinal do segundo termo do resultado será negativo. Pronto!

 

3. PRODUTO DA SOMA PELA DIFERENÇA

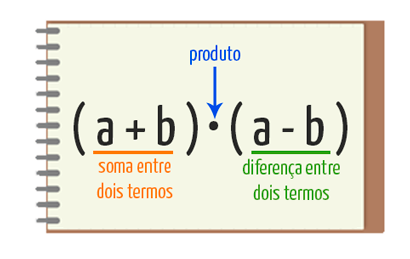
Analisando a imagem acima, fica mais claro para nós porque o produto notável em questão é chamado de produto da soma pela diferença. Mas o mais interessante desse caso, é o resultado que vamos obter aplicando a propriedade distributiva na expressão. Observem com atenção:

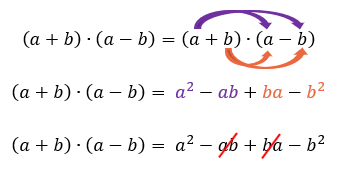
Assim, chegamos a seguinte conclusão:

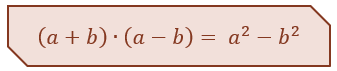
Incrivelmente, nesse caso, nós conseguimos cancelar dois termos da expressão, por isso, denominando a e b como primeiro e segundo termos da soma e da diferença, respectivamente, poderemos ler e memorizar o resultado da seguinte maneira:

“O quadrado do primeiro, menos o quadrado do segundo”

Simples não é? Agora, para não nos confundirmos quanto a aplicação de cada um dos produtos notáveis, vamos resolver uma série de exercícios. Vem comigo aqui!

Observem que temos um termo ao quadrado para resolver. Por isso, certamente não se trata do 3º produto notável que aprendemos hoje. Assim, é necessário reparar na operação entre os termos dentro do parênteses. Opa, se trata de uma soma! Então…

 

Vejam que nesse caso, não temos a presença de termo algum elevado ao quadrado. Isso só pode significar que estamos tratando do 3º produto notável, olhem só!

 

Agora, encontramos mais um caso em que temos a presença de um termo elevado ao quadrado, contudo, vejam que dessa vez a operação entre os termos dentro do parênteses é uma subtração! Assim, chega a hora de aplicarmos o 2º produto notável de hoje:

Tudo tranquilo até aqui? Neste momento, nós iremos trabalhar em um exercício um pouquinho mais complexo, mas não tão difícil quanto parece, acompanhem!

 

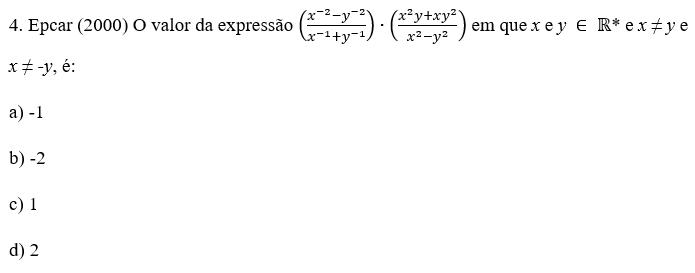
Gostaram da expressão? Se vocês a observarem com atenção, poderão perceber que precisaremos inverter as potências que possuem expoente negativo, e que poderemos colocar alguns termos comuns em evidência, além do fato de já existir um produto notável evidente entre os termos. Conseguiram visualizar? Se não, atentem a figura abaixo:

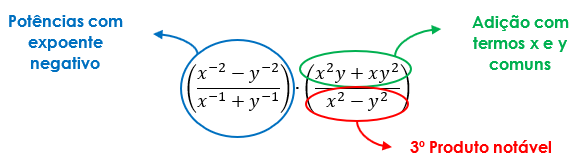
Assim, nos resta realizar todos esses passos descritos acima. Vem comigo aqui!

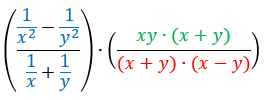
Observem que na primeira parcela do produto, será necessário realizar o mínimo múltiplo comum ou MMC, no numerador e no denominador da fração. Para isso, faremos a multiplicação dos denominadores de cada uma das frações que irão somar-se ou subtrair-se. Por sua vez, na segunda parcela do produto, já encontramos termos iguais no numerador e no denominador da fração, e por isso, poderemos efetuar alguns cancelamentos.

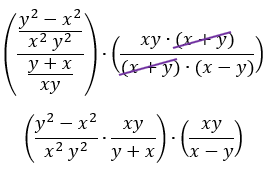
Neste momento, chegamos em um ponto onde temos um grande produto de 3 frações. Isso é muito interessante, pois nos permitirá fazer mais alguns cancelamentos, e ainda, se ficarmos bem atentos, poderemos perceber a presença de novos produtos notáveis! Acompanhem esses desdobramentos:

Parece que chegamos a um resultado, contudo resta um problema. Se nós voltarmos ao enunciado do exercício, veremos que temos 4 alternativas com resultados numéricos. Só que o nosso resultado ainda é algébrico. O que fazer então?

Se vocês voltarem os olhos para a nossa fração, perceberão que o numerador é exatamente o oposto do denominador, ou seja, no numerador o termo x² é negativo, enquanto que no denominador o mesmo termo é positivo. Algo parecido acontece com o termo y², já que no numerador ele é positivo enquanto que no denominador ele é negativo. Para resolver esse impasse sem alterar a equação original, basta que coloquemos o sinal negativo do numerador em evidência, ou ainda, que multipliquemos o numerador por “-1”. Assim, teremos a seguinte situação:

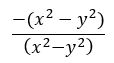
Um pouco melhor não é? Agora é possível perceber que as subtrações dentro dos parênteses são exatamente iguais, e que por isso poderemos cancelar os termos!

 

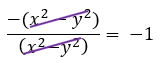
E assim chegamos ao final de mais um texto! Ficarei bastante feliz se o conteúdo apresentado aqui for proveitoso para os seus estudos, e se os exercícios resolvidos lhes derem um apoio quando vocês tiverem dúvidas ao resolverem outras questões. Deixo em anexo o vídeo que aborda esse assunto de forma complementar ao texto. Deem uma olhada nele, e sigam firmes nos estudos!

Grande abraço pessoal! Nos vemos em breve!