MÍNIMO MÚLTIPLO COMUM E SUAS PROPRIEDADES

Olá pessoal, tudo bem com vocês?

No texto de hoje vamos aprender sobre um assunto muito importante que é o MMC, ou seja, o mínimo múltiplo comum. Este é um assunto que muitas vezes é cobrado no ENEM e em muitos vestibulares, por isso é muito importante que vocês saibam exatamente do que se trata.

Antes de começar, uma dica muito importante: assine a plataforma Professor Ferretto. Na plataforma você terá acesso a videoaulas, exercícios resolvidos, material didático e muito mais sobre a matemática essencial para o ENEM e para os vestibulares em geral. Assine lá! Certo pessoal? Então, vem comigo aqui!

O mínimo múltiplo comum é também conhecido pelas siglas iniciais do seu nome, ou seja, o MMC. Para começarmos a falar sobre o MMC, é importante a gente entender a ideia de múltiplo, ou seja, o que significa um número ser múltiplo de outro número.

Por exemplo, vamos escrever quais são os números múltiplos de 4:

(4, 8, 12, 16, 20, 24, ….)

Agora, por exemplo, os números múltiplos de 5:

(5, 10, 15, 20, 25, 30, ….)

Pessoal, o importante aqui é que vocês percebam o seguinte, do 4 para o 8, está sendo acrescentado 4. Assim, podemos ver que os números múltiplos de 4 vão crescendo de 4 em 4. Notem que o mesmo acontece com os números múltiplos de 5, ou seja, eles vão crescendo de 5 em 5.

Agora que já temos uma ideia de múltiplo, nós iremos aprender como encontrar o MMC entre dois ou mais números. Vamos determinar o MMC entre o 2 e o 3, como exemplo. Para isto, vamos fazer o conjunto dos números múltiplos de 2 e também o conjunto dos múltiplos de 3.

M (2) = (2, 4, 6, 8, 10, 12, 14, …)

M (3) = (3, 6, 9, 12, 15, 18, …)

O que acontece aqui é o seguinte, a gente tem 2 conjuntos sendo representados, um deles representando os múltiplos do 2 e o outro representando os múltiplos do 3. Mas, eles têm elementos em comum no seus conjuntos. Olhem só, nós temos o 6 como elemento comum, ou seja, podemos dizer que o 6 é múltiplo tanto de 2 como de 3. Assim, o 6 é múltiplo comum entre o 2 e o 3. Vejam que existem outros números que são múltiplos comuns entre 2 e 3, como o 12 e o 18, por exemplo.

Fazendo essa representação conseguimos determinar os múltiplos comuns entre 2 e 3. No entanto, como a ideia é aprender o mínimo múltiplo comum entre eles, ou seja, o menor múltiplo comum, podemos ver que este número é o 6. E ainda, vocês podem perceber que se a gente for pulando de 6 em 6, vamos ter os múltiplos que são comuns entre o 2 e o 3.

Desta forma:

MMC (2, 3) = 6

Reparem que o entendimento do que é o múltiplo de um número é fundamental. O problema é que não temos como, em uma questão por exemplo que envolva mínimo múltiplo comum, fazer essa construção de número em número até encontrarmos o menor múltiplo comum, isto seria muito trabalhoso. É por isso, que para encontrar o mínimo múltiplo comum entre dois ou mais números existe uma regra, ou um método, que é o método da decomposição simultânea em números primos. Esse método está totalmente vinculado a fatoração.

1. DECOMPOSIÇÃO SIMULTÂNEA EM NÚMEROS PRIMOS

Vamos começar fazendo um exemplo, o MMC entre 8 e 12. Então, existe uma maneira mais simples de encontrar o MMC entre dois ou mais números. Essa maneira é a decomposição simultânea. Para fazer isso, a gente coloca 8 e o 12 um do lado do outro, passa um traço do lado de ambos e vai fatorando eles com números primos, inseridos do lado direito desse traço. Vamos começar com o menor número primo, que é o 2:

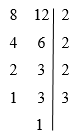
Dessa forma, você vai dividindo por 2 até que pelo menos um dos números possa ser dividido por 2. Quando um dos números não é divisível por 2, apenas copiamos ele. Assim, vamos dividindo por números primos maiores até que as colunas acabem em 1. Chegando nesse ponto, a decomposição acabou. Então, podemos calcular o mínimo múltiplo comum apenas multiplicando os números primos encontrados ao lado do traço.

Neste caso:

MMC (8, 12) = 2 . 2 . 2 . 3 = 24

Assim, o 24 é o MMC entre o 8 e o 12. Esse método da decomposição, ele pode ser usado com dois números, três números, e assim sucessivamente.

Vamos ver agora algumas propriedades que envolvem o mínimo múltiplo comum entre os números.

2. PROPRIEDADES

1° propriedade: o MMC entre 2 ou mais números primos, será sempre igual ao produto entre eles. Por exemplo:

MMC (3, 5) = ambos são números primos, então nem precisa fazer a decomposição, basta multiplicar eles, o MMC entre eles será 15.

2° propriedade: dados dois ou mais números em que o maior é múltiplo dos outros, o MMC é o maior número.

Olhem o exemplo:

MMC (4, 8) = 8 é múltiplo de 4, então o MMC será 8.

MMC (2, 8, 24) = o 24 é múltiplo de 2, e também é múltiplo de 8, então 24 será o MMC.

3° propriedade: Nessa propriedade, quando sabemos o MMC entre dois ou mais números, ao multiplicarmos todos por um número inteiro qualquer, o MMC dos números inicias também será multiplicado pelo número que você multiplicou, podemos encontrar o MMC do novo conjunto de números, apenas multiplicando o MMC por esse número também. Veja o exemplo.

MMC (8, 12) = 24

Multiplicando tudo por 5: 

MMC (40, 60) = 120

Lembrando pessoal, que isso vale para divisão também. Vamos fazer agora um exercício para que fique mais claro o entendimento para vocês! Vamos à ele!

Dois sinais luminosos acendem juntos num determinado instante. Um deles permanece aceso 1 minuto e a pagado 30 segundos, enquanto que o outro permanecesse aceso 1 minuto e apagado 20 segundos. A partir desse instante qual o número mínimo de minutos necessários para que os dois sinais voltem a acender juntos outra vez? Assinale no cartão de respostas o número da alternativa que contém a resposta que você calcular como correta.

01) Oito
02) Dez
04) Doze
08) Quatorze

O primeiro fica aceso 60 segundos mais 30 segundos apagado, ou seja, ele demora 90 segundos para acender novamente. Já o segundo fica 60 segundos aceso mais 20 desligado, ou seja, ele leva 80 segundos para acender novamente.

Então, nós precisamos encontrar um número que seja múltiplo dos dois, do 90 e do 80, para encontrarmos o número mínimo de minutos para eles acenderem juntos novamente:

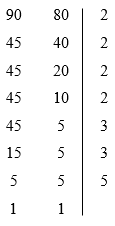
Desta forma, o MMC entre 90 e 80 é:

MMC (90, 80) = 2 . 2 . 2 . 2 . 3 . 3 . 5 = 720

Isto quer dizer que de 720 segundos em 720 segundos os sinais voltam a acender novamente juntos. No entanto, a questão pede o resultado em minutos, logo:

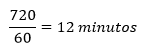
Ou seja, a cada 12 minutos eles voltam a acender juntos. Então, o item 04 é a alternativa correta. Fácil né!

Chegamos ao final de mais um texto e eu espero que tenha sido muito proveitoso para vocês e que ajude muito nos seus estudos. Deixo em anexo o vídeo sobre o conteúdo aprendido de MMC, pra que vocês possam acompanhar melhor as explicações.

Um abração, sucesso e até o próximo texto!