Os números irracionais são números decimais não exatos, que possuem representação infinita e não periódica e que não podem ser escritos como frações. Da união do conjunto dos números irracionais com o conjunto dos números racionais surge o conjunto dos números reais.

 

Olá, pessoal! Como vão?

Estamos aqui hoje para estudar algumas características que levam números como √2, √3, ou mesmo o número π a pertencerem a um conjunto numérico completamente distinto dos números racionais: o conjunto dos números irracionais! Vamos começar compreendendo a origem dos números irracionais e a sua definição! Em seguida, aprenderemos tudo sobre o conjunto dos números reais, aquele que veio para unir esses dois conjuntos tão diferentes. Por fim, é claro, vamos praticar o assunto através de uma questão de vestibular.

Legal, não é, pessoal? Quem quiser arrasar nas provas do ENEM e dos vestibulares está convidado a seguir comigo. Vamos lá!

 

1. ORIGEM DOS NÚMEROS IRRACIONAIS

Todos os conjuntos numéricos que conhecemos hoje surgiram para suprir alguma necessidade do ser humano. O conjunto dos números naturais, por exemplo, nasceu quando se percebeu a necessidade de expressar quantidade. Um pouco mais tarde, notou-se que ao subtrair de um número um valor maior do que ele, obtinha-se um resultado negativo. Foi aí que surgiu o conjunto dos números inteiros.

Contudo, nem os números naturais e nem os números inteiros conseguiam representar partes de um todo. Por isso, foi necessário criar o conjunto dos números racionais, composto pelos decimais exatos e as famosas dízimas periódicas. Como os números naturais, os inteiros, os decimais exatos e as dízimas periódicas podem ser representados na forma de fração, diz-se que todos pertencem ao conjunto dos números racionais.

Até um determinado momento, pensava-se que distribuindo todos os números racionais em uma reta real, e calculando a média aritmética entre os termos vizinhos, seria possível chegar a infinitos números racionais, que formariam todos os números existentes.

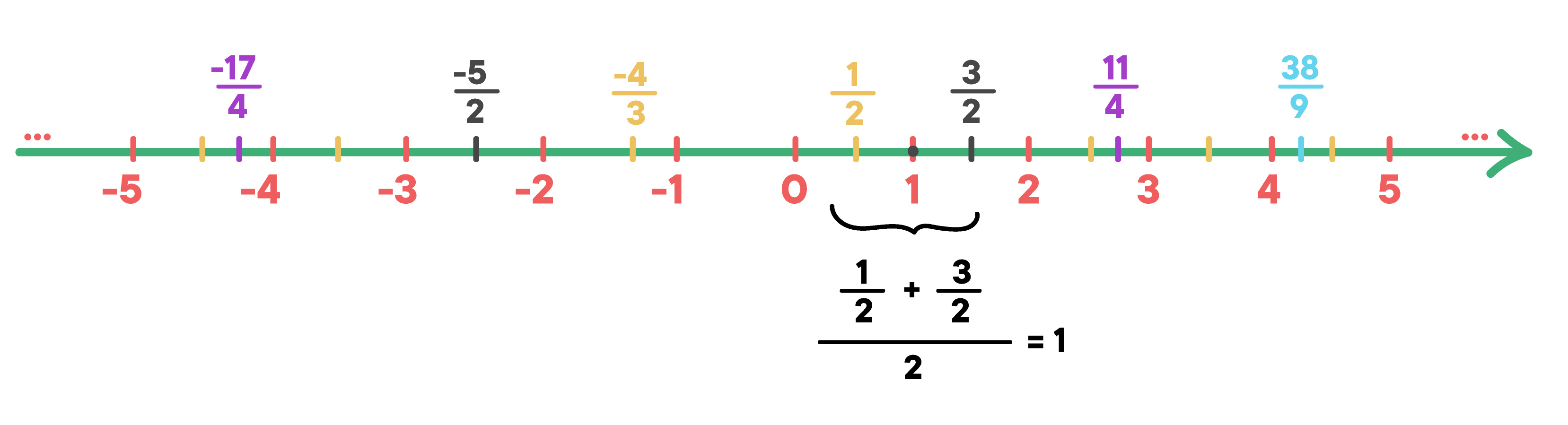
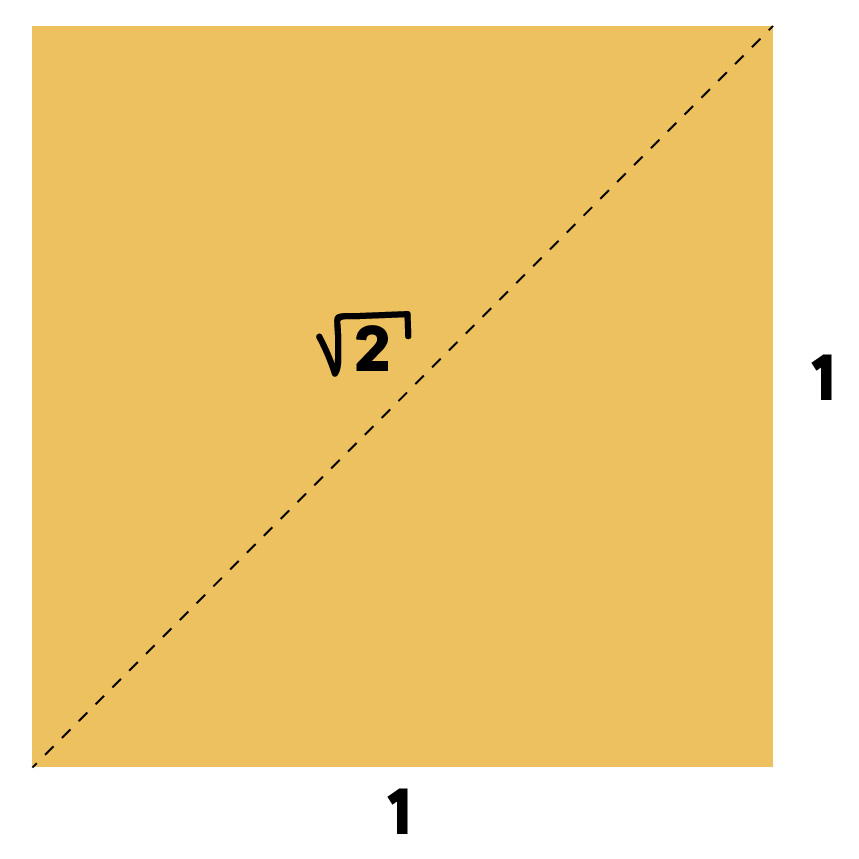
Entretanto, por mais que fossem realizadas infinitas médias aritméticas entre os números racionais, a reta real jamais seria composta por todos os números existentes. Restariam algumas lacunas, deixadas pelos números que não podem ser representados por frações. Esse “problema” ficou ainda mais evidente na geometria plana.

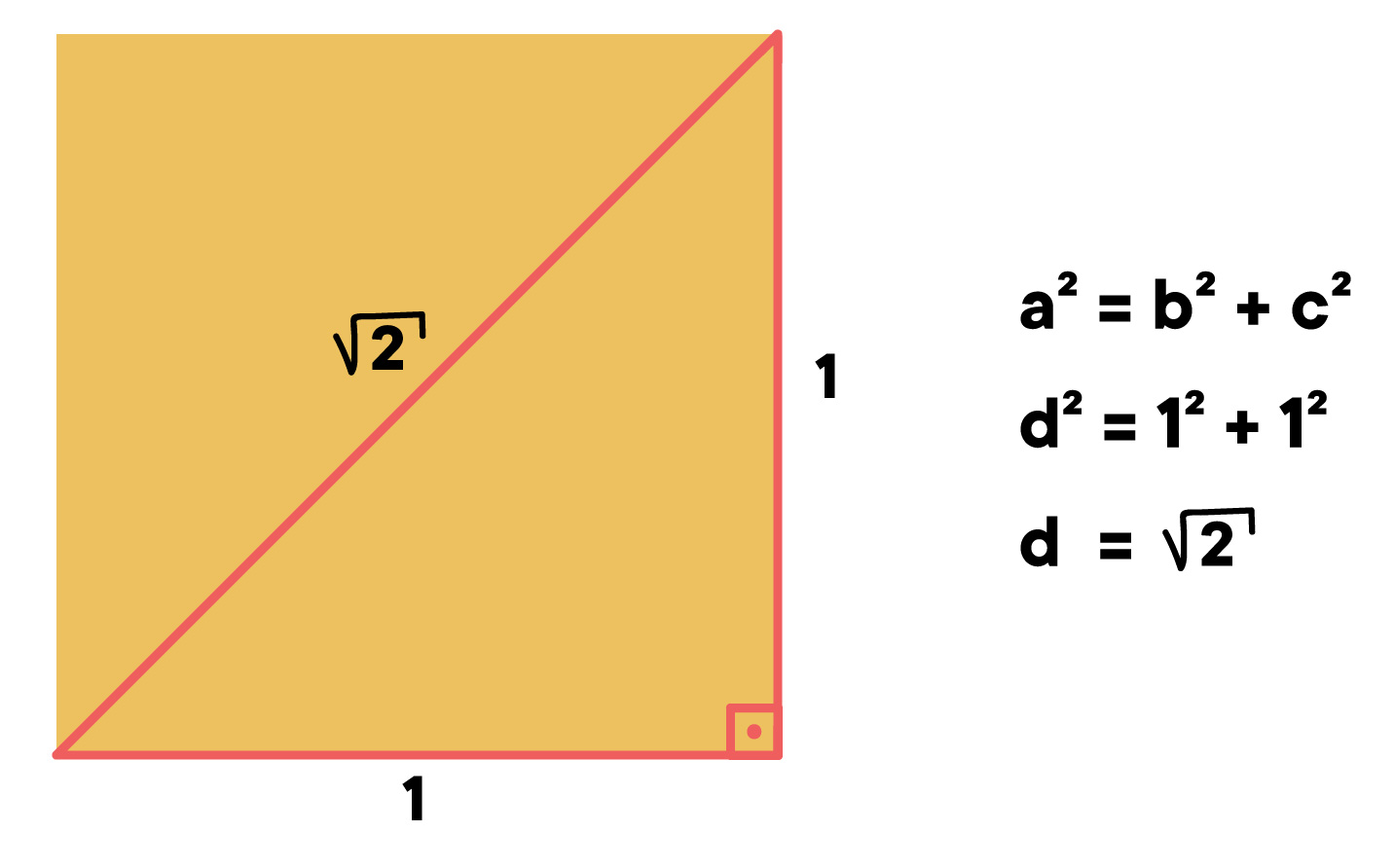
Ao calcular a diagonal de um quadrado de lado 1 através do Teorema de Pitágoras, por exemplo, obtém-se como resultado a raiz quadrada de um número primo. Só que números como esse não podem ser representados por uma fração. Assim, esse e outros questionamentos deram origem, mais tarde, a um novo conjunto numérico: o conjunto dos números irracionais. Vamos estuda-lo com detalhes na sequência. Vem comigo!

 

2. CONJUNTO DOS NÚMEROS IRRACIONAIS

Como vimos logo no início do texto, os números irracionais são números decimais não exatos, que possuem representação infinita e não periódica e que também não admitem ser escritos como frações com numerador e denominador inteiros. Para compreendermos essa definição com clareza, vamos analisar alguns números irracionais.

√2 = 1,41421356237309504880168872…

√3 = 1,73205080756887729352744634…

Reparem nos números irracionais acima, que as casas decimais não terminam, são infinitas e completamente aleatórias. Isso significa que não há uma periodicidade ou uma sequência entre os algarismos dispostos após a vírgula, e que também não há como saber quais algarismos compõem as casas decimais representadas pelas reticências. Essas incertezas sobre o comportamento das casas decimais dos números irracionais nos impedem de representa-los sob a forma de fração.

Assim, podemos afirmar, por exemplo, que todas as raízes quadradas extraídas de números que não são quadrados perfeitos são números irracionais. Outro bom exemplo de número irracional é o famoso “pi” (π). Seu valor numérico possui infinitas casas decimais, sem que haja qualquer periodicidade entre os seus algarismos. O valor de π é oriundo da razão entre o comprimento de uma certa circunferência e o seu diâmetro.

π = 3,14159265…

 

2.1 O conjunto dos números irracionais em forma de diagrama

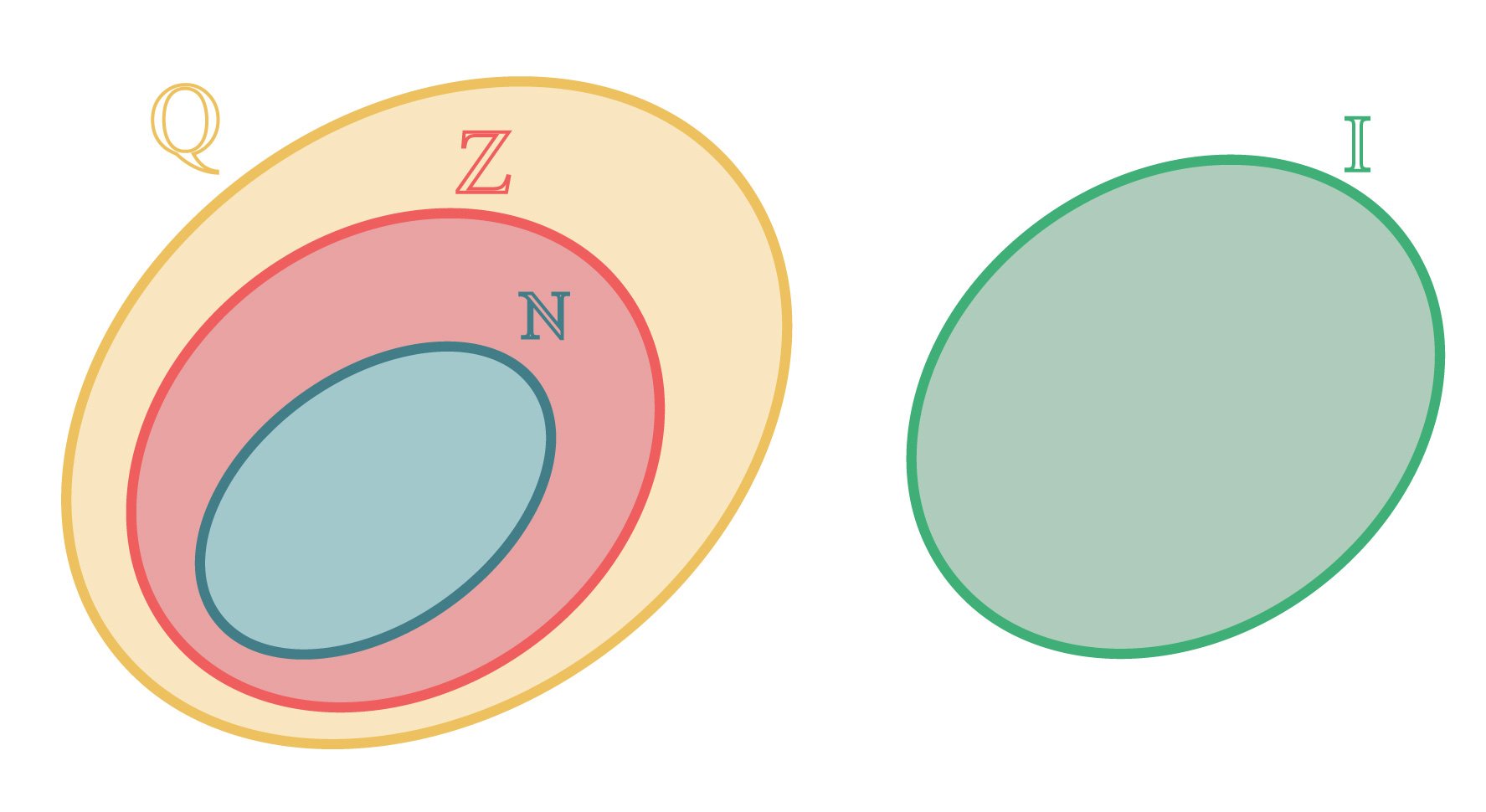
No decorrer deste texto, nós estudamos dois temas importantes dentro dos conjuntos numéricos. O primeiro deles, é que todos os números naturais e inteiros, assim como os decimais exatos e as dízimas periódicas são considerados números racionais. Isso nos permite concluir que os números naturais (ℕ) e os números inteiros (ℤ) são subconjuntos do conjunto dos números racionais (ℚ).

O segundo, e principal tema estudado aqui, é que o conjunto dos números irracionais (𝕀) é completamente diferente do conjunto dos números racionais. Esses dois conjuntos não possuem elementos em comum. Por isso, diz-se que eles são conjuntos disjuntos, e que a intersecção entre esses dois conjuntos resulta em um conjunto vazio.

ℚ ⋂ 𝕀 = ∅

De acordo com essas informações, podemos realizar a representação na forma de diagrama dos conjuntos apresentados como mostra a imagem acima. Mas e aí, vocês não estão sentindo falta de um conjunto nessa imagem? Nós vamos estudar o conjunto dos números reais no próximo item. Sigam comigo!  

 

3. CONJUNTO DOS NÚMEROS REAIS

O conjunto dos números reais (ℝ) é formado pela união entre o conjunto dos números racionais e o conjunto dos números irracionais. Assim, quando for necessário se referir a todos os números de maneira geral, sem excluir aqueles que podem ou que não podem ser representados na forma de fração, estaremos falando dos números reais.

ℝ = ℚ ⋃ 𝕀

ℝ = {x | x ∈ ℚ ou x ∈ 𝕀}

Dessa maneira, é possível completar a representação em forma de diagrama que realizamos no item anterior. Reparem que todos os demais conjuntos estudados estão localizados dentro do diagrama do conjunto dos números reais. Não podia ser diferente, afinal, números naturais, inteiros, racionais e irracionais também são números reais.

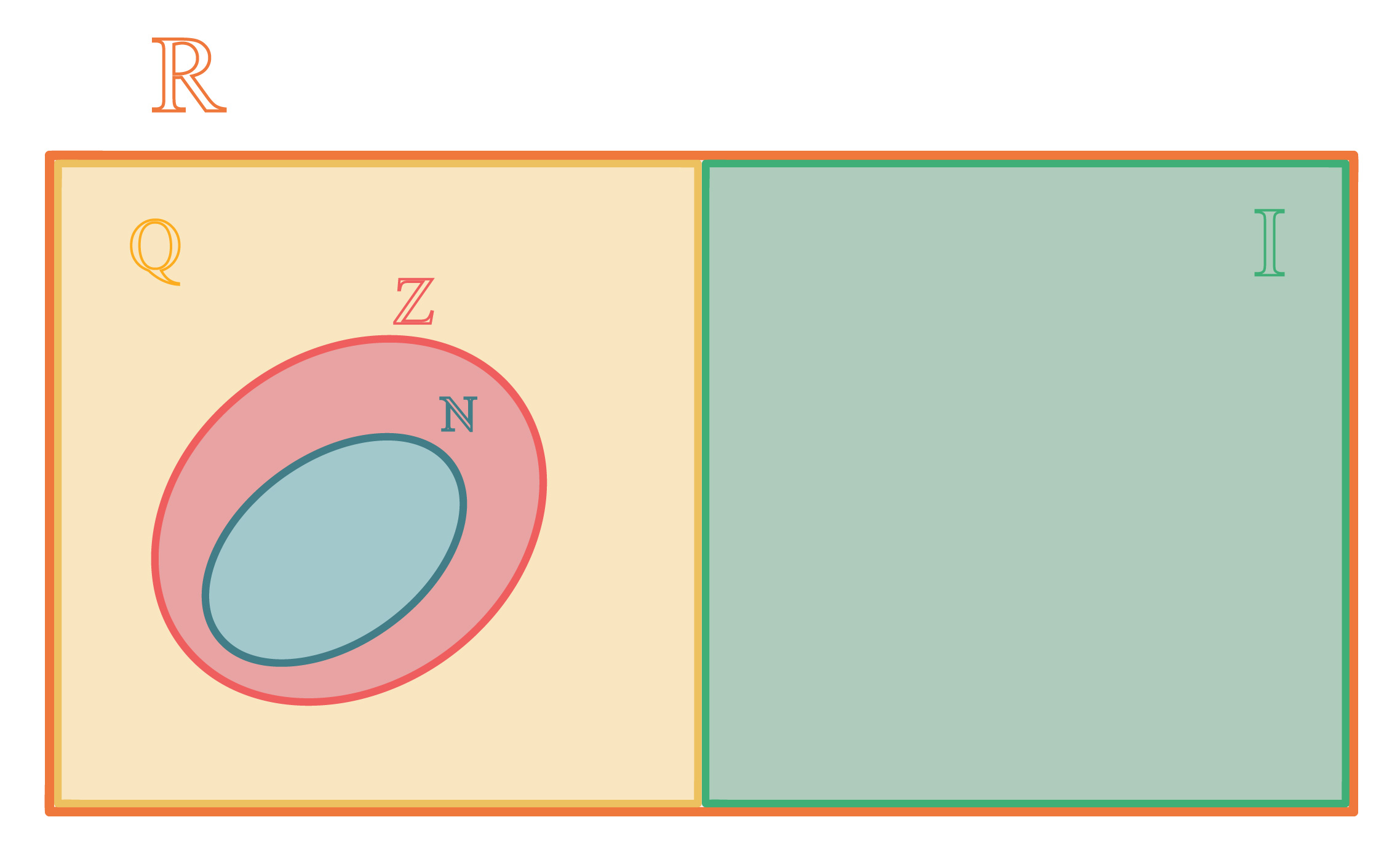
Além disso, com o advento dos números irracionais e reais, finalmente acabamos com as lacunas na reta real! Aliás, neste momento, o termo “reta real” ganha todo sentido. Se o conjunto dos números reais é formado por todos os números existentes, significa que podemos representar todo e qualquer número que desejarmos na reta. Com toda a certeza, esse número será racional ou irracional!

Certo, pessoal? Após adquirirmos todo esse conhecimento, nada melhor do que fechar o texto resolvendo um exercício. Vem comigo aqui!

 

4. EXERCÍCIO RESOLVIDO SOBRE OS CONJUNTOS NUMÉRICOS

(G1 – UTFPR) Indique qual dos conjuntos abaixo é constituído somente de números racionais.

a. {–1, 2, √2, π}
b. {–5, 0, ½, √9}
c. {–2, 0, π, ⅔}
d. {√3, √64, π, √2}
e. {–1, 0, √3, ⅓}

Pessoal, este exercício nos pede para determinar qual conjunto é composto apenas por números racionais. Portanto, se houver qualquer número irracional em alguma das alternativas, esta poderá ser descartada. Nesse sentido, aproveito para deixar a seguinte dica:

As vezes é mais fácil resolver uma questão descartando alternativas do que procurando exclusivamente a alternativa correta!

Entendido? Então, vamos analisar, um a um, os conjuntos apresentados.

a. {–1, 2, √2, π}

c. {–2, 0, π, ⅔}

d. {√3, √64, π, √2}

Reparem no ilustre elemento que pertence aos 3 conjuntos acima. O número π é um número irracional! Dessa forma, não é preciso analisar se os outros elementos de cada conjunto são ou não números racionais. Essas 3 alternativas já podem ser descartadas.

b. {–5, 0, ½, √9}

e. {–1, 0, √3, ⅓}

E agora, qual dos dois conjuntos possui apenas elementos racionais? Vocês poderiam pensar que nenhum deles, afinal, ambos possuem radicais, um indício de que sejam elementos irracionais. Mas se vocês repararem melhor, na alternativa b, temos a presença de uma raiz quadrada de um quadrado perfeito, o número 9. Isso resulta em um resultado inteiro, o número 3.

Já na alternativa e, temos a presença de uma raiz quadrada de um número que não é quadrado perfeito, mas sim, um número primo. Curiosamente, nós utilizamos o número √3 como exemplo de número irracional neste texto. Fim de papo, a alternativa correta é a letra b!

b. {–5, 0, ½, √9} 

 

Finalizando com chave de ouro!

Neste momento, acredito que vocês estão preparados para encarar todos os conjuntos numéricos, e por isso, fico por aqui! Não esqueçam de assistir o vídeo que está disponível logo abaixo! Ele complementa todo o estudo dos números irracionais e reais que acabamos de realizar.

E quem gostou do conteúdo, pode ficar à vontade para acompanhar todos os posts do blog, e claro, conhecer a plataforma do Professor Ferretto! Clique aqui para saber como ela funciona!

Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da Plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!

Um abração a todos e até breve!