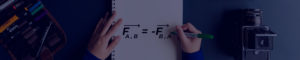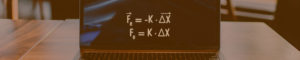Uma associação de molas é nada mais do que molas colocadas juntas para realizar determinada tarefa. Quando molas são colocadas de forma contínua, a associação é em série. Quando molas são dispostas paralelamente, a associação é paralela. De acordo com a forma da associação, teremos uma ou outra dureza equivalente.

 

Oi, pessoal! Tudo bem com vocês?

Ao trabalhar com a força elástica, a associação de molas é um recurso valioso. Através da associação, é possível modificar a dureza equivalente das molas de acordo com a necessidade. Aplicando a Lei de Hooke, conseguimos encontrar a relação entre as constantes elásticas e deduzir fórmulas para calcular a constante elástica equivalente da associação.

Prontos? Então, vamos lá!

 

1. LEI DE HOOKE

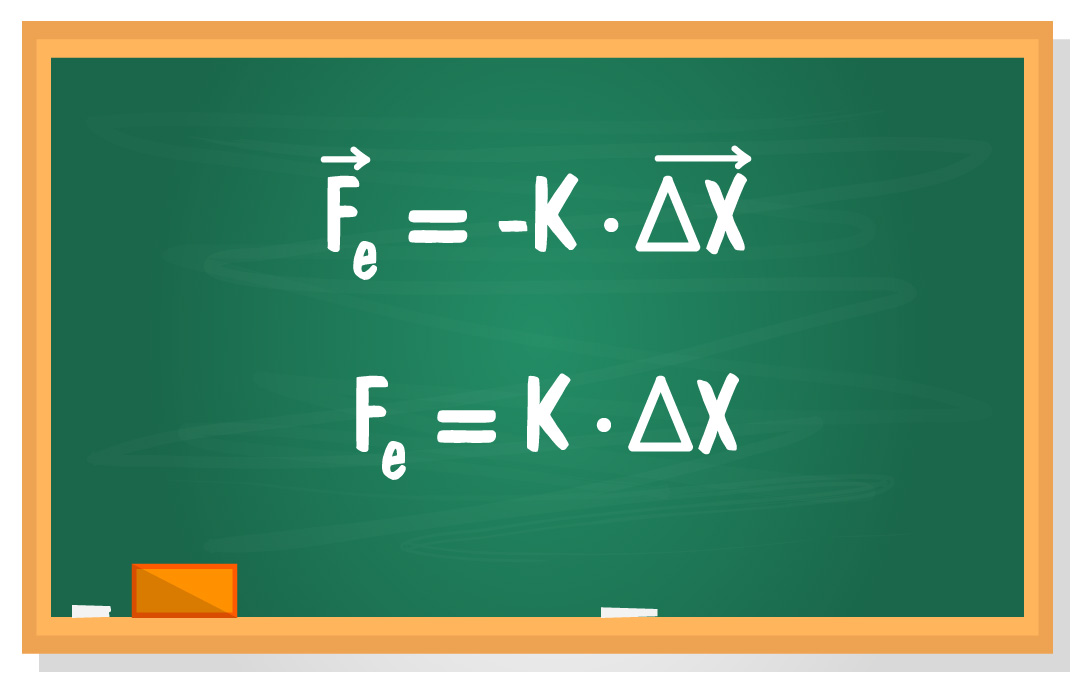
A Lei de Hooke, conforme apresentado no texto sobre força elástica, expressa a relação de proporcionalidade entre força e deformação de uma mola. A medida que define essa proporção é a dureza da mola, conhecida pelo nome de constante elástica. A força elástica é chamada de força restauradora pelo fato de sempre agir em sentido oposto à deformação:

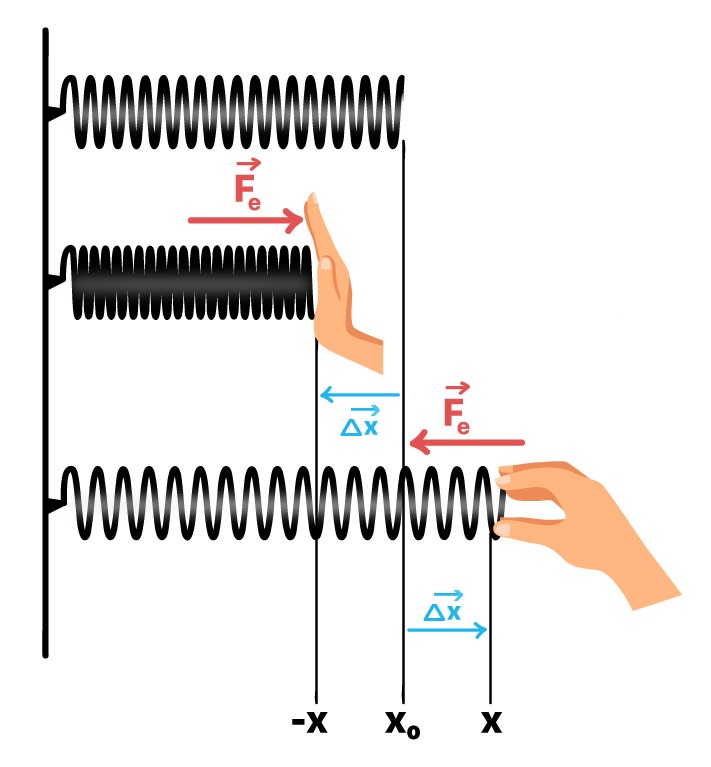
Tendo essa relação em mente, podemos calcular o valor da força elástica através do produto entre a constante elástica e o módulo da deformação da mola (lembrando que módulo é o mesmo que valor):

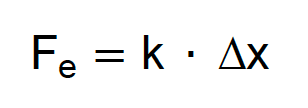
A aplicação dessa equação para uma mola única é simples. Como exemplo, uma mola de constante elástica k = 10 N/cm sofre uma compressão de 5 cm. Qual é a força elástica que essa mola exerce?

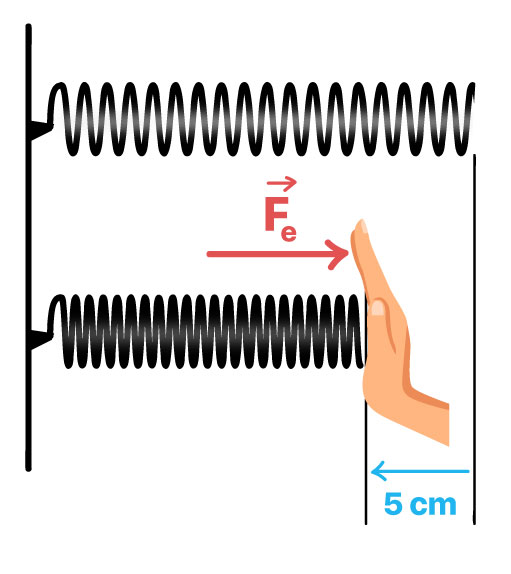
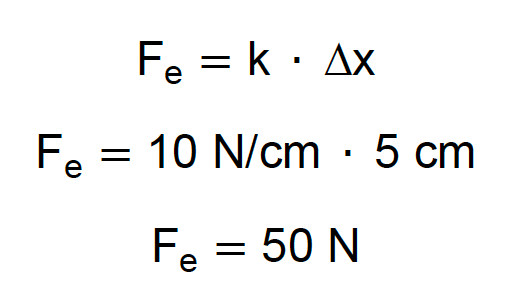
Perfeito, descobrimos que a força elástica exercida pela mola é de 50 N. Uma aplicação rápida da fórmula. Mas, esse exemplo trouxe apenas uma mola. O que aconteceria caso houvesse mais molas unidas, caso houvesse uma associação de molas? 

 

2. ASSOCIAÇÃO DE MOLAS EM SÉRIE

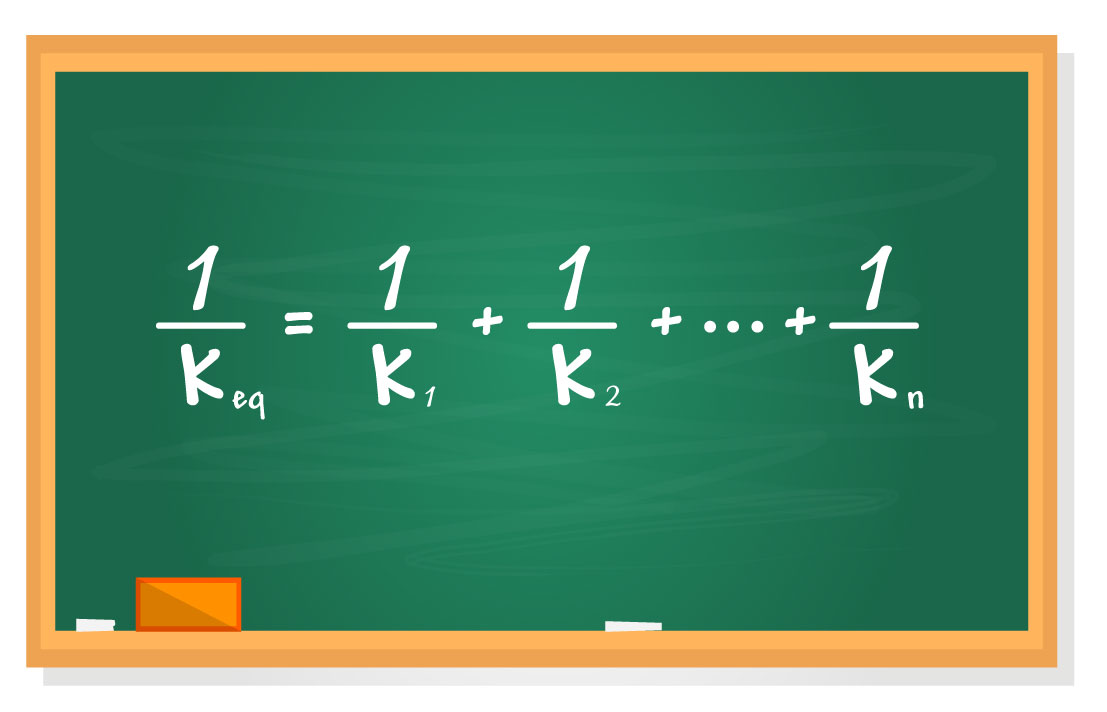
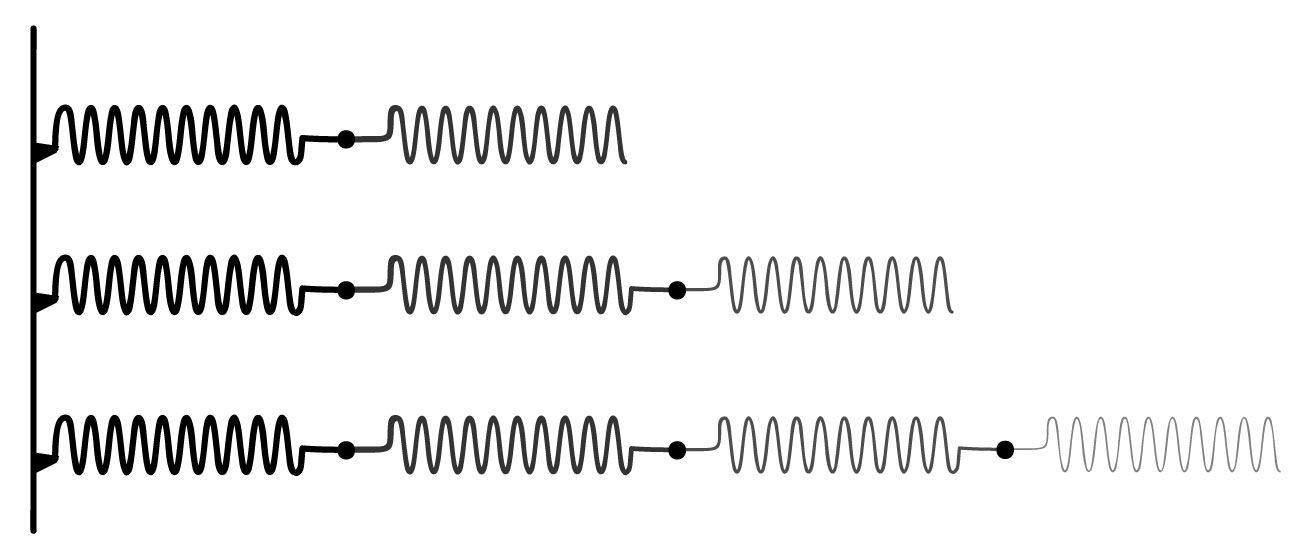
Primeiramente, o que seria uma associação de molas em série? Associar molas em série é simplesmente conectar uma após a outra. Na imagem abaixo, temos associação de duas, três e quatro molas, respectivamente:

Ao estudar situações assim, buscamos calcular uma constante elástica equivalente por toda a associação. É como se trocássemos as duas molas da primeira associação por uma única mola de natureza correspondente. Vejamos como isso se dá:

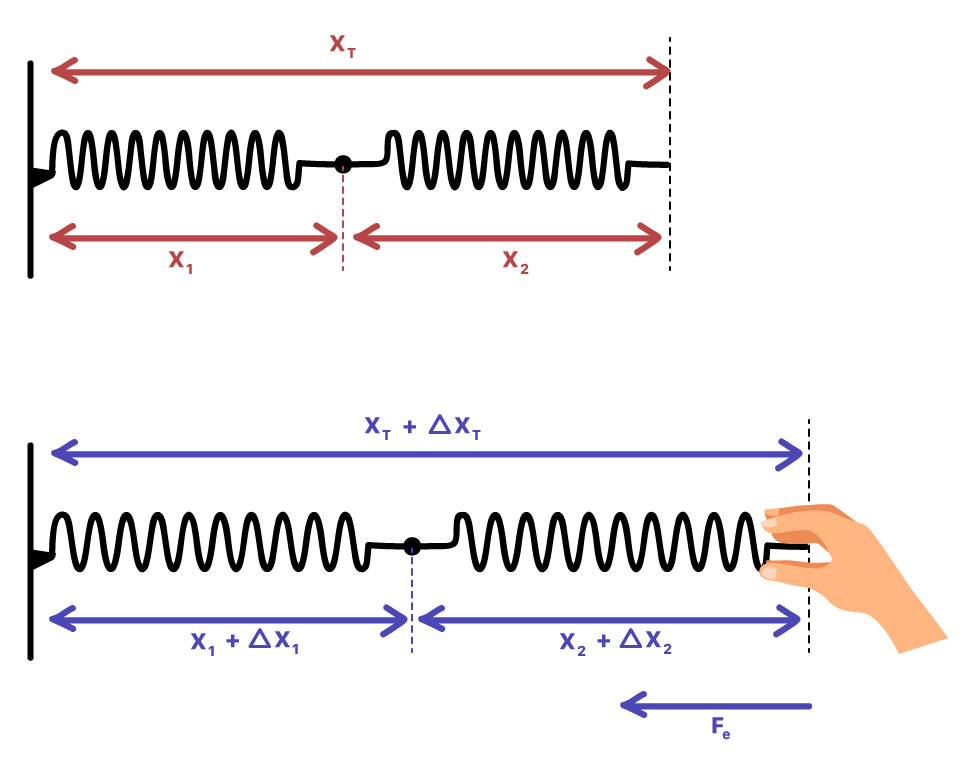
Ao puxar as molas, cada uma delas sofre uma deformação, representadas por Δx₁ e Δx₂. A soma de cada uma das deformações equivale à deformação total, que chamaremos de Δx_T. A força elástica é a mesma nas duas molas. Quando a primeira mola começa a deformar, ela exerce uma força elástica puxando a segunda, que reage tentando segurar a primeira. Essa disputa de forças faz com que ambas as molas exerçam a mesma força elástica. 

Unindo esses dois conhecimentos com a Lei de Hooke:

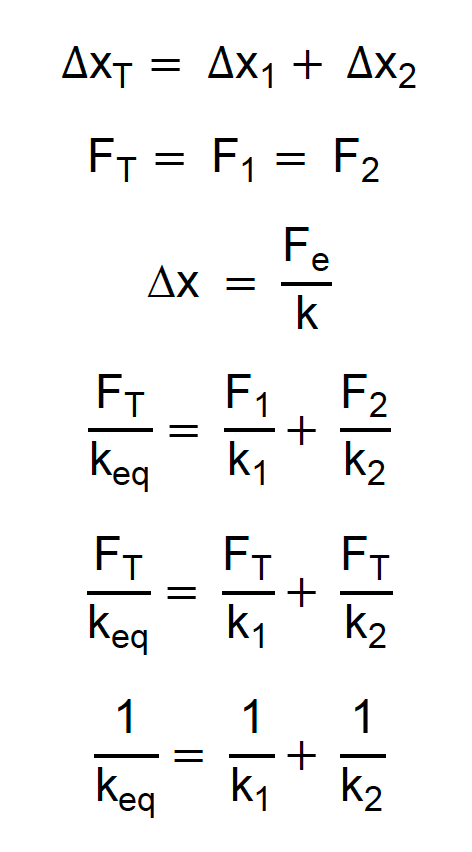
Perfeito! Quando associamos duas molas em série, a constante elástica equivalente depende da soma dos inversos das constantes elásticas. O que isso significa quando trabalhamos com valores? Por exemplo, se k₁ = 15 N/cm e k₂ = 10 N/cm, temos: 

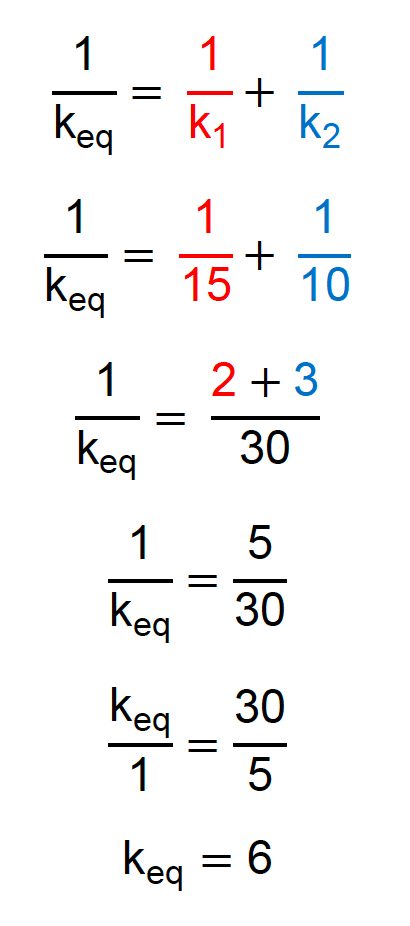
A constante elástica equivalente é 6 N/cm. Ou seja, quando colocamos uma mola de k₁ = 15 N/cm associada em série com outra de k₂ = 10 N/cm, a dureza dessa associação corresponde a uma mola de k_eq = 6 N/cm. E vai ser sempre assim, nas associações em série, a constante elástica equivalente será sempre menor do que todas as molas usadas.

Já que estamos falando de duas molas, podemos adaptar a fórmula para ter um resultado mais rápido dessa associação de molas:

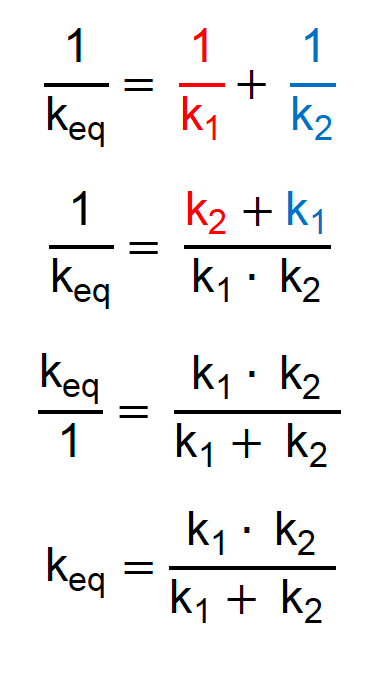
Essa relação especial pode ser usada nas associações de duas molas. Caso você tenha receio em lembrar dela, não tem problema, pois trata-se de apenas um desenvolvimento da fórmula geral.

 

2.1 Associação de uma quantidade qualquer de molas em série

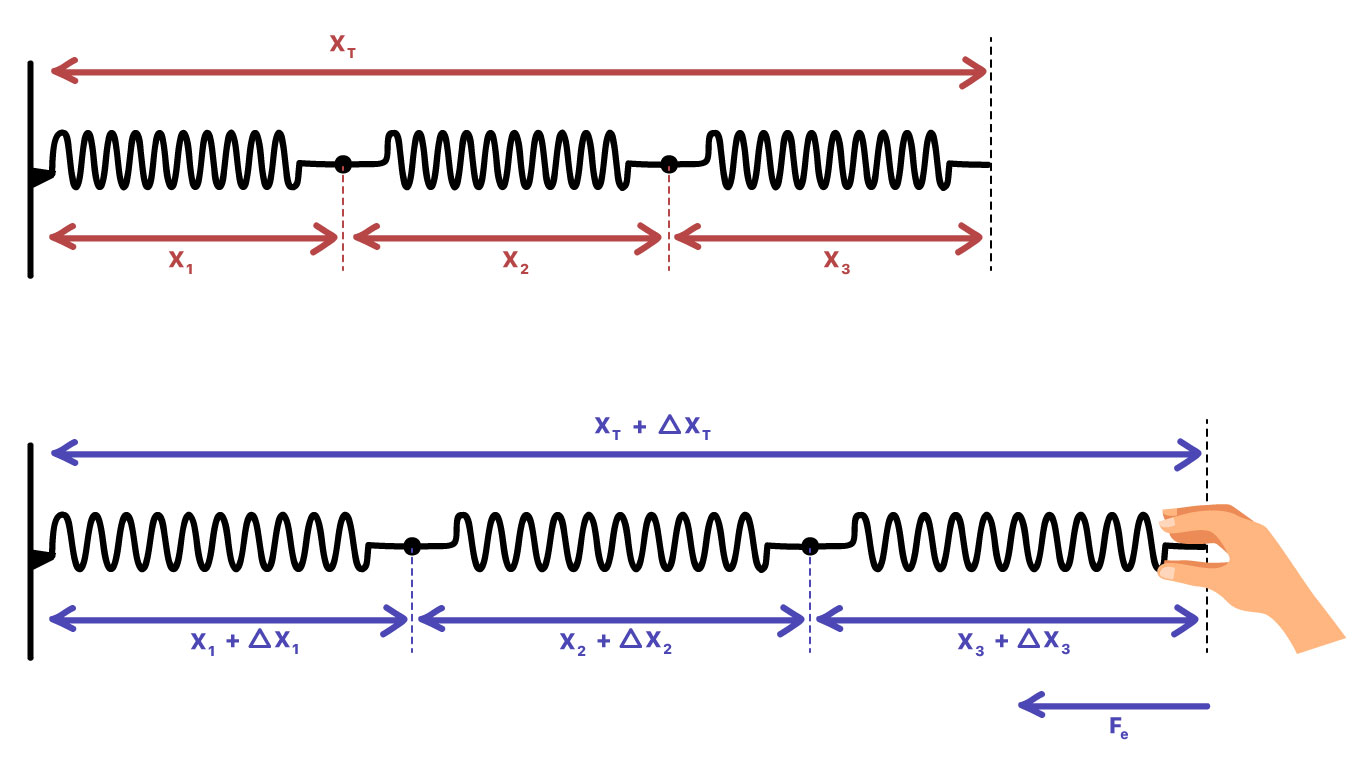
Já sabemos o que fazer quando associamos duas molas em série. Mas, e no caso de três? Ou quatro? E em cinco? Basta aplicar o mesmo raciocínio usado para as duas molas. Usaremos a imagem acima para mostrar como é ao associar três molas:

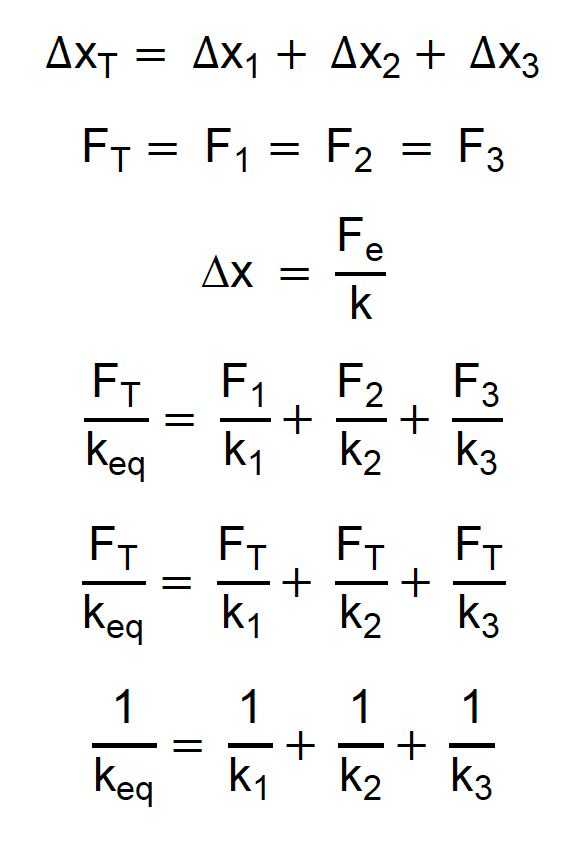
Como podemos notar, permanece a soma dos inversos. Assim, em quatro molas, teríamos:

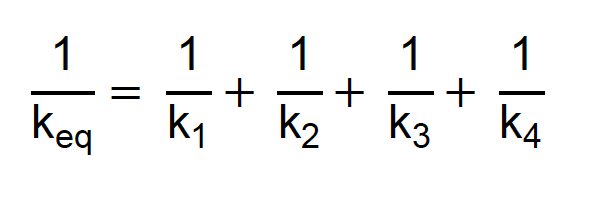
E assim por diante. Em uma associação de 10 molas em série, teremos a soma dos inversos das dez constantes elásticas. E lembrando, quanto mais molas colocarmos em série, menor será a dureza equivalente! 

Aqui, cabe relatar um caso especial: quando associamos molas iguais, basta dividir a constante elástica de uma delas pelo número de molas. 

Duas molas iguais:

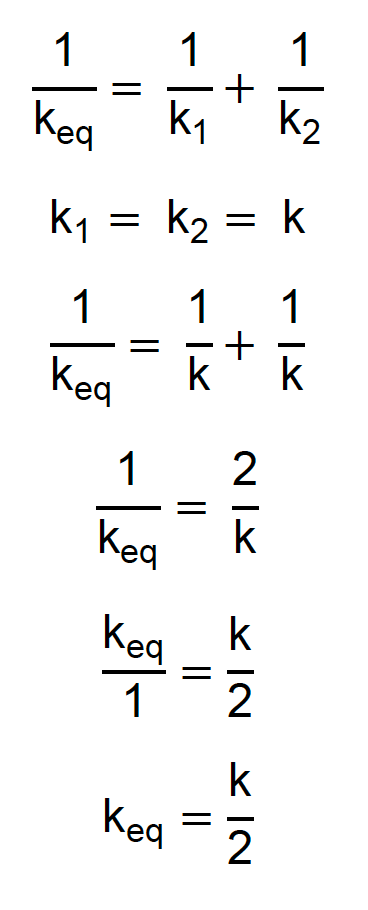
Aplicando a mesma lógica, no caso de três molas iguais:

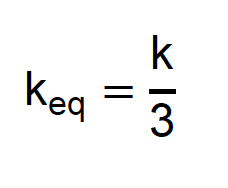
Para quatro molas iguais:

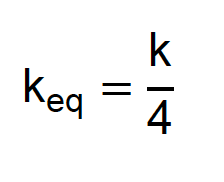
E assim segue. Então, quando associamos molas iguais, podemos usar essa divisão mais rápida, mas, a soma dos inversos funciona sempre. 

 

3. ASSOCIAÇÃO DE MOLAS EM PARALELO

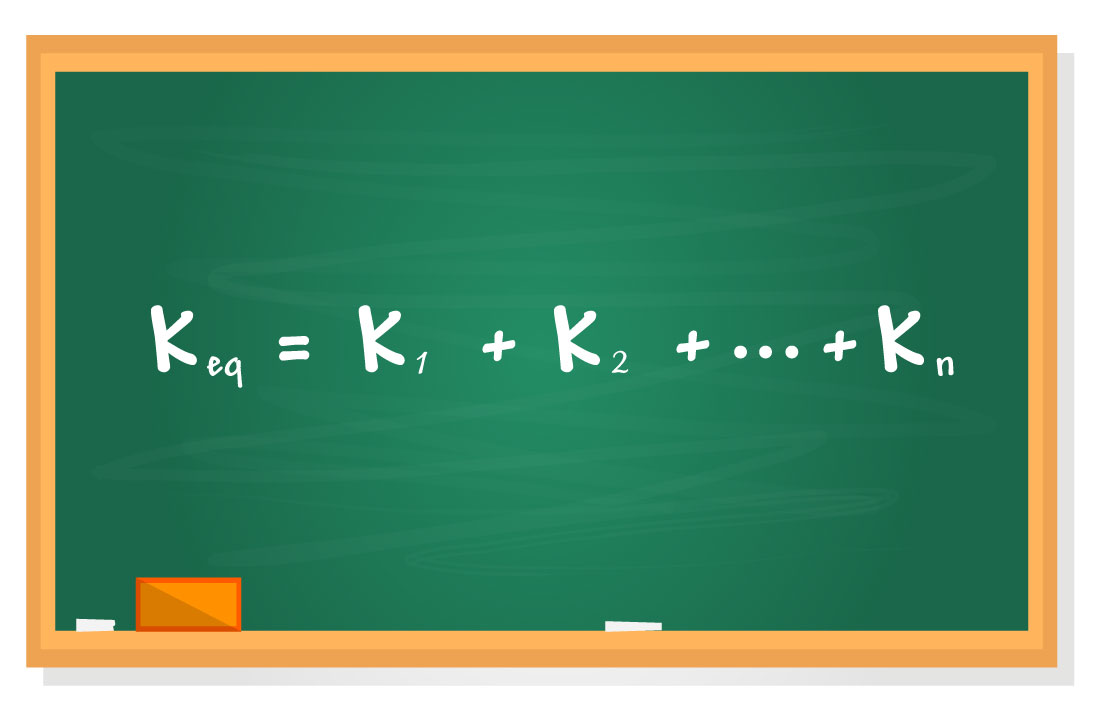
Já aprendemos como proceder ao trabalhar com as associações de molas em série. Mas, e quando elas estão em paralelo? Ou seja, quando colocamos molas lado a lado, como elas se comportam? Vejamos:

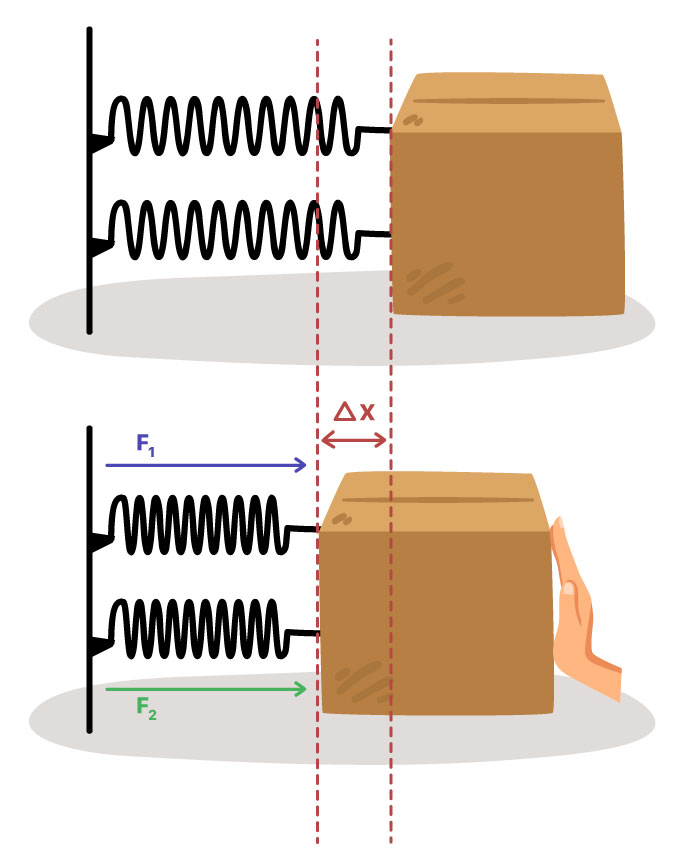
Associadas em paralelo, ambas as molas sofrem a mesma deformação. Nesse desenho, as duas molas estão comprimidas, as duas exercem força elástica empurrando o bloco para a direita. Assim, a força total exercida pelas molas é dada pela soma das forças individuais. Equacionando:

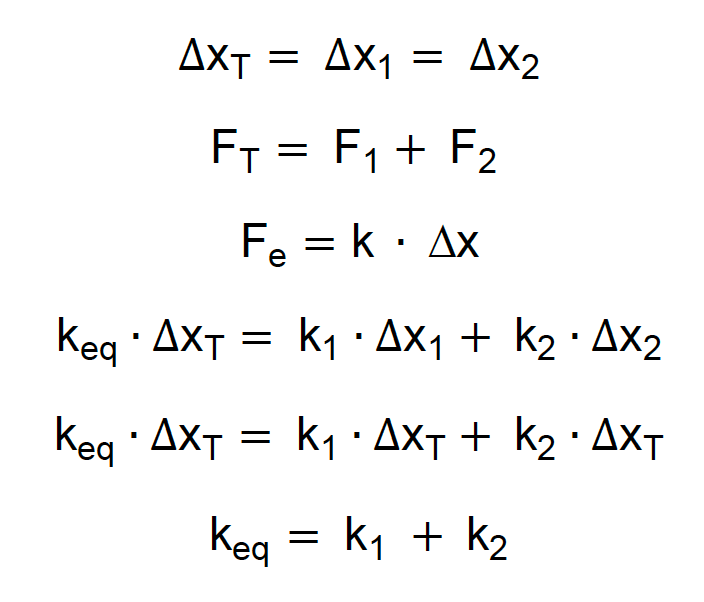
Perfeito, na associação de molas paralelas, a constante elástica equivalente é dada pela soma das constantes elásticas das molas associadas! Em outras palavras, somamos a dureza das molas. Um exemplo pode auxiliar nesse entendimento:

Considere duas molas, uma de k₁ = 15 N/cm e outra de k₂ = 10 N/cm, associadas em paralelo. Qual é a constante elástica equivalente?

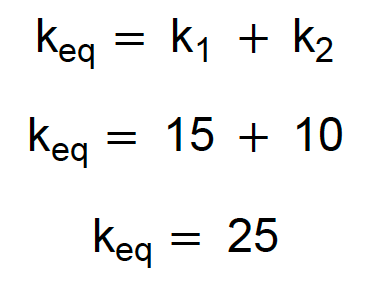
Você lembra do que vimos na associação em série dessas mesmas molas? Em série, elas equivalem a uma mola de k = 6 N/cm. Porém, em paralelo, lado a lado, equivalem a outra mola de k = 25 N/cm! 

 

3.1 Associação de uma quantidade qualquer de molas em paralelo

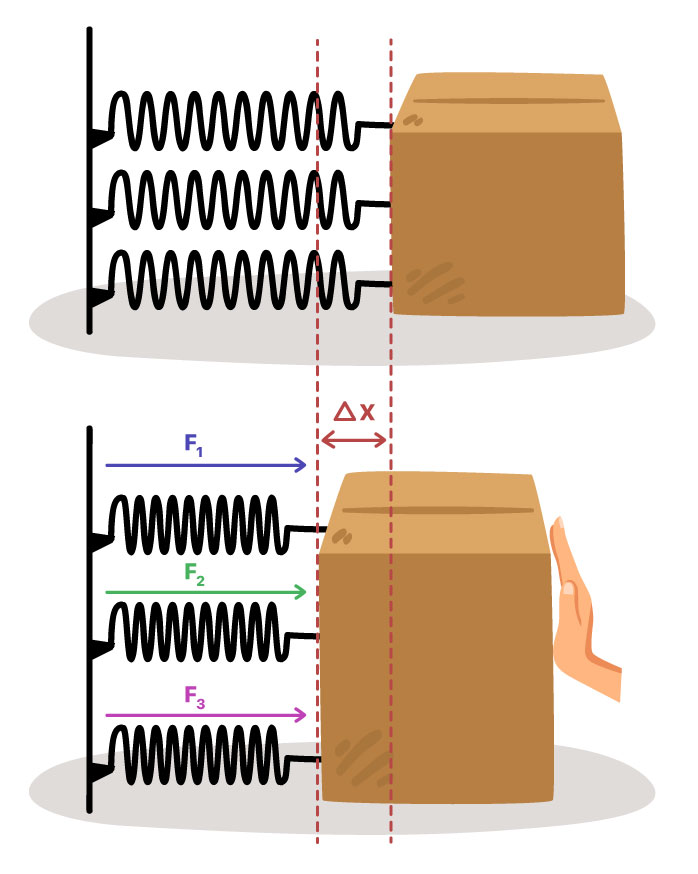
Agora, vejamos o que acontece ao associar três molas em paralelo. Na imagem acima, observamos a mesma lógica de quando associamos duas molas. Então, temos que:

Como consequência, temos o mesmo resultado: a constante elástica equivalente depende da soma das constantes de cada mola. Então, para quatro molas em paralelo, simplesmente teríamos:

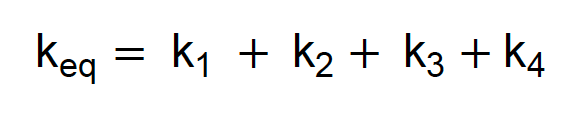
E assim vai.  Tal como vimos nas associações em série, também existe uma fórmula facilitada para quando molas iguais são postas em paralelo. Por exemplo, quando dez molas iguais são associadas em paralelo, basta somar a constante elástica de todas, ou seja, dez vezes a constante individual. 

Assim, para uma quantidade de molas iguais em paralelo, temos:

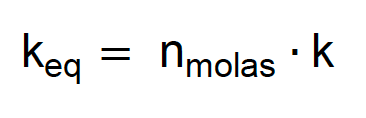
Até aqui, já aprendemos a calcular associações em série e em paralelo. Mas, e quando as associações forem mistas?

 

4. ASSOCIAÇÃO MISTA DE MOLAS

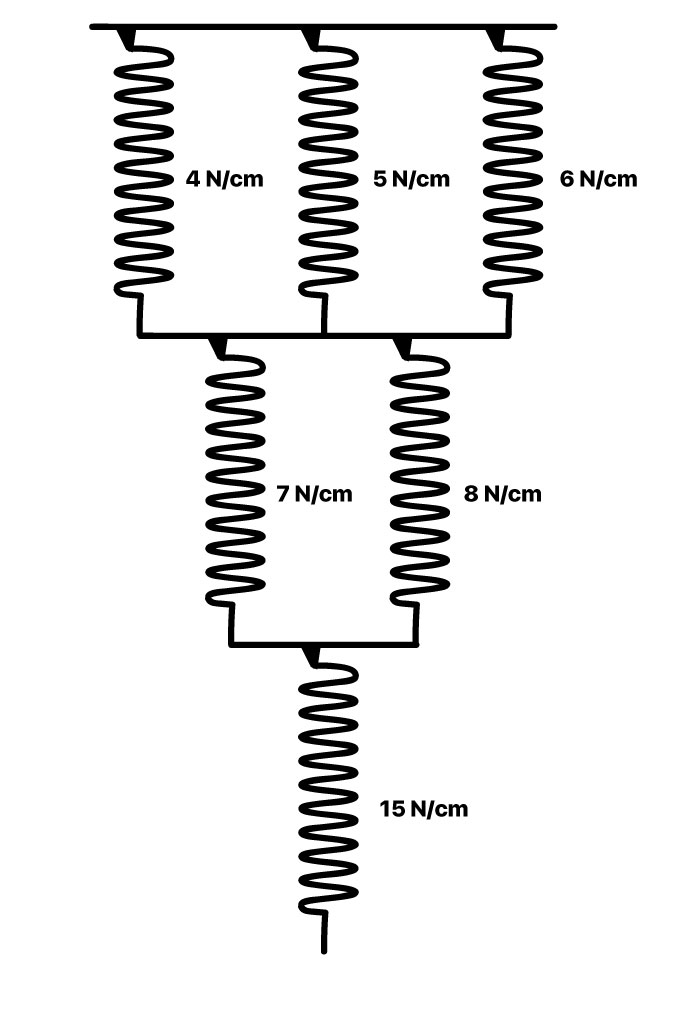
Como resolver a situação desenhada? Primeiramente, devemos identificar os menores agrupamentos de molas, que, nesse caso, são as molas paralelas. Existem dois grupos de molas em paralelo, vamos analisar cada um deles de modo individual.

Três molas em paralelo:

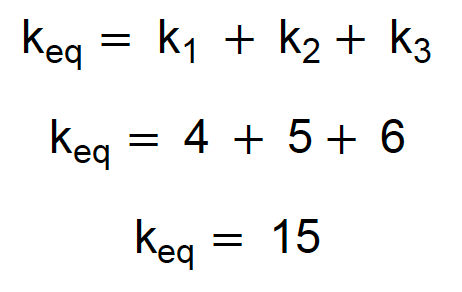
Duas molas em paralelo:

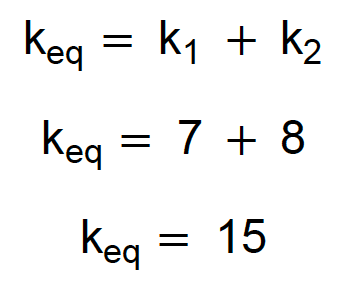
Perfeito, já resolvemos os grupos de associações em paralelo. Agora, podemos redesenhar a associação de molas de acordo com as constantes elásticas equivalentes:

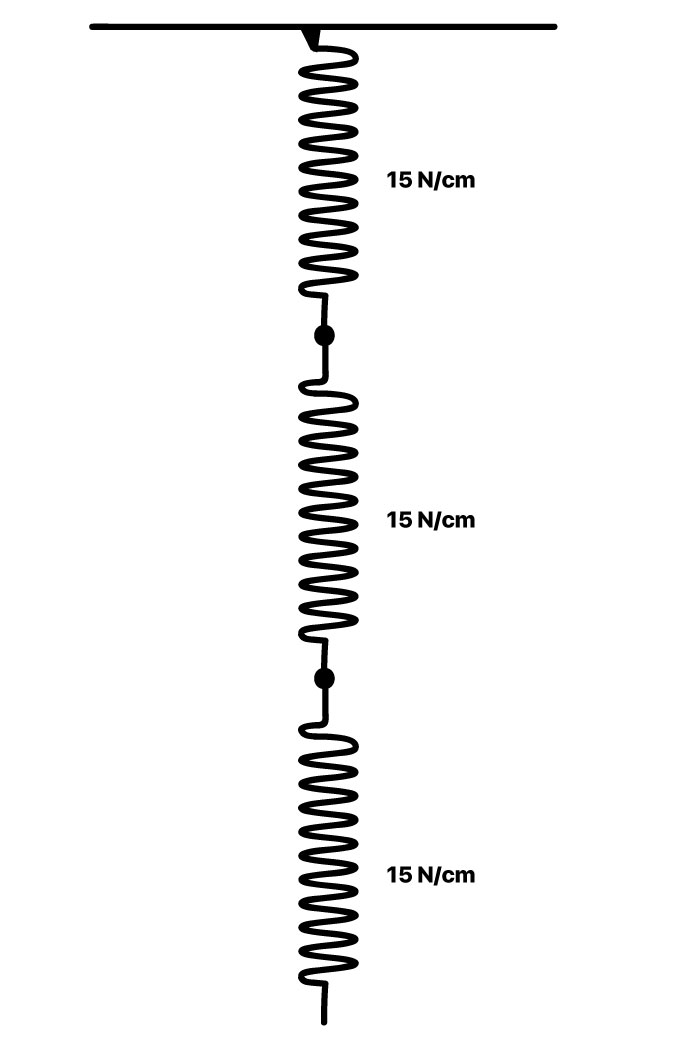
Agora, basta resolver essa associação em série. São três molas, todas iguais. Vou usar a fórmula especial para molas iguais em série e você pode usar a fórmula geral, para treinar:

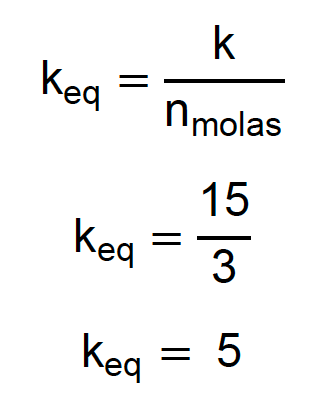
Perfeito, resolvemos assim essa associação de seis molas e encontramos uma constante equivalente de 5 N/cm. O segredo é resolver primeiro as partes menores. Nesse caso, as associações em paralelo eram as partes menores, então, resolvemos elas antes. Vejamos outro exemplo para fortalecer essa ideia:

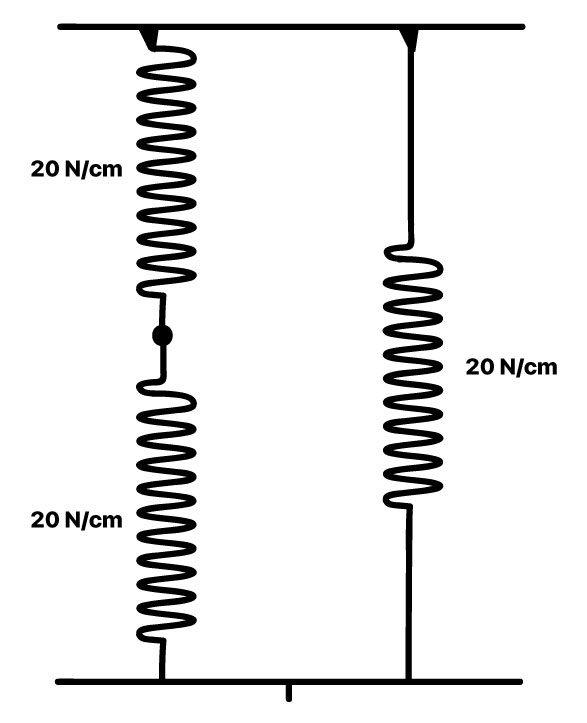
Aqui, resolveremos primeiro a associação em série:

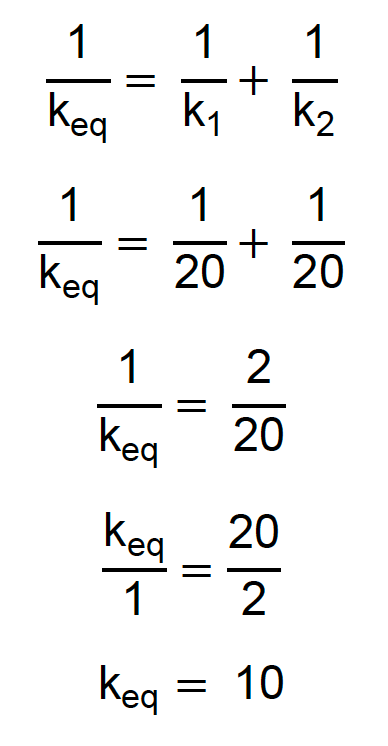
Agora, a situação correspondente:

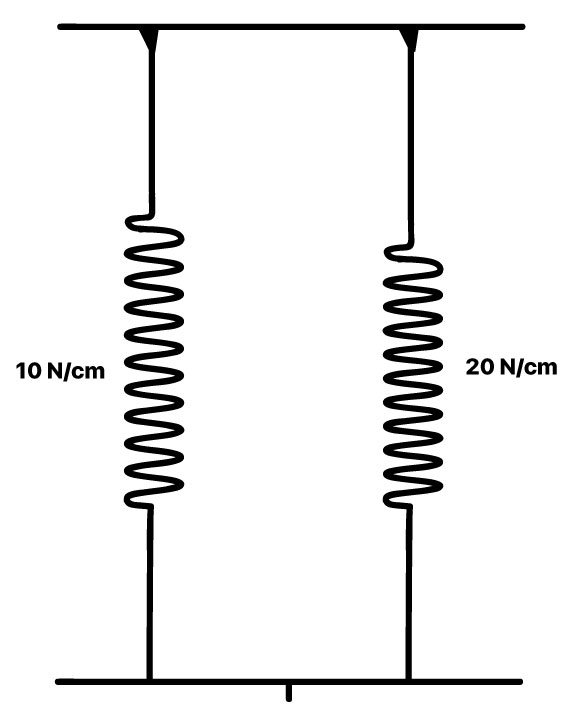
Finalmente, somamos as molas paralelas e temos nossa resposta:

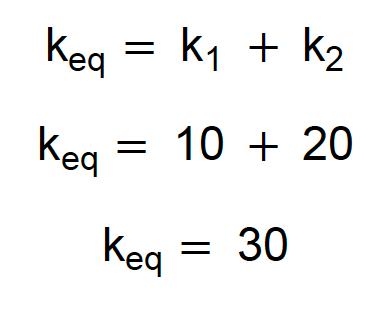
Pronto, a constante equivalente é 30 N/cm. Então, nas associações mistas de molas, devemos identificar os menores agrupamentos e começar a resolução por eles, aplicando o que já sabemos sobre molas em série e molas em paralelo.

 

Um breve resumo

Para finalizar, vamos elencar os pontos principais:

• Em uma associação de molas, buscamos trocar as molas por uma única de dureza equivalente.
• Ao associar molas em série, a dureza equivalente será sempre menor que a dureza de todas as molas usadas, obedecendo a soma de inversos.
• Ao associar molas em paralelo, a dureza equivalente será sempre maior que a dureza de todas as molas usadas, obedecendo uma soma normal.
• Em associações mistas, resolvemos primeiro as menores partes.

Certo, pessoal! Vimos que a associação de molas em série reduz a dureza equivalente, enquanto que a associação de molas em paralelo aumenta a dureza equivalente. Você consegue observar alguma associação de mola no seu dia-a-dia? Tente procurar e aplicar as noções aprendidas aqui para fortalecer o seu conhecimento! Uma dica: materiais dotados de elasticidade funcionam como molas.

Se você deseja continuar aprendendo, não deixe de conhecer a plataforma do Professor Ferretto! Para isso, basta clicar no botão abaixo:

 

A plataforma do Professor Ferretto oferece uma preparação completa para você arrasar em matemática e ciências da natureza nas provas do ENEM e dos vestibulares! Conheça os nossos planos e encontre o ideal para você:

Feito, pessoal? Um abração a todos e até o próximo post!