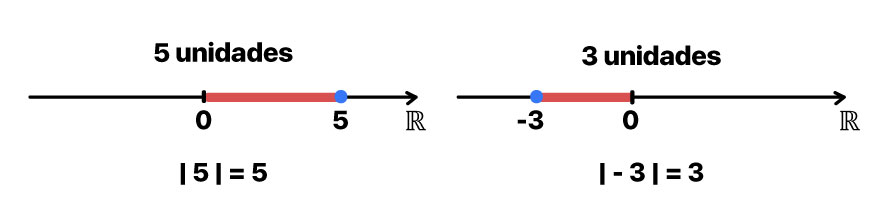
O módulo de um número real representa a distância deste número até a origem ou zero da reta real. Por representar geometricamente uma distância, o módulo de qualquer número real, seja ele positivo ou negativo, sempre resultará em um valor positivo.

 

Olá, pessoal! Tudo certo?

Hoje nós vamos estudar um assunto muito intrigante, que é base para o entendimento da função modular: o módulo de um número real. Depois de ler este texto vocês vão compreender, de uma vez por todas, a definição de módulo. Além disso, aprenderão a calcular o módulo de números e de expressões algébricas, algo muito importante para quem quer se dar bem nos vestibulares tradicionais e garantir uma vaga no ensino superior!

Vamos começar? Então, peguem seus materiais de estudo e sigam comigo!

 

1. O QUE É O MÓDULO OU O VALOR ABSOLUTO DE UM NÚMERO?

O módulo ou valor absoluto de um número real x, que representamos por |x|, é definido através da seguinte relação:

|x| = x, se x ≥ 0

|x| = – x, se x < 0

Isso significa que o módulo de um número real não negativo, ou seja, maior ou igual a zero, é igual ao próprio número. No entanto, o módulo de um número real negativo ou menor que zero é o valor oposto ao próprio número. Na prática, para obter o módulo de um número negativo, deve-se multiplicar esse número por “– 1”.

 

IMPORTANTE!

No início do texto, nós descobrimos que geometricamente, o módulo de um número real representa a distância desse número até a origem ou zero da reta real. Portanto, como não existem distâncias negativas, ao extrair o módulo de qualquer número real, sempre obtemos como resultado um número positivo.

Assim, caso seja necessário obter o módulo de um número positivo, fica claro, o resultado é o próprio número. Contudo, quando é preciso calcular o módulo de um número negativo, muitos alunos confundem o real significado da definição.

|x| = – x, se x < 0

Dizer que o módulo de x deve ser igual a –x quando x é menor que zero, não significa que o resultado desta operação é um valor negativo. Na verdade, isso mostra que o resultado é o valor oposto ao de x. Se x é um valor negativo, o valor oposto a ele, com toda a certeza, é um valor positivo. Para facilitar, tenham em mente que o valor numérico de x (quando x < 0) deve ser multiplicado por “– 1” a fim de se tornar um valor positivo.

Entendido, pessoal? Então, vamos aplicar essa ideia em alguns exemplos numéricos e algébricos. Vem comigo!

  

2. EXEMPLOS RESOLVIDOS SOBRE O MÓDULO DE UM NÚMERO REAL

Chegamos ao item mais importante deste texto, pessoal! Aqui, nós vamos aprender a aplicar as definições de módulo para números positivos e negativos. Vamos começar com exemplos que envolvem o módulo e as operações básicas da matemática. Acompanhem comigo!

 

2 ∙ |3|

Nesse caso, temos um produto entre um número natural e o módulo de um número positivo. Já que o módulo de um número positivo é igual ao próprio número, é possível resolver este produto facilmente.

2 ∙ |3| = 2 ∙ 3 = 6

 

|–4| + |–2|

Dessa vez, nos deparamos com uma adição entre dois módulos de números negativos. Sem problemas! Vamos aplicar a definição de módulo dos números negativos, e na sequência, realizar a soma dos resultados obtidos.

|–4| + |–2| = – (– 4) + [– (– 2)] = 4 + 2 = 6

Vejam que para resolver o cálculo apresentado, multiplicamos os valores negativos por “–1”. Mas é claro que quem já está dominando o assunto pode resolver tudo de forma mais direta. Basta pensar no seguinte: módulo de – 4 é 4, e módulo de – 2 é 2, e pronto!

 

|–7 + 2|

Nesse exemplo, nos deparamos com uma operação de soma dentro do módulo. Em situações como essa, devemos resolver primeiramente a operação, e depois aplicar a definição de módulo.  Olhem só!

|–7 + 2| = |–5| = – (– 5) = 5

Bem tranquilo, não é? Pois então, nos próximos itens, nós vamos resolver três exemplos que envolvem expressões algébricas. Em tais casos, é preciso analisar o comportamento da expressão de acordo com o valor numérico indicado para a incógnita. Conhecendo esse comportamento, é possível identificar qual definição de módulo deve ser aplicada: a dos números positivos, a dos números negativos, ou mesmo, as duas definições! Sigam comigo!

 

|5 – x| quando x = 8

Nessa situação, a incógnita x assume um valor definido. Assim, basta substituir esse valor na expressão, e obter o resultado da mesma forma que resolvemos o exemplo anterior.

|5 – x| = |5 – 8| = |–3| = – (– 3) = 3

 

|5 – x| com x > 5

Já nesse caso, a incógnita x pode assumir infinitos valores maiores do que 5. Por isso, para sabermos qual definição de módulo podemos aplicar a expressão, precisamos entender o que acontece quando valores maiores do que 5 substituem essa incógnita.

Para x = 6 → |5 – 6| = |–1|

Para x = 7 → |5 – 7| = |–2|

Para x = 8 → |5 – 8| = |–3|

Para x = 9 → |5 – 9| = |–4|

Para x = 10 → |5 – 10| = |–5|

Observem nos cálculos acima, que independentemente do valor maior que 5 escolhido para assumir o lugar de x, tem-se como resultado o módulo de um número negativo. Dessa forma, não há dúvidas de que devemos aplicar a definição de módulo de um número negativo a expressão “5 – x”.

|5 – x| = – (5 – x) = – 5 + x 

Portanto, o módulo de “5 – x” é igual a “– 5 + x” quando x > 5.

 

|5 – x| com x ∈ ℝ

Nesse exemplo, nossa situação se complicou um pouco, pessoal. Como vocês podem ver, precisamos definir o módulo da expressão “5 – x” quando x pode assumir qualquer valor real. Poderíamos pensar, primeiramente, em realizar alguns testes, vejam só!

Para x = –10 → |5 – (–10)| = |15|

Para x = 0 → |5 – 0| = |5|

Para x = 2 → |5 – 2| = |3|

Para x = 15 → |5 – 15| = |–10|

Reparem nos cálculos acima, que não existe um comportamento padrão para o módulo da expressão. Dependendo do número real aplicado, temos como resultado o módulo de um número positivo, ou o módulo de um número negativo. Para resolver esse caso, será necessário realizar o estudo do sinal da expressão. Vem comigo descobrir como fazer isso!

 

O estudo do sinal da expressão

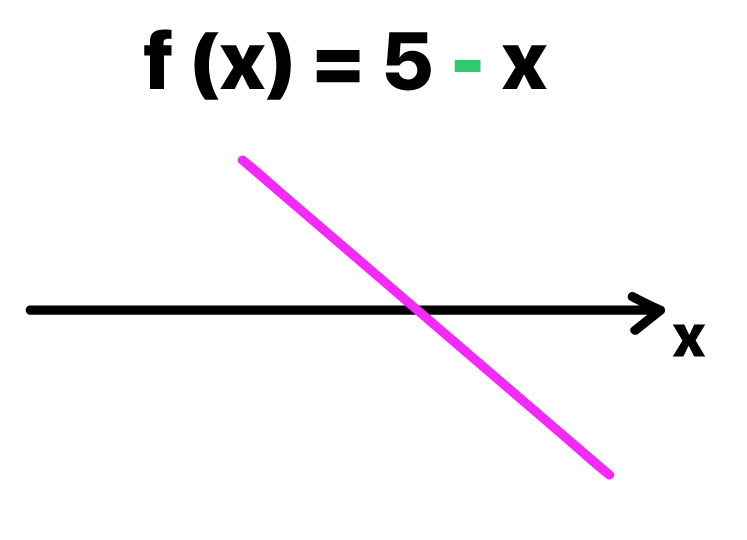
Para realizar o estudo do sinal da expressão “5 – x”, vamos considera-la uma função f(x). Dessa forma, como mostra a imagem acima, estamos diante da chamada função do 1º grau ou função afim.

A forma gráfica da função afim é uma reta, que pode ser crescente, quando o coeficiente angular da função é um valor positivo (a > 0), ou decrescente, quando o coeficiente angular da função é um valor negativo (a < 0). Por isso, a reta que representa a função f(x) = 5 – x é decrescente: o seu coeficiente angular é igual a “– 1”.

Dúvidas sobre o coeficiente angular da função afim? Então, clique aqui!

Agora, o próximo passo é identificar o ponto em que a reta da função f(x) = 5 – x intersecta o eixo x, ou seja, é preciso encontrar a raiz desta função. Para fazer isso, basta igualar a expressão a zero.

5 – x = 0

x = 5

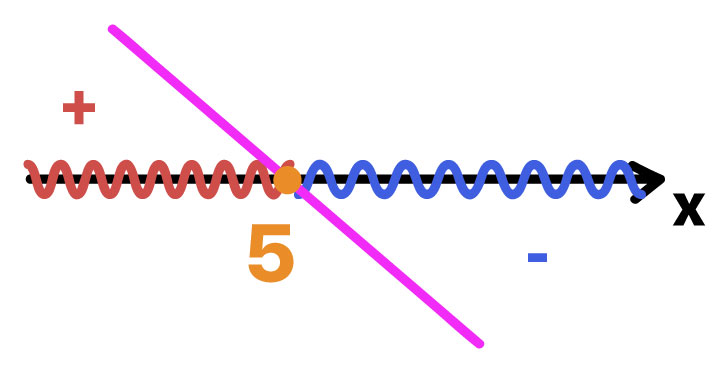
Sabendo que a reta que representa a função f(x) = 5 – x é decrescente, e que sua raiz é igual a 5, podemos tirar duas conclusões. A primeira delas é que para valores de x menores do que 5, a reta se encontra acima do eixo x, ou seja, para esses valores a função é positiva. A segunda conclusão é que para valores de x maiores do que 5, a reta se encontra abaixo do eixo x, ou seja, para esses valores, a função é negativa. Isso significa que para valores de x menores ou iguais a 5, o resultado da expressão será o módulo de um número não negativo, enquanto que para valores de x maiores do que 5, o resultado da expressão será o módulo de um número negativo. Vamos montar a sentença que representa essa situação.

 

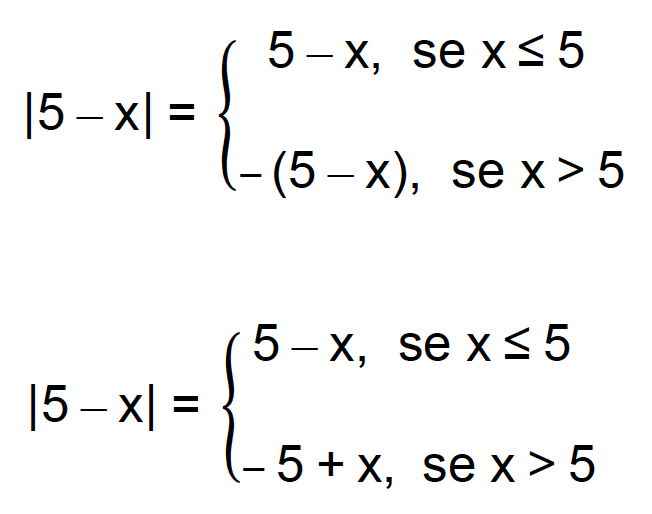
Encerrando com dicas especiais!

Conseguiram entender com clareza o resultado acima? Como foi necessário aplicar as duas definições de módulo na expressão em questão, o resultado teve de ser representado por uma sentença. Mas fiquem tranquilos, pessoal! No vídeo disponível logo abaixo eu explico este e outros exercícios ainda mais complexos sobre o assunto. Não deixem de conferir!

Gostou deste conteúdo? Clique aqui para saber como a Plataforma do Professor Ferretto funciona!

Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da Plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!

Um grande abraço, pessoal! Sucesso nos estudos!