
Os assuntos de Matemática que mais caem no ENEM vivem na sua cabeça, mas a nota não sai do lugar?...
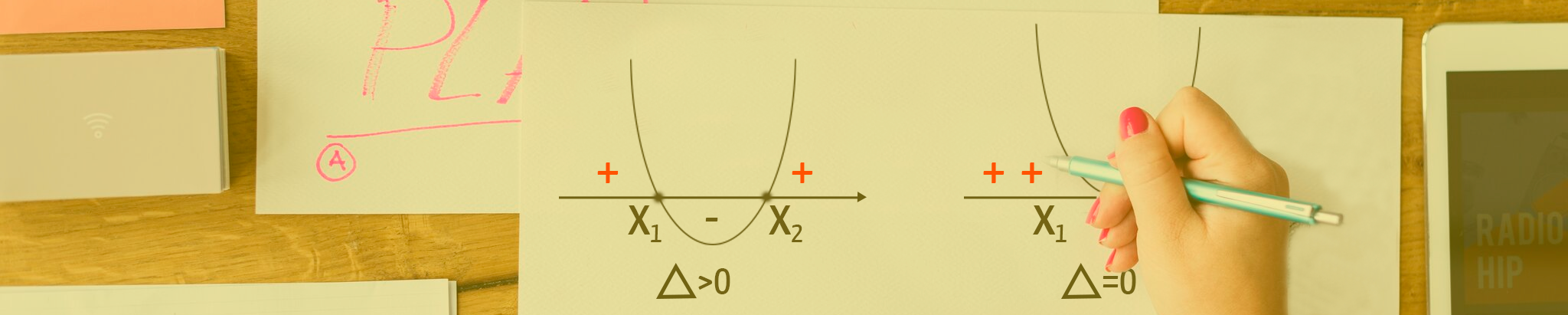
Realizar o estudo do sinal de uma função do 2º grau, significa determinar para quais valores de x a função é positiva, negativa ou igual a zero. Saiba tudo sobre o assunto aqui no texto!
Olá pessoal! Tudo tranquilo?
Quem está estudando bastante a matemática do ensino médio, seja com o intuito de prestar as provas do ENEM, dos vestibulares, ou mesmo para aprofundar o conhecimento no assunto, certamente está ciente do quanto é importante saber estudar o sinal de uma função, principalmente o da função do 2º grau, ou função quadrática, já que a sua forma gráfica é uma parábola. Por isso, no texto de hoje, eu vou mostrar para vocês como é simples fazer isso, desde que se conheça a natureza das raízes da função, e também a concavidade da parábola formada.
É verdade que o estudo do sinal de uma função do segundo grau, é base para o entendimento de outro conteúdo muito importante para a matemática de nível médio: as inequações do 2º grau. Mas se tudo que envolve a função quadrática não parece fazer sentido para vocês, ou caso a geometria, a análise combinatória, ou mesmo a probabilidade, estejam causando confusão, saibam que o Professor Ferretto pode lhes ajudar! Ele dispõe de uma plataforma de ensino 100% online, com videoaulas que abordam todos os assuntos da matemática do ensino médio. E olhem só que interessante: todas as questões das últimas provas do ENEM são resolvidas em vídeo por lá! Querem conhecer as demais vantagens da plataforma? Então acessem o site e saibam mais!
Depois dessa breve introdução, nada mais justo do que iniciarmos os nossos estudos, certo? Então vamos lá!
1. O QUE SIGNIFICA ESTUDAR O SINAL DE UMA FUNÇÃO DO 2º GRAU?
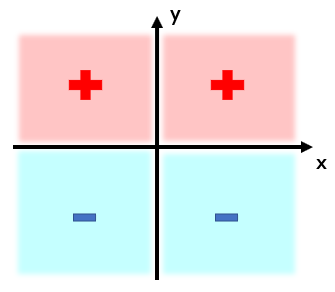
Estudar o sinal de uma função consiste em determinar os valores de x para os quais f(x) > 0, f(x) < 0, e f(x) = 0.
Bom, parece que estudar o sinal de uma função, significa determinar para quais valores de x ela é positiva (f(x) > 0), negativa (f(x) < 0), ou exatamente igual a zero (f(x) = 0). Para fazer essa determinação, nós iremos contar com a ajuda do gráfico da função do segundo grau em questão, a parábola, e por isso precisamos saber como ela pode nos mostrar todas essas informações. Nesse sentido, aí vai uma dica importante: a imagem acima é a primeira pista de onde deveremos prestar atenção!
Vejam pessoal, que o segredo é observar a localização do gráfico da função f(x) com relação ao eixo x, ou eixo das abscissas do plano cartesiano. Uma função é positiva, ou maior que zero (f(x) > 0), quando o seu gráfico se encontra acima do eixo x, da mesma forma que qualquer função é negativa, ou menor que zero (f(x) > 0), quando o seu gráfico se encontra abaixo do eixo x.

Pessoal, quando igualamos uma função a zero, não estamos justamente a procura de suas raízes? E as raízes de uma função, não são os pontos em que o gráfico corta, ou intersecta o eixo x? Pois então, uma função do 2º grau será igual a zero, quando os seus respectivos valores de x forem exatamente iguais as suas duas raízes! Graficamente, uma função do segundo grau será igual a zero nos pontos onde o gráfico corta ou intersecta o eixo x.
Pois bem, nós acabamos de ver que para realizar o estudo do sinal de uma função do 2º grau, é necessário obtermos as duas raízes dessa função, porque elas nos revelarão quando a função é igual a zero (f(x) = 0). Mas nós também vimos que é a forma gráfica da função em relação ao eixo x que nos ajuda a determinar quando a função é positiva e quando ela é negativa. Pessoal, é justamente aí que matamos dois coelhos com uma cajadada só: conhecer as raízes de uma função do 2º grau também nos permite desenhar facilmente a sua curva em relação ao eixo x!
Querem ver como isso acontece? A verdade é que dependendo da natureza das raízes da função, dada através do valor do discriminante, ou delta (Δ), cuja fórmula é apresentada logo abaixo, elas podem se comportar de 3 maneiras diferentes:
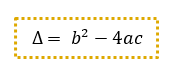
Do ponto de vista gráfico, podemos dizer que:
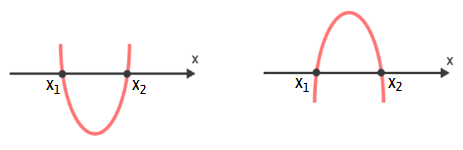
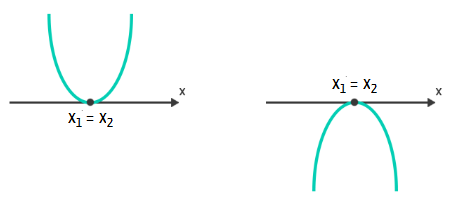
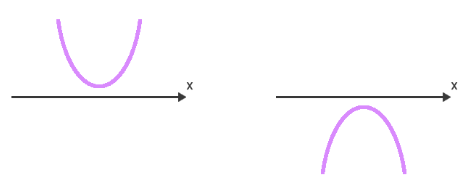
Agora, não podemos deixar de reparar em outro detalhe bem interessante: não é só a natureza das raízes da função que determina a forma gráfica da mesma. Em todos os 3 casos que acabamos de estudar, dois gráficos foram apresentados: em um deles, a parábola tem concavidade voltada para cima, enquanto no outro, ela tem concavidade voltada para baixo. A concavidade de uma parábola é determinada pelo coeficiente a, aquele que acompanha o termo x² na função do segundo grau. Se o valor numérico de a for positivo (a > 0), então a concavidade da parábola será voltada para cima, mas se o valor numérico de a for negativo (a < 0), então a concavidade da parábola será voltada para baixo.
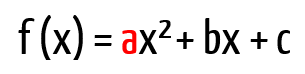
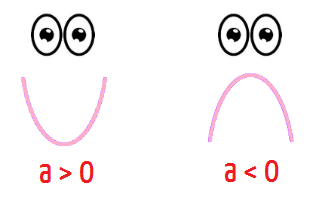
Tudo entendido? Neste momento, posso afirmar que vocês já têm todo o conhecimento necessário para efetuar o estudo do sinal de uma função quadrática, basta apenas organizarmos toda essa enxurrada de informações. Por isso, vamos estudar separadamente os 3 casos de estudo do sinal possíveis, tudo de acordo com as 3 formas que as raízes da função do 2º grau podem possuir. Vem comigo aqui!
1.1 Quando Δ > 0 e a função possui duas raízes reais e distintas
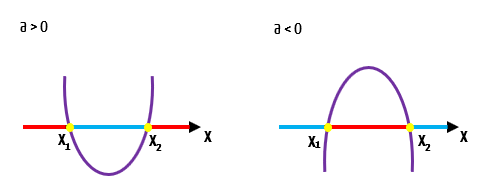
Nós já conhecemos a forma gráfica das funções do segundo grau que possuem duas raízes reais e distintas, não é mesmo? Por isso, a partir desse momento, vamos focar nossa atenção exclusivamente nos valores de x a cada ponto dos gráficos. Começaremos pelo caso em que a concavidade da parábola é voltada para cima (a > 0).
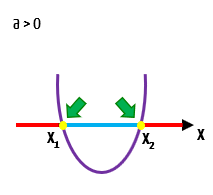
Não é segredo para nós, que quando x for exatamente igual a x1 ou exatamente igual a x2, a função f(x) será igual a zero, não é mesmo? É porque justamente nesses pontos, o gráfico corta, ou intersecta o eixo x. Agora, observem com atenção a imagem abaixo:
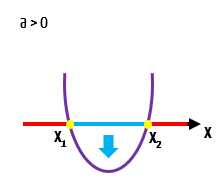
Para valores de x que se situam entre x1 e x2, reparem que o gráfico se encontra abaixo do eixo x. Isso significa que para valores de x entre x1 e x2, esta função é negativa!
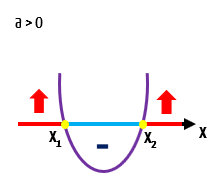
E o que dizer do gráfico da função quando os valores de x são menores do que x1 e maiores do que x2? Vejam na imagem acima, que ele se encontra acima do eixo x. Isso significa que para esses valores de x, a função é positiva!
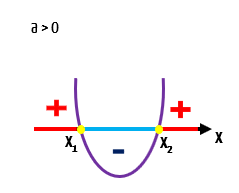
Pronto pessoal, acabamos de realizar o estudo do sinal para uma função f(x) que apresente essas características. Resta-nos agora, escrevermos direitinho todas as informações que obtemos:
f(x) = 0 ⟹ x = x1 ou x = x2
f(x) > 0 ⟹ x < x1 ou x > x2
f(x) < 0 ⟹ x1 < x < x2
E para o caso em que a concavidade da parábola é voltada para baixo (a < 0), muda alguma coisa? É claro que sim! Deem uma olhada na imagem abaixo:
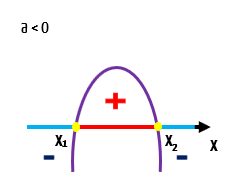
É claro que nesse caso, a função f(x) continua sendo igual a zero quando x for exatamente igual a x1, ou quando x for exatamente igual a x2. Mas ao invertermos a concavidade da parábola, para valores de x que se situam entre x1 e x2 a função acaba sendo positiva, pois seu gráfico se encontra acima do eixo x. Por outro lado, para valores de x menores que x1 e maiores que x2, a função acaba sendo negativa, já que seu gráfico se encontra abaixo do eixo x. Isso nos permite concluir que:
f(x) = 0 ⟹ x = x1 ou x = x2
f(x) > 0 ⟹ x1 < x < x2
f(x) < 0 ⟹ x < x1 ou x > x2
Bem fácil, não é mesmo? A ideia é a mesma para os próximos casos também, o que nos permitirá ser mais breves quanto aos seus estudos. Vamos continuar!
1.2 Quando Δ = 0 e a função possui duas raízes reais e iguais (raiz dupla)
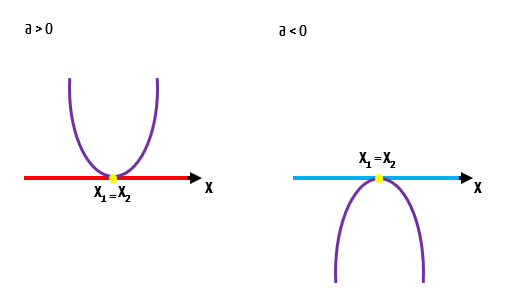
Curiosos esses casos não é mesmo? Novamente vamos começar por aquele onde a concavidade da parábola é voltada para cima (a > 0).
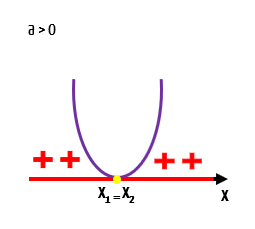
Como temos duas raízes reais e iguais nesse caso, é fato que existe um único valor de x para o qual a função f(x) é igual a zero, x1, que é o mesmo valor de x2. Agora, o detalhe mais interessante, é que para qualquer outro valor real de x a função é positiva, porque o seu gráfico está localizado acima do eixo x. Isso significa que não existe nenhum valor de x que torne a função negativa, e que qualquer valor de x diferente do valor das raízes, torna a função positiva.
f(x) = 0 ⟹ x = x1 = x2
f(x) > 0 ⟹ x ≠ x1 ou x ≠ x2
É claro que uma mudança na concavidade gera diferenças no estudo do sinal da função. Novamente, como temos duas raízes reais e iguais, existe um único valor de x para o qual a função f(x) é igual a zero, x1, que é o mesmo valor de x2. Só que nesse caso, para qualquer outro valor real de x a função é negativa, porque o seu gráfico está localizado abaixo do eixo x. Isso significa que não existe nenhum valor de x que torne a função positiva, e que qualquer valor de x diferente do valor das raízes, torna a função negativa.
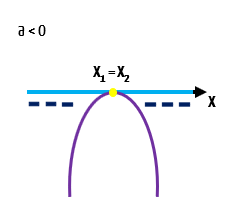
f(x) = 0 ⟹ x = x1 = x2
f(x) < 0 ⟹ x ≠ x1 ou x ≠ x2
1.3 Quando Δ < 0 e a função possui duas raízes complexas
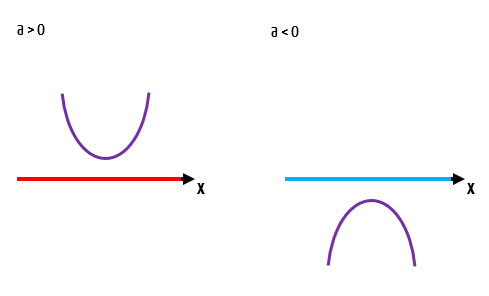
Esse é o caso mais simples de estudo do sinal de uma função quadrática. Isso acontece porque as raízes não pertencem ao conjunto dos números reais, e portanto, não precisamos nem mesmo encontrar os seus valores numéricos. Basta fazermos um esboço da representação gráfica da função, tudo de acordo com a concavidade da sua parábola.
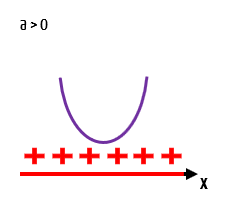
Observem na figura acima, que o fato de não existirem raízes reais para a função, faz com que seu gráfico nem mesmo encoste no eixo x. Isso nos mostra que não existem valores reais de x para os quais a função f(x) seja igual a zero, e nem mesmo valores de x que tornem a função negativa, já que toda a parábola está localizada acima do eixo x. Assim, para qualquer valor real de x, uma função como essa será sempre positiva!
f(x) > 0 ⟹ x ∈ ℝ
Quando a concavidade da parábola é invertida, é claro que as coisas mudam de figura. Na imagem abaixo, é possível ver que o gráfico sequer encosta no eixo x. Isso nos mostra que não existem valores reais de x para os quais a função f(x) seja igual a zero, e nem mesmo valores de x que tornem a função positiva, já que toda a parábola está localizada abaixo do eixo x. Assim, para qualquer valor real de x, uma função como essa será sempre negativa!
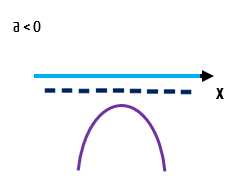
f(x) < 0 ⟹ x ∈ ℝ
Feito pessoal? Qualquer função do segundo grau existente sempre se enquadrará em algum desses casos que acabaram de ser apresentados, sem exceções. Por isso, ler esse texto com atenção, e revisar todo conteúdo através do vídeo que se encontra logo abaixo, é a receita do sucesso para que não restem mais dúvidas quanto ao estudo do sinal de uma função quadrática!
Ainda é importante ressaltar, que neste texto nós falamos muito das raízes de uma função do 2º grau, mas não falamos especificamente de como é possível encontrar os seus valores numéricos. Pessoal, seja qual for o conteúdo em que as raízes de uma função quadrática estejam envolvidas, é fato que vocês sempre poderão encontra-las através da fórmula de Bhaskara ou do método da soma e produto, como nós já vimos aqui no blog.
E por fim, caso a dúvida de vocês não tenha nada a ver com as funções do segundo grau, mas sim com os sinais de desigualdade (> e <), aqui vai uma última dica importante: o texto Introdução à inequação do 1º grau, que nós também já vimos aqui no blog, fala tudo sobre eles!
Bom, como sempre, uma hora o texto chega ao fim, ainda bem! Por isso, eu fico por aqui! Um forte abraço a todos e até mais!
