APLICANDO O ESTUDO DO SINAL DE UMA FUNÇÃO DO 2º GRAU

Olá pessoal! Tudo bem com vocês?

Nós já estudamos aqui no blog como é possível realizar o estudo do sinal da função quadrática, função esta, que também é muito conhecida como função polinomial do 2º grau. Mas o fato é que nós ainda não aplicamos todos os conceitos que vimos, ou seja, não resolvemos nenhum exercício sobre o assunto. Como tudo na vida, um aprendizado só ganha sentido quando podemos utilizá-lo na prática, e por isso, o nosso texto de hoje será focado exclusivamente em um roteiro prático para resolução de questões que envolvam o estudo do sinal de uma função do 2º grau.

Assim, se vocês são estudantes do ensino médio, e/ou estão buscando uma vaga no ensino superior através das provas do ENEM e dos vestibulares, já aviso de antemão: não dá para perder o texto de hoje! Mas eu se você fosse vocês, também não perderia a oportunidade de conhecer o curso de matemática 100% online do Professor Ferretto! Só na plataforma do Ferretto, vocês encontram videoaulas sobre todo o conteúdo de matemática do ensino médio, e mais de 1000 exercícios do ENEM e de vestibulares disponíveis para resolução! Isso que eu nem falei sobre os simulados semanais, os planos de estudo disponíveis e sobre as aulas de física! Acessem o site para descobrir todas as vantagens do curso e como ter acesso a ele!

E agora, para fecharmos com chave de ouro essa introdução, lá vem o Ferretto com uma daquelas dicas que não dá para perder. Pessoal, se vocês ainda não acompanharam o texto Estudo do sinal de uma função quadrática, saibam que é muito importante fazer isso antes de continuar esta leitura! Lá vocês encontram a teoria detalhada deste assunto, e para o sucesso de vocês, teoria e prática devem andar juntas!

Estudar o sinal de uma função consiste em determinar os valores de x para os quais f(x) > 0, f(x) < 0, e f(x) = 0.

Bom, foi dito logo acima, que faríamos um roteiro prático para determinar os valores de x que tornam uma certa função do segundo grau positiva (f(x) > 0), negativa (f(x) < 0), ou exatamente igual a zero (f(x) = 0). Isso significa que a promessa era descrever todos os passos necessários para realizar o estudo do sinal de uma função do 2º grau. Pois bem, sem mais delongas, aí vão eles:

 

1º Passo: observar a função do 2º grau e extrair dela o valor numérico dos coeficientes a, b, e c.

 

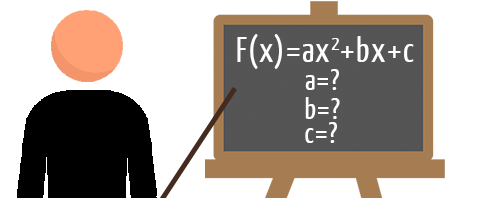
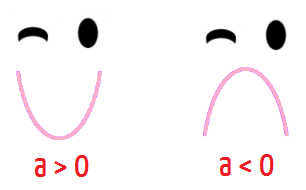
Ao extrair os coeficientes da função do segundo grau, já aproveitem para reparar melhor no valor numérico do coeficiente a: se ele for positivo, a concavidade da parábola formada será voltada para cima, mas se ele for negativo, a concavidade da parábola formada será voltada para baixo.

 

2º Passo: calcular o valor do delta (Δ), ou do discriminante da função do 2º grau, para determinar a natureza das duas raízes dessa função.

 

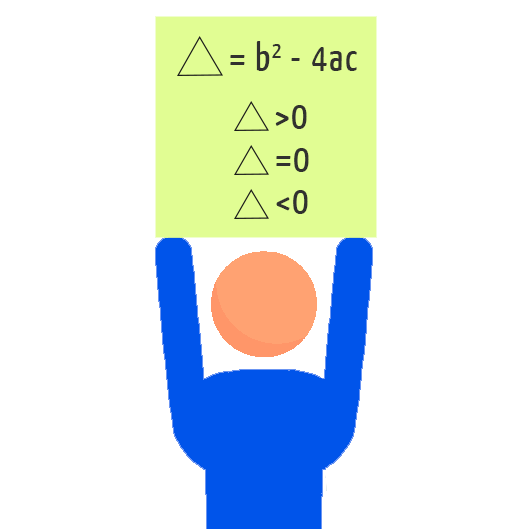
O valor do discriminante da função do segundo grau é tão importante, porque determina qual é o número de pontos em que a parábola intersecta, ou corta, o eixo x do plano cartesiano. Acompanhem nos itens abaixo como isso se dá:

• Se Δ > 0, ou seja, um valor positivo, então as duas raízes da função serão reais e distintas (x₁ ≠ x₂), e a parábola vai cortar o eixo x em dois pontos distintos;

• Se Δ = 0, então as duas raízes serão reais e iguais (x₁ = x₂), e a parábola irá tocar o eixo x em um único ponto;

• Se Δ < 0, ou seja, um valor negativo, então as duas raízes serão imaginárias, e a parábola não irá sequer encostar no eixo x, estando totalmente acima, ou totalmente abaixo dele.

 

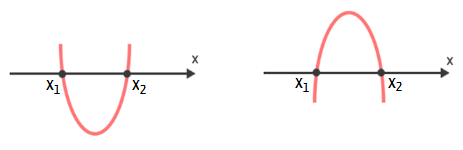
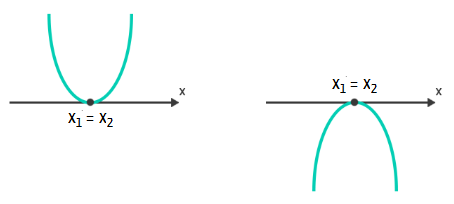
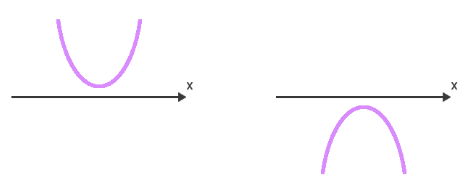
3º Passo: se a função do 2º grau possuir raízes reais (Δ > 0 ou Δ = 0), calcular o valor numérico dessas raízes.

 

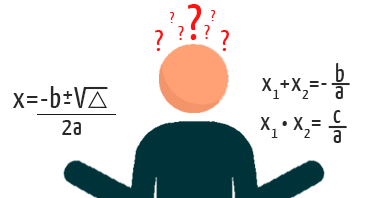
Nós já estudamos aqui no blog, que as raízes de uma função do segundo grau podem ser obtidas através da famosa fórmula de Bhaskara, ou então através do método da soma e produto. Assim, vocês têm duas opções para executar esse passo: escolham o método de sua preferência!

 

4º Passo: realizar o esboço do gráfico da função, e concluir o seu estudo do sinal.

 

Vocês viram como estudamos o sinal de cada um dos 3 casos existentes no texto Estudo do sinal de uma função quadrática, não é mesmo? Então chega de conversa! Vamos aplicar esses 4 passos em alguns exercícios. Vem comigo aqui!

 

Estudar o sinal das seguintes funções:

a. f(x) = x² – 3x – 4

a = 1

b = – 3

c = – 4

Vejam, o valor numérico de a é positivo! Isso nos permite concluir que a concavidade da parábola de f(x) será voltada para cima!

Δ = b² – 4ac

Δ = (– 3)² – 4 ∙ 1 ∙ (– 4)

Δ = 9 + 16

Δ = 25 → Δ > 0

Ora, e não é que teremos duas raízes reais e distintas (Δ > 0)! Assim, só nos resta encontrar seus valores numéricos, e para isso, faremos uso do método da soma e produto.

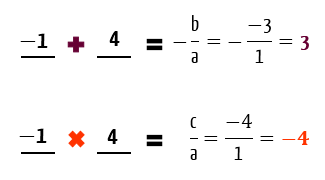
Quando os valores –1 e 4 são somados, eles resultam no valor 3. Ao mesmo tempo, quando ambos os valores são multiplicados, eles resultam em –4.  Pronto! Nada mais é preciso para afirmar que as raízes de f(x) são x₁ = –1, e x₂ = 4. Agora já temos informações suficientes para esboçar o gráfico de f(x) e estudar o seu sinal.

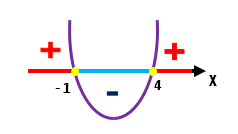
Observem que para valores de x menores do que –1, e maiores do que 4, a função f(x) é positiva. Já para valores de x que se situam entre –1 e 4, a função f(x) é negativa. E por fim, mas não menos importante, a função f(x) é igual a zero quando x é exatamente igual a –1, ou exatamente igual a 4.

f(x) = 0 ⟹ x = – 1  ou x = 4

f(x) > 0 ⟹ x < – 1 ou x > 4

f(x) < 0 ⟹ – 1  < x < 4

Entendido, pessoal? Não tem mistério, não é mesmo? Então vamos aos próximos exercícios, que resolveremos de uma forma um pouquinho mais breve.

 

b. f(x) = – 3x² + 2x + 1

a = – 3

b = 2

c = 1

Nesse caso, o valor numérico de a é negativo, o que significa que a concavidade da parábola de f(x) será voltada para baixo!

Δ = b² – 4ac

Δ = 2² – 4 ∙ (– 3) ∙ 1  

Δ = 4 + 12

Δ = 16 → Δ > 0

Novamente teremos duas raízes reais e distintas (Δ > 0), mas dessa vez nós vamos obter os seus valores numéricos através da fórmula de Bhaskara. Acompanhem com atenção!

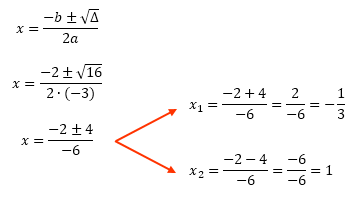
De posse das raízes de f(x), que são x₁ = –1/3  e x₂ = 1, já temos condições de esboçar o gráfico da função e estudar o seu sinal.

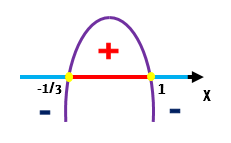
Observem que para valores de x menores do que –1/3, e maiores do que 1, a função f(x) é negativa. Já para valores de x que se situam entre –1/3 e 1, a função f(x) é positiva. E por fim, a função f(x) só pode ser igual a zero quando x for exatamente igual a –1/3 ou exatamente igual a 1.

f(x) = 0 ⟹ x = – 1/3  ou x = 1

f(x) < 0 ⟹ x < – 1/3 ou x > 1

f(x) > 0 ⟹ – 1/3  < x < 1

 

c. f(x) = x² + 4x + 4

a = 1

b = 4

c = 4

Vejam que neste item, o valor numérico de a é positivo, o que significa que a concavidade da parábola de f(x) será voltada para cima!

Δ = b² – 4ac

Δ = 4² – 4 ∙ 1 ∙ 4  

Δ = 16 – 16

Δ = 0

Olhem só, e não é que encontramos um delta de valor zero? É claro que isso não é um problema, pois esse dado nos mostra apenas que a função possui duas raízes reais e iguais. De qualquer forma, nós precisamos obter os valores numéricos dessas raízes, e é isso que faremos agora através da fórmula de Bhaskara. Fiquem atentos!

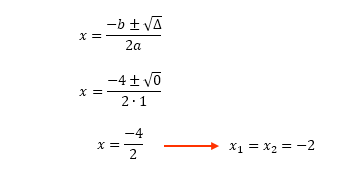
Vocês já conhecem a forma gráfica de uma função quadrática que possui duas raízes reais e iguais, não é mesmo? Então vamos logo construir esse gráfico para estudarmos o sinal da função f(x).

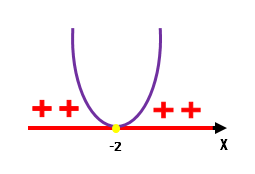
Reparem que nesse caso, para todo e qualquer valor real de x diferente de –2, a função f(x) é positiva. Já se x for exatamente igual a –2, então a função f(x) será exatamente igual a zero. Mas o mais curioso de tudo, é que o fato de a parábola não possuir parte alguma abaixo do eixo x, nos permite concluir que não existem valores reais de x que possam tornar a função negativa!

f(x) = 0 ⟹ x = –2

f(x) > 0 ⟹ x ≠ –2

 

d. f(x) = x² + 2x + 8

a = 1

b = 2

c = 8

Observem que o valor numérico de a é positivo, o que significa que a concavidade da parábola de f(x) será voltada para cima!

Δ = b² – 4ac

Δ = 2² – 4 ∙ 1 ∙ 8  

Δ = 4 – 32

Δ = –28 → Δ < 0

Ops! O delta é valor menor que zero! Mas podem acreditar que para o estudo do sinal da função quadrática, isso é motivo de comemoração! Quando o delta resulta em um valor negativo, ele indica que a função do 2º grau não possui raízes reais (x₁ e x₂ ∉ ℝ), o que nos permite pular o passo do cálculo das raízes, e partir direto para a o esboço do gráfico.

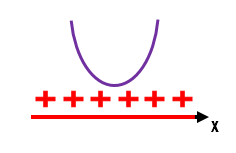
O esboço acima não deixa dúvidas de que para qualquer valor real de x, essa função f(x) será sempre positiva. Isso porque a parábola está totalmente localizada na parte superior do eixo x, e nem sequer encosta nesse eixo. Assim, não há nenhum valor de x que possa tornar a função negativa, ou mesmo igual a zero.

f(x) > 0 ⟹ x ∈ ℝ

Gostaram do texto, pessoal? Aplicar a teoria a alguns exercícios torna tudo mais dinâmico, não é mesmo? Por isso, espero que todo o conhecimento visto aqui tenha sido proveitoso para os estudos de vocês, e que possa lhes ajudar a dominar outros conteúdos, como por exemplo, aqueles que tem relação com a função do segundo grau, ou mesmo com o estudo do sinal de qualquer outra função matemática. O vídeo que está em anexo, nada mais é do que um complemento do que vocês acabaram de ler, e como sempre, possui mais alguns exercícios resolvidos que são muito valiosos. Não custa nada dar uma olhadinha nele, certo?

E eu vou ficando por aqui! Espero vocês no próximo texto! Um abração!