POTÊNCIA DE PONTO EM RELAÇÃO A CIRCUNFERÊNCIA

Olá pessoal! Como vão vocês?

Estudar a potência de um ponto em relação a uma circunferência é muito importante para a geometria plana, principalmente porque esse conceito permite definir algumas relações métricas entre retas tangentes e secantes a circunferência. É por isso que estamos aqui hoje! Vamos descobrir como relacionar o comprimento de duas cordas que se interceptam em um ponto interno a circunferência, e também estudaremos a relação entre os comprimentos de retas secantes e tangentes que se interceptam em um ponto externo a uma determinada circunferência. Depois de aprender os super macetes do Ferretto que envolvem o assunto, acreditem, vocês serão imbatíveis nas provas de matemática dos vestibulares que estão por vir!

Mas antes de iniciarmos os estudos, aí vai uma dica muito valiosa para quem é estudante do ensino médio e pretende realizar as provas do ENEM e dos vestibulares mais tradicionais do país: para compreender e aplicar a matemática com facilidade, não existe nada melhor do que entender o conceito do assunto de verdade, sem decorar fórmulas e exercícios. É por isso que o Professor Ferretto sempre tem uma dica de interpretação ou um macete interessante para ensinar em cada conteúdo da matemática do ensino médio. E o melhor de tudo, é que todo esse conhecimento está bem pertinho de vocês, em uma plataforma de ensino 100% on-line! Querem saber como ter acesso aos simulados, aos exercícios resolvidos em vídeo, a monitoria, aos planos de estudos, as aulas de física, e a tudo que está disponível por lá? Então acessem o site, e descubram como é fácil ser aluno do Professor Ferretto!

Bom, já que vocês estão ansiosos para começar, vou resumir brevemente o que vem por aí. O primeiro caso que abordaremos, será aquele em que duas cordas se intersectam em um ponto interior a circunferência. Na sequência, falaremos sobre os dois possíveis casos em que retas secantes e tangentes se intersectam em pontos externos a circunferência. Vem comigo aqui!

 

1º CASO: PONTO INTERIOR

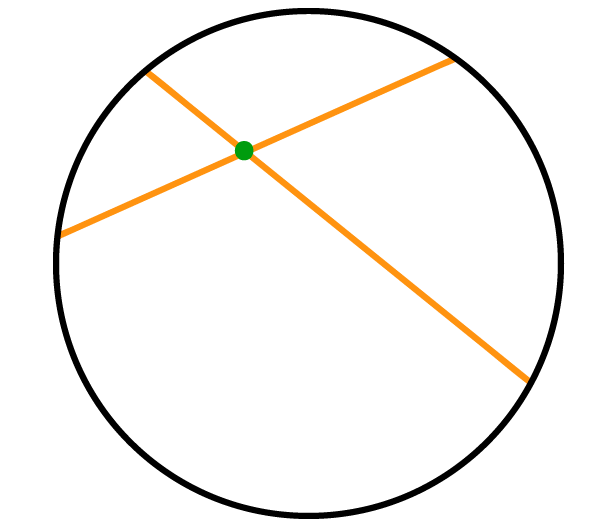
Vejam na imagem acima, que temos duas cordas se interceptando, ou se cruzando em um único ponto interno a circunferência. No fim das contas, esse ponto acaba dividindo cada uma das cordas em duas partes, cujos comprimentos podem ser representados pelas letras a, b, c, e d, como mostra a imagem abaixo:

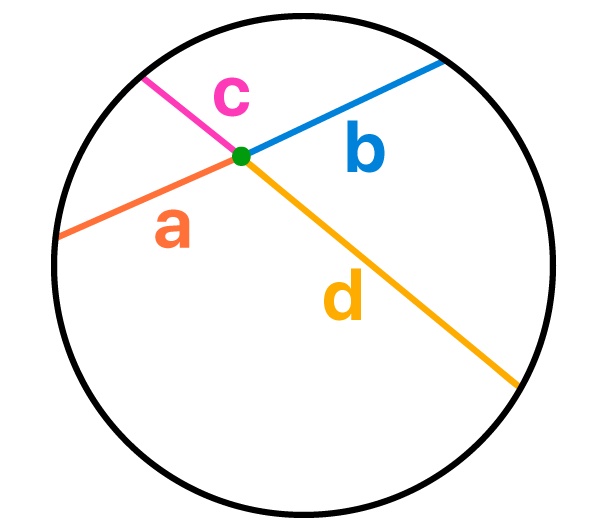
Pode não parecer, mas o fato é que esses comprimentos a, b, c, e d, podem ser relacionados, tudo de acordo com a seguinte definição:

Se duas cordas de uma mesma circunferência se interceptam, então o produto das medidas das duas partes de uma é igual ao produto das medidas das duas partes da outra.

Voltando nosso olhar para a imagem acima novamente, veremos que as medidas das duas partes de uma das cordas são representadas por a e b, enquanto que as medidas das duas partes da corda restante são representadas por c e d. Por isso, podemos “traduzir” a definição acima na seguinte fórmula:

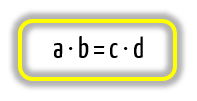
Bem tranquilo não é mesmo? Mas e se eu trouxesse à tona outra conhecida relação entre segmentos existente na geometria plana, será que eu estaria ajudando ou atrapalhando o conceito que acabamos de aprender? Isso é vocês que irão me dizer, olhem só!

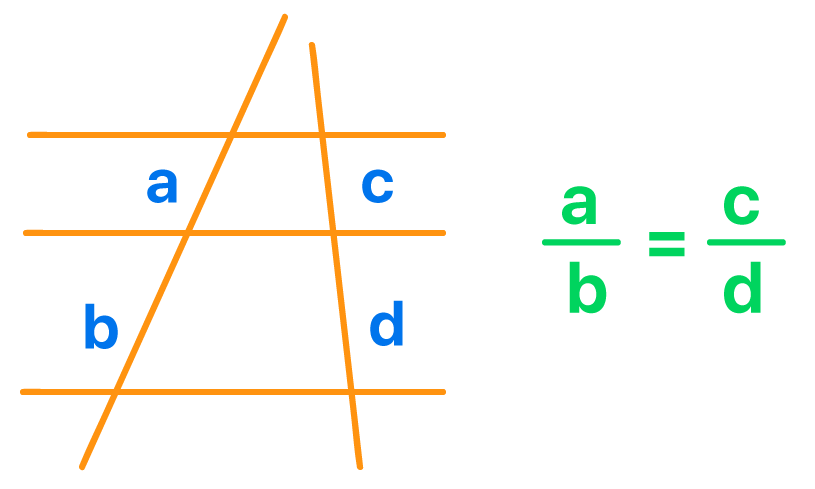
Segundo o Teorema de Tales, quando duas retas transversais interceptam um feixe de retas paralelas, diz-se que razão entre as medidas dos segmentos a e b de uma das transversais, é exatamente igual a razão entre as medidas dos segmentos c e d correspondentes na outra transversal.

Vejam pessoal, que a operação realizada entre as medidas das duas partes de uma mesma corda que intercepta uma segunda corda em um único ponto interno a uma circunferência (produto), é exatamente oposta a operação realizada entre as medidas dos dois segmentos de uma mesma reta transversal que intercepta um feixe de retas paralelas (quociente). Por isso, se vocês estão habituados a utilizar o Teorema de Tales, por favor, não confundam a sua definição com o conceito que estamos aprendendo no texto de hoje. Lembrem que uma fórmula é justamente o contrário da outra!

E agora que já afastamos o perigo, podemos continuar. Acompanhem comigo o próximo caso!

 

2º CASO: PONTO EXTERIOR – DUAS SECANTES

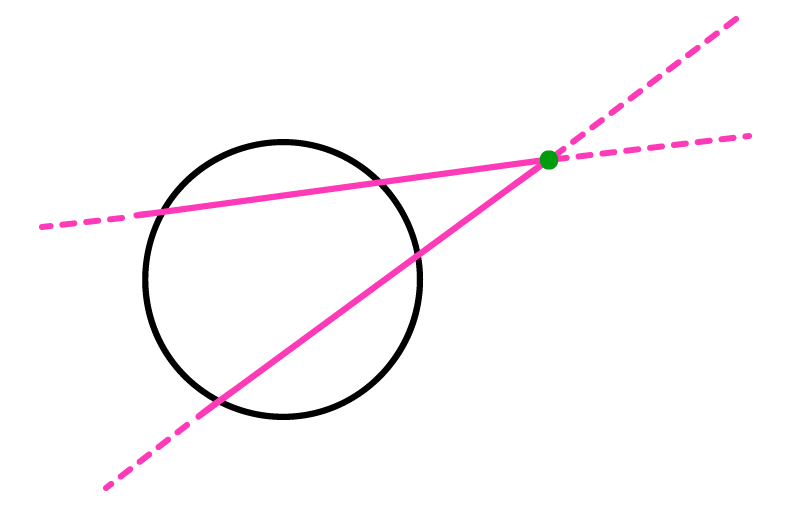
Não podemos deixar de reparar que ao contrário do caso anterior, a imagem acima nos mostra um ponto externo a circunferência, ou seja, um ponto que se localiza fora dela. É exatamente nesse ponto que duas retas secantes em relação a circunferência se interceptam, ou se cruzam. Essas retas são ditas secantes, porque cortam a circunferência em dois pontos distintos, não é mesmo?

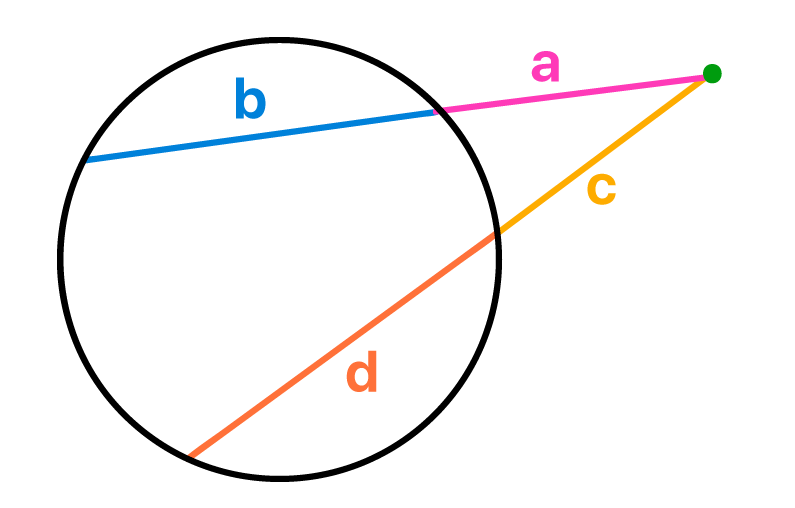
Mas o fato é que apenas alguns trechos de ambas as retas vão nos interessar nesse momento: os segmentos das retas que se encontram dentro da circunferência, cujo comprimento é dado por b e d, e também os segmentos que são externos a circunferência, e vão em direção ao ponto em que as retas se interceptam, cujo comprimento é dado por a e c. Nesse sentido, olhem só o que a definição abaixo tem a nos dizer:

Se por um ponto exterior a uma circunferência, traçarmos duas secantes a ela, então o produto da medida da primeira secante pela sua parte exterior é igual ao produto da medida da segunda secante pela sua parte exterior.

Novamente, segundo o que foi apresentado acima, nós teremos uma relação de igualdade entre dois produtos. Contudo, não podemos deixar de perceber que se tratam de produtos ou multiplicações entre a medida de toda a reta secante e a medida da sua parte externa. Ora, a medida completa de uma das retas secantes do nosso exemplo é dada pela soma entre os comprimentos a e b, enquanto que a medida completa da outra reta secante é dada pela soma entre os comprimentos c e d. Assim, podemos explicar toda essa relação através da seguinte fórmula:

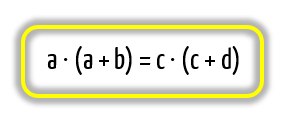
Incrível, vocês não acham? O último caso a ser abordado será muito semelhante a esse, acreditem!

 

3º CASO: PONTO EXTERIOR – UMA SECANTE E UMA TANGENTE

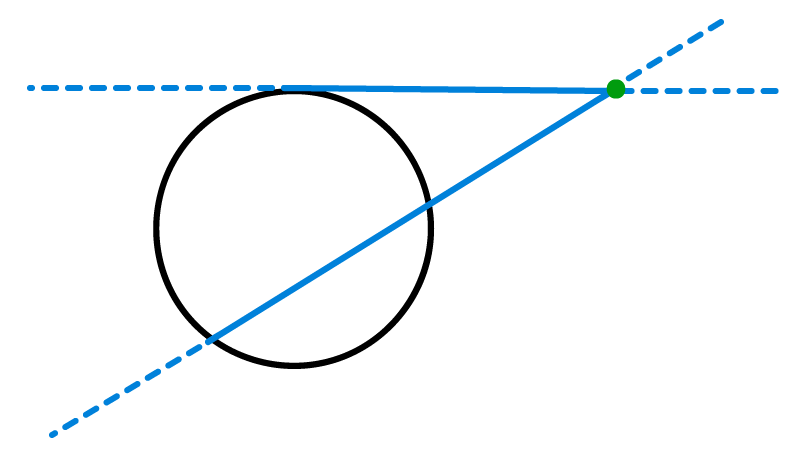
Se olhássemos a imagem acima rapidamente, poderíamos até pensar que não há diferença alguma com relação ao caso anterior. Entretanto, quem conhece o conceito de reta tangente, provavelmente percebeu que uma das retas que foram apresentadas não corta a circunferência em momento algum, mas apenas encosta nela em um único ponto. É por isso que nesse caso, diz-se que uma reta tangente e uma reta secante estão se intersectando em ponto externo a circunferência.

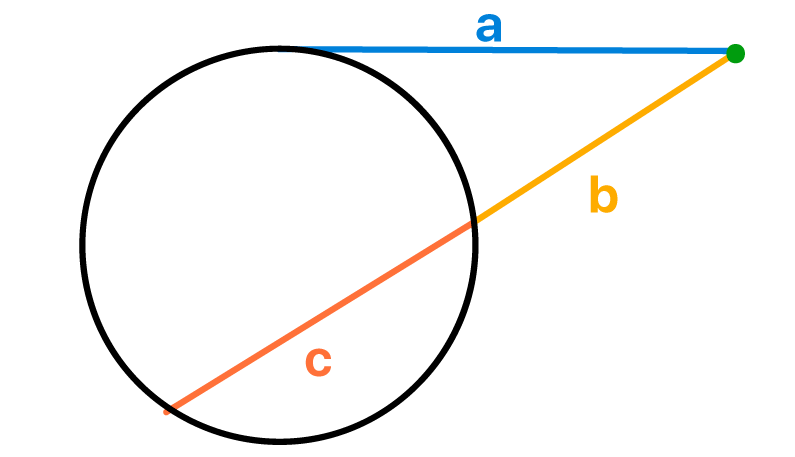
Mais uma vez, apenas alguns trechos das retas secante e tangente apresentadas vão nos interessar. A primeira delas possui um segmento interno a circunferência, cujo comprimento é dado por c, e também um segmento externo, cujo comprimento vale b. Enquanto isso, a segunda reta tem apenas um segmento externo a circunferência, cujo comprimento é igual a a. Essas observações nos permitem entender direitinho a seguinte definição:

Se por um ponto exterior a uma circunferência traçarmos uma secante e uma tangente, então o quadrado da medida da tangente é igual ao produto da medida da secante pela sua parte externa.

A única medida que a reta tangente possui é a, enquanto que a medida completa da reta secante pode ser dada pela soma entre os comprimentos b, e c. Assim, se preparem para conhecer mais uma fórmula!

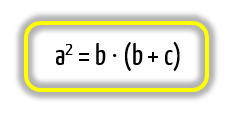
Pessoal, sempre existe um jeito de memorizar as fórmulas para não esquecer de jeito nenhum! E a notícia boa é que as fórmulas referentes aos dois últimos casos que estudamos podem ser resumidas através do seguinte macete:

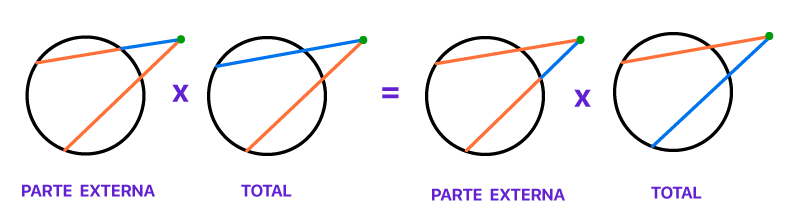
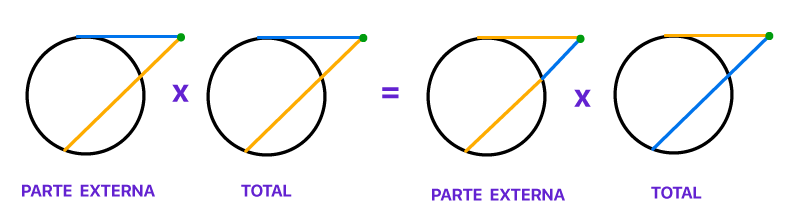
Viram que interessante? Se nós tivermos em mente a frase “parte externa vezes total”, conseguiremos relacionar as medidas das duas retas secantes e da reta secante e da reta tangente que se interceptam em um único ponto externo a circunferência! É por isso que na fórmula do último caso, temos o termo a²: quando se fala em reta tangente, a medida da parte externa é igual a medida total!

Depois de ver todo esse conteúdo, nada melhor do que resolvermos um exercício. Vem comigo aqui!

 

Determine o comprimento do raio da circunferência abaixo.

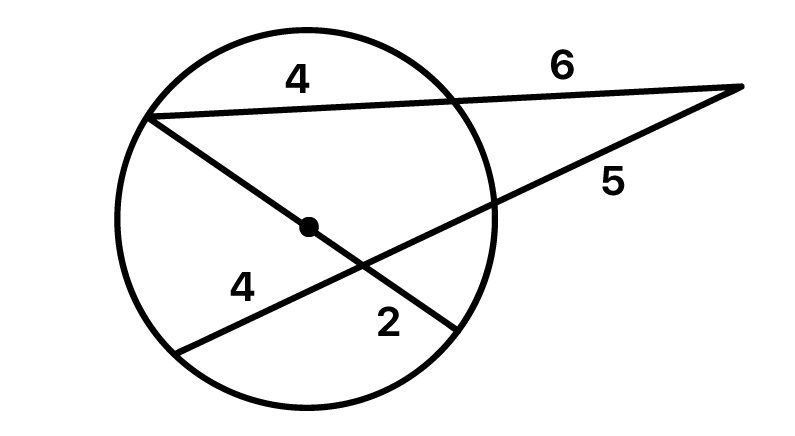
Então pessoal, o que vocês acharam de todas essas retas? Vejam que temos duas cordas, e ao mesmo tempo, duas retas secantes que se intersectam em um único ponto. Aí fica pergunta: como relacionar todos os conceitos que vimos para encontrar o raio dessa circunferência?

Se nós tentarmos resolver a questão levando em conta as medidas das cordas que se interceptam em um ponto interno a circunferência, reparem, nos faltarão duas medidas importantes. Contudo, se partirmos do ponto de vista das retas secantes, teremos mais sucesso, afinal, nos faltará apenas a medida de uma parte do segmento interno de uma das retas secantes em relação a circunferência.

Digamos agora que esse comprimento que está faltando seja dado por x. Deste modo, podemos partir para seguinte fórmula:

Parte Externa x Total = Parte Externa x Total

6 ∙ (6 + 4) = 5 ∙ (5 + 4 + x)

6 ∙ 10 = 5 ∙ (9 + x)

60/5 = 9 + x

x = 12 – 9

x = 3

 

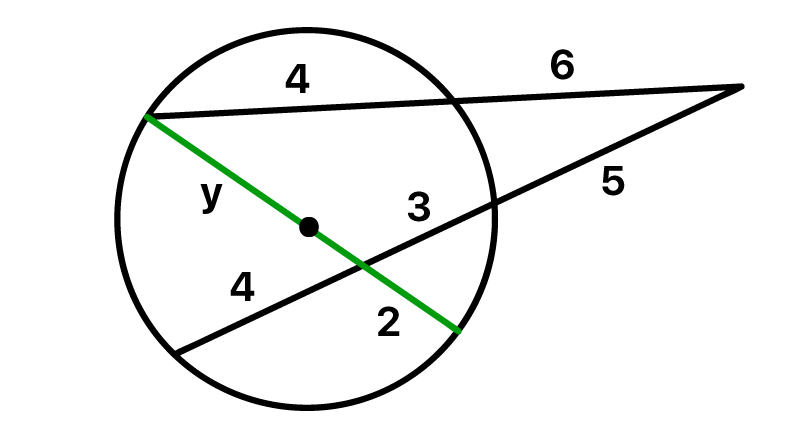
Essa nova situação nos permite enxergar com mais clareza a solução para o problema. Vejam que uma das cordas da circunferência em questão, passa exatamente sobre o centro da circunferência, portanto, o seu comprimento total corresponde ao diâmetro da mesma. Assim, se descobrirmos a medida y de uma das partes dessa corda, poderemos obter o diâmetro da circunferência com tranquilidade, e a partir dele, fica fácil de determinar o raio também, não é mesmo?

2 ∙ y = 4 ∙ 3

2y = 12

y = 12/2

y = 6

 

Diâmetro = y + 2

Diâmetro = 8

 

Raio  = Diâmetro / 2

Raio = 4

 

Como vimos no texto Conceitos iniciais sobre a circunferência e o círculo, a medida do diâmetro de uma circunferência será sempre equivalente ao dobro do comprimento do seu raio. Isso nos permitiu concluir a resolução do exercício e também o texto de hoje! Mas não se preocupem, logo logo eu estou de volta! Enquanto isso, não deixem de dar uma olhada nos exercícios que eu  resolvo no vídeo que está em anexo aqui embaixo! Por mais incrível que pareça, dá para relacionar as retas secantes e tangentes a circunferência que se interceptam em um único ponto a semelhança entre triângulos retângulos!  

Um abraço pessoal! Continuem estudando bastante matemática!