SOMA DOS TERMOS DE UMA PG FINITA

Olá pessoal, tudo bem com vocês?

No texto de hoje, vocês vão conhecer uma fórmula muito importante para a matemática: aquela que nos permite calcular a soma dos n primeiros termos de uma progressão geométrica finita! Essa fórmula é tão interessante, porque nos possibilita obter a soma dos mais diversos termos de uma sequência numérica dada na forma de uma PG, sem que seja necessário conhecer todos esses termos em si. Portanto, não deixem de acompanhar o texto! Nós vamos resolver vários exercícios sobre o assunto, e ao final dele, vocês estarão preparados para enfrentar qualquer desafio presente nas provas do ENEM e dos vestibulares!

E falando dessas temidas provas, será que vocês estão dominando todos os assuntos da matemática do ensino médio? Geometria, funções, análise combinatória, probabilidade, logaritmos, trigonometria, …, está  tudo na ponta da língua? Pessoal, não tem nada melhor do que realizar as provas do ENEM e dos vestibulares com segurança e tranquilidade, e é nesse sentido que o Professor Ferretto pode lhes ajudar! Na sua plataforma de ensino 100% online, vocês encontram videoaulas, exercícios do ENEM e dos vestibulares resolvidos em vídeo, simulados semanais, e ainda conseguem tirar todas as dúvidas com os monitores treinados pelo Professor no plano diamante. Conheçam a plataforma do Professor Ferretto! É fácil, basta acessar o site!

Agora que a dica foi dada, é hora de voltarmos a nossa atenção à estrela deste texto: com vocês, a fórmula que permite calcular a soma dos n primeiros termos de uma PG!

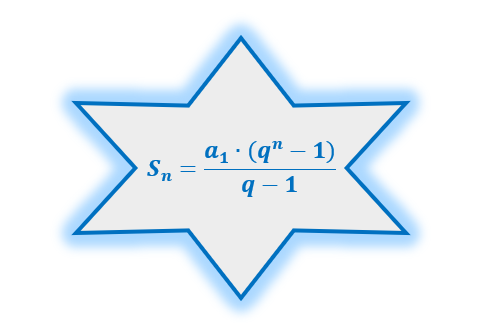
Reparem que através da fórmula acima, nós podemos calcular a soma Sn dos n primeiros termos de qualquer PG, levando em conta apenas o primeiro termo da progressão, a₁, e q, que representa a sua famosa razão. Em nenhum momento foi solicitado o valor de qualquer outro termo da sequência, como por exemplo, a₂, a₃, a₄ e aí por diante. Assim, sempre que o contexto de algum exercício abordar a soma dos termos de uma sequência cujo comportamento é de uma progressão geométrica, vocês devem procurar por 3 valores: pela quantidade de termos da sequência n, pelo seu primeiro termo a₁, e a pela sua razão q.

Querem ver como isso funciona? Então peguem seus materiais de estudo, e acompanhem comigo todos os exemplos a seguir!

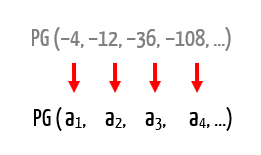
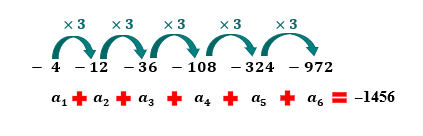
1. Dada a PG (–4, –12, –36, –108, …), determine o valor de n, para que Sn = –1456.

Observem que a sequência apresentada no enunciado (–4, –12, –36, –108, …), não possui um número finito de termos, afinal, temos a presença das conhecidas reticências, que nos dão ideia de continuidade, ou de algo que não termina. Mas a ideia nunca foi obter todos os termos dessa PG mesmo! Estamos procurando apenas pelo número n de primeiros termos necessários para que sua soma Sn seja igual ao valor –1456. Assim, se procuramos por n, e conhecemos o valor de Sn, nos resta obter os valores de a₁, e de q, a razão da PG.

Parece que quanto ao primeiro termo da sequência não há mais problema, não é mesmo? E é claro que tendo em mãos mais alguns termos da progressão, também fica fácil de determinar a sua razão q. Segundo a definição de uma PG, q pode ser obtida através da divisão ou do quociente entre dois termos consecutivos, sempre o termo da direita dividido pelo termo da esquerda, ou melhor, o termo consequente dividido pelo termo antecedente, como mostra a fórmula abaixo:

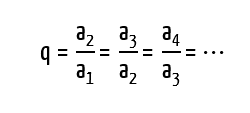
Desta forma, podemos definir a razão da progressão apresentada no enunciado facilmente, e na sequência, já podemos partir para a fórmula da soma dos termos de uma PG finita!

Pois é pessoal, quando qualquer questão que aborda a soma dos termos de uma PG nos perguntar o valor de n, é provável que possamos cair em uma situação como essa: n está no expoente da razão q, o que pode dar origem a uma equação exponencial. Mas não se preocupem muito não: sempre que isso acontecer, vocês devem usar o conceito de igualdade de potências de mesma base. Uma vez que as bases das potências são iguais, é possível desconsiderá-las e apenas igualar seus expoentes.

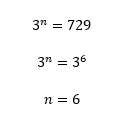
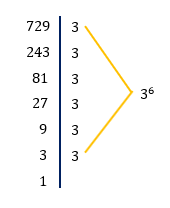
Bem tranquilo, vocês não acham? É claro que quem está acostumado a resolver equações exponenciais, possivelmente sabe de cor que 729 é igual a 3 elevado na sexta potência. Mas não é necessário memorizar essas conversões: ao fatorar 729, vocês encontram facilmente o seu valor na forma de potência.

Bom, para concluirmos nosso primeiro exemplo com qualidade, nada melhor do que interpretarmos direitinho o que o resultado obtido quer nos dizer. Agora, sabemos que somando os 6 primeiros termos da progressão geométrica, nós obtemos –1456.

Entendido? Esse foi fácil, não é mesmo? Vamos ao próximo exemplo então!

2. Se S₃ = 21 e S₄ = 45 são, respectivamente, as somas dos três e quatro primeiros termos de uma PG, cujo termo inicial é 3, determine a soma dos cinco primeiros termos da progressão.

Que enunciado mais confuso, vocês não acham? A princípio, a única coisa que está mais clara aí, é que o valor do termo inicial, ou do primeiro termo da PG, o a₁ é igual a 3. Outra informação que não podemos deixar passar, é que como está sendo questionada a soma dos 5 primeiros termos da PG, S_­­5, então a quantidade de termos cuja soma será calculada, o n, deve ser igual a 5. Como a razão q da progressão não está aparente, nós precisaremos desvendar o que os dados das somas dos 3 e 4 primeiros termos da PG em questão podem nos mostrar:

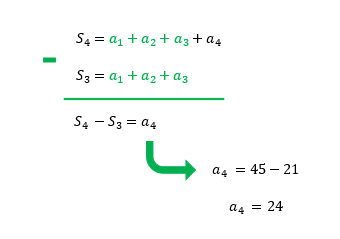
E não é que essas informações nos levaram ao encontro do quarto termo da sequência? Pode não parecer, mas esse dado é muito valioso. Sempre que temos a nossa disposição o valor de quaisquer dois termos de uma progressão geométrica, nós podemos calcular a sua razão q através da conhecida fórmula do termo geral de uma PG, como mostra a imagem abaixo:

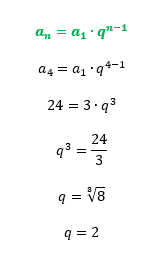
Feito, agora basta partirmos para a fórmula que deu origem ao texto de hoje, e chegaremos ao valor da soma dos 5 primeiros termos da sequência desejada:

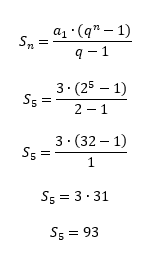
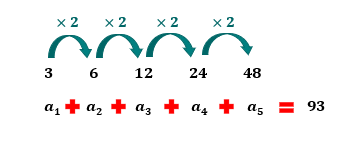
Até aí tudo tranquilo? Agora, nós vamos partir para a uma aplicação um pouco mais prática do assunto. A verdade é que a progressão geométrica tem uma relação muito próxima com os conceitos de aumentos e descontos, que envolvem porcentagem. O nosso último exemplo lhes ajudará a interpretar questões que envolvem esses temas. Vem comigo aqui!

3. Em uma fábrica de calçados, entre os anos de 2011 e 2015, a produção aumentou 10% ao ano. Sabendo que a produção em 2011 foi de 20 000 calçados, determine a quantidade total de calçados produzidos nesses cinco anos.

E aí, o que acharam desse novo contexto? A princípio, eu sei, parece complicado entender quais dessas informações tem relação com a soma dos termos Sn, com a quantidade de termos n, com a razão q, ou mesmo com o primeiro termo a₁ de uma determinada progressão geométrica. Mas não se preocupem, vamos esmiuçar todos os detalhes importantes deste exemplo até chegarmos na fórmula que temos utilizado, fiquem atentos!

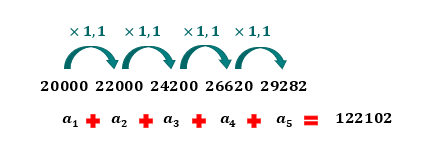
O enunciado pede que determinemos a quantidade total de calçados produzidos durante 5 anos. Para obter esse valor, nada mais justo do que somar a produção de calçados de 2011, 2012, 2013, 2014 e 2015, não é mesmo? Assim, podemos concluir que a quantidade de calçados produzida a cada ano representa cada um dos termos da PG, e que estamos procurando por Sn, ou melhor, por S₅, afinal, 5 anos de produção serão analisados.

Temos o valor de n, de a₁, procuramos por Sn, mas cadê a razão q da progressão? Pois é pessoal, é aí que entra a questão da porcentagem. Diz-se no enunciado, que a produção aumentou 10% ao ano entre 2011 e 2015. Assim, para sabermos quantos calçados foram produzidos em 2012, 2013, 2014 e 2015, basta multiplicarmos a produção de cada ano por 1,1.

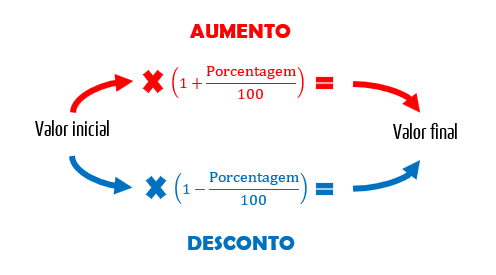
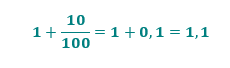
A imagem acima não deixa dúvidas de que 1,1 é a razão q desta PG. Portanto, já podemos encontrar a produção total de calçados da fábrica ao final de 5 anos através da fórmula da soma dos termos de uma progressão geométrica finita.

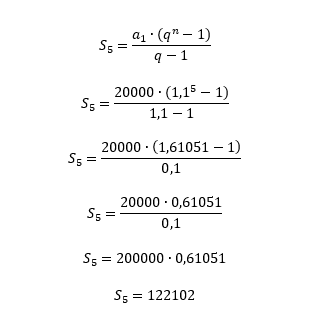
E aí pessoal, tudo entendido? Abaixo temos um vídeo em anexo, em que vocês poderão acompanhar mais alguns exemplos resolvidos, e aprofundar um pouquinho aquele conceito de aumentos e descontos que acabamos de ver. Digo isso, porque como sempre, uma hora o texto chega ao fim! Mas espero que vocês tenham gostado da abordagem, e que esse assunto os instigue a estudar cada vez mais a progressão geométrica e a matemática como um todo!

Um abração a todos! Tenham muito sucesso nos estudos!