TEOREMA DE PITÁGORAS
31/01/2020
O Teorema de Pitágoras é um dos mais famosos teoremas da matemática. De acordo com este teorema, em qualquer triângulo retângulo, a soma dos quadrados das medidas dos catetos é igual ao quadrado da medida da hipotenusa.
Olá, pessoal! Como vão?
Em um tempo não muito distante, nós estudamos aqui no blog os elementos do triângulo retângulo, o conceito de semelhança entre triângulos retângulos e também as chamadas relações métricas no triângulo retângulo. Só que uma dessas relações, por sinal, a mais famosa delas, ainda não foi mencionada: o Teorema de Pitágoras! Vamos dedicar esse texto inteirinho a ela, porque quem conhece as demais relações métricas no triângulo retângulo e o Teorema de Pitágoras, não erra mais nenhuma questão do ENEM ou dos vestibulares que envolve os triângulos retângulos.
O Teorema de Pitágoras pode ser demonstrado de centenas de maneiras diferentes. No próximo item, nós vamos conhecer uma dessas demonstrações. Sigam comigo!
1. UMA DAS DEMONSTRAÇÕES DO TEOREMA DE PITÁGORAS

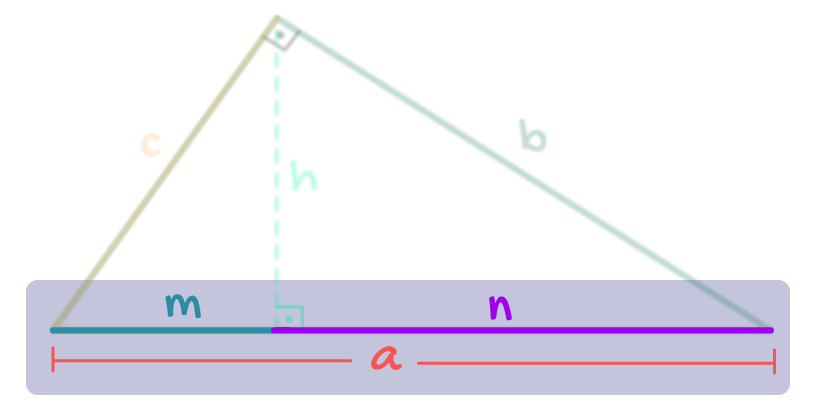
Vamos começar relembrando outras duas relações métricas no triângulo retângulo que serão muito importantes no processo de demonstração do Teorema de Pitágoras. Lá vem o famoso triângulo retângulo e seus elementos novamente!
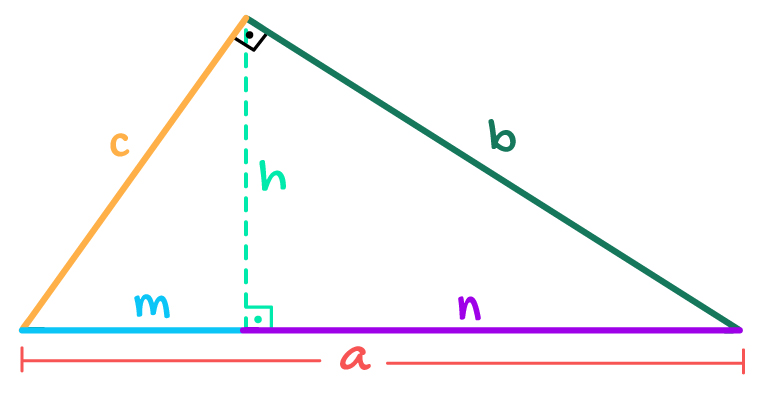
Considerando o triângulo acima, é possível dizer que “o quadrado da medida de um cateto (c ou b) é sempre igual ao produto entre a medida de sua projeção sobre a hipotenusa (m ou n) e a própria medida da hipotenusa a”. Nós estudamos essa ideia com detalhes aqui. Em forma de equação, tem-se o seguinte:
c2 = m ∙ a
b2 = n ∙ a
Até aí tudo tranquilo, pessoal? Então, convido vocês a somar essas duas equações que obtivemos termo a termo. O resultado vai ser bem interessante, eu garanto!
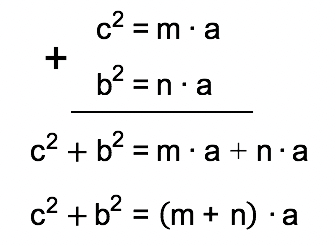
Sendo a um fator comum entre os termos m∙a e n∙a, este foi colocado em evidência. Assim, formou-se uma igualdade entre a soma dos quadrados dos catetos b e c, e o produto entre a hipotenusa a e a soma das projeções dos catetos sobre a hipotenusa m e n.

Então, pessoal, se vocês voltarem novamente a atenção para o triângulo retângulo que nos leva a todas a relações métricas conhecidas, verão que a medida equivalente a soma das projeções dos catetos sobre a hipotenusa m e n é a própria medida da hipotenusa a!
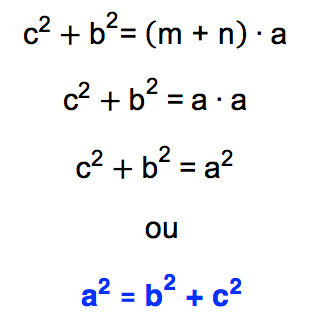
Pronto! Chegamos ao Teorema de Pitágoras!
2. INTERPRETAÇÃO GEOMÉTRICA DO TEOREMA DE PITÁGORAS
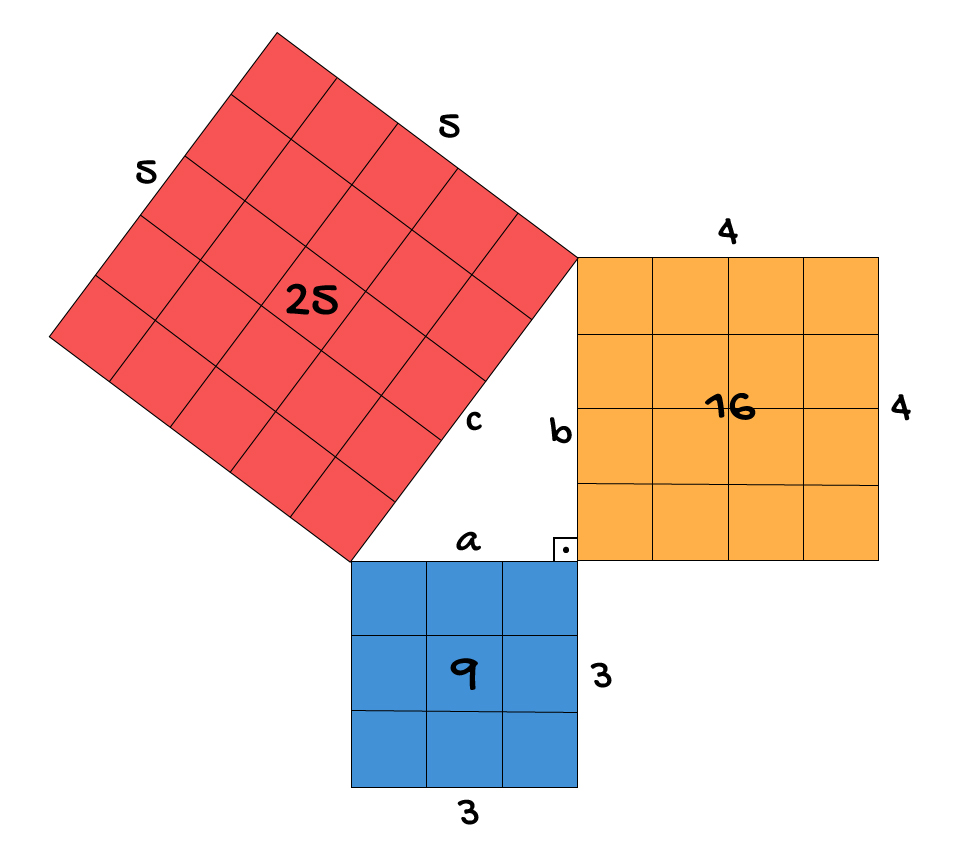
Ao estudar o Teorema de Pitágoras, provavelmente vocês já se depararam com imagens parecidas com essa que vemos acima. Mas como compreender a sua real relação com o Teorema de Pitágoras? É isso que entenderemos agora!
O Teorema de Pitágoras é constantemente descrito através da frase: “a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa”. Pois então, se vocês pensarem no termo “quadrado” não como um valor elevado a potência 2, mas como o quadrado em si, é possível chegar a seguinte situação:
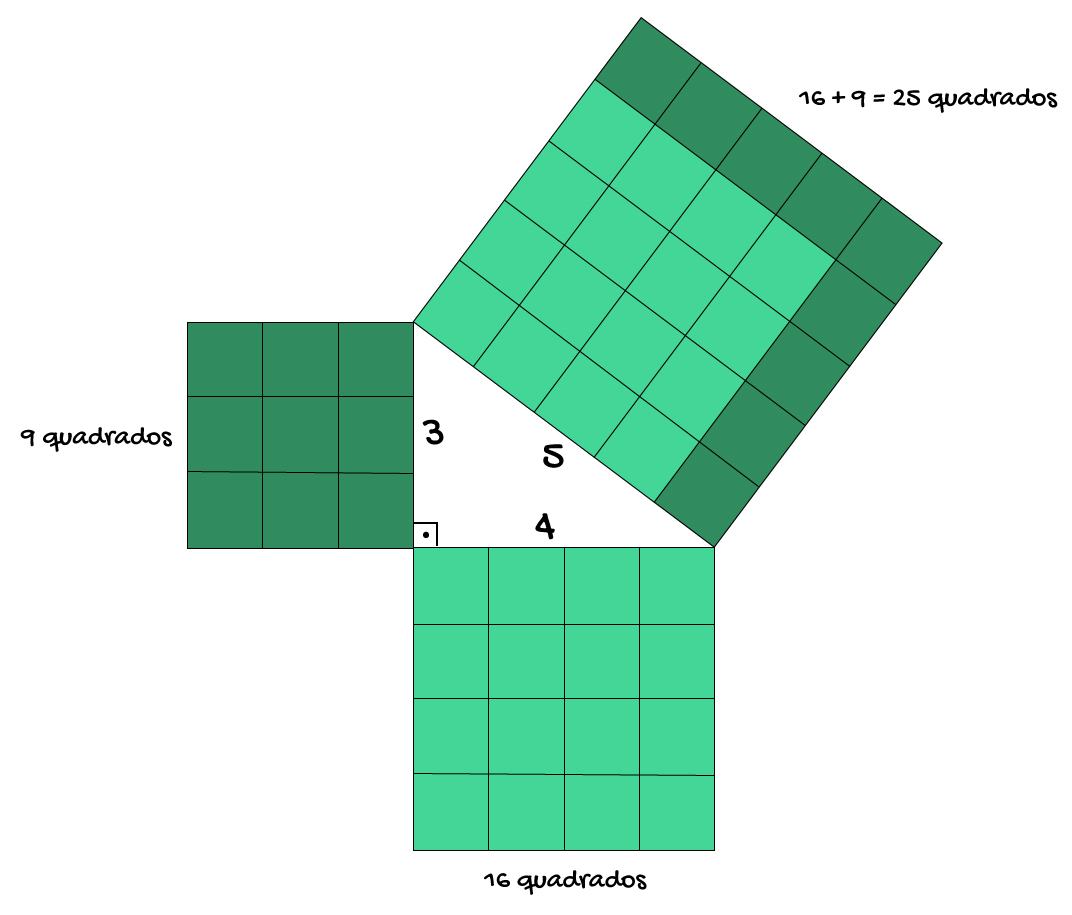
Considerando que a medida a da hipotenusa seja 5, e que a medida dos catetos b e c seja 4 e 3, podemos desenhar quadrados de lado 5, 4 e 3 próximo aos lados do triângulo retângulo. Estes quadrados, por sua vez, podem ser divididos em outros 25, 16 e 9 quadrados de lado igual a 1. Pois bem, se pudéssemos destacar cada um dos quadrados formados nos catetos, poderíamos montar tranquilamente o quadrado gerado pela hipotenusa.
Incrível, não é mesmo? Agora que já conhecemos todas as relações métricas do triângulo retângulo, podemos praticar esse conhecimento com exercícios. Vem comigo!
3. EXERCÍCIO RESOLVIDO QUE ENVOLVE O TEOREMA DE PITÁGORAS

Calcule o valor de x, y e z no triângulo abaixo:
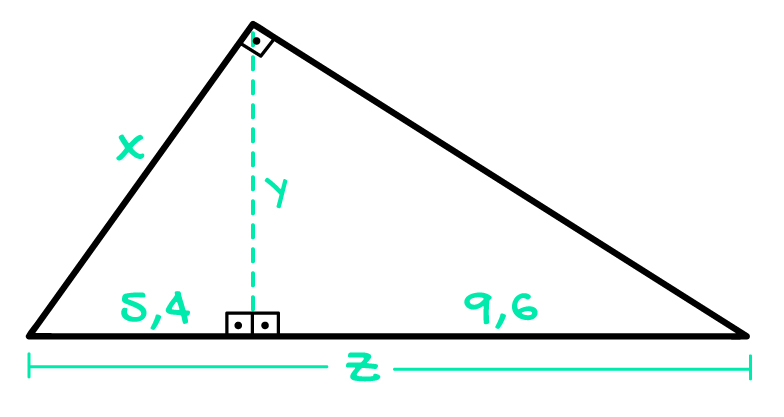
Reparem no triângulo retângulo acima. Os únicos valores que nos são entregues são as medidas das projeções dos catetos sobre a hipotenusa m e n. Tendo isso em vista, podemos encontrar facilmente a medida de z, que representa a hipotenusa do triângulo retângulo:
z = 5,4 + 9,6
z = 15
Bom, temos a medida da hipotenusa do triângulo, que é 15. Contudo, ainda não conhecemos a medida dos catetos deste triângulo. Isso significa que o Teorema de Pitágoras não é a relação métrica mais indicada para continuarmos a resolução. Então, que tal relembrarmos outras 4 relações métricas que certamente poderão nos ajudar?
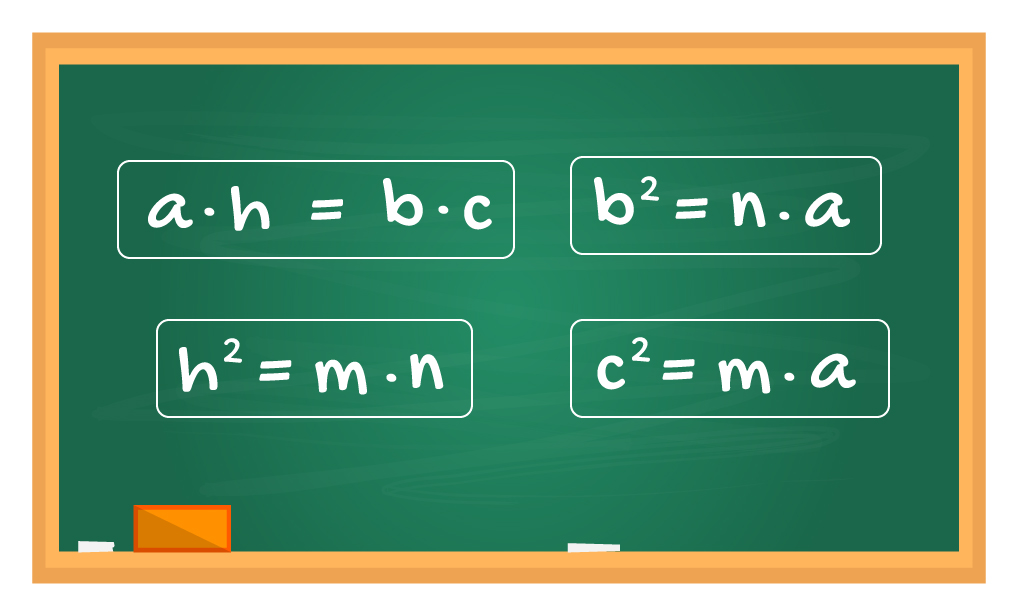
Agora sim! Observem no quadro que existe uma relação entre a altura do triângulo retângulo h e as projeções dos catetos sobre a hipotenusa m e n. Neste exercício, h é a incógnita y que estamos procurando, e m e n são conhecidos. Portanto, não há melhor forma de encontrarmos o valor de y!
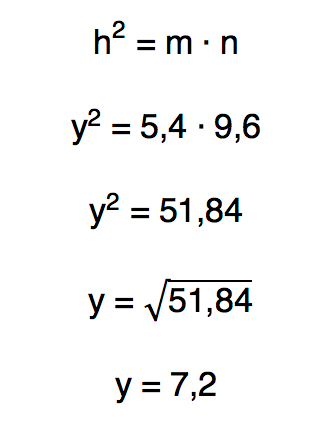
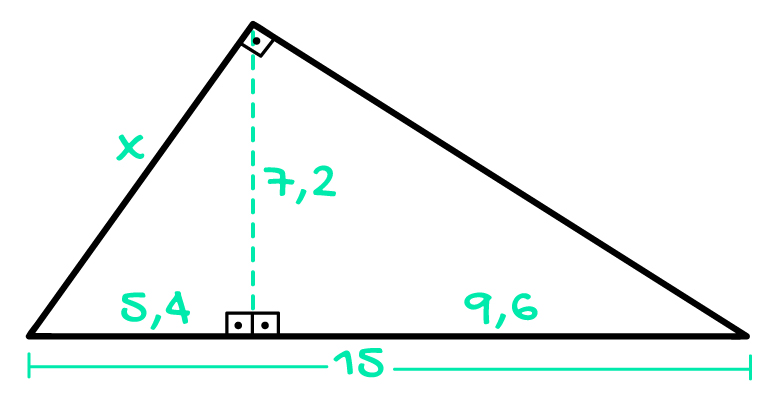
Conhecer o valor de y nos possibilita determinar o valor de x facilmente. Isso porque se repararmos melhor no triângulo retângulo acima, veremos que ele é divido em outros dois triângulos retângulos. O mais da esquerda, cuja medida da hipotenusa vale x, possui dois catetos de medidas conhecidas: 5,4 e 7,2. Portanto, finalmente podemos aplicar o Teorema de Pitágoras na resolução!
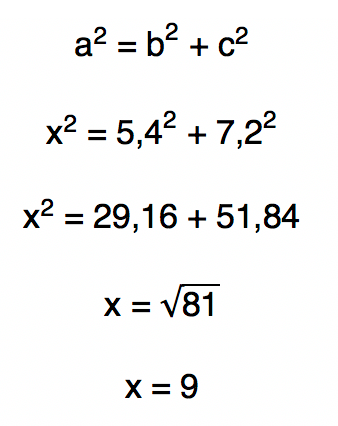
Beleza pessoal!? Agora que conhecemos as principais relações métricas do triângulo retângulo e sabemos aplica-las, está na hora de encerrarmos o texto. Venham comigo!
Finalizando com duas super dicas
Pessoal, espero que este texto tenha sido muito proveitoso para os estudos de vocês. E como sempre é tempo de revisar e complementar os estudos, deixo em anexo um vídeo sobre as relações métricas no triângulo retângulo. O vídeo traz a teoria e mais alguns exercícios que envolvem este assunto. Não deixem de conferir!
Ahh… E se você curtiu este texto, aproveite também para saber como a plataforma do Professor Ferretto funciona! É só clicar aqui!
Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!
Abração! Espero vocês no próximo post!