DETERMINANDO A FUNÇÃO DO 1º GRAU
24/08/2018
Olá pessoal! Tudo bem?
Vocês sabiam que é possível determinar uma função do primeiro grau, ou uma função afim, sem saber os valores numéricos dos seus coeficientes a e b? Para isso, basta conhecer o valor da função em dois pontos distintos. Então pessoal, se vocês ainda não sabem o que são os valores de uma função afim, ou como utilizá-los para determinar uma função do 1º grau, acompanhem esse texto, pois nós estudaremos tudo isso! E olhem só que interessante: hoje nós também abordaremos como resolver sistemas de equações pelo método da adição e da substituição, algo extremamente importante para quem vai prestar as provas do ENEM e dos vestibulares logo mais!
Os conceitos da função afim, são muito cobrados nas provas de matemática do ENEM e dos vestibulares, porque envolvem tudo aquilo que possui um comportamento linear. Por isso, se o objetivo de vocês é estar bem preparado para ter um ótimo aproveitamento em provas como essas, não dá mais para perder tempo: assinem logo a plataforma do Professor Ferretto! Lá vocês encontram um curso de matemática completo e 100% online, onde as aulas são gravadas, o que permite que vocês estudem na hora que desejarem!
E claro, para que seja possível praticar tudo o que é visto na teoria, é disponibilizado um material de apoio com centenas de downloads, que garantem uma evolução imensa quando o assunto é a interpretação das questões. Eu sempre digo, é muita vantagem para citar aqui! Por isso, não deixem de acessar o site, e conheçam todos os benefícios e os bônus que vocês garantem ao comprar qualquer plano do Professor Ferretto!
Feito pessoal!? Então, eu imagino que vocês conheçam a fórmula que é apresentada na figura abaixo:
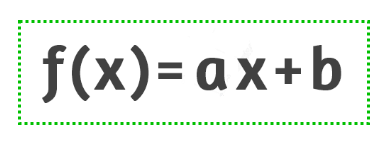
Essa expressão representa a função do primeiro grau! Pode não parecer, mas é possível extrair dela uma série de informações, muitas das quais nós já estudamos aqui no blog, e que vocês podem acompanhar dando uma olhada na categoria Função Afim. Mas hoje, apenas dois termos vão ganhar a nossa total atenção: os coeficientes a e b.
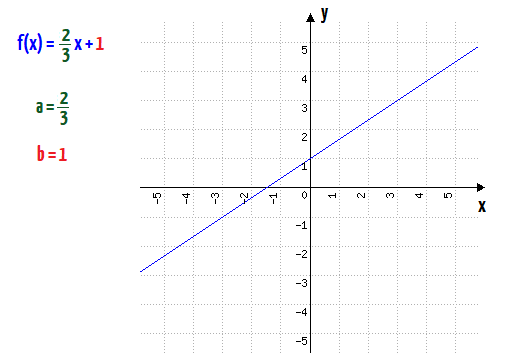
Na imagem acima, nós pudemos ver um exemplo de função do 1º grau. Essa função possui um valor numérico para o coeficiente a, e outro para o coeficiente b, além de claro, uma forma gráfica. Agora observem esse outro exemplo abaixo com atenção:
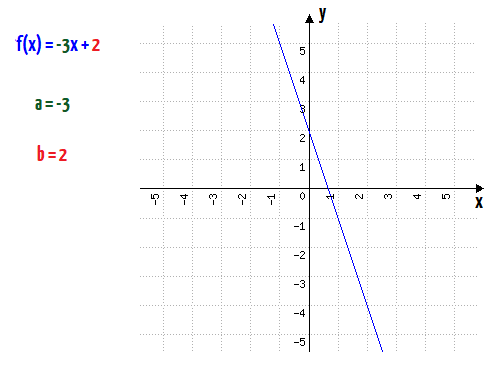
Vejam que essa função possui valores diferentes para os coeficientes a e b, e também uma forma gráfica diferente do exemplo anterior. Então, se vocês ainda não mataram a charada, entendam o seguinte: os coeficientes a e b são quem determinam, ou quem definem a função do primeiro grau! Você aí, com certeza tem características que te definem, ou que te tornam diferente das outras pessoas. O mesmo acontece na função afim: cada função possui uma forma gráfica diferente, inteiramente determinada por seus coeficientes a e b.
É necessário conhecer os coeficientes a e b para determinar uma função do 1º grau.
Portanto, tem-se um problema quando o enunciado dos exercícios não informa os valores numéricos de a e b. Ops! Na verdade não haverá problema algum, desde que sejam conhecidos pelo menos dois valores da função afim. Vocês vão aprender na sequência, quem são esses valores, e como utiliza-los para determinar a função do primeiro grau. Vem comigo aqui!
1. VALOR DE UMA FUNÇÃO AFIM

O valor de uma função afim é o valor que a função assume para um determinado x.
Para compreendermos com clareza a definição acima, vamos utilizar um exemplo.
Considerando a função f(x) = 3x + 1, determine:
a. f(1)
b. f(–2)
Para calcular f(1), basta substituirmos o valor de x na função por 1, vejam só:
f(x) = 3x + 1
f(1) = 3∙1 + 1
f(1) = 3 + 1
f(1) = 4
O mesmo deve ser feito no item b, ou seja, para calcular f(–2), basta substituir agora, o valor de x na função por –2.
f(x) = 3x + 1
f(–2) = 3∙(–2) + 1
f(–2) = –6 + 1
f(–2) = –5
Nesses dois exemplos, vejam que a função f(x) = 3x + 1, assumiu valores diferentes para cada valor de x que foi atribuído. Quando substituímos x por 1, a função assumiu o valor 4; já quando substituímos x por –2, a função assumiu o valor –5. Isso significa que 4 é o valor da função quando x é igual a 1, da mesma forma que –5 é o valor da função quando x é igual –2.
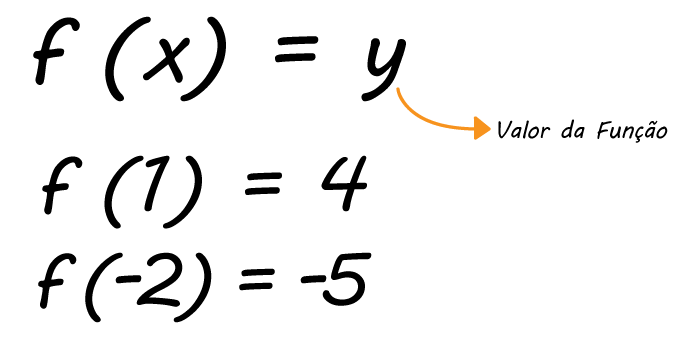
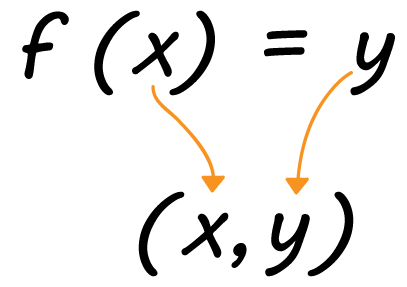
Talvez fique ainda mais fácil associar a ideia de valor de uma função afim aos pontos, ou coordenadas cartesianas que utilizamos para construir os gráficos da função do primeiro grau. Eles são dados sempre na forma de par ordenado (x, y). Aí é só pensar no seguinte: o valor de uma função afim é igual ao valor de y encontrado quando um determinado x, o mesmo ali da coordenada, é atribuído a esta função.
2. DETERMINAÇÃO DA FUNÇÃO DO 1º GRAU CONHECENDO-SE SEUS VALORES EM DOIS PONTOS DISTINTOS
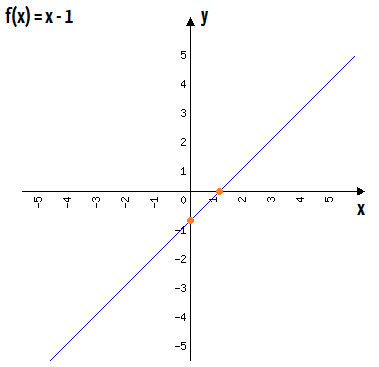
É fato que quando se conhece uma função do 1º grau, dois pontos são suficientes para determinar a sua forma gráfica. Então por que o contrário não poderia ser verdadeiro? Pois bem, de posse de apenas dois pontos ou valores de uma função afim, é possível determinar essa função. O método consiste em substituir esses dois pontos ou valores dados, na fórmula característica da função do 1º grau, a f(x)=ax+b. Isso dará origem a duas equações, cada uma com duas incógnitas, que são, claramente, os valores de a e b. Mas não há problema algum quanto a esse detalhe: basta montar um sistema e escolher o método de preferência para resolvê-lo. Assim, em poucos instantes chega-se ao valor de a e b, e é claro, a função do primeiro grau formada por eles.
Bom, se você acabou de ler as informações acima, mas nenhuma luz brilhou no fim do túnel, acalme-se: vamos fazer um exemplo e tudo ficará literalmente mais claro. Vem comigo aqui!
Determine a função do 1º grau, sabendo que f(–1) = 3, e f(2) = 2.
De acordo com o que nós estudamos acima, se é dito que f(–1) = 3, e que f(2) = 2, significa que 3 é o valor da função ou o valor de y quando x é igual a –1, da mesma forma que 2 é o valor da função ou o valor de y quando x também é igual a 2.
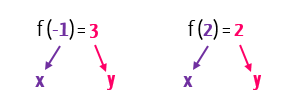
Esses dados nos permitem substituir, respectivamente, os valores de x e de y da fórmula característica da função do 1º grau, por –1 e 3, e também por 2 e 2, formando duas equações cujas incógnitas serão a e b.
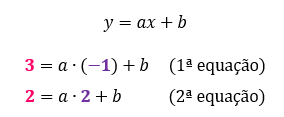
Organizando as equações:
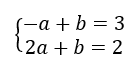
Ora, e não é que houve a formação de um sistema mesmo!? Pois bem, existem dois métodos muito simples que possibilitam a resolução de sistemas como esse: o método da substituição, e o método da adição. Nós vamos utilizar este exemplo para compreendermos a resolução de um sistema através do método da substituição:
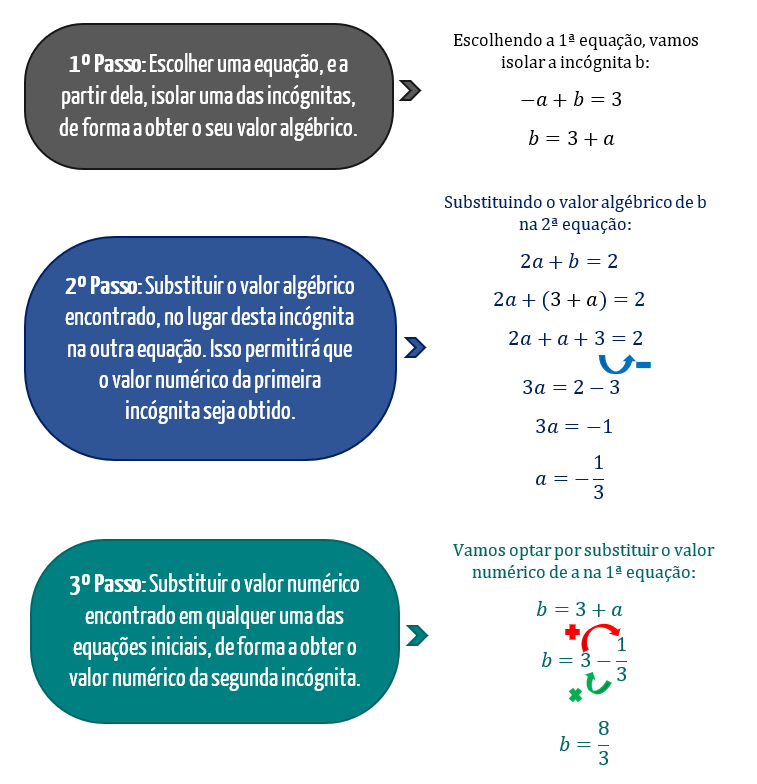
Desta forma, a função f(x) = ax + b pode finalmente ser determinada:
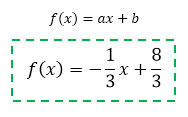
Tranquilo, não é mesmo? Vamos fazer mais um exemplo para consolidar o nosso aprendizado.
Determine a função do 1º grau que passa pelos pontos A (1,5) e B (–3, –7).
Vejam que nesse caso, os dois pontos da função do primeiro grau que devemos determinar, são dados na forma de pares ordenados, e não de valores. Mas nós vimos neste texto, que os dois modos são válidos, porque claro, desde que tenhamos em mãos dois valores de x e de y para substituirmos na expressão característica da função afim, nosso sistema estará garantido, e aí é só uma questão de tempo para encontrarmos os valores dos coeficientes a e b, que poderão determinar a função.
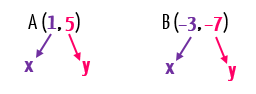
Então, sem mais delongas, vamos substituir, respectivamente, os valores de x e de y da fórmula característica da função do 1º grau, por 1 e 5, e também por –3 e –7, formando duas equações cujas incógnitas serão a e b.
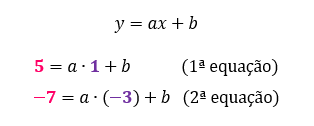
Organizando as equações:
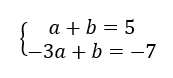
Está aí o nosso sistema! Mas desta vez, nós vamos resolvê-lo utilizando o método da adição. Esse método é um tanto diferente do anterior, porque como o próprio nome sugere, ele visa somar as duas equações do sistema, de forma a eliminar ou cancelar uma de suas incógnitas. Vejam como é simples somar as equações do sistema do nosso exemplo:
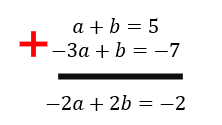
Mas olhem que coisa engraçada, nós somamos as duas equações do sistema, e mesmo assim, não conseguimos eliminar nenhuma das incógnitas! Pois é pessoal, infelizmente, na maioria dos sistemas, somar as duas equações pode não ser o suficiente para eliminar uma das incógnitas. Em casos como esses, é necessário utilizar alguns artifícios matemáticos, que em conjunto com a soma das equações, possibilitarão o cancelamento de uma das incógnitas.
Querem um exemplo do que isso significa? Pois bem, e se antes de somarmos as equações do sistema, nós multiplicássemos toda a primeira equação por –1?
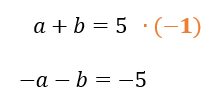
Reparem só no que iria acontecer:
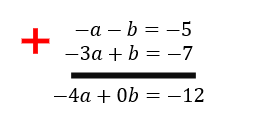
E não é que dessa maneira foi possível eliminar a incógnita b? Mas e se ao invés disso, nós tivéssemos multiplicado toda a primeira equação por 3, o que aconteceria?
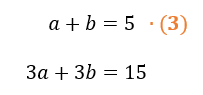
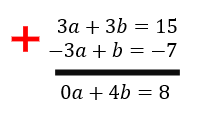
Ora, vejam que desta forma nós conseguimos eliminar a incógnita a! Que interessante não é mesmo? Então pessoal, utilizar um artifício matemático aqui, significa multiplicar ou dividir toda uma equação por um valor numérico apropriado, que torne possível o cancelamento de uma das incógnitas quando for realizada a soma das equações. É importante lembrar também, que multiplicar ou dividir toda uma equação por um mesmo valor, não altera a característica inicial do sistema, porque as proporções entre os valores irão se manter. Só não dá para esquecer de fazer isso antes e depois da igualdade, certo?
Tendo isso em vista, é claro que poderiam surgir outras maneiras de cancelar uma das incógnitas desse sistema do exemplo. Pode-se trabalhar até mesmo com uma modificação na segunda equação, sem problema algum. Tudo o que vocês devem fazer sempre, é observar o valor numérico que acompanha a incógnita que desejam eliminar em uma das equações, e em seguida, trabalhar na outra equação com o intuito de obter um valor numérico de mesmo módulo, mas de sinal oposto àquele valor observado, como fizemos acima, onde tínhamos 1 e -1 e depois 3 e -3.
Agora eu sinto que vocês já estão preparados para acompanhar o esquema que nos levará a solução desse sistema pelo método da adição. Vamos lá então!

Assim, é possível determinar uma nova função do 1º grau:
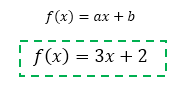
E aí pessoal, conseguiram entender a ideia? A grande verdade é que estudamos apenas dois métodos de resolução de sistemas de equações, mas cada um deles pode gerar inúmeras formas de resolução, porque tudo depende das decisões que o aluno toma ao simplificar, isolar, somar, substituir e por aí vai… Assim, deixo como tema de casa a seguinte tarefa: tentem resolver os sistemas destes exemplos utilizando estratégias diferentes. Pode ser que as resoluções de vocês fiquem ainda mais simples! E como sempre, aqui no final do texto, eu deixo um vídeo em anexo. Deem uma olhada nele, porque as abordagens são diferentes, e uma sempre complementa a outra! No mais, espero que esse assunto tenha contribuído bastante para o conhecimento de vocês, e que possa lhes ajudar a desenvolver o raciocínio lógico da matemática!
Abração! Tenham ótimos estudos aí e até breve!