
Os assuntos de biologia que mais caem no Enem são uma das preocupações de quem está se preparando para a...

Você sabe como encontrar os valores reais que podem satisfazer, ao mesmo tempo, duas inequações diferentes? Vem comigo aqui e entenda tudo sobre as inequações simultâneas!
Olá pessoal, tudo bem por aí?
Algo que é simultâneo, se realiza ao mesmo tempo. Por isso, no texto de hoje, vocês vão aprender nada mais nada menos do que encontrar uma solução que possa satisfazer duas ou mais inequações do primeiro grau ao mesmo tempo! Mas para que isso seja possível, é muito importante que vocês saibam tudo sobre os intervalos reais e sobre as operações que envolvem esses intervalos, dando ênfase ao conceito de intersecção. Como todo esse conteúdo já está disponível aqui no blog, vocês podem ficar tranquilos: o assunto estará dominado até a chegada das temidas provas dos vestibulares!
E falando nos vestibulares, vocês sabiam que na plataforma do Professor Ferretto tem tudo sobre trigonometria, geometria espacial, geometria analítica, matrizes, números complexos, e até aulas de aprofundamento que envolvem o estudo das cônicas e da geometria de posição? Pessoal, são 25 módulos cheinhos de conteúdo que abrangem toda a matemática do ensino médio! Isso que nem falamos dos mais de 1000 exercícios do ENEM e dos vestibulares resolvidos em vídeo, dos simulados semanais, das aulas de física… Eu, se fosse vocês, acessava o site e conferia todas as vantagens que o curso de matemática do Ferretto pode oferecer!
Bom, o nosso objetivo aqui é fazer com que as inequações simultâneas do 1º grau não sejam mais um problema para ninguém. Nesse sentido, não existem palavras que possam descrever melhor a resolução de inequações do que os velhos e bons exemplos numéricos. É por isso que resolveremos vários deles agora. Vem comigo aqui!
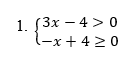
Uma das formas em que podemos encontrar inequações simultâneas, é exatamente essa que vemos acima: através de um sistema. Só que ao invés de termos a presença de duas incógnitas e dos sinais de igualdade, como em um sistema de equações comum, nós temos a presença de duas inequações do 1º grau que utilizam a mesma incógnita x. Assim, o fato das duas estarem relacionadas na forma de sistema, só pode significar uma coisa: precisaremos encontrar valores de x que satisfaçam ambas as inequações.
Sabem o porquê de tudo isso? Digamos que vocês fossem resolver as duas inequações acima separadamente. Segundo o texto Introdução à Inequação do 1º Grau, isso poderia ser feito assim:
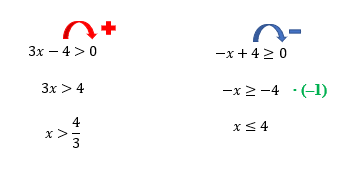
Vejam, a solução da primeira inequação é formada por todos os valores de x maiores do que 4/3, que na forma decimal, é a dízima periódica 1,333333… Isso significa, que se qualquer valor maior que 4/3 substituir o lugar de x na inequação 3x – 4 > 0, ela resultará em um valor maior que zero, exatamente como deve ser. O mesmo acontece com a segunda inequação: sua solução é formada por todos os valores de x menores ou iguais a 4. Isso significa, que se qualquer valor menor ou igual a 4 substituir o lugar de x na inequação –x + 4 ≥ 0, ela resultará em um valor maior ou igual a zero, como foi determinado.

Mas será que todos os valores reais que representam a solução de uma das inequações são, ao mesmo tempo, uma solução viável para a outra inequação? Ora, podemos descobrir isso através de mais um teste simples: substituiremos o valor 5, que é solução para a primeira inequação na segunda inequação, e vice-versa. Fiquem atentos ao que irá acontecer.
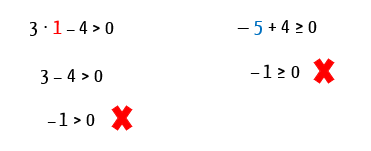
Pois é, parece que nem todo valor real que é solução para uma inequação, é solução para a outra. Por isso, para encontrar os valores de x que possam satisfazer as duas inequações ao mesmo tempo, vocês precisarão fazer a intersecção entre as duas soluções. Quem nunca ouviu falar sobre essa operação, pode dar uma olhada no texto Operações com Intervalos antes de continuar a leitura.
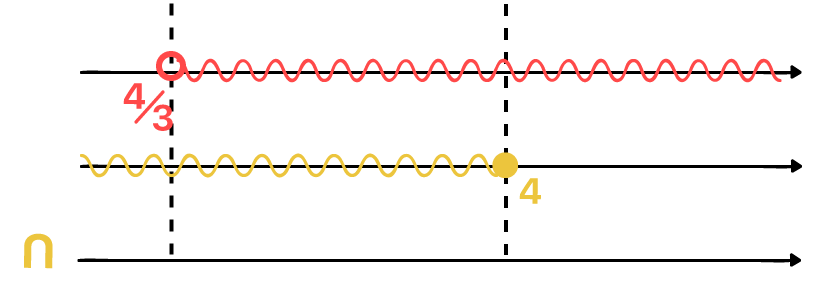
A melhor forma de realizar a intersecção entre duas soluções, é desenhando a representação geométrica de cada uma delas, uma embaixo da outra, e logo abaixo, outra reta real que representará a solução geral para o caso. Traçar pontilhados verticais na região de cada bolinha que representa os valores de referência dos intervalos formados, é algo que pode ajudar na visualização do resultado.
Dados dois conjuntos A e B, chama-se intersecção de A e B o conjunto formado pelos elementos que pertencem a A e a B.
A intersecção entre dois conjuntos, dois intervalos, ou duas soluções, sempre será dada pelos valores reais que pertencem a ambos os conjuntos, intervalos, ou soluções simultaneamente. Não basta que um valor pertença apenas a uma das soluções: para que faça parte do conjunto intersecção, ele deve ser comum a todas as soluções.
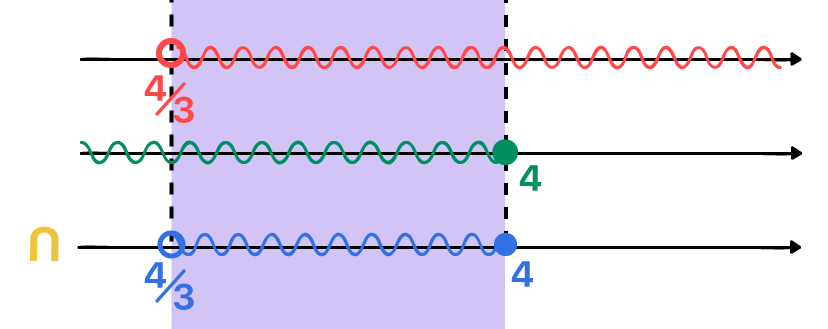
Desta forma, podemos ver na imagem acima, que os únicos valores comuns a ambas as soluções são aqueles que começam em 4/3, sem inclui-lo, já que ele não faz parte da primeira solução (intervalo aberto), e terminam em 4, o incluindo, já que este sim faz parte de ambas as soluções (intervalo fechado). Em forma de conjunto, podemos expressar a solução para as inequações simultâneas que acabamos de resolver da seguinte maneira:
S = {x ∈ ℝ | 4/3 < x ≤ 4}
E agora, para provar que não estou mentindo, vamos fazer um último teste: substituiremos a incógnita x de ambas as inequações que avaliamos por um valor que se situe entre 4/3 e 4. Se a nossa conclusão estiver certa, as duas inequações serão satisfeitas.
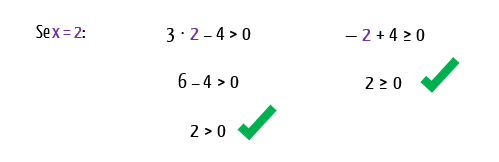
Beleza, pessoal? Utilizaremos esse mesmo método para resolver mais alguns exemplos. Acompanhem comigo!
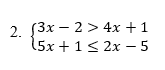
O fato de as duas inequações deste exemplo possuírem a incógnita x de ambos os lados da desigualdade, não altera em nada o método que utilizamos anteriormente. Resolveremos as duas separadamente, e na sequência, faremos a intersecção das duas soluções encontradas.
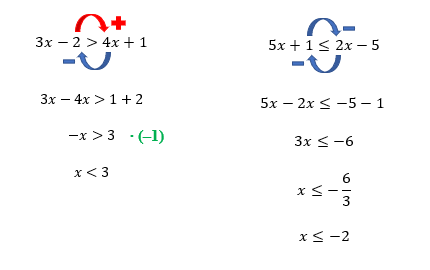
Reparem que temos utilizado bastante a multiplicação por –1 na resolução de algumas das inequações. Pessoal, isso sempre irá acontecer quando a incógnita x estiver negativa, sempre! Assim, devido a importância desse passo na resolução de qualquer inequação, eu sugiro que vocês deem uma olhada no texto Introdução à Inequação do 1º Grau, para obter mais informações sobre como e por que isso acontece.

Para a primeira inequação, 3x – 2 > 4x + 1, qualquer valor menor que –3 poderá substituir o lugar de x e satisfazer a desigualdade. Já para a segunda inequação, 5x + 1 ≤ 2x – 5, qualquer valor menor ou igual a –2 poderá substituir o lugar de x e satisfazer a desigualdade. Mas através da imagem acima, podemos perceber que são comuns a ambas as soluções apenas os valores reais menores do que –3, sem incluí-lo, afinal, –3 não faz parte da primeira solução, e só participam do conjunto intersecção, os valores reais que pertencem a ambas as soluções, não é mesmo?
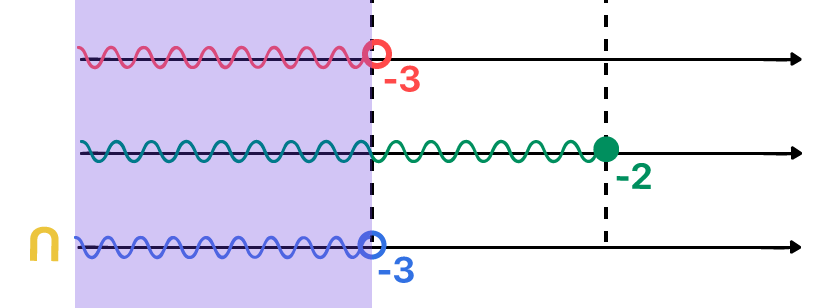
S = {x ∈ ℝ | x < –3}
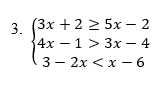
Esse novo exemplo não parece assustador? Pois é, pela primeira vez, nos deparamos com 3 inequações dispostas na forma de um sistema. Mas acreditem, não há problema algum quanto a isso! Vamos resolver as 3 inequações separadamente e depois realizaremos a intersecção das 3 soluções encontradas, ao invés de fazermos tudo isso apenas 2 vezes. Acompanhem comigo!
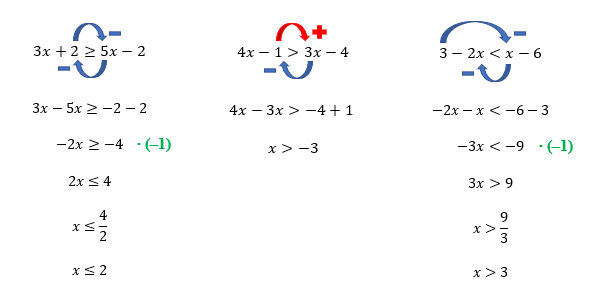
Olhem só que interessante: para a primeira inequação, 3x + 2 ≥ 5x – 2, qualquer valor menor ou igual a 2 poderá substituir o lugar de x e satisfazer a desigualdade. Já para a segunda inequação, 4x – 1 ≥ 3x – 4, qualquer valor maior que –3 poderá substituir o lugar de x e satisfazer a desigualdade. Mas para a terceira e última inequação, 3 – 2x < x – 6, apenas os valores maiores que 3 poderão substituir o lugar de x e satisfazer a desigualdade. Será que em meio a tantas soluções, haverá algum trecho de valores reais que seja comum a todas elas? É isso que nós veremos agora.
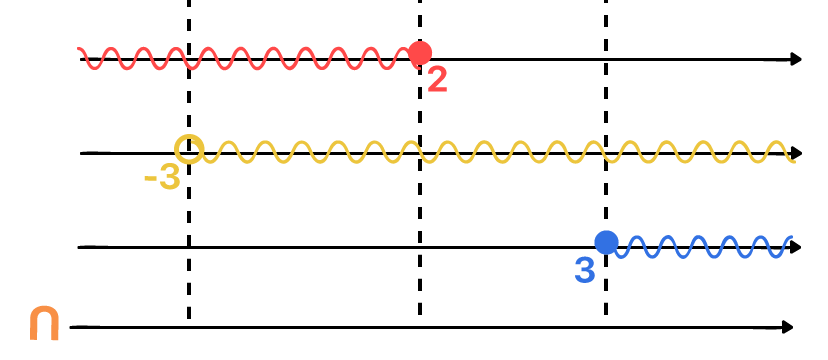
Ficou difícil, não é mesmo? Se nós repararmos na imagem acima com atenção, percebemos que até existe um trecho comum entre a primeira e a segunda solução, e outro trecho comum entre a segunda e a terceira solução, mas nenhum trecho é comum a todas as soluções simultaneamente. Casos como esse podem surgir com toda a certeza, e quando eles acontecem, nós dizemos que a solução é o conjunto vazio.
S = { } = ∅
![]()
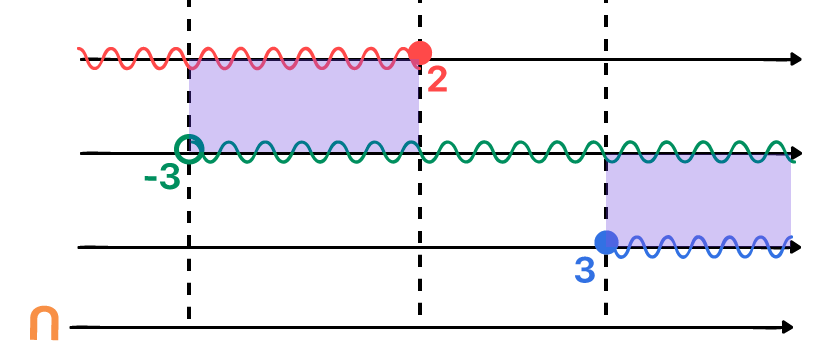
Mas que coisa maluca: ao invés de um sistema, surgiram agora dois sinais de desigualdade em uma mesma inequação! Novamente, não há motivos para se assustar: sempre que as inequações simultâneas se apresentarem dessa forma, vocês deverão separá-las em duas, e assim poderão montar um sistema igualzinho ao dos casos anteriores, o que tornará possível a utilização do mesmo método de resolução que temos aplicado até então.
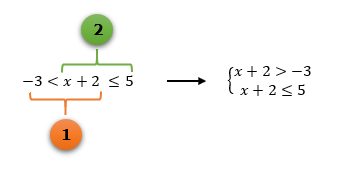
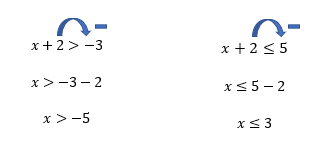
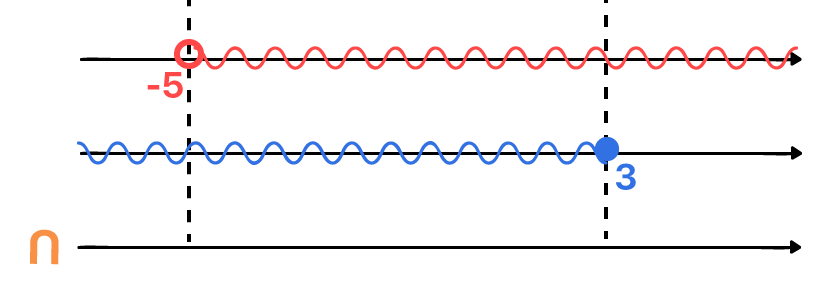
Quem já está craque na intersecção, deve ter percebido, antes mesmo de realizarmos a representação da imagem acima, que os únicos valores reais que podem substituir o lugar do x de ambas as inequações, de forma a satisfazer as duas desigualdades, são aqueles que se situam entre –5, sem incluí-lo, e 3, o incluindo na solução.

S = {x ∈ ℝ | –5 < x ≤ 3}
![]()
E para finalizarmos bem o nosso texto, vamos a um último exemplo! Esse caso é muito semelhante ao anterior, e por isso, seguiremos exatamente os mesmos passos para resolvê-lo. Vem comigo aqui!
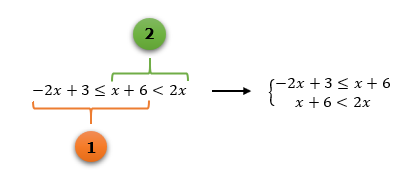
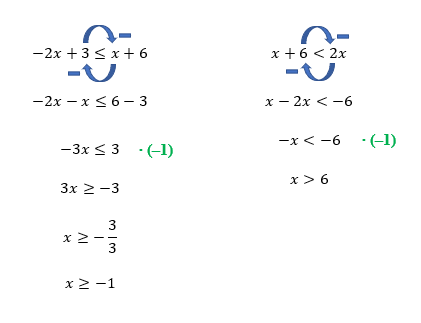
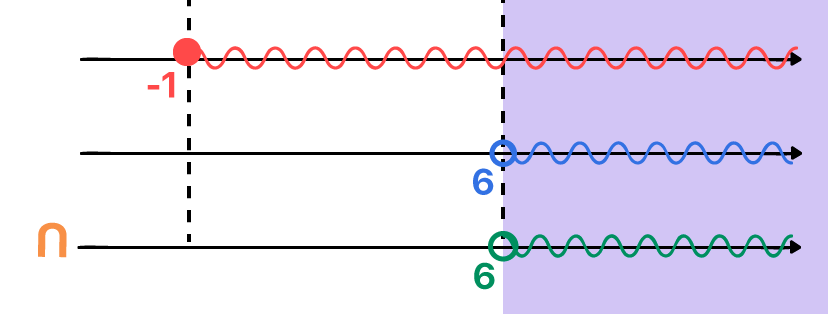
Como vemos na imagem acima, os únicos valores reais que podem substituir o lugar de x em ambas as inequações e satisfazer as duas desigualdades simultaneamente, são aqueles maiores do que 6, o excluindo, já que 6 não faz parte da segunda solução.
S = {x ∈ ℝ | x > 6}
Feito, pessoal? Então já podemos encerrar este texto! Espero que vocês tenham gostado da abordagem, e que possam utilizar os exemplos que vimos como base para resolver situações semelhantes! Eu, se fosse vocês, não deixava de dar uma olhadinha no vídeo que está em anexo! Nele, vocês encontram uma super dica que pode facilitar a resolução de inequações simultâneas semelhantes a que desenvolvemos no exemplo 4!
Um abração! Bons estudos em matemática a todos!
