QUADRADO
13/09/2019
O quadrado é um quadrilátero que possui os 4 lados e os 4 ângulos internos iguais. Por esse motivo, diz-se que ele é um paralelogramo um pouco losango e um pouco retângulo.
Olá, pessoal! Como vão?
Por um acaso vocês já ouviram falar de uma figura geométrica plana que é um pouco retângulo e um pouco losango? Sim, essa figura existe, e é conhecida como quadrado!
Nesse texto, primeiramente, nós vamos conhecer as propriedades do quadrado. Em seguida, vamos descobrir como calcular a sua área e o comprimento de sua diagonal. Além disso, estudaremos as medidas dos raios das circunferências inscrita e circunscrita sobre esta figura geométrica. Posteriormente, ainda sobra espaço para fechar com chave de ouro o estudo dos paralelogramos, e falar um pouco das relações entre o retângulo, o losango e claro, a estrela do texto de hoje!
Ufa, quanta coisa! Mas não se preocupem pessoal, cada um destes conceitos será abordado de forma simples e prática! Agora, está na hora de apresentar a vocês a figura que os trouxe até aqui. Vamos iniciar nossos estudos conhecendo cada uma de suas propriedades. Venham comigo!

1. PROPRIEDADES DO QUADRADO

A partir de agora, nós estudaremos as 9 propriedades que pertencem ao quadrado. Dentre estas, 4 são comuns a todos os paralelogramos. Por isso, é possível dizer que todo quadrado é um paralelogramo. Mas o mais curioso de tudo, é que das 5 propriedades restantes, 3 também pertencem ao losango, e as últimas 2 também pertencem ao retângulo. Isso explica por que nos referimos ao quadrado como meio losango e meio retângulo no início do texto!
1.1 Em todo quadrado, os dois lados opostos são sempre paralelos e congruentes
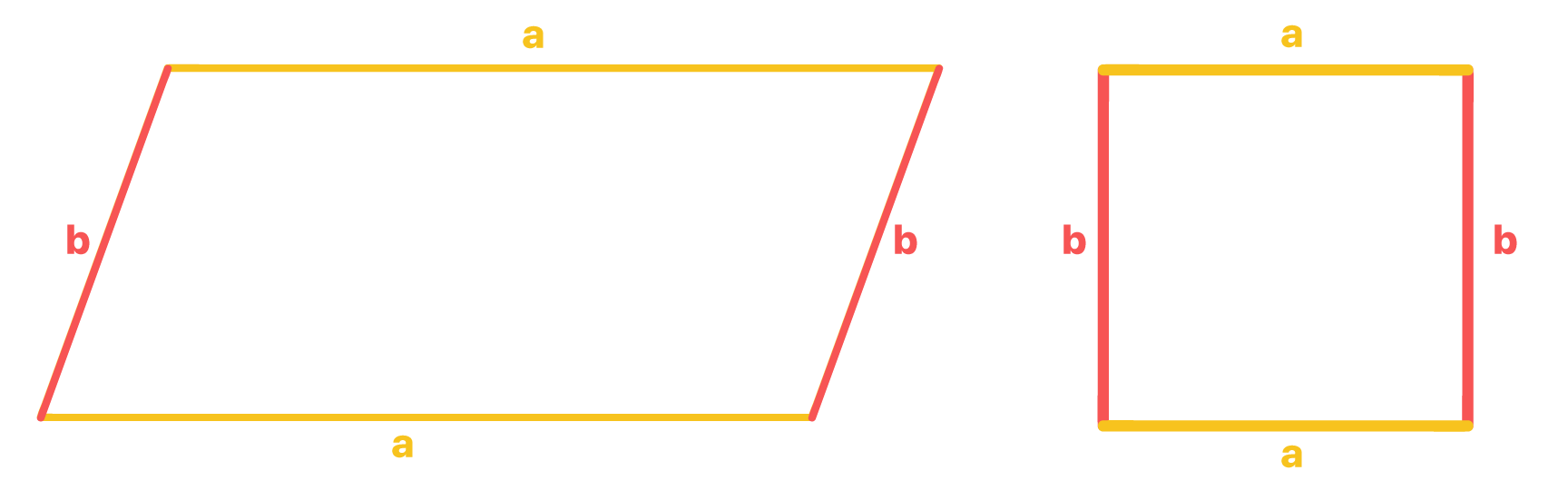
Os dois lados opostos de qualquer paralelogramo são sempre paralelos e de mesma medida. É daí que vem o nome!
1.2 Todo quadrado possui os quatro lados congruentes
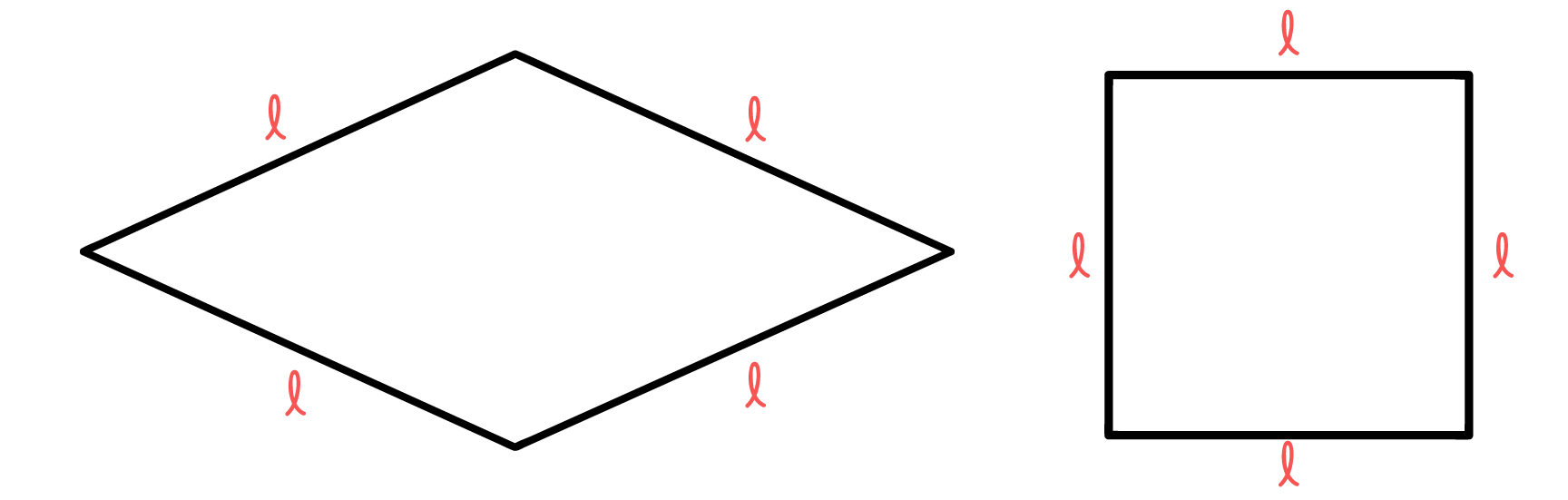
Assim como os losangos, os quadrados também possuem os quatro lados de mesma medida, a qual representamos aqui por l.
1.3 Todos os quatro ângulos dos quadrados são retos

Todos os quatro ângulos dos retângulos e dos quadrados medem 90º.
1.4 Em todo quadrado, os dois ângulos opostos são sempre congruentes
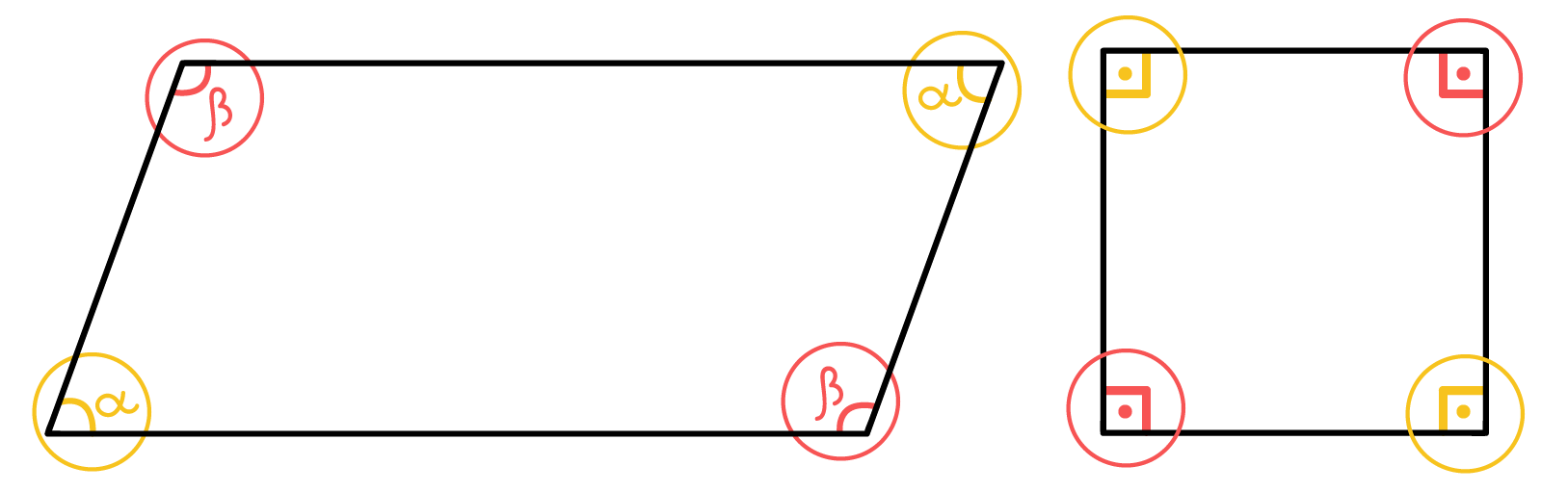
Os dois ângulos opostos de qualquer paralelogramo, e, portanto, de qualquer retângulo, losango ou quadrado, possuem sempre a mesma medida.
1.5 Em todo quadrado, dois ângulos consecutivos são sempre suplementares
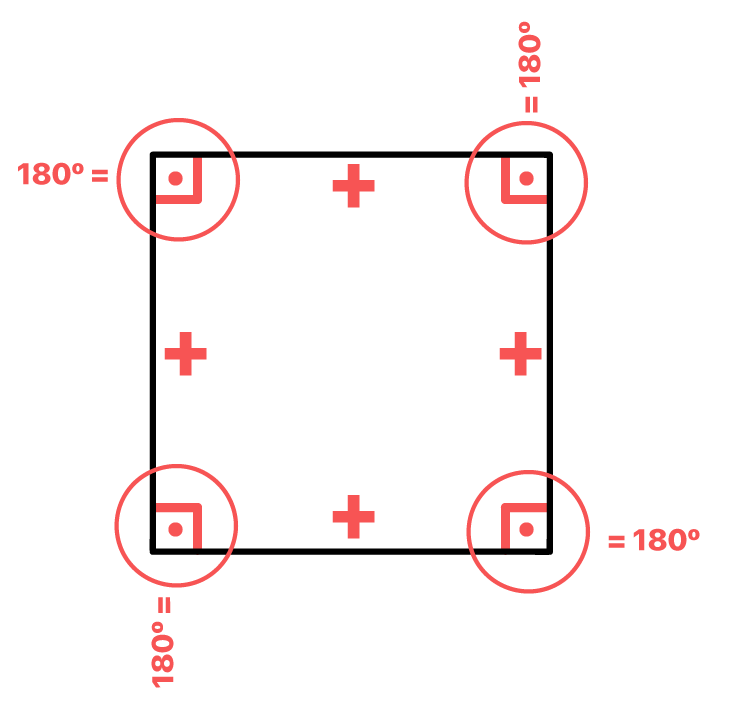
Dois ângulos são suplementares, se a soma de seus valores resultar em 180º. Em qualquer paralelogramo, e, portanto, nos retângulos, losangos e quadrados, a soma dos dois ângulos consecutivos resulta em 180º. Mas o mais interessante é que no quadrado essa propriedade fica ainda mais evidente. Isso porque todos os seus ângulos internos medem 90º!
90º + 90º = 180º
1.6 As diagonais dos quadrados são bissetrizes dos seus vértices
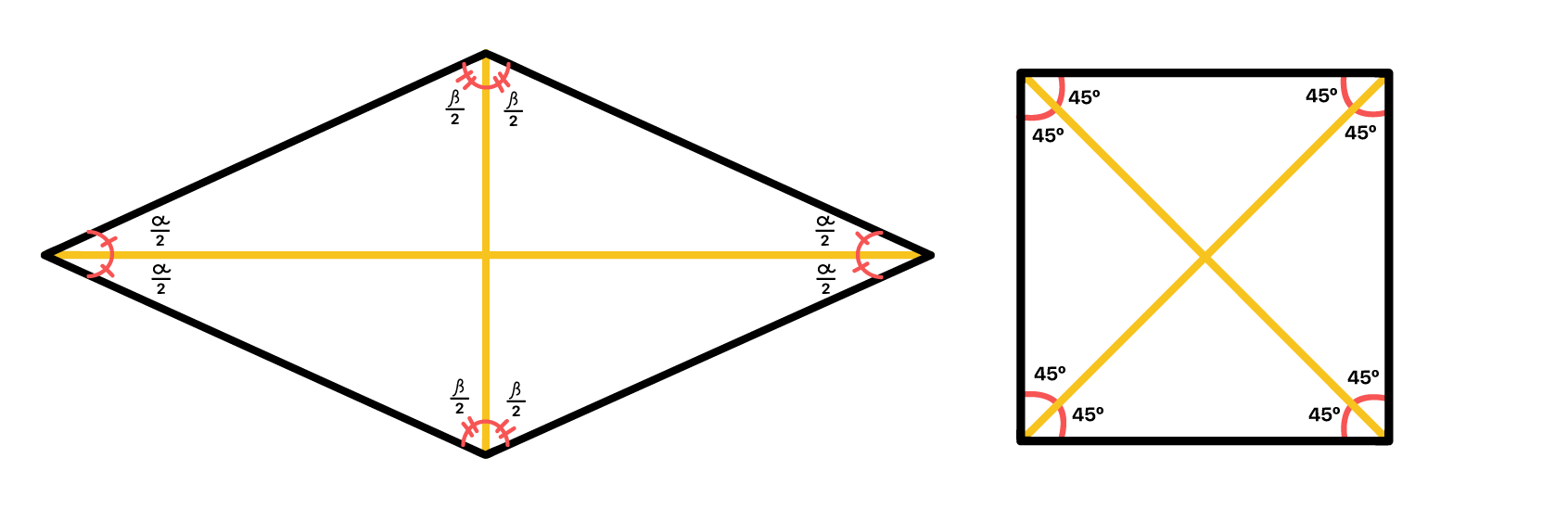
Uma bissetriz é uma reta que divide um ângulo em duas partes iguais. Observando a imagem acima, podemos perceber que tanto as diagonais do losango, quanto as do quadrado são bissetrizes de seus vértices.
Mas o quadrado tem uma vantagem nessa propriedade! Vejam que no caso do losango, os ângulos internos não são definidos. Por isso, são descritos como α e β, de forma que cada diagonal gera quatro ângulos iguais de medida α/2 e β/2. Felizmente, quando se trata de um quadrado, os valores dos ângulos internos são conhecidos, e o melhor, são todos iguais, medem 90º. Desta forma, cada diagonal do quadrado divide dois ângulos de 90º pela metade, gerando assim, quatro ângulos de 45º.
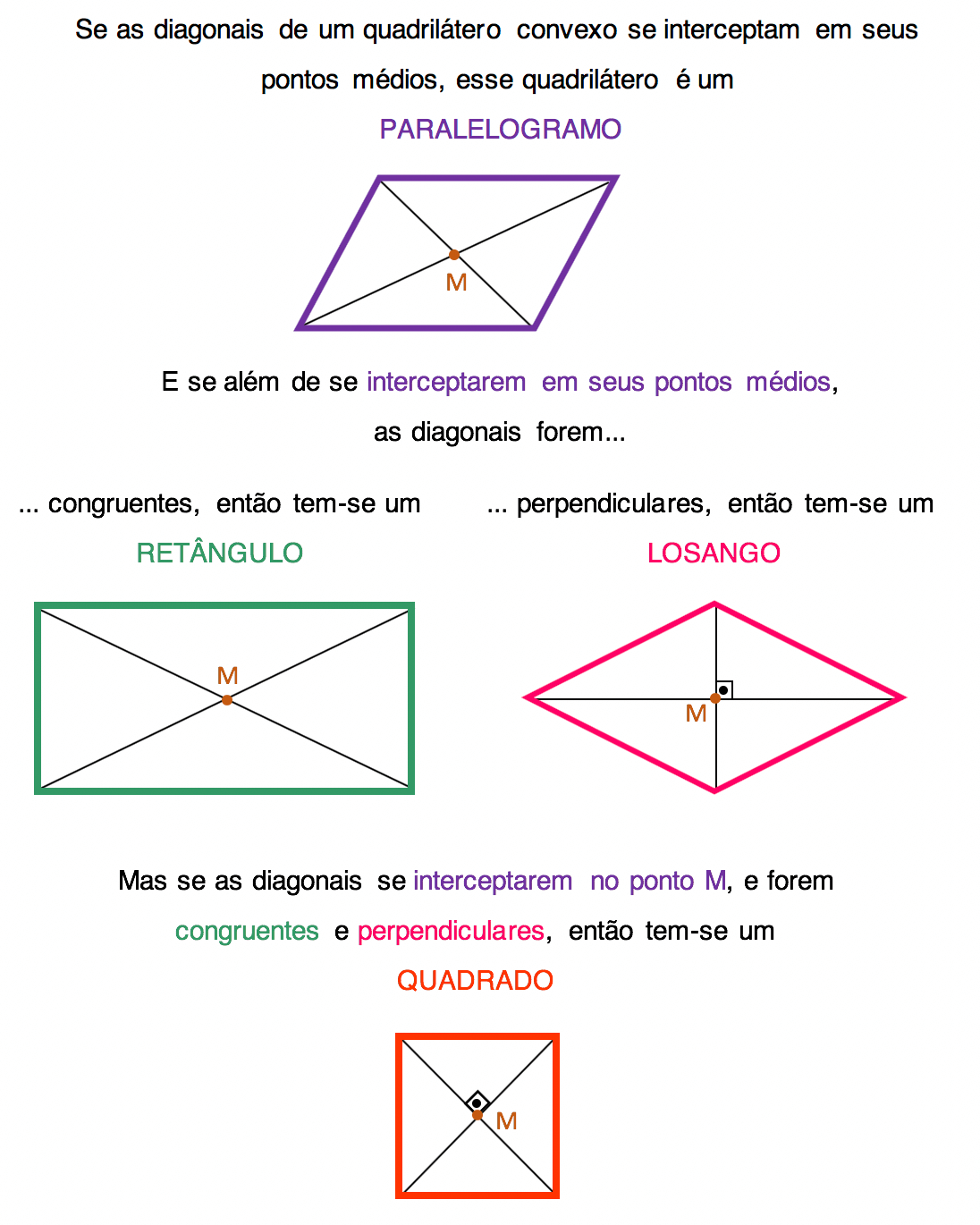
1.7 Em todo quadrado, as diagonais interceptam-se nos seus pontos médios
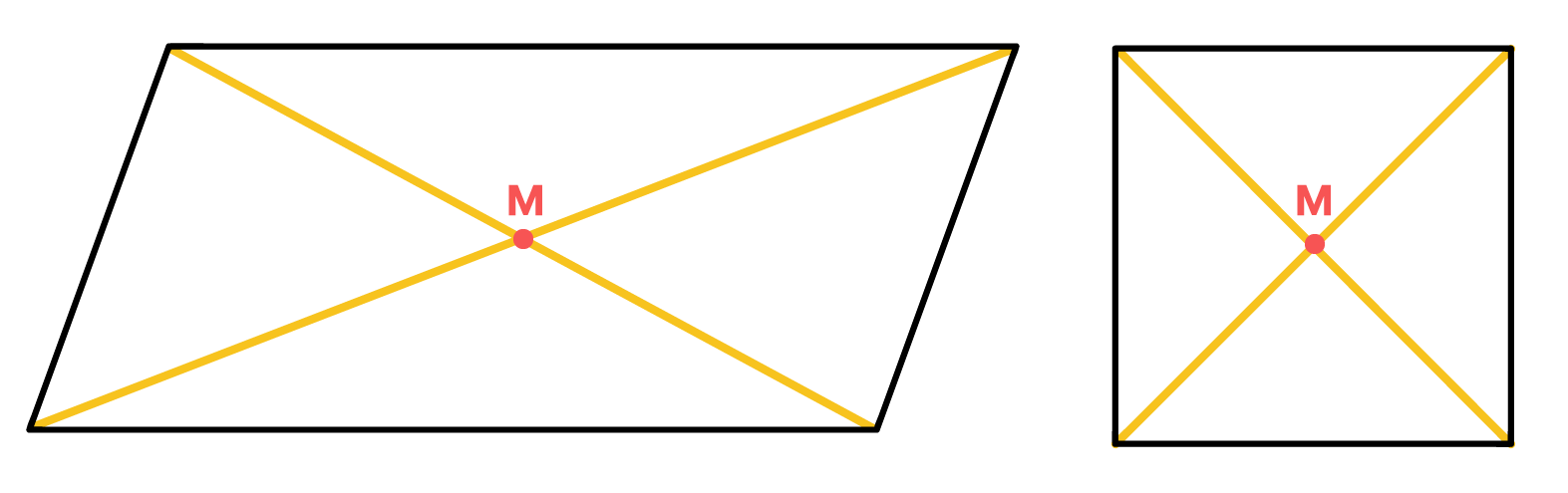
As diagonais de todo paralelogramo, e, portanto, de todos os retângulos, losangos e quadrados cortam-se exatamente em seus respectivos pontos médios. Isso significa que em todas essas figuras geométricas, o ponto M em que as diagonais se encontram divide o comprimento das mesmas pela metade.
1.8 As diagonais dos quadrados são perpendiculares entre si
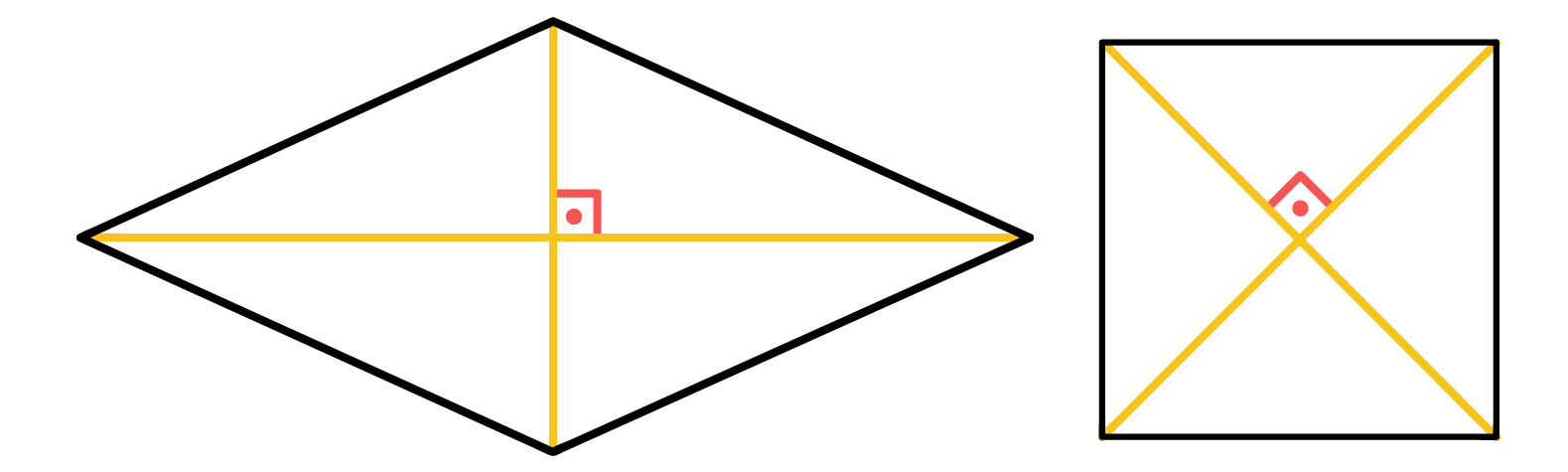
Tanto as diagonais do losango quanto as diagonais do quadrado são perpendiculares entre si. Isso significa que quando estas diagonais se intersectam, elas formam um ângulo de 90º entre si. Mas o melhor de tudo ainda está por vir, pessoal. Por formar um ângulo de 90º entre si, as diagonais dos losangos e quadrados os dividem em quatro triângulos retângulos iguais.
1.9 As diagonais dos quadrados são congruentes
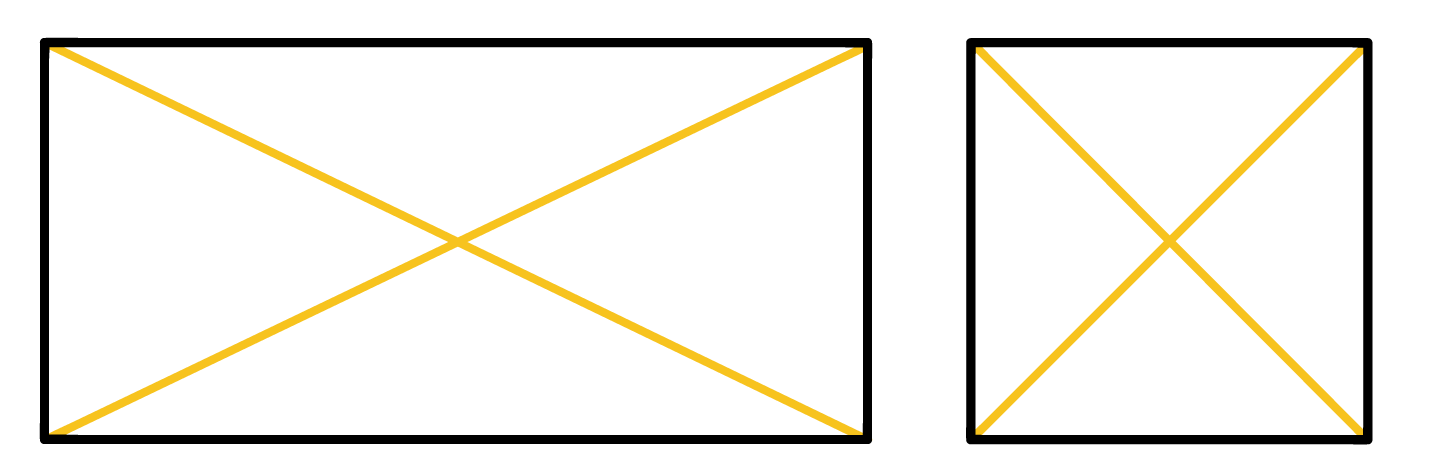
Tanto as diagonais dos retângulos quanto as diagonais dos quadrados possuem o mesmo comprimento.
Legal, não é, pessoal? Neste momento, nós já conhecemos uma série de informações sobre o quadrado. Agora, vamos aprender algumas fórmulas que também são muito importantes para o estudo dessa figura geométrica. Sigam comigo!
2. FÓRMULA DA ÁREA DO QUADRADO
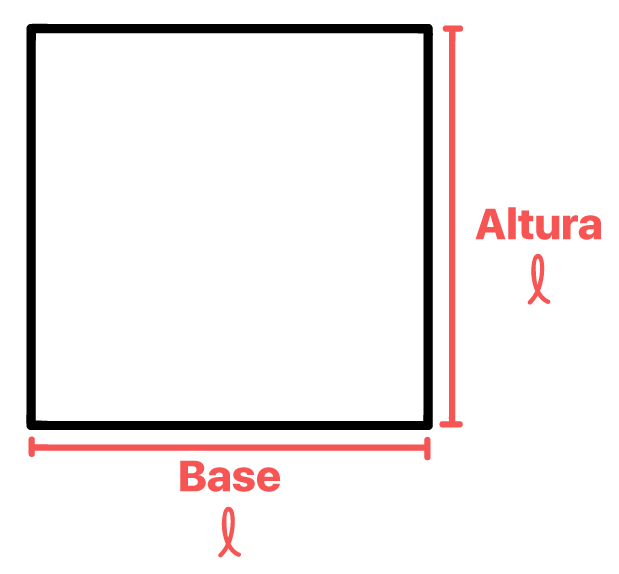
A fórmula da área do quadrado é muito simples, pessoal! Sabe-se que todo quadrado é um retângulo, e que a área do retângulo pode ser calculada através do produto da medida de sua base pela medida de sua altura. Portanto, nós podemos utilizar essa mesma fórmula para encontrar a área do quadrado!
Mas calma, pessoal, ainda não desvendamos a melhor parte! Nós vimos em uma das propriedades do quadrado, que todos os seus 4 lados possuem a mesma medida, representada neste texto por l. Isso significa que as medidas da base e da altura do quadrado valem l, de tal forma que:
A = b ⨯ h
A = l ⨯ l
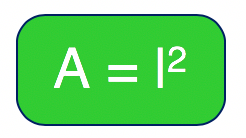
Para memorizar a fórmula da área do quadrado, vocês podem lembrar da seguinte frase:
A área do quadrado é lado vezes lado.
3. FÓRMULA PARA ENCONTRAR A MEDIDA DA DIAGONAL DO QUADRADO
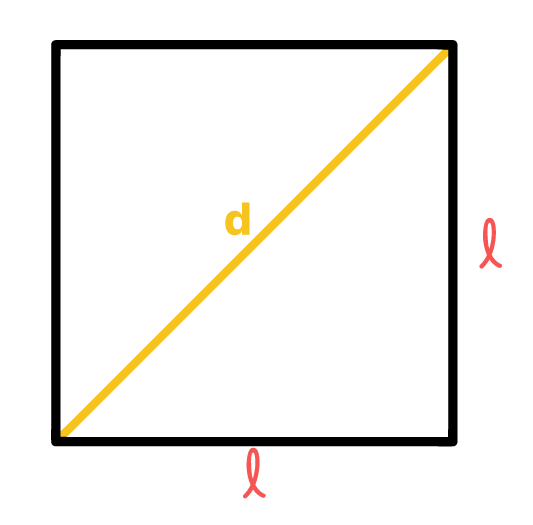
Através das propriedades vistas logo no início do texto, nós descobrimos que a diagonal do quadrado o divide em dois triângulos retângulos iguais. Esse conhecimento é de extrema importância para determinarmos a fórmula da medida da diagonal do quadrado. Isso porque quando se fala em triângulo retângulo, temos a disposição o Teorema de Pitágoras!
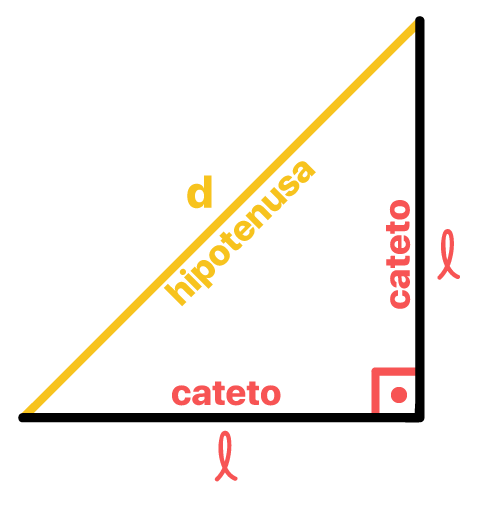
Segundo o Teorema de Pitágoras, em um triângulo retângulo, a medida da hipotenusa elevada ao quadrado é igual a soma dos quadrados das medidas dos catetos. Sabe-se no nosso caso, que os catetos do triângulo formado têm o mesmo comprimento que os lados do quadrado, e que a hipotenusa do triângulo é a própria diagonal do quadrado. Dessa forma, pode-se concluir que:
d2 = l2 + l2
d2 = 2·l2
d = √(2l2)
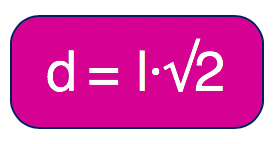
Assim, o comprimento da diagonal de qualquer quadrado pode ser dado pelo produto entre a medida do seu lado e raiz quadrada de 2.
4. RAIO (r) DA CIRCUNFERÊNCIA INSCRITA

Uma circunferência está inscrita em um quadrado, quando ela se encontra dentro deste quadrado. Dessa forma, a sua borda tangencia todos lados do quadrado, como vemos na imagem acima. O raio dessa circunferência costuma ser definido como a distância entre centro e qualquer ponto de sua borda. Mas aqui, nós vamos traçá-lo propositalmente do centro até um dos pontos de sua borda que está em contato com o lado do quadrado. Assim, chegamos a seguinte situação:
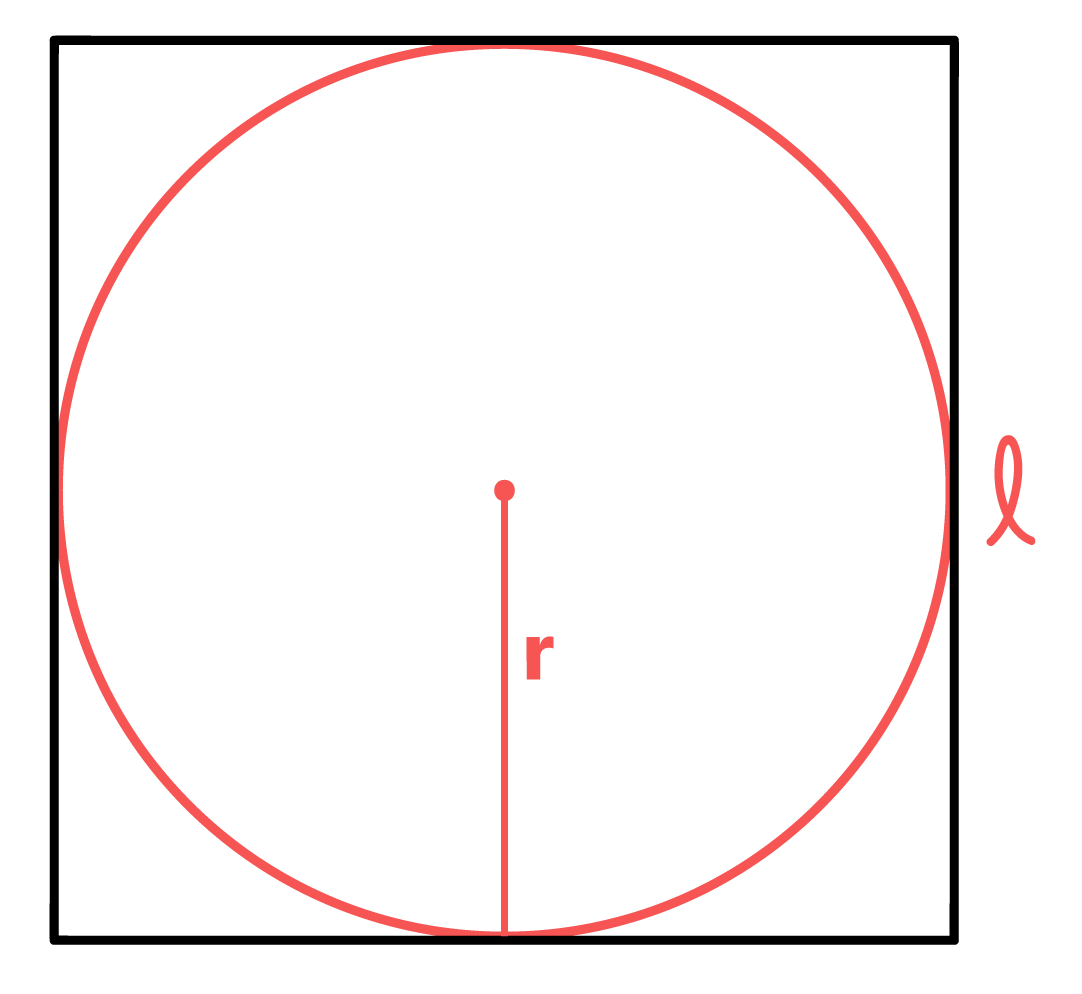
A imagem acima não deixa dúvidas de que o raio da circunferência inscrita no quadrado, que representamos por r, possui exatamente a metade do comprimento do lado l do quadrado.

Mas as surpresas não terminam por aí, pessoal. O raio da circunferência inscrita no quadrado também representa a distância entre centro do quadrado e o ponto médio de um de seus lados. Só que essa é justamente a definição do apótema do quadrado. Por isso, o apótema de um quadrado (ap) é exatamente igual ao raio da circunferência inscrita sobre ele, e portanto, também equivale a metade do comprimento do lado do quadrado.

5. RAIO (R) DA CIRCUNFERÊNCIA CIRCUNSCRITA

Uma circunferência é circunscrita a um quadrado, quando ela se encontra fora deste quadrado. Dessa forma, a sua borda tangencia todos os vértices do quadrado, como vemos na imagem acima. O raio dessa circunferência também pode ser definido como a distância entre centro e um ponto qualquer de sua borda. Mas novamente, nós vamos traçá-lo estrategicamente do centro até um dos pontos em que sua borda tangencia um dos vértices do quadrado. Assim, chegamos a seguinte situação:

E aí, isso fez algum sentido para vocês? Calma, tenho certeza que ao traçarmos novamente o raio da circunferência do centro até o vértice oposto daquele que havíamos traçado, vocês vão lembrar de um elemento que acabamos de estudar. Observem a imagem abaixo.

Pois é, o diâmetro da circunferência circunscrita é exatamente igual a diagonal do quadrado! Por isso, podemos dizer que o raio da circunferência circunscrita ao quadrado, que representamos por R, corresponde exatamente a metade do comprimento da diagonal do quadrado.

Bom, sabe-se que o comprimento da diagonal do quadrado é dado pelo produto da medida do seu lado por raiz quadrada de 2. Dessa forma, também é possível obter o raio da circunferência circunscrita do quadrado em função da medida do seu lado l.
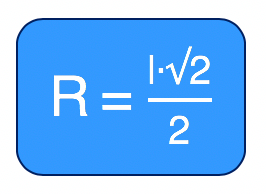
Entendido, pessoal? Agora que já conhecemos todo o formulário do quadrado, é hora de fazermos um estudo teórico bem importante! Esse estudo vai fechar com chave de ouro o aprendizado de vocês a respeito dos paralelogramos. Me acompanhem!
6. RELAÇÃO ENTRE OS PARALELOGRAMOS
A partir das informações dadas acima, não há dúvidas de que se formássemos conjuntos aos quais pertencessem todos os paralelogramos, retângulos, losangos e quadrados, a sua representação na forma de diagrama seria a seguinte:
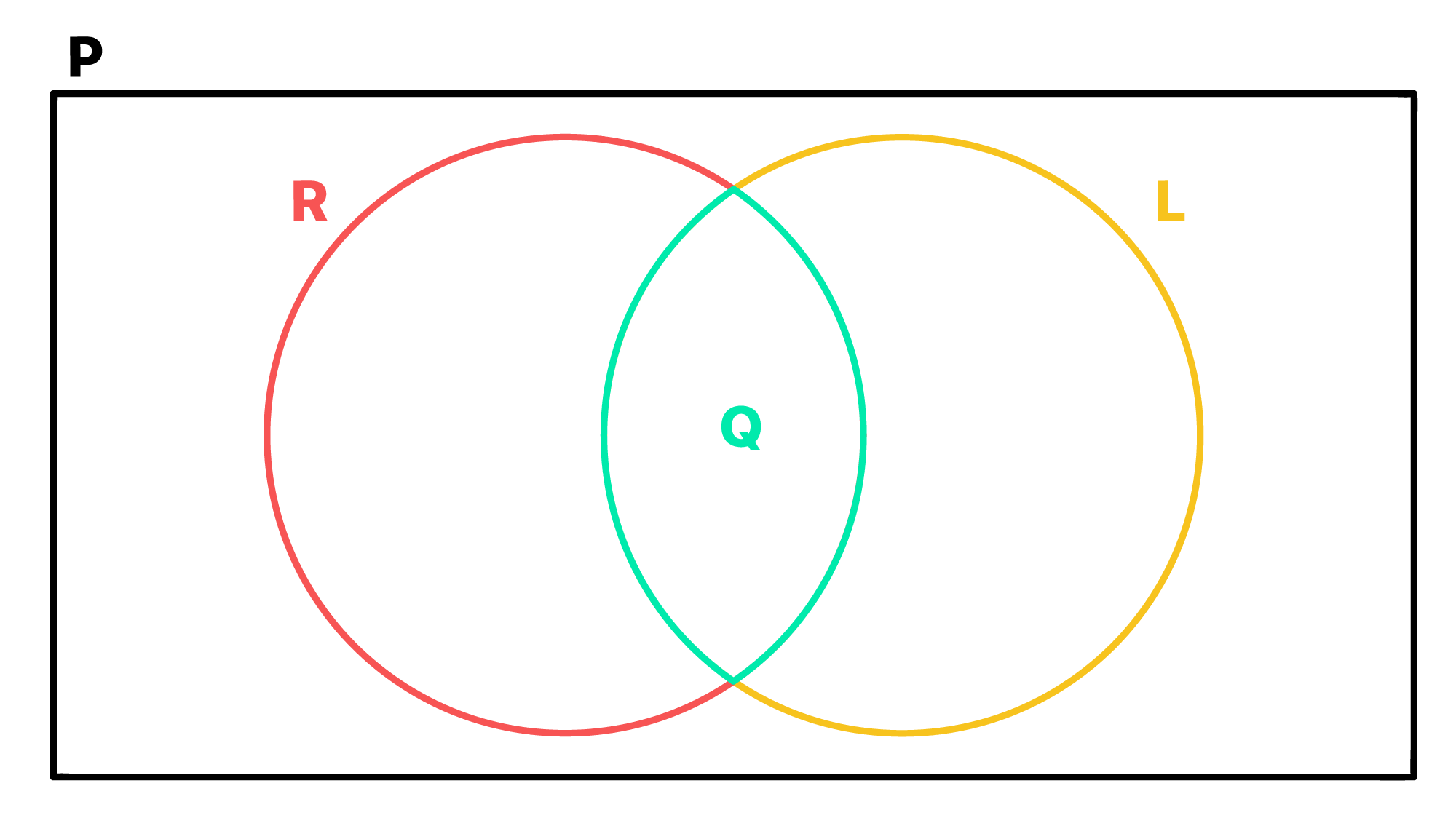
Prestem bastante atenção nesse diagrama, e assim vocês nunca esquecerão que todo quadrado é um retângulo e um losango, e que por sua vez, todo retângulo, quadrado, ou losango, será sempre um paralelogramo.
E lá se foi mais um texto sobre geometria plana! Espero que todos os conceitos apresentados aqui tenham contribuído para os estudos de vocês, afinal, esse é o objetivo! Quem quiser testar todo o conhecimento que adquiriu, pode ficar à vontade para dar uma olhada no vídeo que está em anexo. Vamos resolver juntos alguns exercícios muito curiosos, que como sempre, abrangem diversas definições da matemática.
Ahh.. E se você curtiu esse texto, aproveite também para conhecer a plataforma do Professor Ferretto. Clique aqui para saber como a plataforma funciona!
Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!
Um abração a todos e até o próximo texto!