Por mais estranho que possa parecer, a verdade é que as palavras circunferência e círculo não denominam a mesma figura geométrica. A circunferência é uma linha curva, fechada, cujos pontos são todos equidistantes de um mesmo ponto fixo, o centro. Enquanto isso, o círculo é definido como uma superfície plana limitada por uma circunferência.

Olá, pessoal! Tudo certo por aí?

Vocês sabiam que os termos “circunferência” e “círculo” não representam a mesma figura geométrica? Exatamente, existe uma diferença crucial entre eles, que é base para o nosso estudo de hoje! Depois de entendê-la, vamos conhecer as fórmulas que nos permitem obter comprimento da circunferência e a área do círculo, e então finalizaremos o texto resolvendo um exercício do ENEM, para que vocês fiquem preparados para prestar essa prova logo mais!

Entendido, pessoal? Imagino que vocês estejam curiosos para entender melhor qual é a diferença entre a circunferência e o círculo. Agora é hora de desvendar este mistério. Vem comigo!

1. A DIFERENÇA ENTRE CIRCUNFERÊNCIA E CÍRCULO

A circunferência é uma linha fechada, em que qualquer um de seus pontos possui a mesma distância do ponto central.

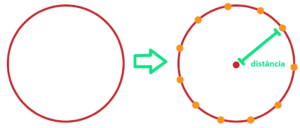
Para não esquecer do significado de circunferência, vocês podem associá-la, por exemplo, ao formato de um anel, ou de uma aliança.

Agora, e se vocês resolvessem preencher uma circunferência, ocupando todos os pontos do seu interior, será que ela ainda poderia ser chamada assim? Pois bem, uma circunferência preenchida é conhecida como círculo.

O círculo é uma superfície plana limitada por uma circunferência. Existe uma peça de metal muito conhecida e utilizada cujo formato é justamente o de um círculo, ou disco. Para lembrar do significado de um círculo, vocês podem associá-lo a uma moeda!

Então, pessoal, basicamente, quando falamos em circunferência, nos referimos a uma linha fechada que possui uma única dimensão. Por isso, é possível calcular apenas o comprimento da circunferência. Contudo, quando se fala em círculo, tem-se em vista uma superfície que possui duas dimensões. Dessa forma, é possível calcular a área do círculo. Quem seguir comigo, vai descobrir tudo sobre essas duas fórmulas famosas. Vamos lá!

2. FÓRMULA DO COMPRIMENTO DA CIRCUNFERÊNCIA

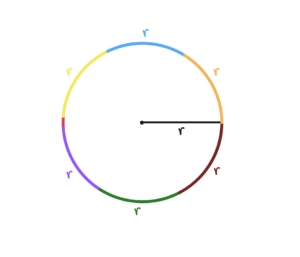
A fórmula do comprimento da circunferência é composta simplesmente pelo produto entre 2, o número irracional 𝛑 e a medida do raio r da circunferência.

De maneira simplificada, pode-se dizer que a fórmula do comprimento da circunferência é dada por C = 2πr, porque a medida do raio de toda circunferência cabe cerca de 6,28 ou 2π vezes em toda a sua extensão.

Querem saber mais sobre essa relação entre o comprimento da circunferência ou o perímetro do círculo e o seu raio r? Então deem uma olhada no vídeo abaixo antes de seguir. Nele, eu também falo sobre o significado de 1 radiano, não deixem de conferir!

3. FÓRMULA DA ÁREA DO CÍRCULO

A fórmula da área do círculo é dada pelo produto entre o número irracional π e o raio r do círculo elevado ao quadrado. A dedução desta fórmula é bastante curiosa e interessante. A imagem abaixo nos conduz ao raciocínio utilizado.

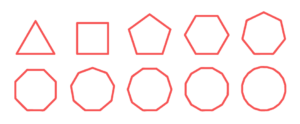
Temos acima uma série de polígonos regulares de 3, 4, 5, 6, 7, 8, 9, 10, 12 e 20 lados. Reparem que na medida em que o número de lados vai aumentando, o formato dos polígonos fica cada vez mais parecido com o formato de um círculo. A partir dessa ideia, é possível demonstrar a fórmula da área do círculo, como mostro no vídeo abaixo. Assistam comigo!

Entendido, pessoal? Então que tal aplicar todos os conceitos que acabamos de estudar e ainda se preparar para a prova do ENEM? Sigam comigo rumo ao próximo item!

4. CAIU NO ENEM!

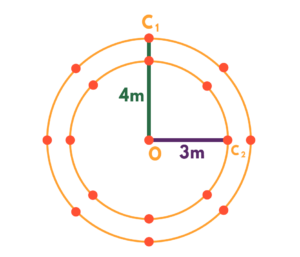
A figura é uma representação simplificada do carrossel de um parque de diversões, visto de cima. Nessa representação, os cavalos estão identificados pelos pontos escuros, e ocupam circunferências de raios 3 m e 4 m, respectivamente, ambas centradas no ponto O. Em cada sessão de funcionamento, o carrossel efetua 10 voltas.

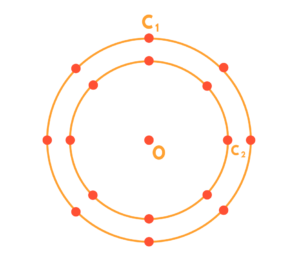
Quantos metros uma criança sentada no cavalo C1 percorrerá a mais do que uma criança no cavalo C2, em uma sessão? Use 3,0 como aproximação para 𝛑.

Segundo o contexto apresentado no enunciado, fica evidente que estamos falando sobre o comprimento de duas circunferências. A mais interna, na qual se encontra o cavalo C2, possui raio de 3m. Já a mais externa, na qual se encontra o cavalo C1, possui raio de 4m. Sabendo que o comprimento de uma circunferência é diretamente proporcional a medida de seu raio, parece lógico que a criança que se sentar no cavalo C1 percorrerá alguns metros a mais do que aquela que se sentar no cavalo C2.

Mas para saber quantos metros a mais serão percorridos pela criança que optar pelo cavalo C1, é preciso determinar as distâncias d₁ e d₂ que ambas as crianças percorrerão. Para isso, basta definir o comprimento das duas circunferências, e multiplicar os valores obtidos por 10, visto que são 10 voltas por sessão de funcionamento. Por fim, é só calcular a diferença entre os resultados obtidos. Olhem só!

d₁ = 10 · 2·π·r₁              d₂ = 10 · 2·π·r₂

d₁ = 10·2·3·4                 d₂ = 10·2·3·3

d₁ = 240 m                     d₂ = 180 m

d₁ – d₂ = 240 – 180 = 60 m

5. QUE TAL COMPLEMENTAR O ASSUNTO?

Bem tranquilo, não é, pessoal? Vejam que esse assunto não tem mistério! Mas se vocês quiserem saber mais sobre ele, não deixem de acompanhar o vídeo que está em anexo logo abaixo. Neste vídeo, eu abordo mais uma série de conceitos que envolvem a circunferência e o círculo e também resolvo alguns exercícios. Espero vocês por lá!

E quem gostou deste texto também não pode perder a oportunidade de conhecer a plataforma do Professor Ferretto! Clique aqui para saber como a plataforma funciona!

Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!

No mais, desejo ótimos estudos a todos! Um grande abraço a até o próximo texto!