O paralelogramo é um quadrilátero cujos lados opostos são paralelos. Estudar as propriedades do paralelogramo significa entender algumas definições sobre as medidas de seus lados, suas diagonais e sobre os seus ângulos internos.

 

Olá, pessoal! Tudo bem?

Os quadriláteros, dentro da geometria plana, são os polígonos que possuem quatro lados. Mas é só a gente parar um pouco para pensar, que logo nos vem a mente uma série de figuras geométricas que possuem 4 lados, não é? Nosso texto de hoje abordará apenas uma delas, o paralelogramo, e também suas propriedades! Além disso, descobriremos juntos como calcular a área de um paralelogramo, um conceito que pode nos ajudar a resolver inúmeras questões do ENEM e dos vestibulares!

Preparados!? Então, sem mais delongas, vamos iniciar o estudo dos paralelogramos. Venham comigo!

 

1. PROPRIEDADES DO PARALELOGRAMO

Para quem não conhece, a figura geométrica apresentada na imagem acima é um paralelogramo! O formato dessa figura é resultante de uma série de propriedades que envolvem as medidas de seus lados, de as suas diagonais e também dos seus ângulos internos. Vamos estudar cada uma dessas propriedades agora mesmo. É só seguir comigo!

 

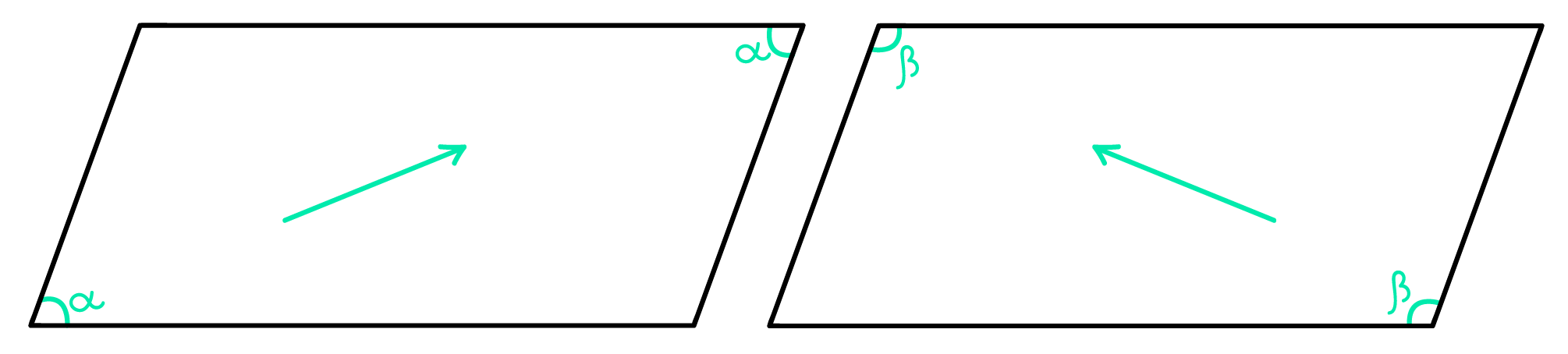
1.1 Em todo paralelogramo, os dois ângulos opostos são sempre congruentes

A primeira propriedade nos mostra que em qualquer paralelogramo, os dois ângulos opostos possuem o mesmo valor. Mas vocês sabem o que são ângulos opostos? A imagem abaixo tentará esclarecer esse detalhe.

 

1.2 Em todo paralelogramo, os dois lados opostos são sempre paralelos e congruentes

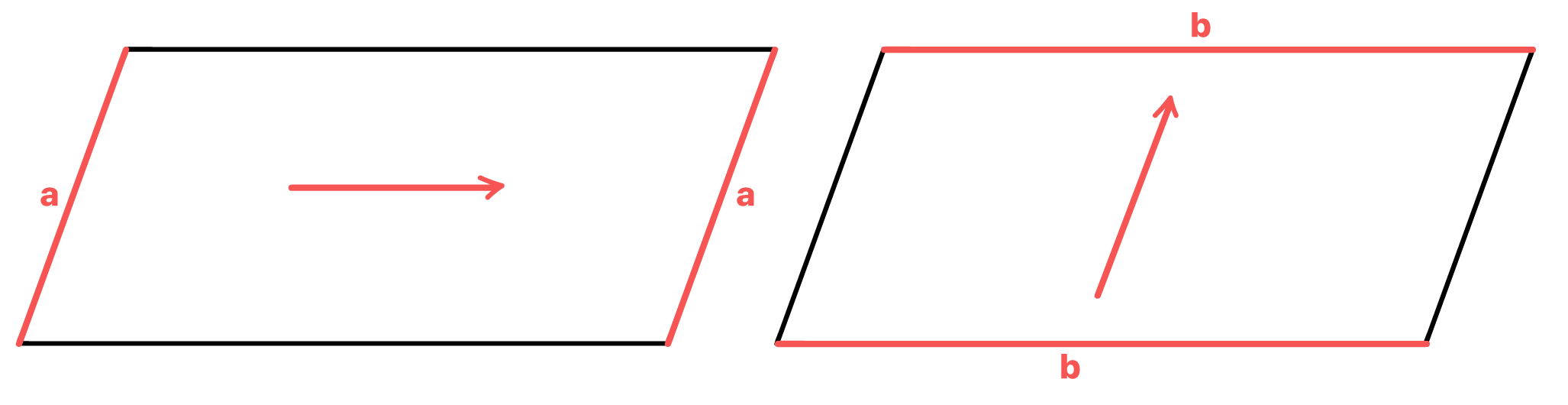
A propriedade anterior nos informou que os dois ângulos opostos do paralelogramo são sempre congruentes, ou seja, possuem a mesma medida. Felizmente, podemos dizer que os lados opostos do paralelogramo também possuem o mesmo comprimento.

Mas para entendermos a segunda propriedade por completo, precisamos conhecer a definição de “paralelo” para a geometria. Dois segmentos distintos são paralelos, quando mantém a mesma distância entre si ao longo de toda a sua extensão, de forma a jamais se cruzar, ou ter algum ponto em comum.

Reparem nos segmentos da figura acima. Eles representam os dois lados opostos de um paralelogramo, só que a título de exemplo, eles foram  levemente aproximados. Se nós os observarmos com atenção, veremos que esses segmentos realmente nunca poderão se encontrar se manterem a mesma distância entre si ao longo de toda a sua extensão. Isso nos mostra que os dois lados opostos do paralelogramo são mesmo paralelos.

 

1.3 Em todo paralelogramo, as diagonais interceptam-se nos seus pontos médios

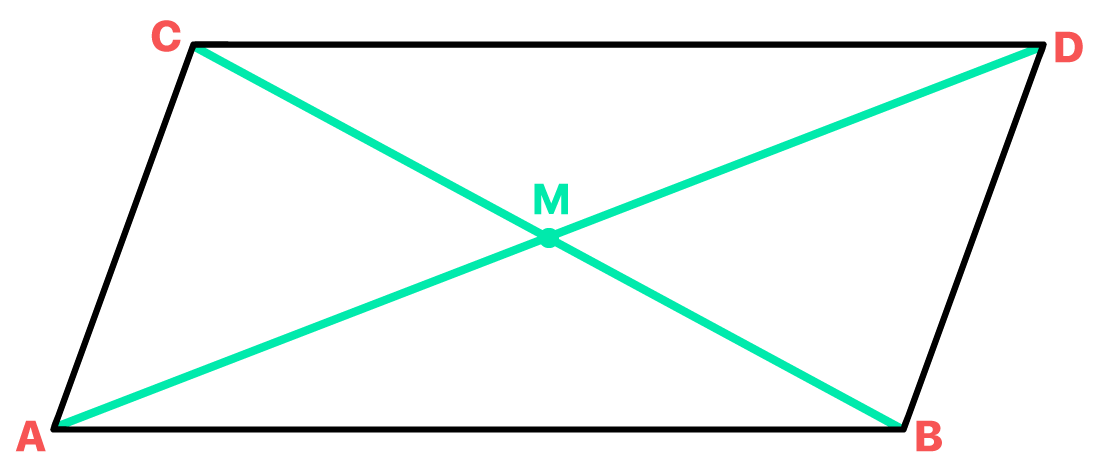
Todo o quadrilátero convexo possui duas diagonais, como as que vemos na imagem acima. Acontece que no paralelogramo, o ponto em que as duas diagonais se encontram, e que chamamos de M, acaba sendo o ponto médio de ambas as diagonais.

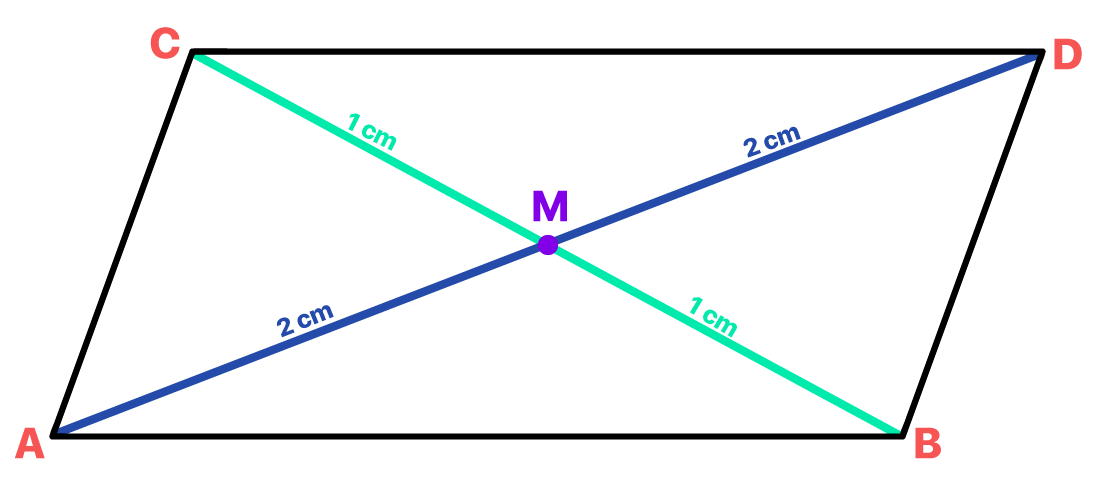
O ponto médio de um segmento sempre irá o dividi-lo pela metade. Por isso, vocês podem ter certeza que a diagonal AD, do paralelogramo acima, mede 4 cm, enquanto que a diagonal BC mede 2 cm.

 

1.4 Em todo paralelogramo, dois ângulos consecutivos são sempre suplementares

Para entendermos a última propriedade dos paralelogramos, vamos relembrar, primeiramente, o que são ângulos suplementares. Dois ângulos α e β são suplementares, se a soma de seus valores resultar em 180º.

α + β = 180º

Agora, vamos ao conceito de ângulos consecutivos. Um ângulo é consecutivo a outro, quando vem depois do outro, ou quando se encontra na sequência do outro. Na imagem abaixo, vejam, se tomarmos por base o ângulo α que se encontra mais a esquerda no paralelogramo, temos que o ângulo que aparece na sequência é o β. Por isso, α e β são consecutivos. Para simplificar, entendam ângulos consecutivos como ângulos “vizinhos”, como também mostra a imagem seguinte.

 

2. APLICANDO AS PROPRIEDADES DO PARALELOGRAMO

Dado o paralelogramo da imagem acima, encontre todos os seus demais ângulos internos.

Pensando na primeira propriedade dos paralelogramos, podemos definir, logo de cara, o ângulo oposto ao ângulo de 30º apresentado na imagem.

Agora, já podemos utilizar a 4ª propriedade dos paralelogramos! Isso porque o ângulo que ainda não conhecemos é o ângulo consecutivo, ou vizinho de 30º. Se consideramos este ângulo como sendo α, encontraremos o valor de β num instante através da relação dos ângulos suplementares, vejam só!

α + β = 180º

30º + β = 180º

β = 180º – 30º

β = 150º

Tranquilo, não é mesmo? Assim, podemos partir para o próximo item do texto. Veremos na sequência, como encontrar a área de um paralelogramo. Sigam comigo!

 

3. ÁREA DE UM PARALELOGRAMO

Para calcular a quantidade de m², cm², km² de uma figura geométrica, ou seja, para calcular a sua área, precisamos conhecer o valor de suas dimensões. No caso do paralelogramo, devemos conhecer o valor de sua base, representada por b, e de sua altura, representada por h.

Vejam na imagem acima, que a altura do paralelogramo é a medida daquele segmento que sai da base b, formando um ângulo de 90º com ela, e vai em direção ao lado oposto do paralelogramo. Nesse sentido, é muito importante não confundir o seguinte detalhe: a medida da altura de um paralelogramo não é igual a medida de um de seus lados!

Conhecendo o comprimento da base e da altura do paralelogramo, é possível definir a sua área através da fórmula:

É verdade que observando o segmento que representa a altura do paralelogramo, poderíamos pensar que a fórmula não condiz com a sua real área. Mas se analisarmos o caso por outro lado, não teremos dúvidas de que a fórmula está correta.

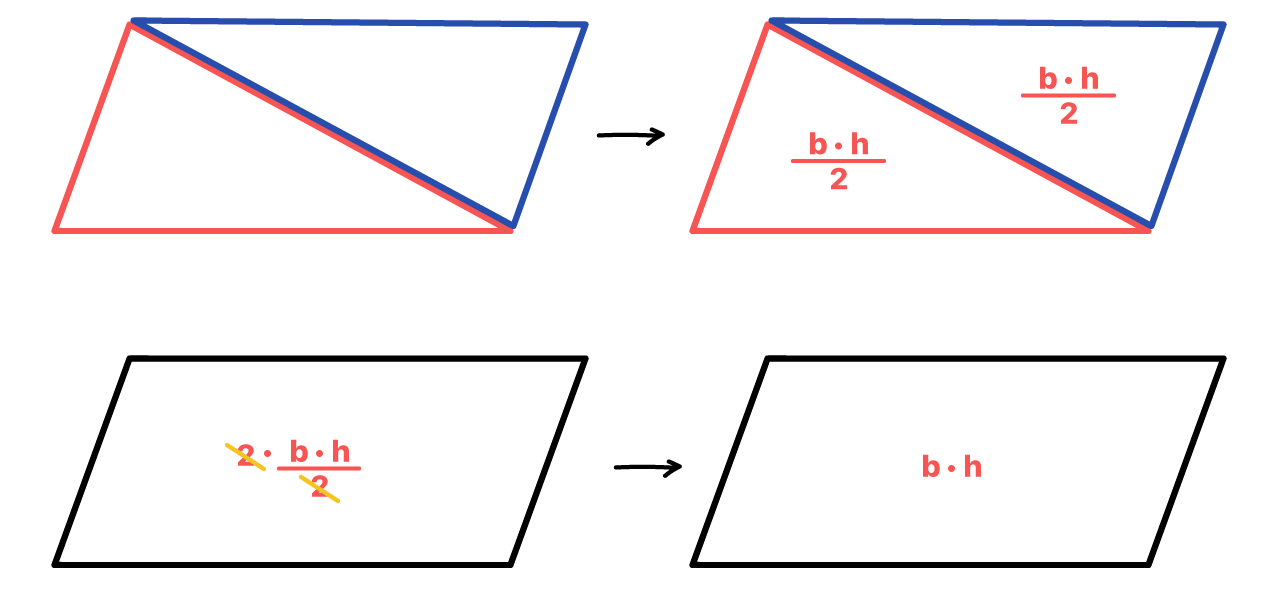
O fato é que todos os quadriláteros podem ser considerados como a união de dois ou mais triângulos. Vejam na imagem acima, que o paralelogramo é formado por dois triângulos. A fórmula da área do triângulo é equivalente a metade do produto entre a sua base e a sua altura. Aí eu pergunto: o que acontece quando unimos duas metades de um todo? Temos um valor inteiro, não é? Por isso, a área de um paralelogramo pode sim ser dada pelo produto entre a medida de sua base e a medida de sua altura.

Bom, chega de fórmulas por hoje! Vamos aplicar tudo que aprendemos nesse texto resolvendo um exercício bastante intrigante. Olhem só!

 

4. EXERCÍCIO RESOLVIDO

Na figura abaixo, ABCD é um paralelogramo de área igual a 24 cm². M e N são pontos médios de BC e CD, respectivamente. Determine a área do polígono AMND.

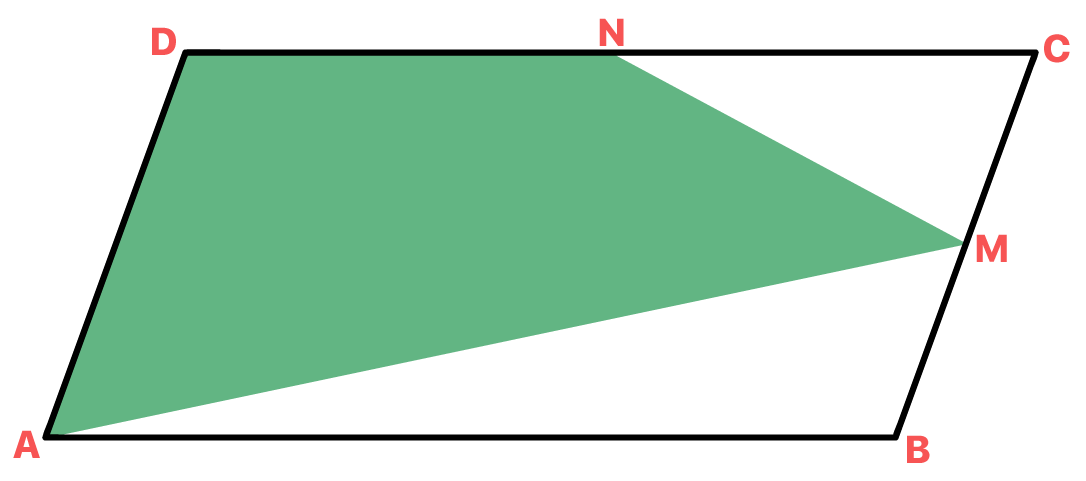
Vejam, pessoal, que o exercício está nos pedindo para calcular a área da polígono verde, que está dentro do paralelogramo. Mas assim, só de olhar, vocês saberiam dizer o nome dessa figura geométrica? Retângulo, paralelogramo, triângulo, losango, … Pois é, parece que não sabemos nada sobre ela. Agora, reparem nas partes que não pertencem a área verde dentro do paralelogramo. Não são triângulos? Opa, dessas figuras nós sabemos como encontrar a área!

É essa sacada que precisamos ter para resolver exercícios do ENEM e dos vestibulares. Às vezes a solução dos problemas não é óbvia, mas é muito simples! Nosso foco agora, será encontrar a área desses dois triângulos externos ao polígono AMND. Depois, é só descontar os resultados do valor da área do paralelogramo como um todo, os 24 cm² dados no enunciado.

Fazer uso do desenho é algo muito importante, principalmente na geometria plana. Nesse sentido, a fim de não nos perdermos na resolução do caso, chamaremos um dos triângulos da figura de número 1 e o outro de número 2.

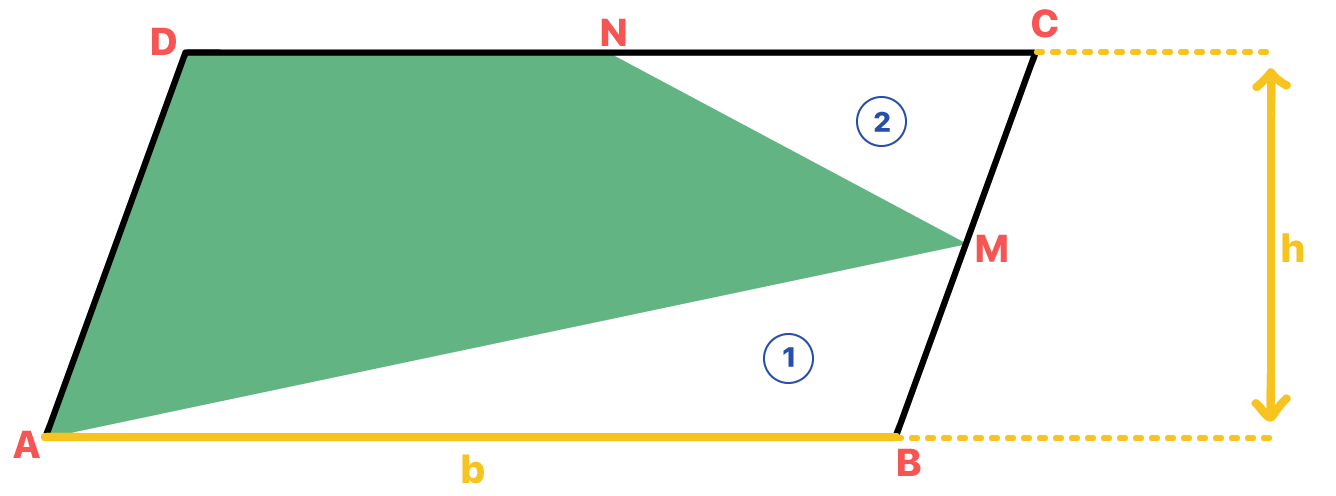
Observem que na imagem acima, também já estão identificadas as medidas da base e da altura do paralelogramo, como b e h, respectivamente. Assim, podemos afirmar com toda a certeza que:

24 = b × h

Certo, mas e a área dos nossos triângulos? Agora chegou o momento em que devemos interpretar direitinho como aqueles pontos M e N podem nos ajudar a resolver a questão.

 

Utilizando o conceito de ponto médio …

O próprio enunciado nos diz: “M e N são pontos médios de BC e CD, respectivamente”. Ora, se eles são pontos médios do segmento em que se encontram, então quer dizer que eles dividem esses segmentos pela metade, como vimos neste texto!

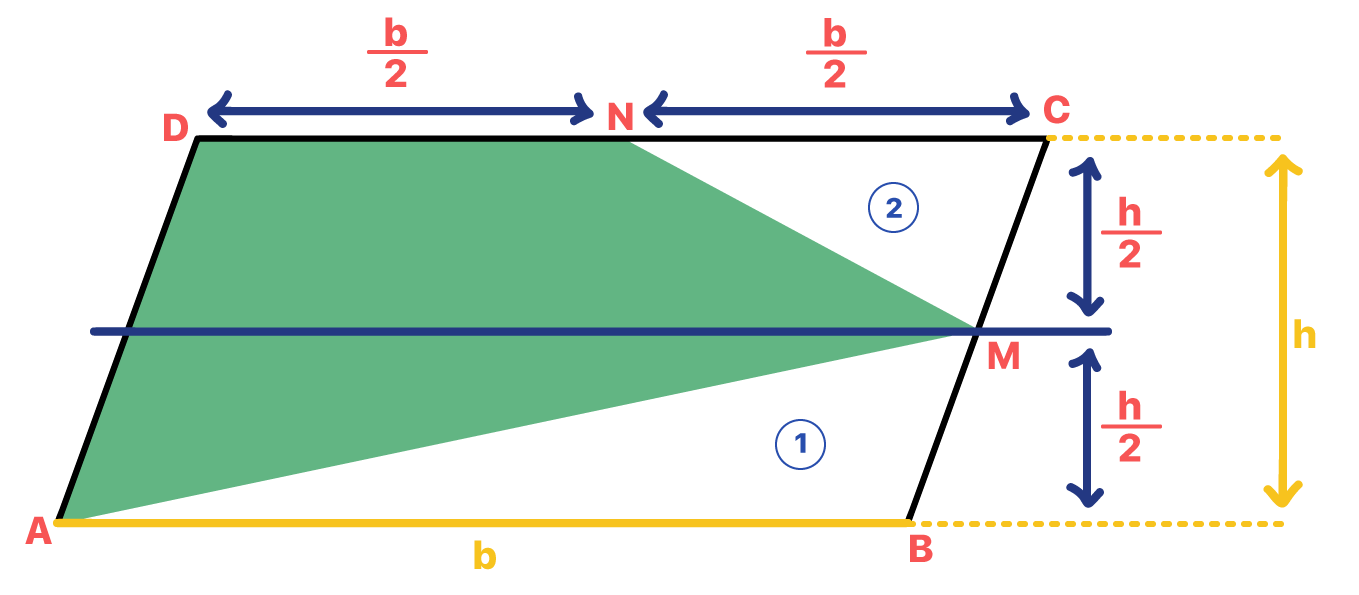
Conhecendo esse detalhe, nós conseguimos definir que a medida da base do triângulo 1 é igual a medida da base do paralelogramo, b. Já a sua altura, certamente será a metade da altura do paralelogramo, ou h/2, como mostra a imagem acima. Com relação ao triângulo 2, podemos perceber que a medida da sua base será a metade da medida da base do paralelogramo, ou seja, b/2, enquanto que sua altura, será igual a do triângulo 1, h/2. Substituindo esses valores na fórmula da área do triângulo, podemos chegar a algumas conclusões:

 

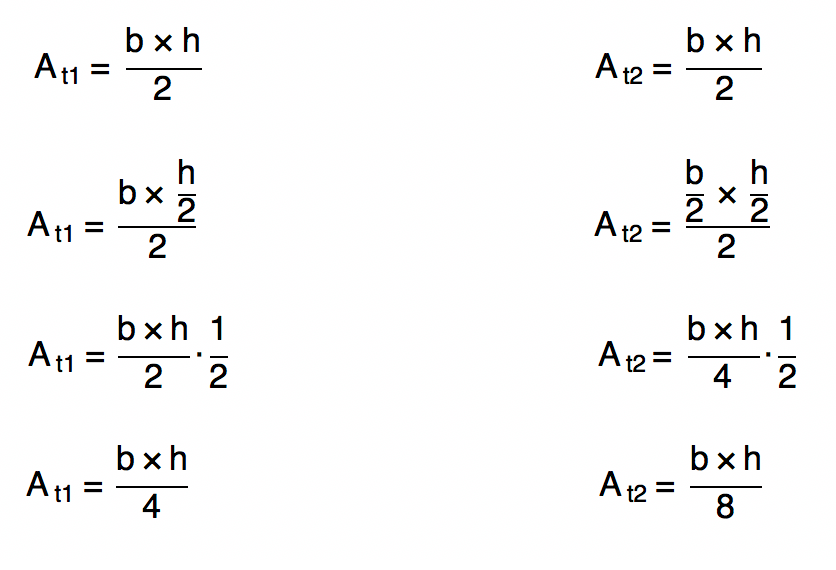
E agora …

Encontramos os valores das áreas de ambos os triângulos, contudo, o que fazer com as incógnitas b e h, que representam as medidas da base e da altura do paralelogramo? Pessoal, nós montamos uma equação para a área do paralelogramo no início desta resolução. Assim, sabemos que a multiplicação de b por h resulta em 24. Por isso, podemos substituir esse valor nas equações que acabamos de obter:

Neste momento, já temos condições de calcular a área da figura AMND que a questão nos pede. Vamos descontar da área do paralelogramo, as áreas dos dois triângulos que não compõem a figura.

A_AMND = A_{paralelogramo} – A_t1 – A_t2

A_AMND = 24 – 6 – 3

A_AMND = 15 cm²

Gostaram do exercício? É com ele que concluímos mais um texto! Espero que vocês tenham apreciado os conceitos do paralelogramo, e que possam aplicar com facilidade tudo o que aprendemos quando precisarem. E quem gostou do conteúdo, também pode ficar a vontade para conhecer a Plataforma do Professor Ferretto! Clique aqui para saber como ela funciona!

Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da Plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!

Em anexo, é claro, fica o vídeo que complementa o assunto. Deem uma olhada nele, garanto que vocês encontrarão mais alguns exercícios resolvidos e assim, estarão prontos para responder qualquer questão sobre o assunto!

Um abraço a todos! E ótimos estudos!