RELAÇÕES MÉTRICAS NA CIRCUNFERÊNCIA

Olá Pessoal! Tudo bem?

Vamos estudar mais um assunto sobre geometria plana, e neste texto vamos abordar algumas relações métricas na circunferência, bem como suas propriedades. Essas relações métricas são muito importantes no estudo da geometria plana, principalmente para você que irá fazer o Enem ou o vestibular. Então, eu espero que esse texto seja bastante útil para você nos seus estudos. Certo pessoal?!

Então, vem comigo aqui!

No estudo da circunferência, vamos ver algumas relações métricas na circunferência. Essas relações métricas eu irei abordar utilizando algumas propriedades. Vamos ver cada uma delas!

Antes de começar, uma dica muito importante. Se você quiser se aprofundar mais no estudo da geometria plana, assine a plataforma Professor Ferretto. Na plataforma você terá acesso a videoaulas, listas de exercícios, material didático e questões do Enem e do vestibular resolvidas.  

 

1. PROPRIEDADE DA TANGENTE:

Toda tangente a uma circunferência é perpendicular ao raio no ponto de tangência.

Vou exemplificar melhor esta propriedade para vocês usando a figura da circunferência apresentada abaixo.

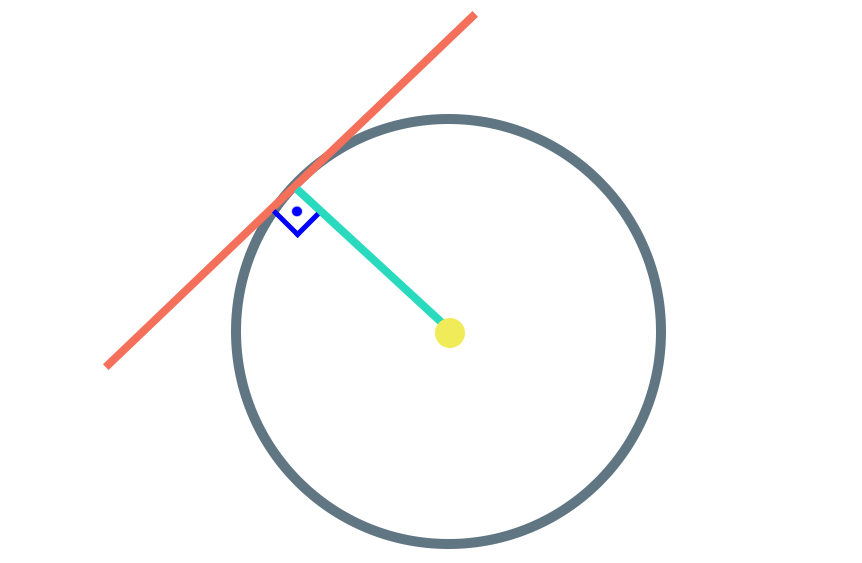
Vejam que temos uma reta tangente traçada junto a circunferência, isto ocorre porque essa reta está tocando a circunferência em apena um único ponto P, e os demais pontos da reta são externos à circunferência. Esse ponto em comum é chamado de ponto de tangência.

Ao traçarmos uma reta que liga o raio R ao ponto de tangência, podemos ver que a reta tangente e o raio são perpendiculares entre si, ou seja, formam um ângulo de 90°.

Vou fazer um exercício que aborda essa propriedade que acabamos de ver, para vocês aprenderem melhor.

 

1) As circunferências da figura abaixo são tangentes entre si e tangentes à reta r nos pontos A e B. Se os raios medem 8 cm e 2 cm, determine a medida do segmento AB.

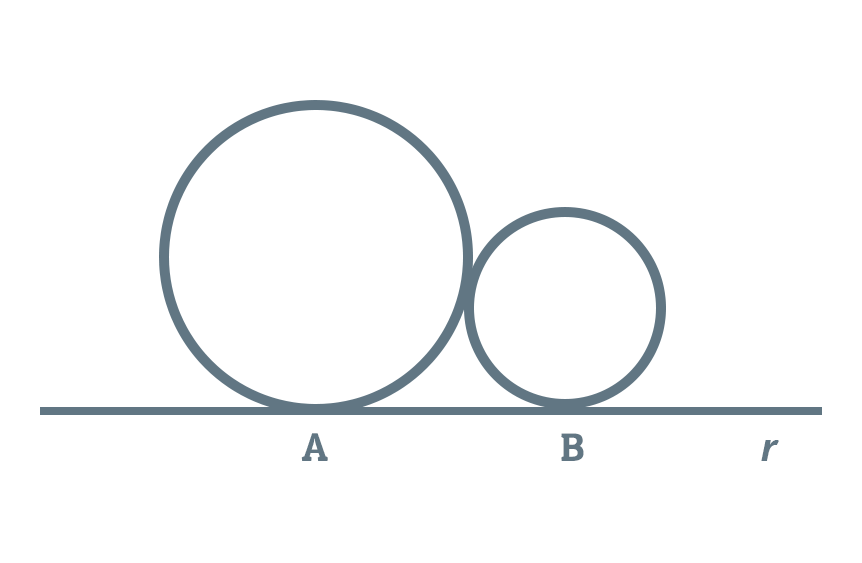
A questão pede o comprimento do segmento AB, então vou chamar esse segmento de x. Se nós unirmos os dois centros destas circunferências, teremos 8 cm do raio da circunferência maior e 2 cm do raio da circunferência menor, resultando em uma reta de 10 cm.

Como acabamos de ver na propriedade, ao traçarmos uma reta do centro da circunferência menor ao ponto de tangência B, o raio forma um ângulo de 90° com a reta tangente. Da mesma forma, ao ligarmos o raio da circunferência maior ao seu ponto de tangência A, temos um ângulo de 90° sendo formado. Notem que o comprimento da reta ao ponto de tangência B é de 2cm.

Agora imaginem o seguinte, que por esse ponto central da circunferência menor passamos uma reta paralela a reta r. Ao traçar esta reta, podemos perceber que a reta que liga o raio da circunferência maior ao ponto de tangência A, ficou dividida em duas partes. Uma de 2 cm abaixo da reta tangente a r e a outra de 6 cm acima desta reta, como exemplificado na figura abaixo.

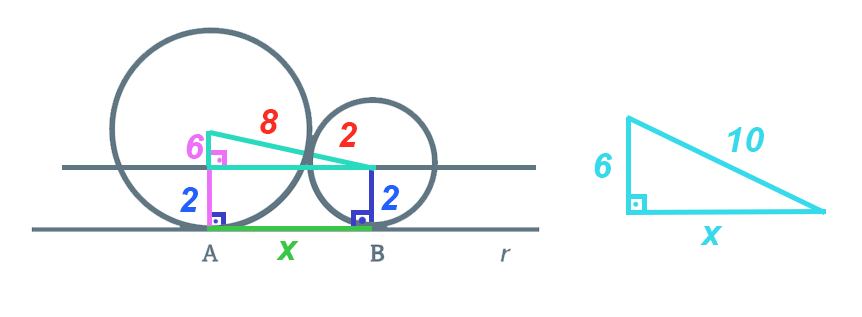
Vejam que nós temos um triângulo sendo formado, e este, com certeza, é um triangulo retângulo. O cateto que nós temos embaixo, é exatamente o mesmo comprimento do x que nós queremos descobrir nesta questão.

Podemos calcular a medida de x usando o Teorema de Pitágoras, já que temos o valor da hipotenusa e de um dos catetos.

Desta forma, podemos fazer:

a² = b² + c²

10²  = 6² + x²

x² = 100 – 36

x² = 64

x = ± 8

Neste caso, ficamos apenas com o valor positivo, já que refere-se a comprimento. Então, o segmento AB mede 8 cm.

 

2. PROPRIEDADE DA SECANTE

Um segmento de reta, que une o centro e o ponto médio de uma corda, é perpendicular a esta corda. Deixa eu explicar melhor, vejam a figura abaixo:

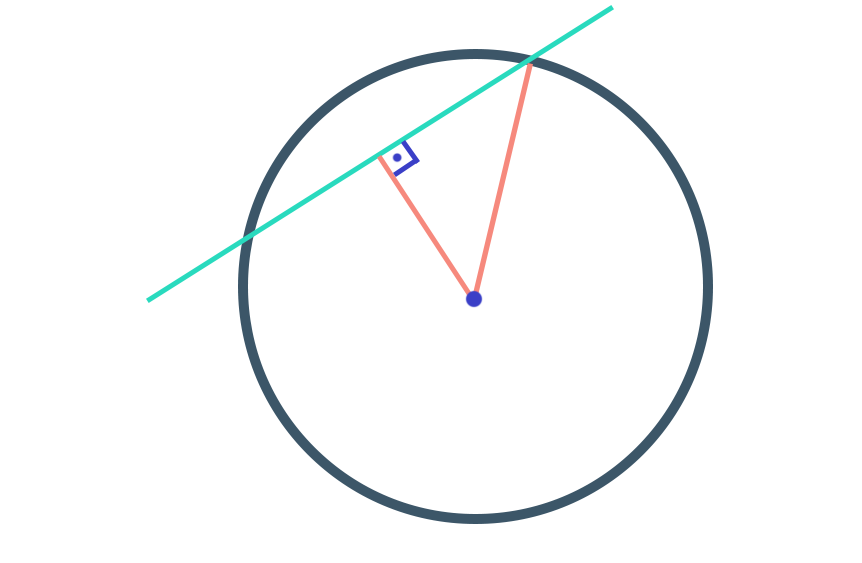
Notem que uma reta secante a circunferência é uma reta que intercepta a circunferência em dois pontos distintos, e essa secante tem na parte interna da circunferência a corda.

Neste caso, ao traçarmos uma reta ligando o raio R ao ponto médio da corda, também podemos perceber que ambas formam um ângulo reto entre si. Se nós pegarmos o raio e colocarmos ele perpendicularmente a corda, você pode ter certeza que esta corda ficará dividida em dois segmentos que possuem o mesmo comprimento.

Agora vamos fazer um exemplo em relação a esta propriedade. Neste caso, é importante que vocês saibam que distância de reta ou segmento de reta a um ponto, sempre consideramos ela formando um ângulo de 90°, ou seja, sempre a menor distância em relação ao ponto.

2) Em uma circunferência de 13 cm de raio, uma corda, de 24 cm de comprimento está a que distância do centro dessa circunferência.

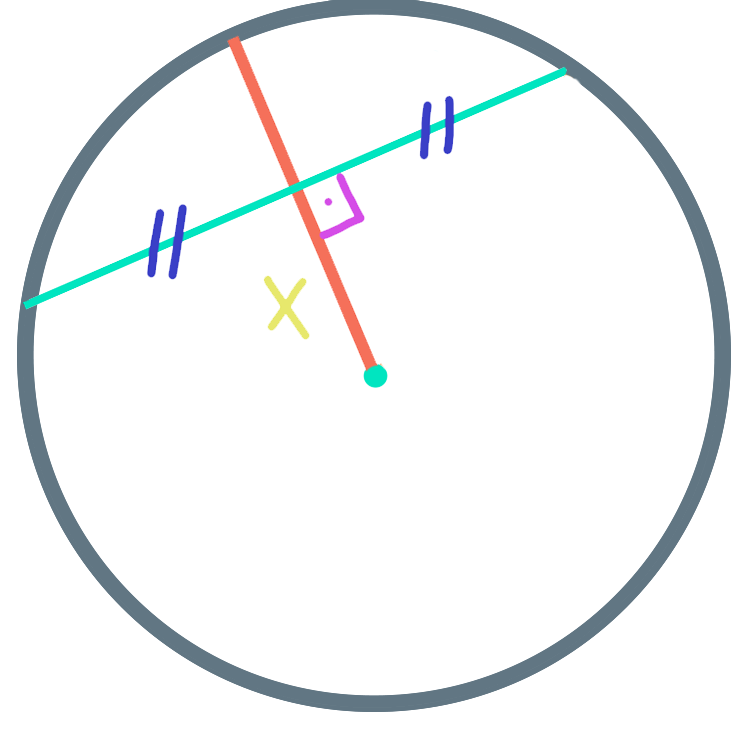
Vamos ligar o raio perpendicularmente a corda, a qual ficará dividida em dois segmentos de 12 cm em cada lado, pois seu comprimento total é de 24 cm.

Notem que o raio da circunferência mede 13 cm, então, nós podemos traçar este raio junto a borda da circunferência como mostra a figura abaixo.

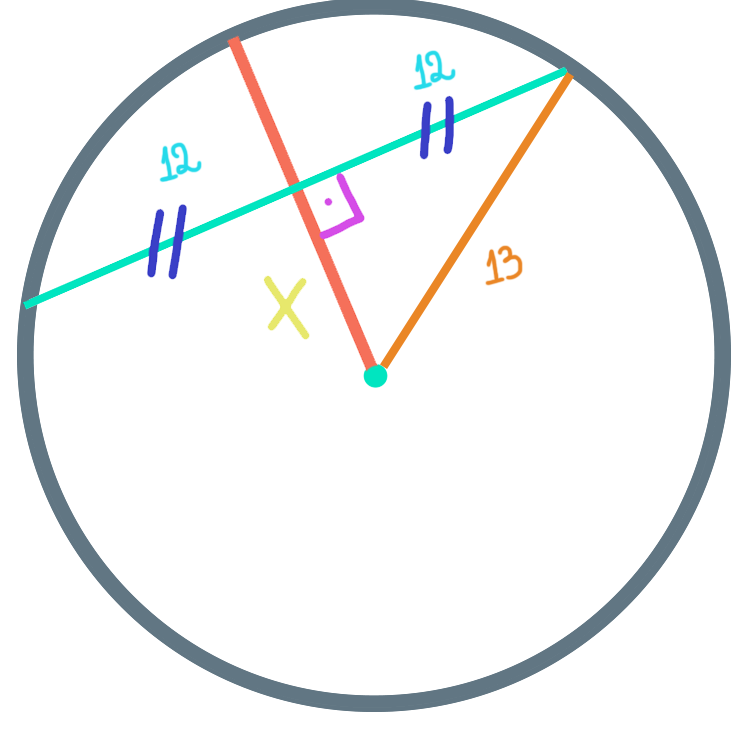
Pessoal, vejam que foi formado um triângulo retângulo, e nós podemos montar o teorema de Pitágoras.

13² = 12² + x²

169 – 144 = x²

x

x= ± 5

Então, a distância do raio a corda mede 5 cm, ou seja, a distância da corda até o centro mede 5 cm.

 

3. SEGMENTOS TANGENTES

Se de um ponto P conduzirmos os segmentos PA e PB, ambos tangentes a uma circunferência, com A e B na circunferência, então PA ≡ PB.

Vejam a circunferência abaixo, na qual existem dois segmentos tangentes à ela e ligados por um ponto P. Com os pontos A e B na circunferência, temos um segmento PA e outro segmento PB, dois segmentos congruentes, ou seja, de mesmo comprimento. Desta forma podemos dizer que o comprimento de PA é o mesmo de PB.

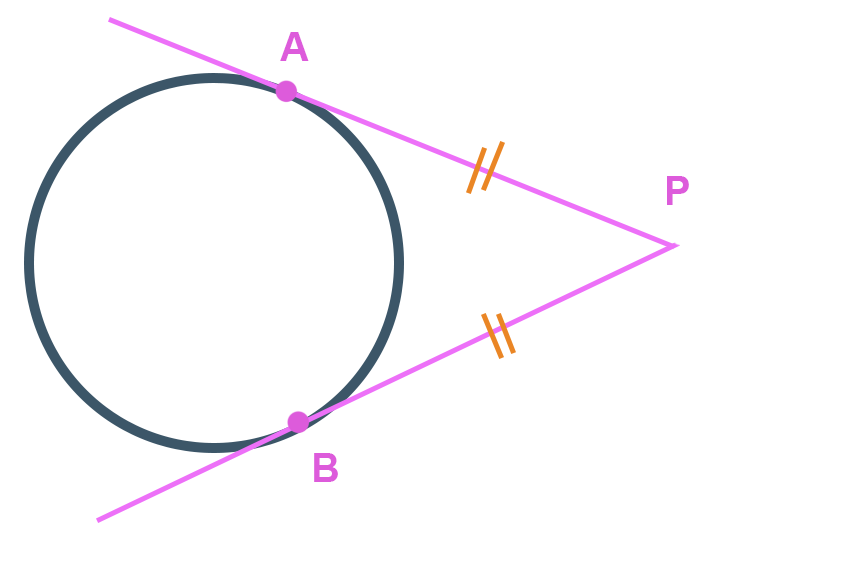
Pessoal, vamos fazer um exemplo que aborda esta propriedade para vocês entenderem melhor.

Na figura abaixo, PA = 12 cm. Determine o perímetro do triângulo PDE.

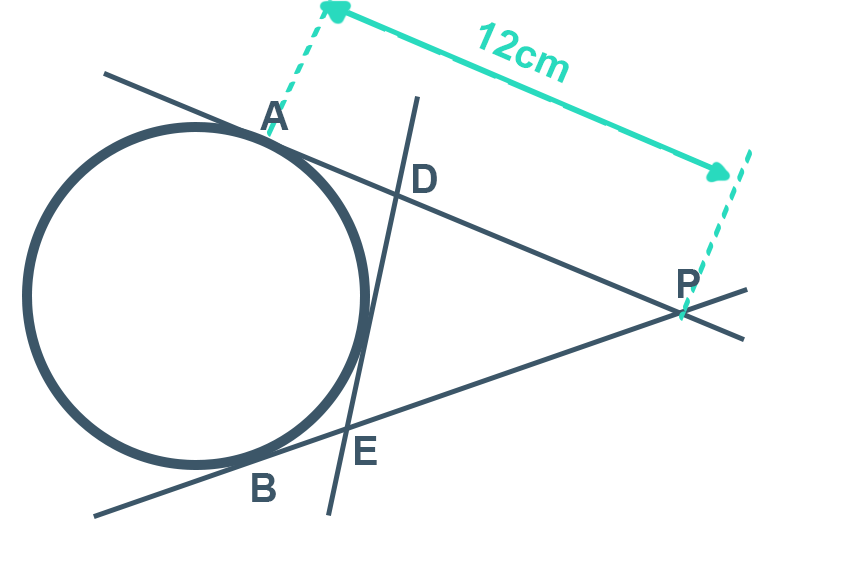
Vejam que do ponto P externo estamos traçando duas retas tangentes, então, de acordo com a propriedade, a distância de PB também vale 12 cm.

Agora, reparem o seguinte: do ponto D nós estamos traçando uma tangente pelo lado direito e uma tangente por cima da circunferência. Dessa forma, podemos ver que o comprimento de D até A é igual ao comprimento de D até o ponto de tangência. Então se nós dissermos que o segmento DA valerá a, o outro segmento também vale a, de acordo com a propriedade que nós acabamos de ver.

Usando o mesmo raciocínio, o ponto B é um ponto tangente e o E é um ponto externo a circunferência. Assim, se nós dissermos que o comprimento do segmento que vai de E até B vale b, o segmento que vai de E até o ponto de tangência também valerá b.

Como a questão pede para calcular o perímetro do triângulo PDE, devemos calcular a soma de todos os lados do triângulo PDE. Para isso devemos analisar dois lados:

– o lado PD que é igual ao todo menos o comprimento a, então, PD = 12 – a;

– o lado PE que é igual ao todo menos o comprimento b, logo, PE = 12 – b.

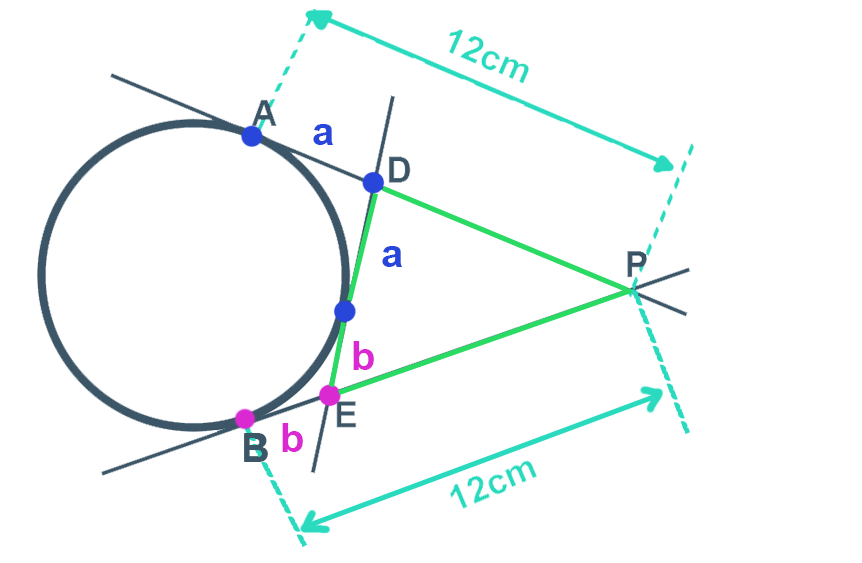
Com isso podemos calcular o perímetro do triângulo PDE. Na geometria o perímetro é representado por 2p, ou seja, 2 semiperímetro:

2p = P = (12 – a) + a + (12 – b) + b

P = 12 – a + a + 12 – b + b

P = 24

Então, o perímetro do triângulo PDE é de 24 cm.

 

4. QUADRILÁTERO CIRCUNSCRITO

Se um quadrilátero convexo é circunscrito a uma circunferência, a soma de dois lados opostos é igual à soma dos outros dois.

Um quadrilátero convexo é circunscrito a uma circunferência se, e somente se, seus quatro lados são tangentes a circunferência. Deixem eu explicar melhor.

Como no exemplo abaixo, temos um quadrilátero que está circunscrito na circunferência, ou seja, que está por fora da circunferência, mas não simplesmente por fora, notem que todos os lados do quadrilátero estão tangenciando a circunferência. Se definirmos os lados como a, b, c e d, pela propriedade sabemos que:

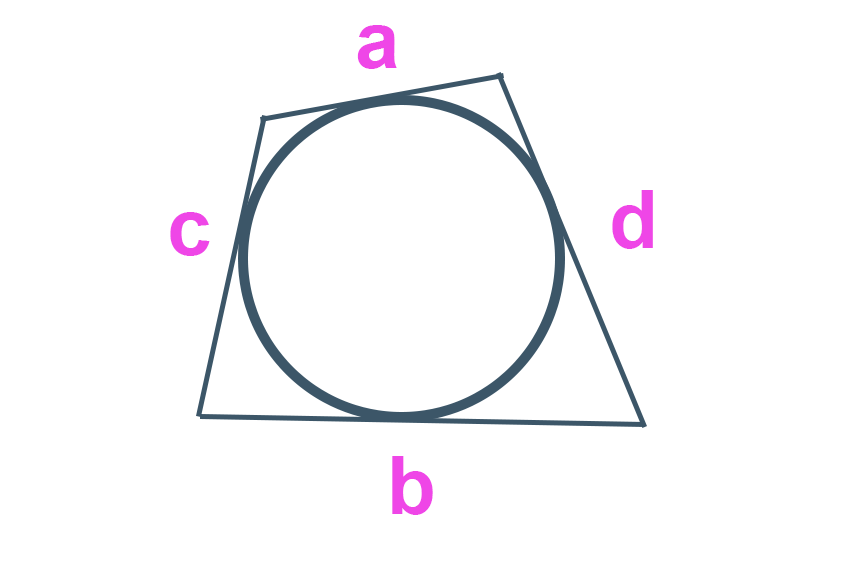
A + B = C + D

Pessoal, essa propriedade também é uma condição necessária para que nós possamos colocar uma circunferência inscrita nesse quadrilátero. Por exemplo, vejam o retângulo abaixo, veja que nós não podemos colocar uma circunferência inscrita nele de tal forma que os quatro lados do retângulo estejam tangenciando a circunferência. Isto ocorre porque a soma dos lados opostos do retângulo não é igual.

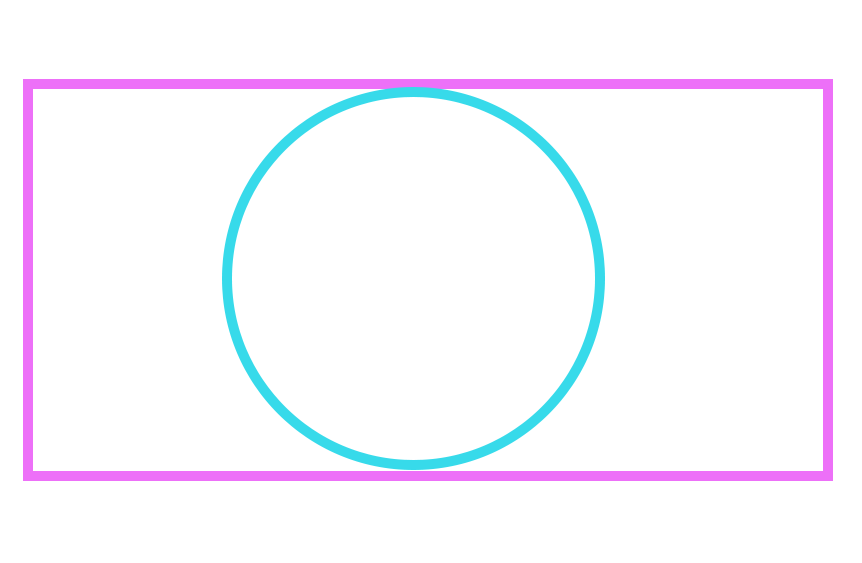
Então, a soma dos lados opostos serem iguais em um quadrilátero é uma condição para que nós possamos colocar uma circunferência inscrita no mesmo.

Vamos fazer um exemplo que aborde esta propriedade e para que fique bem claro pra vocês como usar ela.

Determine o perímetro do quadrilátero abaixo.

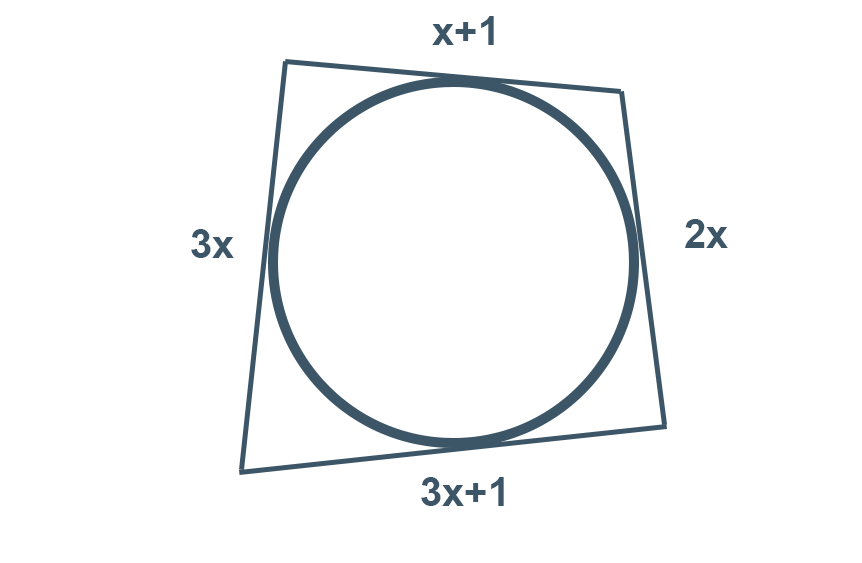
Reparem que os quatro lados do quadrilátero estão tangenciando a circunferência, ou seja, nós temos um quadrilátero circunscrito na circunferência. Como vimos na propriedade, a soma dos lados opostos devem ser iguais, então:

3x + 2x = x + 1 + 3x + 1

5x = 4x + 2

5x – 4x = 2

x = 2

Desta forma, se o x vale dois, podemos descobrir o valor de cada lado deste quadrilátero.

   i. 3x = 3.2 = 6

  ii. 3x + 1 = 3.2 +1 = 7

 iii. 2x = 2.2 = 4

iv. x + 1 = 2 + 1 = 3

Somando todos os lados teremos um perímetro de:

P = 6 + 7 + 4 + 3

P = 20 cm

Finalizamos mais um texto e eu espero que tenha sido muito proveitoso e importante para o seu estudo de geometria. Deixo em anexo o vídeo do conteúdo para que vocês possam assistir e acompanhar o que foi aprendido no texto de hoje.

Bons estudos, sucesso e até mais!