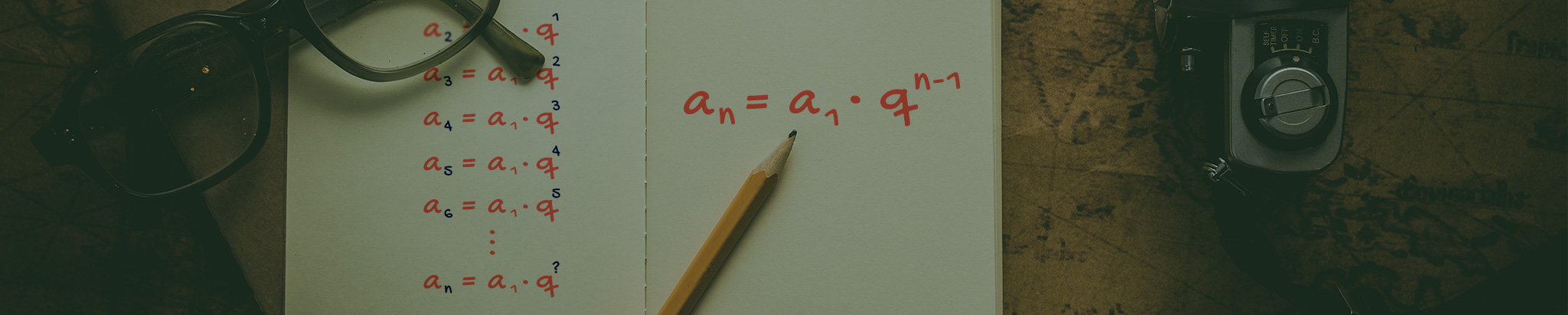Uma progressão geométrica (PG) é uma sequência em que cada termo, a partir do segundo, é o produto do anterior por uma constante q dada. Dependo do valor de q, e do primeiro termo da sequência, a₁, é possível classificar uma PG como crescente, decrescente, constante ou alternada.

 

Olá, pessoal! Tudo bem por aí?

No texto de hoje, falaremos sobre uma sequência numérica muito conhecida, a progressão geométrica, ou simplesmente PG. Diferente da PA, a PG se caracteriza por crescer ou decrescer através do produto de seus termos por um valor constante. Isso faz com que os termos da sequência cresçam ou decresçam muito mais rápido que na progressão aritmética, um fenômeno que possui inúmeras aplicações. E se tem aplicação no cotidiano, podem ter certeza que a PG vai aparecer nas provas dos vestibulares e também no ENEM!

Certo, pessoal? Então, vem comigo desvendar os segredos da PG!

 

1. PA vs. PG

Observem a sequência numérica abaixo:

(3, 6, 12, 24, 48, ….)

O primeiro detalhe ao qual daremos ênfase, é que cada termo da sequência apresentada possui uma posição definida. O número 3 é o primeiro termo da sequência, 6 é o segundo, 12 é o terceiro e assim por diante. Por isso, nós chamaremos esses termos de a₁, a₂, a₃, a₄, a₅, como mostra a imagem abaixo.

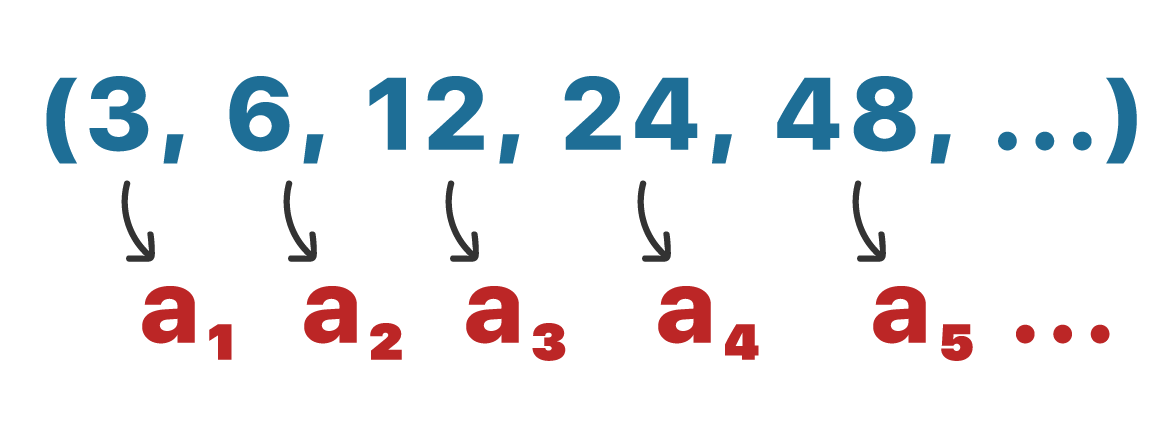
Agora, vamos lembrar de outra famosa progressão, a PA, que estudamos no texto Definição e Classificação de uma Progressão Aritmética. Nós vimos lá, que para uma sequência formar uma progressão aritmética, a diferença entre quaisquer dois de seus termos consecutivos deve ser sempre um número constante. Bom, vamos aplicar essa ideia na sequência acima, e ver o que acontece!

a₂ – a₁ = 6 – 3 = 3

a₃ – a₂ = 12 – 6 = 6

a₄ – a₃ = 24 – 12 = 12

a₅ – a₄ = 48 – 24 = 24

Pois é, parece que aqui a diferença entre quaisquer termos consecutivos da sequência não resulta em um termo constante, afinal, todos os resultados obtidos foram sempre diferentes. Isso significa que a sequência (3, 6, 12, 24, 48, ….) não é uma PA. Mas e se vocês tentassem dividir qualquer um dos termos que não o primeiro pelo seu antecessor, o que aconteceria?

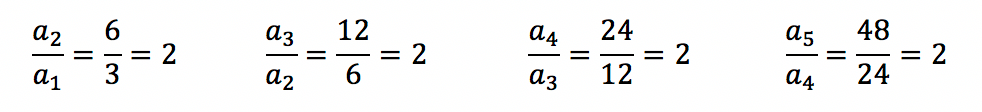
Vejam que desta forma o resultado foi sempre um termo constante, de valor 2. Isso é um sinal de que ainda temos muito a estudar sobre essa sequência. Vamos descobrir agora, como definir a progressão geométrica. Vem comigo!

 

2. O QUE É UMA PROGRESSÃO GEOMÉTRICA?

Uma PG é uma sequência em que cada termo, a partir do segundo, é o produto do anterior por uma constante q, a razão da progressão. Vamos desenrolar esse conceito reescrevendo a sequência que estávamos analisando:

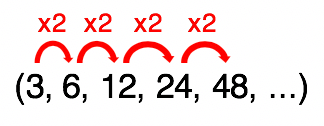
6 é o produto de 3 por 2. 12 é produto de 6 por 2. 24 é o produto de 12 por 2 e daí por diante. Portanto, a sequência (3, 6, 12, 24, 48, ….) é uma progressão geométrica de razão q igual a 2.

 

3. QUAL É A FÓRMULA DA RAZÃO DE UMA PG?

Quando comparamos a progressão geométrica com a progressão aritmética, nós resolvemos dividir dois termos consecutivos da sequência exemplo. Para nossa surpresa, o resultado foi sempre a mesma constante. Isso nos permite enxergar a PG sob um segundo ponto de vista. Quando a divisão ou o quociente entre dois termos consecutivos de uma sequência resultar em um valor constante, significa que se trata de uma progressão geométrica!

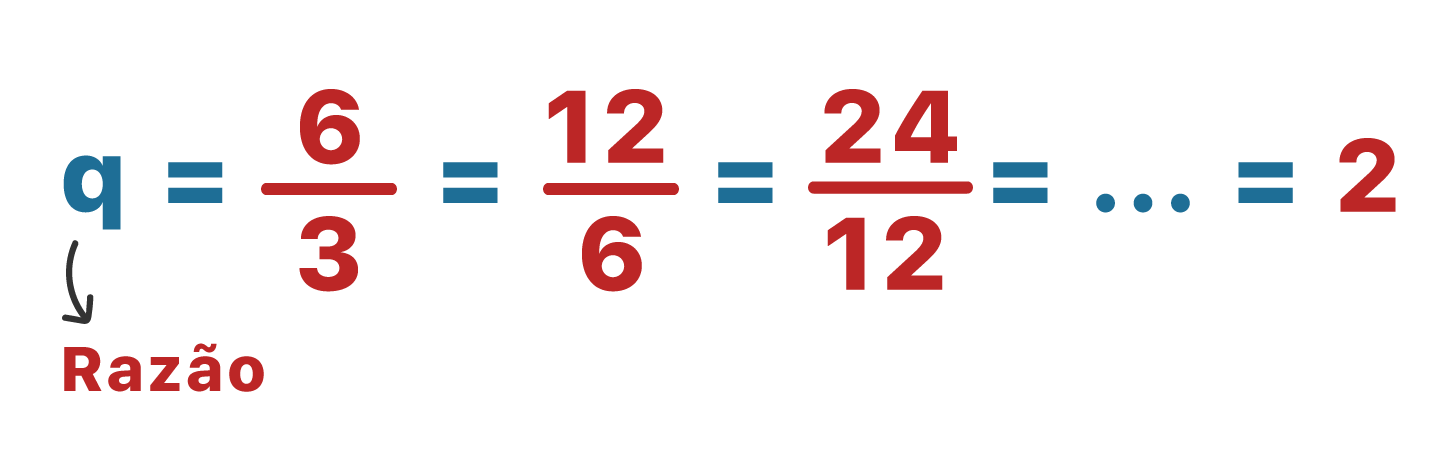
Assim, podemos partir de uma fórmula geral, e determinar uma série de fórmulas que nos permitem encontrar a razão da PG. Tudo depende dos termos da sequência cujos valores são conhecidos!

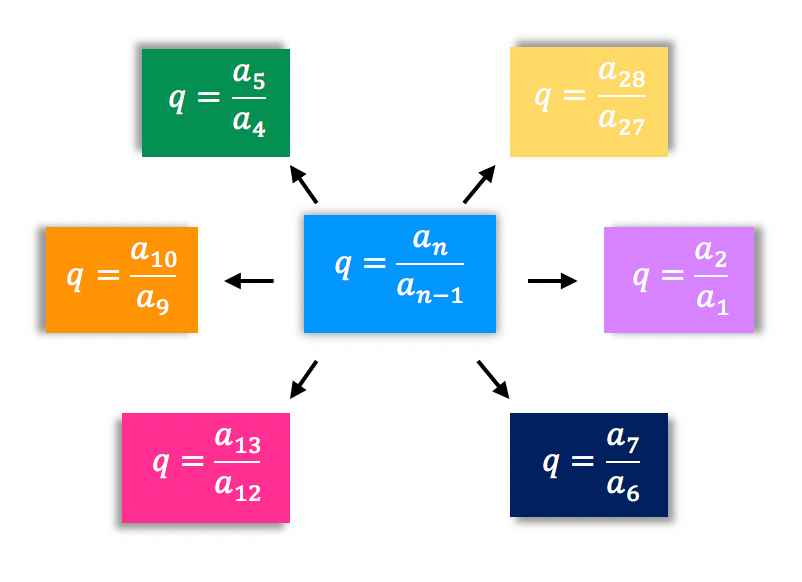
Entendido? Então vamos praticar a ideia através de um exemplo resolvido. Sigam comigo!

 

4. EXEMPLO RESOLVIDO SOBRE A PROGRESSÃO GEOMÉTRICA

Encontre os próximos termos de uma PG de razão 3, cujo primeiro termo vale 2.

Tranquilo, não é pessoal? Segundo a definição, uma progressão geométrica é formada quando cada um de seus termos é o produto do termo antecessor pela razão q. Desta forma, basta multiplicarmos o primeiro termo da PG dada por 3, e seguir multiplicando cada um dos termos seguintes pela mesma razão q.

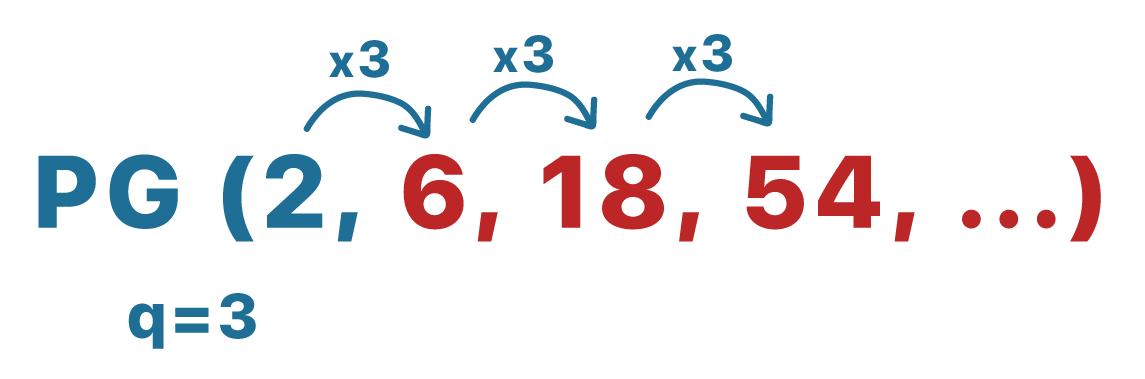
Bem, se vocês repararem melhor na sequência que acabamos de apresentar, verão que os termos são números cada vez maiores, tendendo ao infinito. Mas a verdade é que também existem sequências em que os termos são cada vez menores, ou seja, se aproximam cada vez mais de zero ou de menos infinito.

Também não dá para se assustar, se vocês encontrarem sequências em que os termos não se alteram, ou mudam de sinal constantemente. Todos esses casos podem formar uma progressão geométrica, como veremos a seguir.

 

5. CLASSIFICAÇÃO DE UMA PROGRESSÃO GEOMÉTRICA

As progressões geométricas podem ser classificadas em quatro categorias: crescente, decrescente, constante e alternada. Tudo depende do valor do termo a₁, ou seja, do primeiro termo de cada sequência, e também de sua razão q. A seguir, veremos cada uma das classificações detalhadamente e com a ajuda de alguns exemplos.

 

5.1 PG crescente

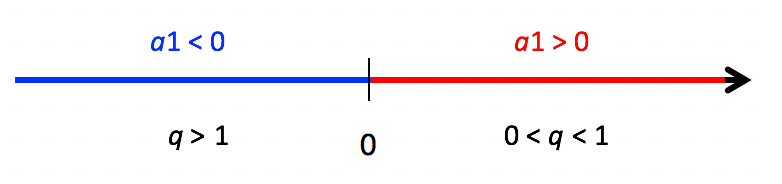
Existem duas formas de construir uma progressão geométrica crescente. Caso o primeiro termo da sequência, a₁, seja positivo, então a razão q da progressão deve necessariamente ser maior do que 1. Já se a₁ for negativo, tem-se que a razão q deve ser um valor entre 0 e 1.

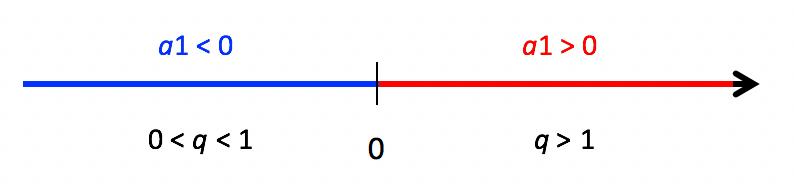
Querem ver como faz sentido? Vamos analisar duas sequências classificadas como PG crescentes:

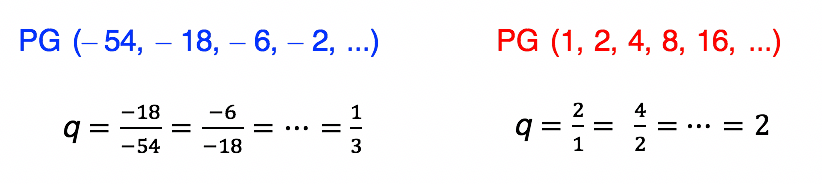
Reparem na PG destacada em azul. Seu primeiro termo é negativo, ou seja, a₁ < 0. Mas como a razão q da progressão é um valor entre 0 e 1, mais precisamente a dízima periódica 0,3333…, os termos da sequência vão crescendo, e ficando cada vez menos negativos.

Já na PG destacada em vermelho, ocorre uma situação diferente. Seu primeiro termo é positivo, ou seja, a₁ > 0. Assim, sendo a razão q maior do que 1, os termos da sequência tendem a crescer cada vez mais, e seguir rumo ao mais infinito.

Agora, digamos que por engano nós trocássemos as razões das duas progressões do exemplo. A primeira, cujo a₁ é negativo, teria uma razão de valor 2. Enquanto isso, a segunda, cujo primeiro termo é positivo, teria uma razão de valor 1/3. Recalcularam os demais termos aí? Se vocês não encontraram uma PG crescente, é porque estão no caminho certo! Neste caso, formaremos uma PG tal qual a do item seguinte.

 

5.2 PG decrescente

Também existem duas formas de construir uma progressão geométrica decrescente. Neste caso, se o primeiro termo da sequência, a₁, for positivo, a razão q da progressão deve necessariamente ser um valor entre 0 e 1. Do contrário, ou seja, se a₁ for negativo, a razão q deve ser um valor maior do que 1.

Para entendermos essa ideia direitinho, vamos montar as sequências que propus no item anterior.

Viram como deu certo? Quando multiplicamos um número negativo por um número maior que 1, o resultado será ainda mais negativo. Por isso, na sequência destacada em azul, os termos estão decrescendo, são cada vez menores, e tendem ao menos infinito.

Já quando multiplicamos um número positivo por um valor que se situa entre 0 e 1, isto é, por um número fracionário ou decimal, a tendência é que o resultado seja um valor próximo de zero. Assim, também se observa um comportamento decrescente, os termos vão diminuindo ao longo da sequência.

 

IMPORTANTE

Bom, pessoal, antes de seguirmos nosso texto, farei uma breve ressalva. Nós falamos sobre as características das progressões geométricas crescentes e decrescentes prestando bastante atenção no primeiro termo da sequência, o a₁ e na razão q da progressão. Mas é claro que vocês não precisam decorar tudo isso!

Fiquem sempre atentos ao comportamento da sequência. Se os termos estão crescendo ou aumentando ao longo da mesma, trata-se de uma PG crescente. Agora, se os termos estiverem decrescendo ou diminuindo ao longo da sequência, será uma PG decrescente. Essa é uma regra geral que vale tanto para a PA quanto para PG.

 

5.3 PG constante

Uma progressão geométrica é constante quando sua razão q é igual a 1. Desta forma, todos os termos da sequência serão sempre iguais. Para entender a lógica deste tipo de PG, é só lembrar do elemento neutro da multiplicação: o produto de qualquer número por 1, é sempre igual a ele mesmo!

 

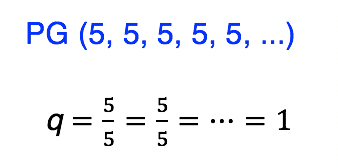
5.4 PG alternada

 

Uma progressão geométrica alternada ou oscilante, é aquela cuja razão q é negativa, ou seja, q < 0. Quando a razão de uma PG é negativa, acontece um fenômeno muito interessante: os termos da sequência acabam oscilando entre valores positivos e negativos. Podemos observar esse comportamento no exemplo abaixo:

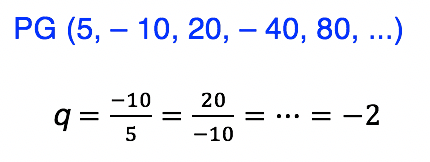
Entendido, pessoal? Depois de tudo o que acabamos de aprender, está mais do que na hora de encerrarmos este texto! Espero que os conceitos introdutórios da PG estejam mais claros agora, afinal, é muito importante que vocês saibam diferenciar quando uma sequência forma uma PA ou uma PG. Assim, tenho certeza de que utilizarão os conceitos certos para resolver questões que envolvem o assunto no ENEM e nos vestibulares!

Gostou deste conteúdo? Clique aqui para saber como a Plataforma do Professor Ferretto funciona!

Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da Plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!

Em anexo, estou deixando um vídeo no qual vocês podem revisar todo o conteúdo com mais alguns exemplos.

Um abração a todos! Nos vemos no próximo texto!