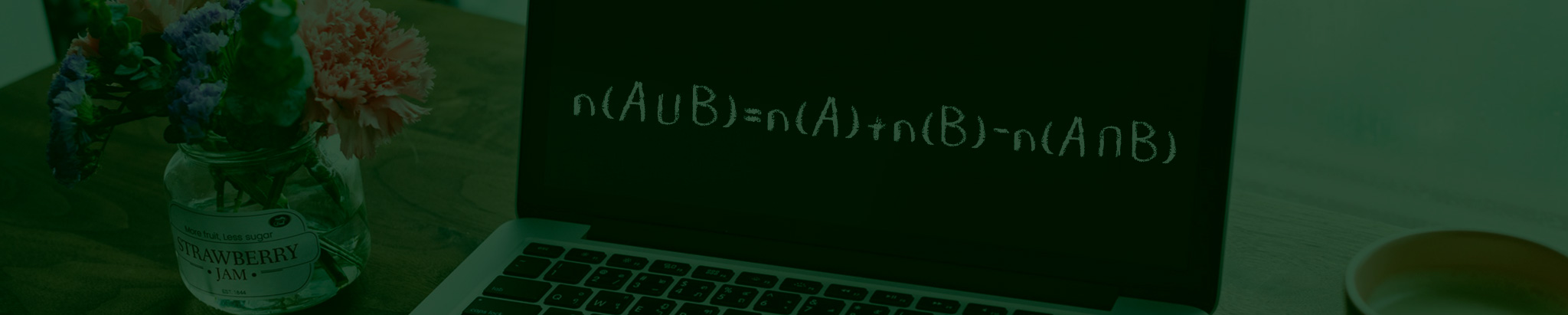A união de dois conjuntos A e B, é o conjunto formado pelos elementos que pertencem a A ou a B. Já a intersecção de A e B, pode ser dita como o conjunto formado pelos elementos que pertencem a A e a B.  Isso nos mostra que as conjunções “ou” e “e” tem um papel importante nas operações com conjuntos.

 

Olá, pessoal! Tudo bem por aí?

A partir de hoje, as conjunções ou e e vão ganhar um novo significado na vida de vocês! Elas conseguem exprimir exatamente o que significa a união e a intersecção entre dois conjuntos. Esse é um assunto da matemática do ensino médio extremamente importante para aqueles que desejam realizar as provas do ENEM e dos mais variados vestibulares. Por isso, se vocês são estudantes do ensino médio, ou irão prestar algumas dessas provas, eu peço: não deixem de acompanhar esse texto!

Certo, pessoal? Antes de tratarmos da união e da intersecção em si, que são duas operações fundamentais da teoria de conjuntos, é imprescindível revisarmos alguns conceitos importantes. Vem comigo!

 

1. REVISANDO A TEORIA DE CONJUNTOS

Dados dois conjuntos A e B, vejam o que pode acontecer quando estes possuem, ou não, elementos em comum:

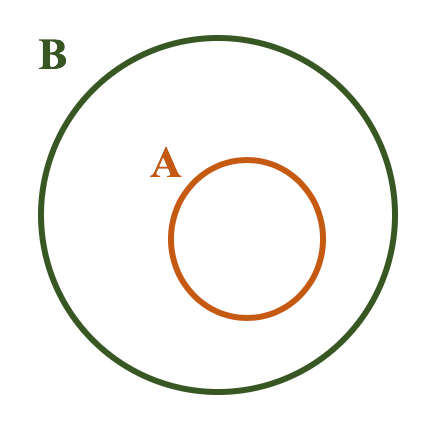
• Caso todos os elementos de A também pertençam ao conjunto B, fica evidente que A é subconjunto do conjunto B, ou que A está contido em B, ou ainda que A é parte de B. A representação em forma de diagrama de um caso como esse é apresentada na imagem abaixo:

• Caso nenhum elemento de A também pertença ao conjunto B, e claro, nenhum elemento de B também pertença ao conjunto A, pode se dizer que A e B são conjuntos disjuntos. Nesse caso, o diagrama de cada um dos conjuntos é representado da seguinte forma:

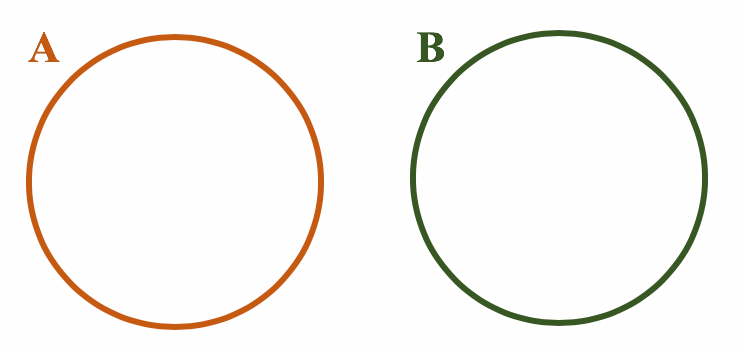
• E, por fim, pode ser que apenas alguns elementos do conjunto A também pertençam ao conjunto B e vice-versa. Nesse caso, é comum entrelaçar os diagramas, para que os elementos comuns a ambos os conjuntos se localizem na região comum aos dois diagramas, como mostra a imagem:

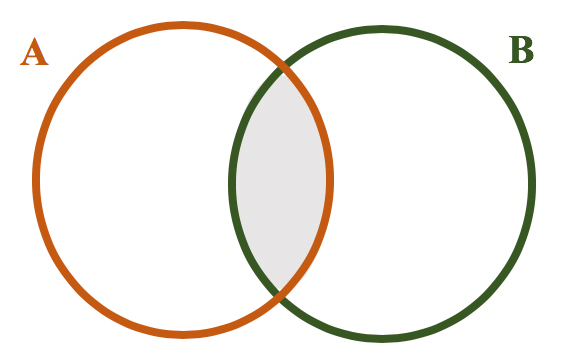
Neste momento, nós já estamos preparados para saber tudo sobre a união e a intersecção entre dois conjuntos. Então, vem comigo aqui!

 

2. UNIÃO

Dados dois conjuntos A e B, chama-se união de A e B o conjunto formado pelos elementos que pertencem ou a A ou a B.

O quadro abaixo mostra como é possível definir a união entre dois conjuntos A e B em forma de símbolos:

Observem que a união entre dois conjuntos é representada pelo símbolo “∪”. Assim, podemos afirmar que a união de A e B é o conjunto formado pelos elementos x, tais que esses elementos x pertençam ou ao conjunto A ou ao conjunto B ou a ambos os conjuntos.

O ou, dentro das classes gramaticais, é uma conjunção coordenativa alternativa. E uma alternativa pode ser dita como “uma de duas ou mais possibilidades pelas quais se pode optar”. Portanto, basta que um elemento pertença a um dos conjuntos citados, e ele fará parte da união entre esses dois conjuntos. Olhem só como destacamos a região que representa a união entre dois conjuntos A e B nos 3 casos que revisamos no início do texto:

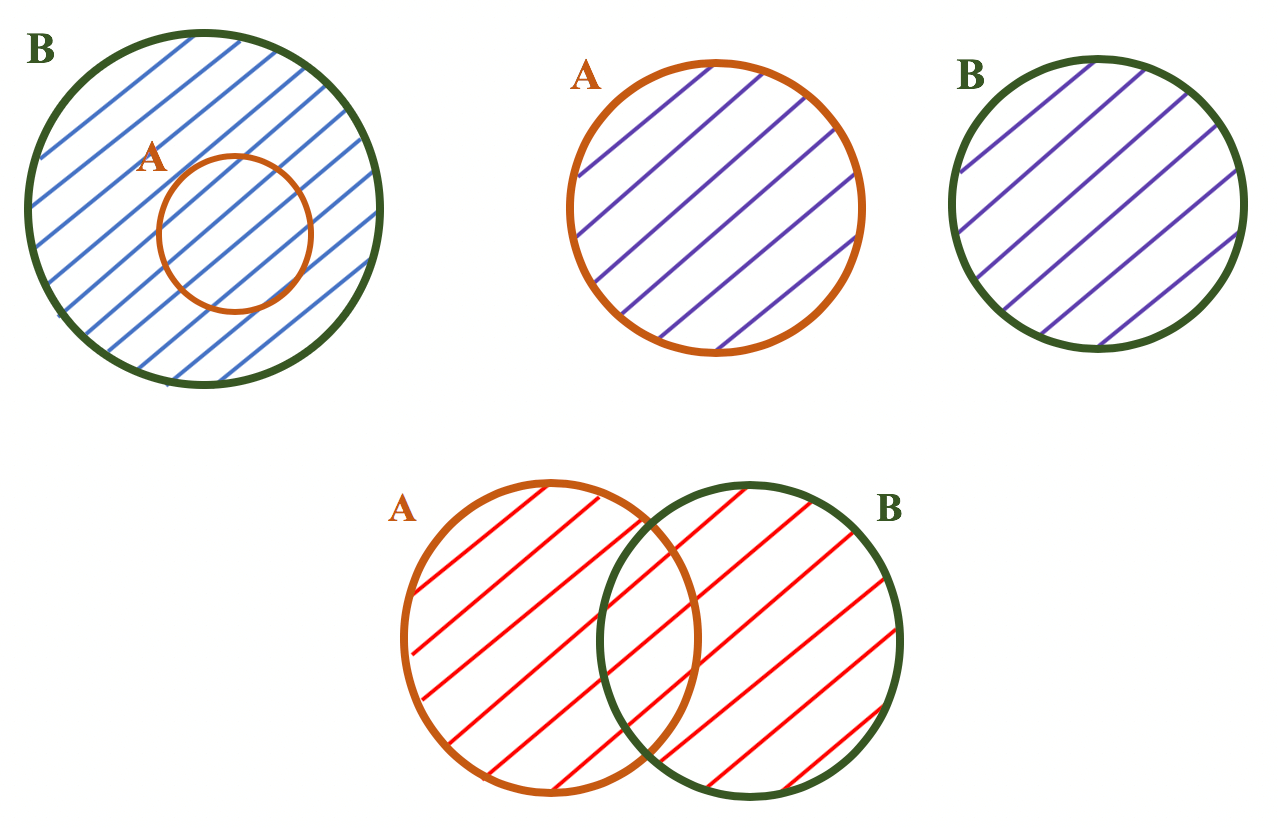
Vejam como a característica da união acaba por abranger todos os elementos dos conjuntos que são analisados. Isso acontece porque, para pertencer ao conjunto união, é possível, mas não é necessário, que os elementos pertençam a ambos os conjuntos, desde que pertençam a pelo menos um deles. Vocês verão agora, como a intersecção entre dois conjuntos se mostra bastante diferente do que acabamos de estudar.

 

3. INTERSECÇÃO

Dados dois conjuntos A e B, chama-se intersecção de A e B o conjunto formado pelos elementos que pertencem a A e a B.

O quadro abaixo mostra como é possível definir a intersecção entre dois conjuntos A e B em forma de símbolos:

A intersecção entre dois conjuntos é representada pelo símbolo “∩”. Assim, podemos afirmar que a intersecção de A e B é o conjunto formado pelos elementos x, tais que esses elementos x pertençam tanto ao conjunto A quanto ao conjunto B, ou seja, que esses elementos pertençam a ambos os conjuntos.

O e, dentro das classes gramaticais, é uma conjunção coordenativa aditiva. A palavra “aditiva” vem de adicionar, e quando realizamos uma adição, realizamos essa operação entre dois termos, ou dois valores. Essa ideia pode nos ajudar a entender a intersecção. Para que um elemento faça parte da intersecção entre dois conjuntos, não é suficiente que ele pertença somente a um dos conjuntos analisados, ele deve ser comum aos dois conjuntos. Por isso, só iremos destacar uma determinada região nos diagramas dos conjuntos A e B, se esta for comum aos dois, como mostra a imagem abaixo nos 3 casos que revisamos no início do texto:

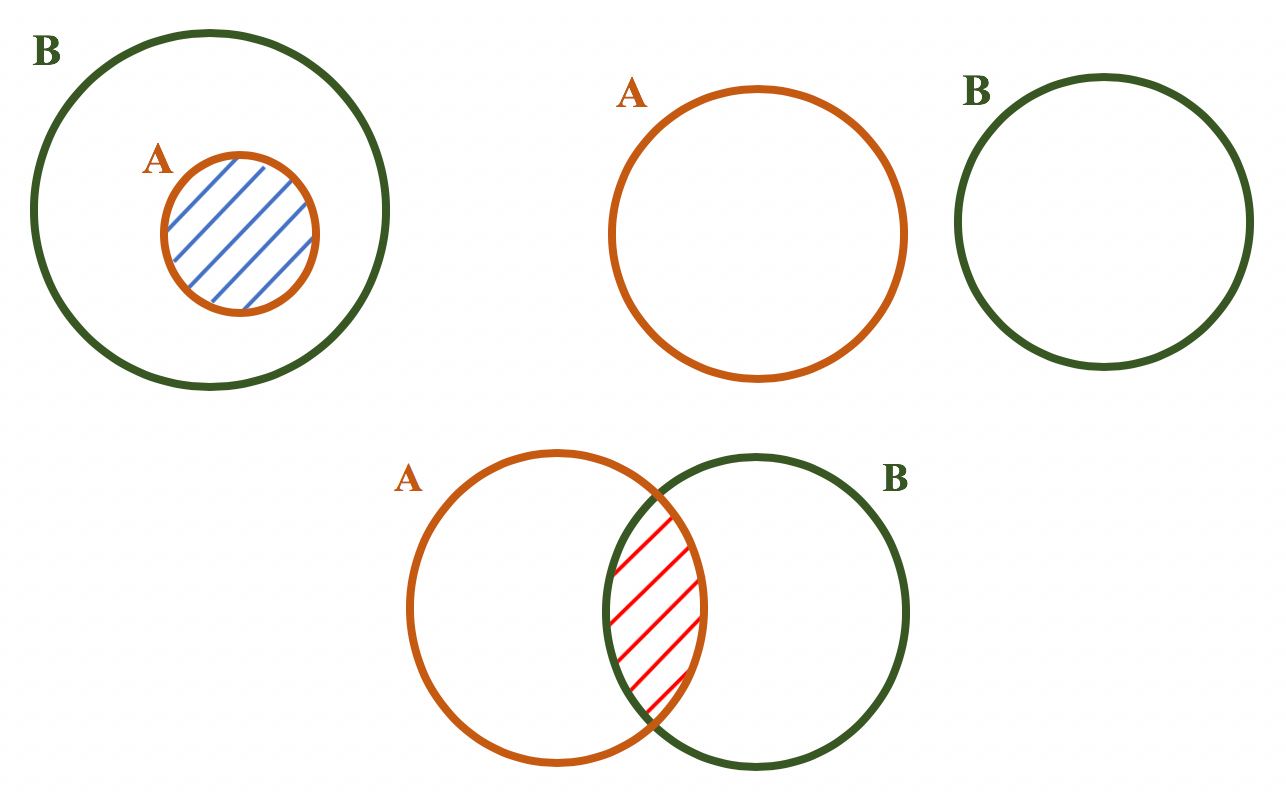
Reparem que quando dois conjuntos são disjuntos, não há elementos em comum entre eles. Por esse motivo, também não há área comum entre os diagramas. Isso só pode significar que a intersecção entre dois conjuntos disjuntos é igual ao conjunto vazio.

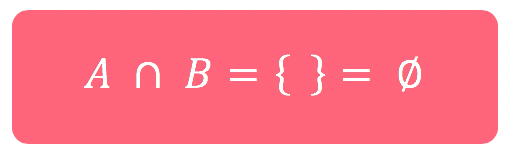
Certo, pessoal? Sendo assim, antes de partirmos para os famosos exercícios resolvidos, podemos aproveitar para dar uma olhada em algumas propriedades muito interessantes. Sigam comigo!

 

4. PROPRIEDADES DA UNIÃO E DA INTERSECÇÃO

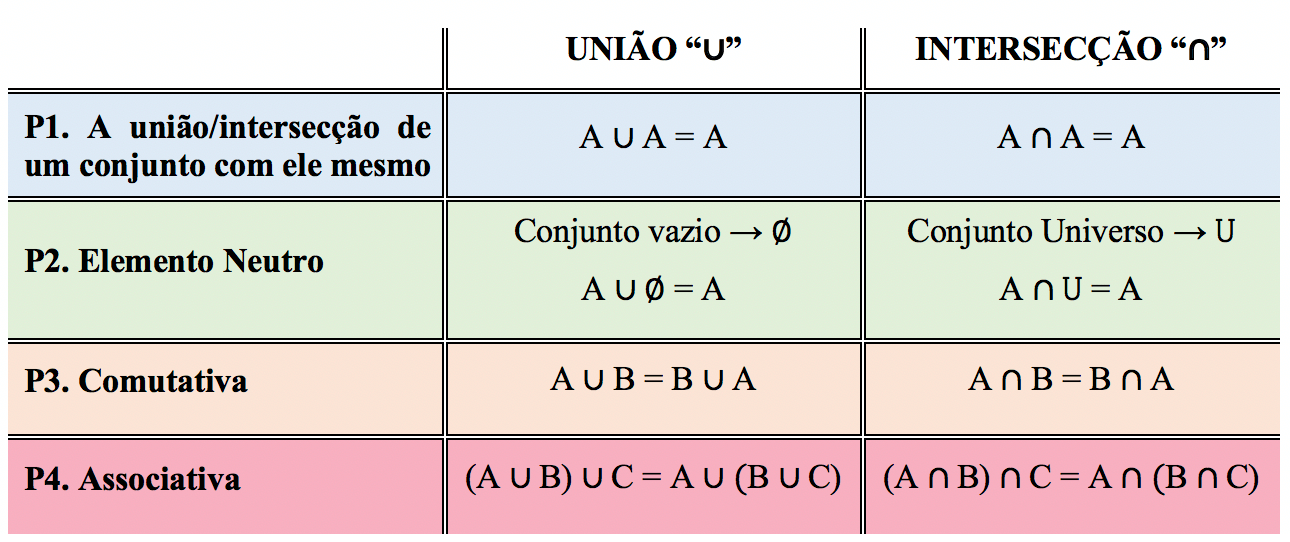
Agora que já conhecemos todas as propriedades da união e da intersecção, vamos conversar um pouco sobre cada uma delas. Reparem primeiramente na propriedade 1: tanto a união quanto a intersecção entre dois conjuntos A iguais, resulta, claramente, no próprio conjunto A.

Já quando se fala na propriedade 2, as coisas são diferentes para união e para a intersecção. Algo que é neutro, é definido como algo imparcial, indiferente, que não se envolve ou se compromete. Para ficar ainda mais claro, podemos pensar aqui em algo que não faz diferença ou que não causa mudança.

É por isso que o conjunto vazio é o elemento neutro da união e que o conjunto universo é o elemento neutro da intersecção. Quando um conjunto A, que possui uma série de elementos, une-se a um conjunto que não possui elemento algum, é obvio que prevalecerão os elementos do próprio conjunto A. Já quando há a intersecção entre um certo conjunto A, que possui determinados elementos, e um conjunto ao qual pertencem todos os números existentes, é claro que irão prevalecer os elementos comuns a ambos os conjuntos, que são os próprios elementos do conjunto A.

Louco, não é? Mas não se preocupem, as propriedades 3 e 4 são um pouquinho mais simples. Comutar, significa mudar, ou realizar a troca entre algo. Por isso, a propriedade comutativa nos informa que não importa se a ordem dos conjuntos A e B for alterada na hora de realizar a união ou a intersecção dos mesmos: o resultado será o mesmo!

E finalmente, resta-nos compreender que associar alguns elementos significa reuni-los ou agrupá-los. A propriedade 4, chamada de associativa, nos mostra que é possível associar de maneiras diferentes a união e a intersecção de diversos conjuntos, e o resultado será igual para todas as associações realizadas.

 

 5. EXERCÍCIOS RESOLVIDOS

É chegada a hora de aplicarmos tudo o que aprendemos hoje resolvendo alguns exercícios. Acompanhem comigo!

 

Encontre o conjunto união e o conjunto intersecção de A e B, nos casos abaixo:

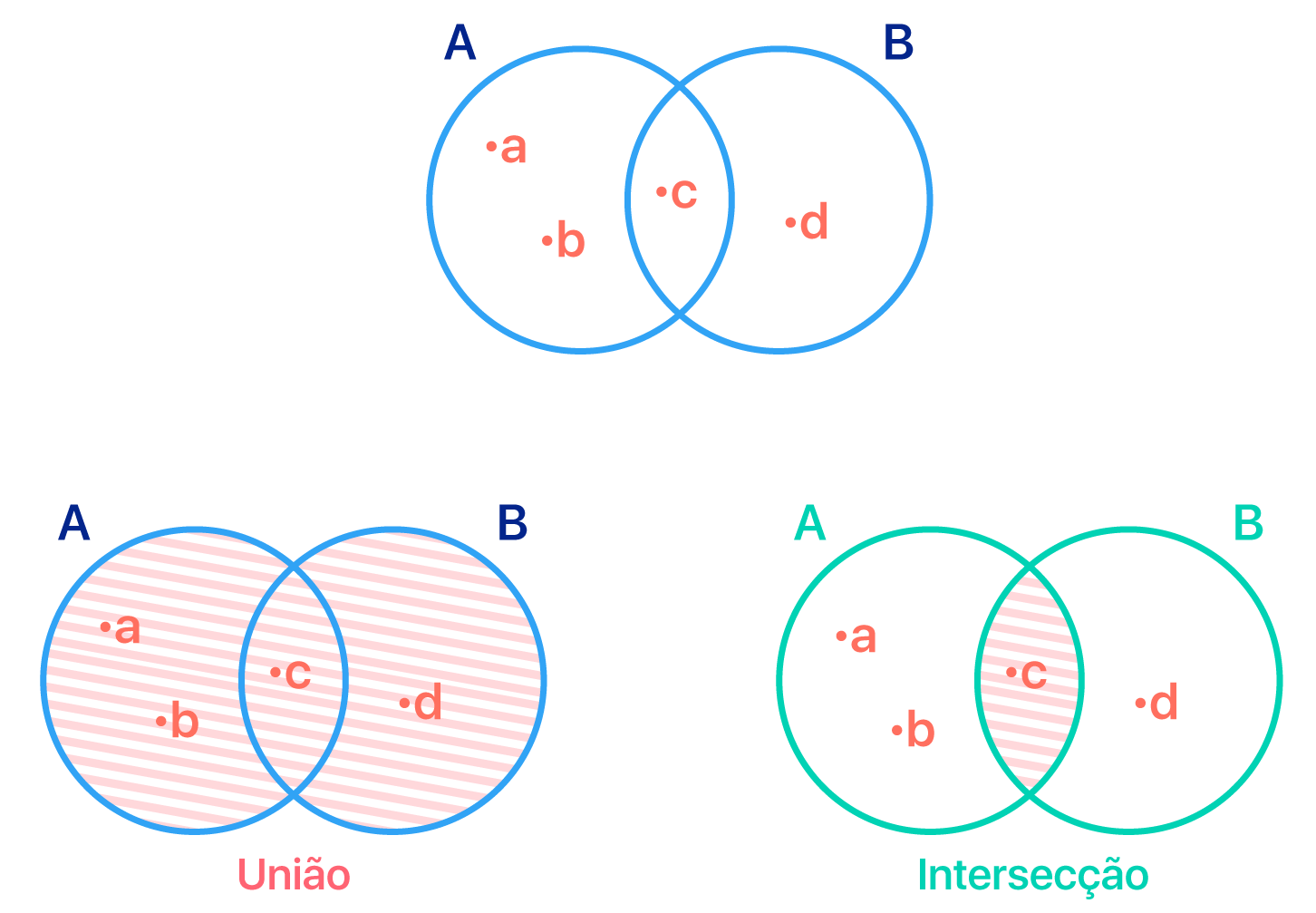
a) A = {a, b, c} e B = {c, d}

Reparem que o conjunto A é formado pelos elementos a, b, e c. Enquanto isso, o conjunto B é formado pelos elementos c e d. Para encontrar a união de A e B, basta copiarmos todos os elementos do conjunto A e todos os elementos do conjunto B. Caso houverem elementos em comum, não é necessário copiá-los duas vezes, de forma que:

A ∪ B = {a, b, c, d}

Para encontrar a intersecção de A e B, basta procurarmos pelos elementos em comum entre os dois conjuntos. Vejam que nesse caso, apenas o elemento c é comum a ambos os conjunto. Assim, temos que a intersecção de A e B é um conjunto unitário:

A ∩ B = {c}

Realizar a representação na forma de diagrama dos dois conjuntos pode ajudar, e muito, a obtermos os conjuntos união e intersecção que estamos procurando. Abaixo, segue a representação em diagrama dos conjuntos A e B. Na sequência, vocês verão as regiões destacadas que representam a união e a intersecção entre os dois conjuntos.

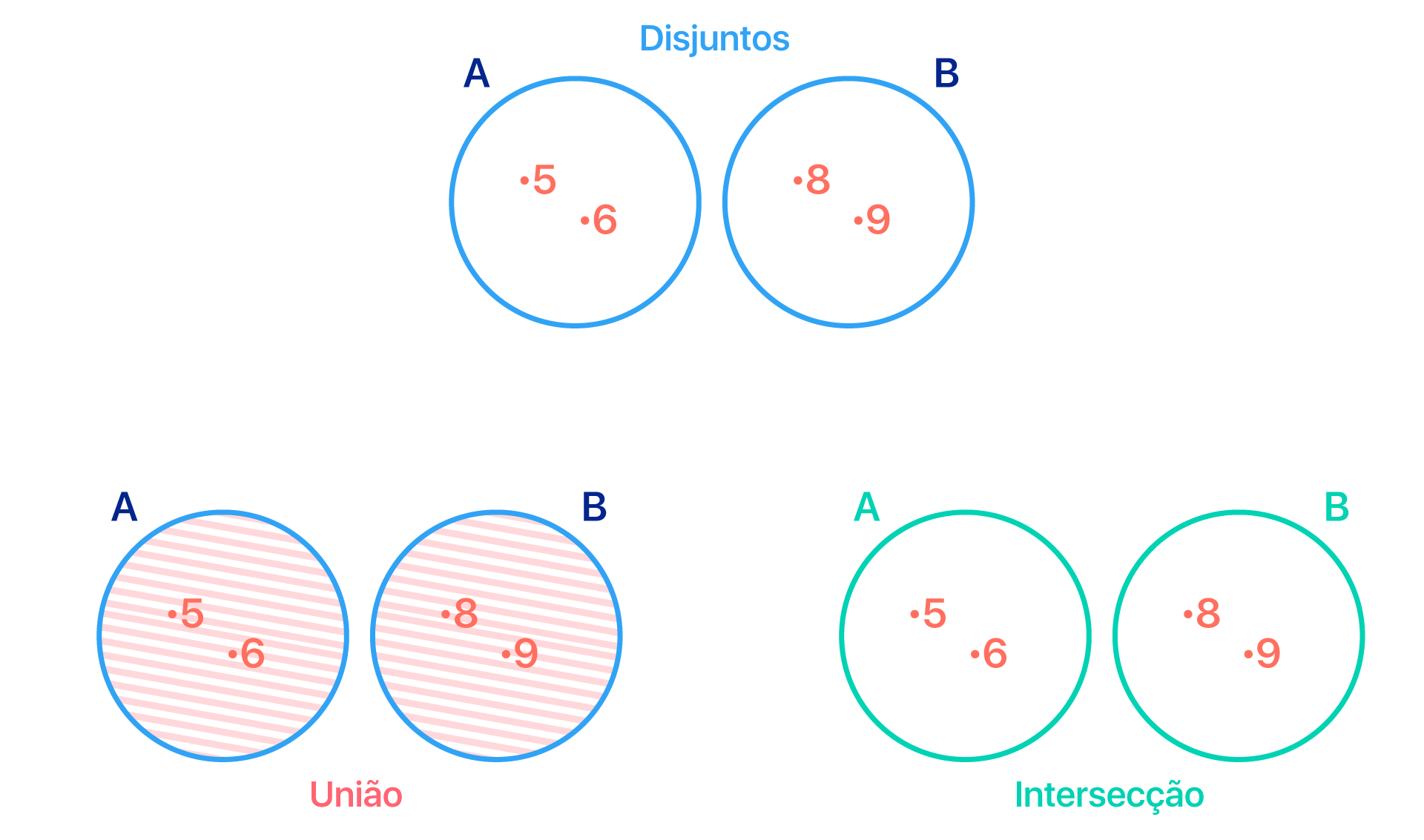
b) A = {5, 6} e B = {8, 9}

Neste caso, o conjunto A possui os elementos 5 e 6. Já o conjunto B possui os elementos 8 e 9. Assim, a união de A e B fica fácil, não é mesmo? Copiamos os elementos que pertencem ao conjunto A e também os elementos que pertencem ao conjunto B. Se houverem elementos em comum, não é necessário repeti-los.

A ∪ B = {5, 6, 8, 9}

 

Quando A e B são disjuntos …

Só que a verdade é que nessa questão não existem elementos em comum entre os conjuntos A e B. Por isso, podemos afirmar que A e B são conjuntos disjuntos e que a intersecção entre eles resulta no conjunto vazio.

A ∩ B = { }

É claro que não podemos deixar de representar os conjuntos deste exemplo em forma de diagrama. Por isso, deem uma olhada na imagem abaixo antes de seguir com o texto.

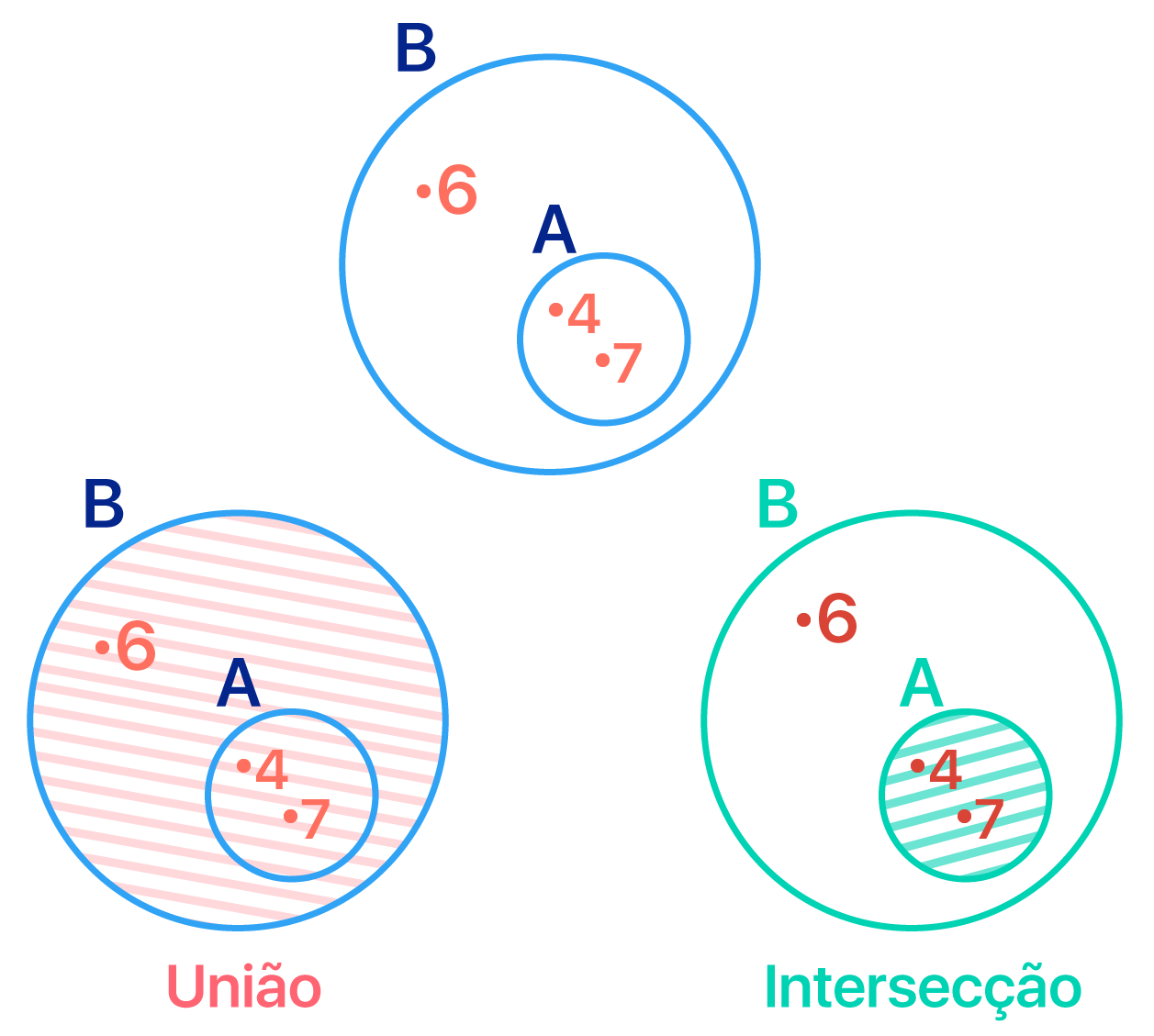
c) A = {4, 7} e B = {4, 6, 7}

Observem que os elementos do conjunto A são os números 4 e 7. Já os elementos do conjunto B são os números 4, 6 e 7. Parece que tem algo parecido aí, não é mesmo? É claro que tem: todos os elementos do conjunto A também pertencem ao conjunto B, e portanto pode-se dizer que A é subconjunto de B. Assim, é evidente que a união de A e B, e a intersecção de A e B, são os conjuntos descritos abaixo:

A ∪ B = {4, 6, 7}

A ∩ B = A = {4, 7}

A representação em forma de diagrama dos conjuntos A e B deste caso pode ser vista na imagem abaixo. Além disso, é possível acompanhar o destaque que representa a união e a intersecção entre os dois conjuntos.

 

Finalizando com orientações importantes!

Assim, concluímos mais um texto! Espero que ele tenha sido bem proveitoso para os estudos de vocês, e que os exemplos que resolvemos possam lhes ajudar a solucionar outras situações matemáticas que surgirem! É claro que em anexo fica o vídeo que complementa o assunto. Deem uma olhadinha nele, nos demais posts do blog, e se desejarem, façam seus comentários!

Gostou deste conteúdo? Clique aqui para saber como a Plataforma do Professor Ferretto funciona!

Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da Plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!

Um abraço e até o próximo texto!