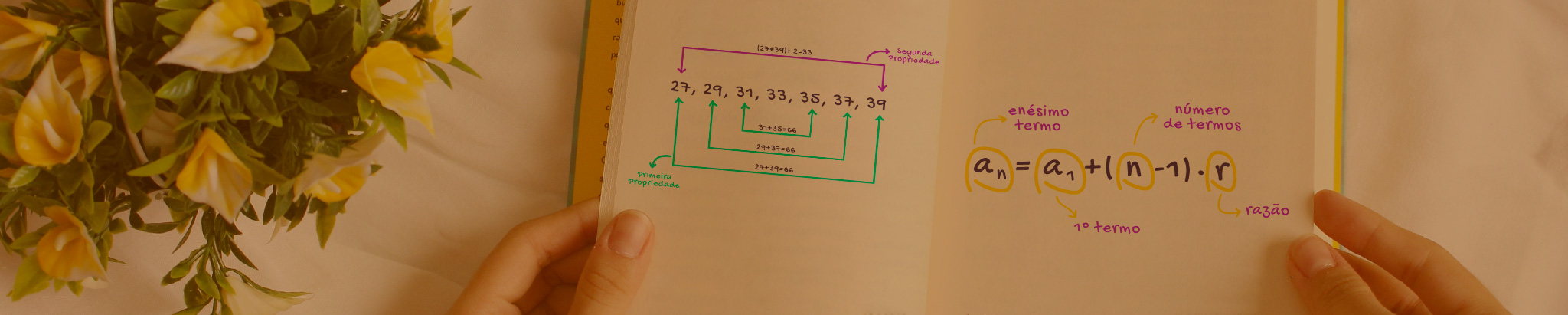
INTERPOLAÇÃO DE MEIOS ARITMÉTICOS
10/08/2018
Olá pessoal, tudo bem?
Só de olhar o título do nosso texto de hoje, vocês saberiam dizer o que estamos prestes a estudar? Sim? Não? Bom, então eu vou dar uma pista: o assunto de hoje tem a ver com uma sequência numérica muito conhecida, a progressão aritmética! Interpolar meios aritméticos, significa colocar uma série de termos entre dois números dados, de tal forma que a sequência gerada seja uma PA!
Pois bem, parece que o conteúdo é mais simples do que a sua própria denominação. Isso é verdade! Agora, poderia não ser tão simples assim resolver aquelas questões do ENEM e dos vestibulares que tratam do assunto, se vocês nunca o tivessem estudado! Pessoal, se vocês desejam realizar alguma dessas provas e ter sucesso, não dá para deixar de estudar nenhum conteúdo da matemática do ensino médio! E uma ótima maneira de garantir que tudo seja visto com um alto rendimento é assinando a plataforma do Professor Ferretto! O curso de matemática do Ferretto é repleto de videoaulas, de exercícios do ENEM e dos vestibulares disponíveis para resolução, além de simulados, e até mesmo aulas de física. É isso mesmo! Ficaram curiosos para saber como funciona? Então acessem o site e confiram todos os detalhes!
Depois dessa dica muito valiosa, é hora de iniciarmos nossos estudos! Nossa tarefa de hoje, é descobrir como é possível colocar uma série de termos entre dois números dados, de tal forma que a sequência gerada seja uma PA. Então, digamos que a sequência que devemos encontrar seja dada nesta forma:
(2, __, __, __,10)
Podemos ver na sequência acima, que são dados dois números: 2 e 10. Entre eles temos 3 espaços, o que sugere que precisamos colocar 3 termos ou 3 meios aritméticos ali de forma que a sequência se torne uma PA. Mas como é possível construir uma progressão aritmética sem saber como ela é formada, ou seja, sem conhecer a definição de uma PA?
Uma PA é uma sequência em que cada termo, a partir do segundo, é a soma do anterior com uma constante r dada.
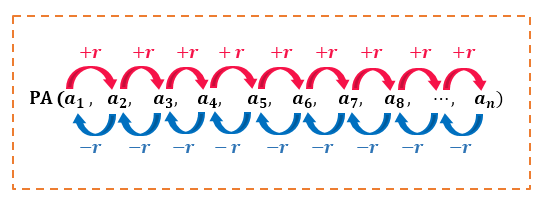
Observando o quadro, também podemos dizer que uma PA é uma sequência em que qualquer termo, que não seja o último, pode ser obtido através da subtração da razão r do seu termo sucessor, como mostram os exemplos:

Mas o fato mais interessante, é que é possível encontrar o valor de qualquer termo de uma PA, conhecendo apenas o valor de algum outro termo desta progressão, e a sua razão r. Para fazer isso, basta utilizarmos a fórmula do termo geral de uma PA, essa que aparece logo abaixo:
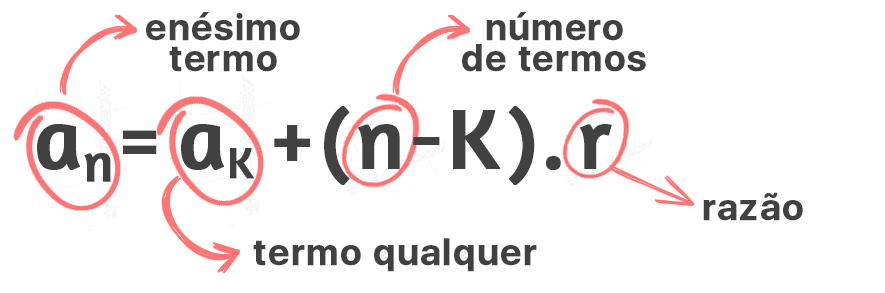
Essa fórmula nos permite encontrar o valor do enésimo termo de uma progressão aritmética, o an, com base na razão r da PA, e no valor de qualquer outro termo da sequência, que pode estar a esquerda, a direita, e mesmo muito distante de an. É só observar os saltos que a razão dá na sequência, para a direita ou para a esquerda, ou ainda, subtrair os índices dos termos. Querem ver como funciona? Digamos, por exemplo, que o nosso objetivo seja encontrar o valor do termo a9 de uma PA, conhecendo apenas o valor do termo a2 e a sua razão r. Subtraindo o número 2, do número 9, nós temos o valor 7, e portanto, nossa fórmula do termo geral da PA ficaria assim:
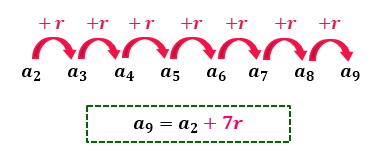
E se o nosso objetivo fosse encontrar o valor do termo a3 de uma PA, conhecendo apenas o valor do termo a8 e a sua razão r? Nesse caso, subtraindo 8 de 3, nós temos o resultado –5, e nossa fórmula do termo geral da PA ficaria assim:
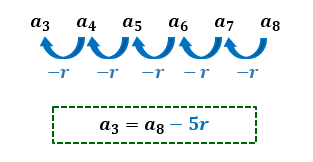

Pois bem pessoal, para entendermos porque estamos revisando tanto a fórmula do termo geral da PA, nós vamos observar novamente a sequência apresentada lá no início do texto:
(2, __, __, __,10)
Vejam que dessa sequência, nós só conhecemos os valores do primeiro e do último termo, a1 e an, respectivamente. Mas, como temos 2 termos conhecidos, e 3 termos ou meios aritméticos para encontrar, já podemos afirmar que o último termo da sequência é, na verdade, o seu 5º termo. Sendo assim, podemos dizer mais precisamente, que conhecemos os valores numéricos dos termos a1 e a5, e precisamos encontrar os valores de a2, a3 e a4.
(2, __, __, __,10)
(a1, a2, a3, a4, a5)
Até aí tudo certo, não é mesmo? Mas vocês não sentiram falta de nenhuma outra grandeza? Pois é, nós não conhecemos a razão r que torna essa sequência uma progressão aritmética!!! Então pessoal, é por isso que nós temos falado tanto na fórmula do termo geral da PA, porque na medida em que conhecemos dois termos quaisquer de uma progressão aritmética, mesmo que distantes um do outro, como a1 e a5, por exemplo, essa fórmula nos permite encontrar a razão r dessa progressão.
Para interpolar os mais diversos meios aritméticos, é preciso, sempre, conhecer a razão r que envolve a sequência de que se está tratando!
Assim, podemos montar a seguinte equação para o caso:
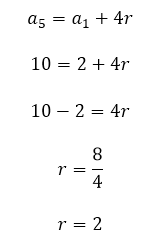
Agora, já é possível determinar os 3 meios aritméticos da sequência do exemplo, de forma que ela seja considerada uma PA, como mostra a figura abaixo:
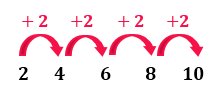
Bem fácil, não é mesmo? Então, aos nos depararmos com um caso em que se pede a interpolação dos mais diversos meios aritméticos, basta utilizarmos a fórmula do termo geral da PA para encontrarmos a razão r da sequência, tudo com base no primeiro e no último termo da mesma. De posse da razão da progressão, obter os meios aritméticos desejados se torna muito simples.
Para mostrar que tudo o que eu disse é a mais pura verdade, nós vamos resolver agora três exercícios muito interessantes. Vem comigo aqui!
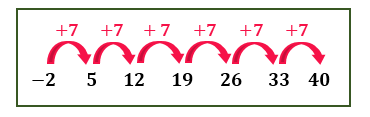
1. Interpolar 5 meios aritméticos entre -2 e 40.
Pessoal, antes de mais nada, é muito importante vocês notarem no enunciado dos exercícios, que sempre são dados os valores do primeiro e do último termo da sequência em que se deseja realizar a interpolação, e também, é claro, o número de meios aritméticos que deverão ser inseridos para que uma PA seja formada. Isso nos permite concluir, que o número de termos n da sequência dada neste caso é 7, já que conhecemos 2 termos, e iremos interpolar mais 5 termos entre eles. Para ficar mais claro, escrevam a sequência sempre, deixando os espaços necessários para os termos que serão interpolados:
(– 2, __, __, __, __, __, 40)
(a1, a2, a3, a4, a5, a6, a7)
Desta forma, nós conseguimos perceber que de a1 até a7 existem 6 saltos da razão r. Por isso, é possível dizer que a7 é igual a a1 acrescido de 6 razões:
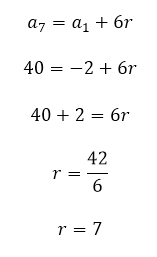
2. Quando inserimos 10 meios aritméticos entre 2 e 79, qual é a razão da PA obtida?
Se devem ser inseridos 10 meios aritméticos entre 2 e 79, é fato que a PA que será formada por essa sequência terá 12 termos ao todo, ou seja n = 12. Então, vamos escrever essa sequência com os espaços necessários a todos os meios aritméticos pedidos, para em seguida, montar a equação correta que nos permita encontrar a razão para o caso:
(2, __, __, __, __, __, __, __, __, __, __, 79)
(a1, a2, a3, a4, a5, a6, a7, a8, a9, a10, a11, a12)
Observem que de a1 até a12 existem 11 saltos na razão r. Assim, é fato que a12 é igual a a1 acrescido de 11 razões:
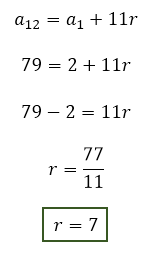
3. Inscrevendo-se nove meios aritméticos entre 15 e 45, qual é o sexto termo da PA?
Novamente, temos o valor do primeiro e do último termo da sequência que deverá ser formada, respectivamente, 15 e 45. E se entre eles devem ser inseridos 9 meios aritméticos, isso significa que a progressão aritmética terá um total de 11 termos, n = 11. Então é claro que o último termo da PA é, na verdade, o seu 11º termo, e que a11 é igual a a1 acrescido de 10 razões.
(15, __, __, __, __, __, __, __, __, __, 45)
(a1, a2, a3, a4, a5, a6, a7, a8, a9, a10, a11)
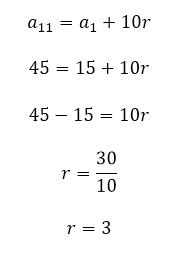
Contudo, nesse caso, nem mesmo se fala na sequência que será formada quando esses 9 termos forem inseridos entre 15 e 45, através da razão r = 3. Pede-se, na verdade, o valor do 6º termo da PA, o a6. Bom, se de a1 até a11, temos 10 saltos da razão r, de a1 até a6, tem-se apenas 5 saltos da razão. Assim, a6 é igual a a1 acrescido de 5 razões.
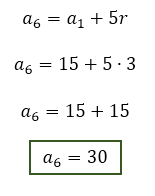
Tranquilo, não é mesmo? Então, caso vocês não tenham percebido, aí vai uma dica bem importante! Praticamente tudo, em PA, se resume a duas fórmulas muito interessantes: a fórmula do termo geral de uma PA e a fórmula da soma dos termos de uma PA. Se vocês conhecerem direitinho essas duas fórmulas, é muito provável que não haja erro em qualquer questão que trate do assunto!
E eu, claro, vou precisar encerrar o texto de hoje por aqui! Espero que vocês tenham gostado da abordagem do assunto, e que o texto tenha sido muito proveitoso para os seus estudos! Mas antes de encerrar mesmo, informo que não dá para deixar de ver o vídeo que está em anexo. Lá vocês encontram a resolução de um exercício clássico da progressão aritmética, e que tem tudo a ver com a interpolação: uma questão de múltiplos! Tenho certeza que essa resolução irá contribuir muito para o conhecimento de vocês!
Abração e uma ótima semana de estudos!