
Os assuntos de Matemática que mais caem no ENEM vivem na sua cabeça, mas a nota não sai do lugar?...
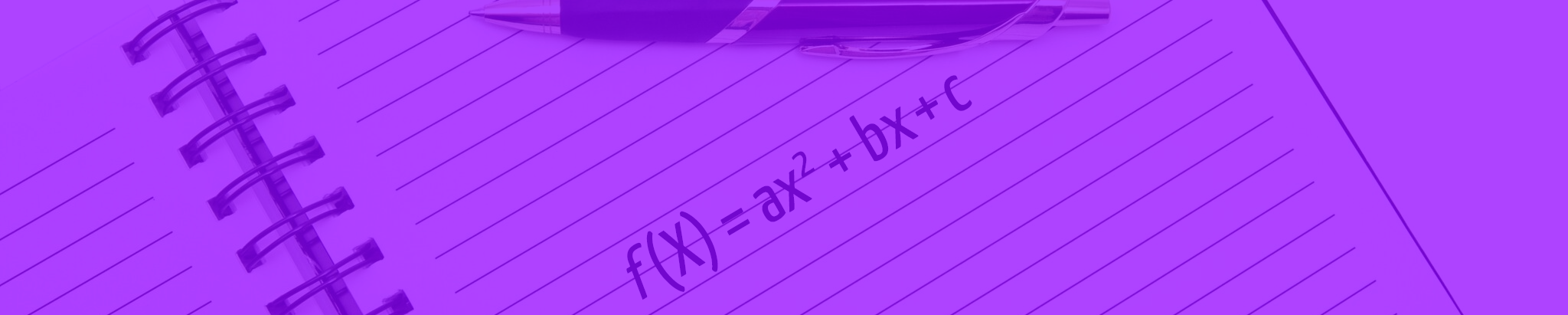
A função quadrática, ou função polinomial do 2º grau, é a conhecida f(x) = ax²+bx+c. Você verá neste texto tudo sobre a, b, e c e sobre o gráfico dessa função. Vem comigo aqui!
Olá pessoal! Como vão vocês?
O lançamento de projéteis, ou de uma bola na cesta de basquete, são algumas das inúmeras aplicações práticas da função quadrática, também conhecida como função polinomial do segundo grau. Isso sempre irá acontecer quando determinado fenômeno apresentar um comportamento parabólico, ou seja, quando puder ser representado por uma parábola, que nada mais é do que o gráfico característico desta função.
O fato é que é praticamente impossível aplicar a função quadrática com maestria sem conhecer os seus conceitos mais simples. Por isso, o texto de hoje é voltado para quem nunca ouviu falar da função do 2º grau, ou sabe pouco sobre ela, mas deseja adquirir o conhecimento necessário para aplicar os seus conceitos nas provas do ENEM, dos vestibulares, e mesmo em outras finalidades mais complexas!
É pessoal, na maioria das vezes, quando deixamos os conceitos mais simples de lado, eles costumam fazer falta quando precisamos entender os conteúdos mais exigentes. E é claro que na matemática não podia ser diferente. Mas não se preocupem, é por isso que a plataforma do Professor Ferretto existe! Lá vocês encontram um curso de matemática completo e 100% online, onde toda a matemática do ensino médio é abordada com foco na melhor preparação para o ENEM, e para os tradicionais vestibulares do país! Acessem o site e conheçam todos os benefícios do curso!
E aí, vamos começar? Fiquem agora com a definição da função quadrática!
1. DEFINIÇÃO DA FUNÇÃO DO 2º GRAU

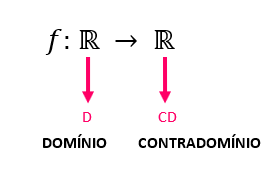
Uma função f: ℝ→ℝ chama-se quadrática quando existem números reais a, b, c, com a ≠ 0, tal que f(x) = ax2 + bx + c para todo x ∈ ℝ.
Primeiramente, é importante repararmos que toda função quadrática é dita como uma função f: ℝ→ℝ. Essa representação costuma parecer confusa, mas a informação que ela nos traz é muito valiosa: a função f de reais em reais, é uma função cujo o domínio ou conjunto de partida, e o contradomínio ou conjunto de chegada pertencem ao conjunto dos números reais. Isso significa que números positivos, negativos, frações, dízimas periódicas, raízes não exatas e todo e qualquer número real pode fazer parte do domínio e do contradomínio desta função, sem que haja qualquer restrição.
Além disso, a definição da função quadrática nos mostra que sua forma característica é f(x) = ax2 + bx + c. Mas toda e qualquer função matemática pode ser representada por f(x) ou por y, por isso, a expressão y = ax2 + bx + c, também é considerada uma função do 2º grau.

E se vocês observaram a expressão da função quadrática, mas não a associaram ao seu nome, saibam que o termo 2º grau tem tudo a ver com o grau do polinômio ax2 + bx + c, expresso pelo maior expoente da variável x. É por isso que a definição nos informa, que o coeficiente a que acompanha o termo x2, deve ser necessariamente diferente de zero (a ≠ 0), porque é esse termo que caracteriza a função quadrática. Imaginem só, se a for zero, o termo ax2 deixará de existir, restando apenas a expressão “bx + c”. Essa expressão representa claramente outra função matemática, a função polinomial do 1º grau, também chamada de função afim.
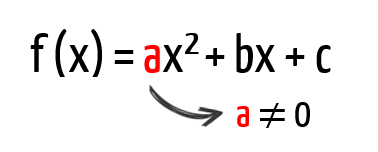
Felizmente, não há restrição alguma quanto aos valores numéricos dos demais coeficientes da função do 2º grau, no caso, b e c. Vocês verão ao longo dos estudos, que existirão algumas funções quadráticas onde b é de valor zero, outras em que c é de valor zero, e ainda, certas funções onde ambos valem zero. Mas não há problema algum nisso. O importante é lembrar sempre do seguinte: a é o coeficiente que pertence ao termo x2, b é o coeficiente que acompanha o termo x, e c é considerado o termo independente da função quadrática, pois não acompanha variável alguma.
Bom, chegou a hora de darmos uma folga para a teoria, e encontrarmos os coeficientes a, b, e c de algumas funções do segundo grau. Vem comigo aqui!
1. f(x) = 3x2 – 4x + 2
f(x) = 3x2 – 4x + 2
a = 3; b = – 4; c = 2
Reparem que neste exemplo, havia um sinal negativo na expressão. Mas a forma característica da função quadrática f(x) = ax2 + bx + c não possui sinal negativo algum. Assim, todo sinal negativo que surge em uma expressão do 2º grau sempre irá pertencer ao seu respectivo coeficiente, e por isso, o valor do coeficiente b, aqui, foi –4.
2. f(x) = x2 + 3x
f(x) = x2 + 3x
a = 1; b = 3; c = 0
Vejam que neste segundo caso, todos os termos são acompanhados pela variável x. Isso nos mostra que não há termo independente nesta função, e portanto o coeficiente c vale zero. Outro detalhe interessante neste exemplo é o valor do coeficiente a. Sempre que os termos x2 e x estiverem “sozinhos”, significa que os seus coeficientes valem “1”.
3. y = – x2 – 5
y = – x2 – 5
a = –1; b = 0; c = – 5
Como afirmamos no texto, uma função quadrática pode ser representada tanto por f(x) quanto por y. Mas neste caso em específico, não há termo algum que esteja acompanhado somente pela variável x, o que justifica o fato do coeficiente b valer zero.
4. y = –2x2
y = – 2x2
a = –2; b = 0; c = 0
A função quadrática apresentada acima, é um dos diversos exemplos de função do 2º grau que possuem apenas o coeficiente a. Mas nós sabemos que isso é mais que o suficiente para que a mesma seja classificada como função de tal grau, não é mesmo?
Portanto, já que vocês já sabem tudo sobre os coeficientes da função quadrática, chegou a hora de avançarmos um pouquinho. Vamos descobrir agora, como é possível representar graficamente as mais diversas funções do segundo grau existentes. Acompanhem comigo!
2. CONSTRUINDO O GRÁFICO DA FUNÇÃO QUADRÁTICA
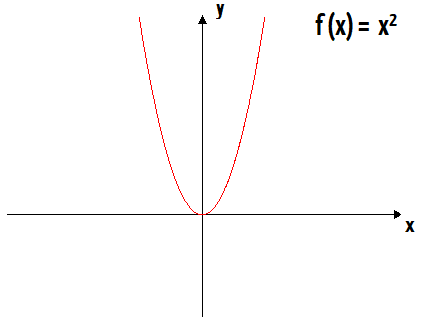
O gráfico de uma função quadrática f (x) = ax2 + bx + c, com a ≠ 0, é uma curva chamada parábola.
Exatamente! O gráfico característico da função quadrática é uma parábola, como aquela que aparece na figura logo acima. O fato, é que existe um método muito comum que nos permite construir gráficos como esse e de quaisquer outras funções matemáticas: basta adotar uma série de valores para x e aplica-los à função f (x) = ax2 + bx + c, de forma a obter os seus respectivos valores em y. Feito isso, é só montar uma tabelinha com todos os pares ordenados (x, y) encontrados, e realizar a sua representação gráfica no plano cartesiano.
Querem ver como funciona? Vamos construir agora, o gráfico da função f (x) = x2 – 1.
O primeiro passo, como vimos no texto, é adotar uma série de valores de x que serão as coordenadas do eixo das abscissas. Sendo assim, adotaremos aqui os valores – 2, – 1, 0, 1 e 2. Agora resta-nos substituir todos eles na função f (x) dada no enunciado. Os resultados dessas operações, serão as coordenadas em y, ou do eixo das ordenadas, da função f (x) = x2 – 1. Vamos lá então:
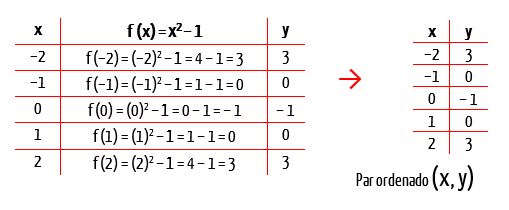
Agora que temos alguns pontos em mãos, já podemos representa-los no plano cartesiano. Vejam só:
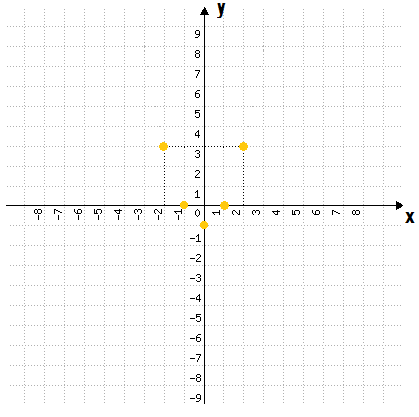
A forma como esses pontos estão localizados no plano, já nos dá uma ideia de como é o comportamento da função como um todo. Mas se vocês desejarem tornar a representação ainda mais precisa, podem calcular mais alguns pontos, com valores de x tais como –3, –1,5, 1,5 e 3.
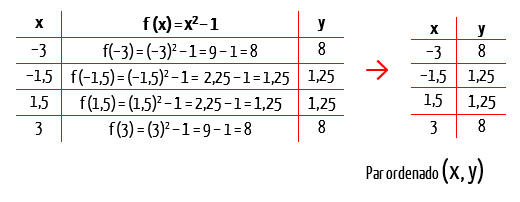
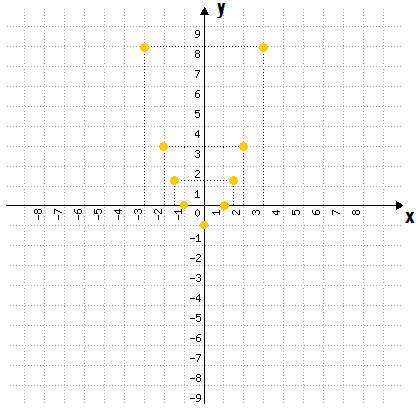
Já ficou bem mais interessante, não é mesmo? Pois bem, na medida em que escolhermos mais uma série de valores de x, e calcularmos os seus respectivos valores em y, teremos outros infinitos pontos nesta curva, que darão ainda mais forma ao gráfico da função f (x) = x2 – 1. Mas preencher todos os pontos desta curva seria impossível, pelo menos em pouco tempo. Por isso a ideia é ligar todos os pontos que já encontramos, formando a curva apresentada na imagem abaixo:
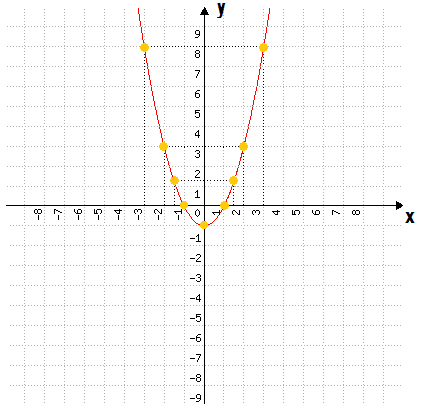
Incrível, não é mesmo? Só não é tão incrível calcular essa infinidade de pontos, vocês não acham? O fato é que nós fizemos aqui uma representação bastante precisa da função quadrática, mas não é necessário fazer isso sempre: geralmente dois ou três pontos são suficientes para definir a forma da função do segundo grau. O problema é que assim, aleatoriamente, nem sempre conseguimos acertar essas duas ou três coordenadas (x, y) que nos permitem construir um gráfico facilmente. Por isso, precisamos de um método que nos permita calcular os pontos certos, que proporcionam uma representação simples e rápida!
Mas não se preocupem com isso, porque alguém já desvendou uma solução para o caso. É possível construir um gráfico de forma ainda mais fácil, quando conhecemos o valor do vértice da parábola, sua concavidade, o valor de suas raízes, e claro a sua perfeita simetria. Vocês querem saber o que significam todos esses termos? Então deem uma olhada nos textos “Vértice da parábola, valor máximo ou mínimo da função quadrática” e “Quantidade de raízes reais da função quadrática”. Pronto, tudo que aprendemos aqui, aliado ao que vocês verão nesses textos, fará o conhecimento de vocês dar um salto rumo aquela nota alta desejada nas provas que irão fazer!
Certo, pessoal!? Não vai ter jeito, vou precisar encerrar o texto por aqui! Mas espero que esses conceitos, mesmo que simples, possam ter sido esclarecedores, lhes motivando a seguir engajados nos estudos! É claro que em anexo, fica o vídeo que aborda todo esse assunto. Não custa nada dar uma olhadinha nele, e complementar aquilo que, por ventura, possa não ter ficado tão claro.
Um abração a todos! Tenham ótimos estudos!
