Existe uma fórmula capaz de definir facilmente o número de elementos da união entre dois conjuntos A e B. Baseando-se nela, é possível obter uma segunda fórmula: a do número de elementos da união entre três conjuntos, A, B e C.

 

Olá, pessoal! Como vão vocês?

Estamos bastante acostumados a encontrar o conjunto união entre dois conjuntos A e B. Contudo, dificilmente nos preocupamos com o número, ou com a quantidade de elementos desse conjunto. Não parece, mas a verdade é que essa informação pode nos ajudar a resolver diversas questões do ENEM, e principalmente de vestibulares.

Por isso, aprenderemos no texto de hoje a fórmula do número de elementos da união entre 2 e 3 conjuntos. Faremos também alguns exemplos, para consolidar todo esse conhecimento. Quem está pensando em prestar vestibulares logo mais, terá de seguir comigo!

Beleza, pessoal? Então, é hora de iniciarmos os estudos. Vem comigo!

 

1. FÓRMULA DO NÚMERO DE ELEMENTOS DA UNIÃO ENTRE 2 CONJUNTOS

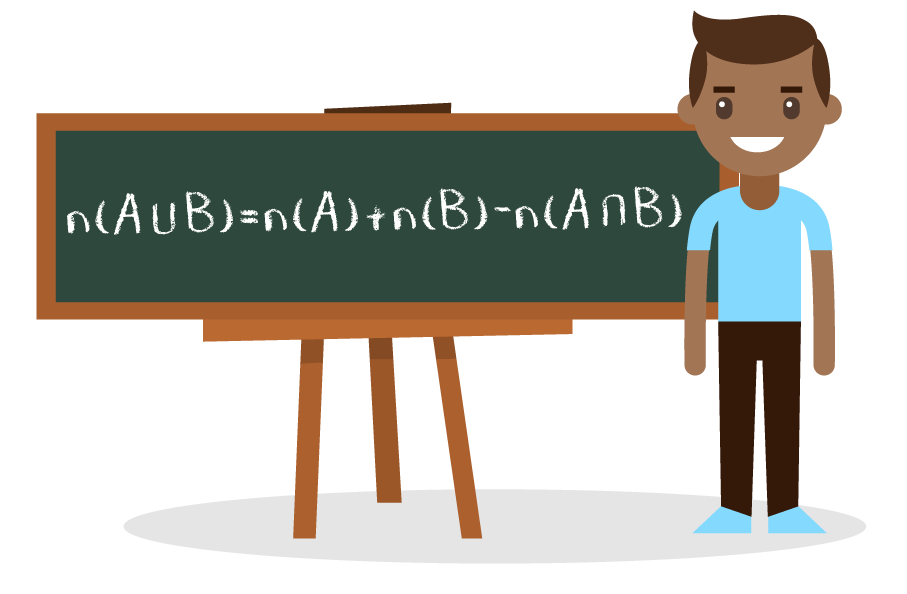
Então, o que acharam da fórmula apresentada na imagem acima? Eu sei, parece confuso determinar a quantidade de elementos do conjunto união entre os conjuntos A e B. Mas tenho certeza de que partindo de um exemplo, tudo ficará mais claro. Deem uma olhada nos conjuntos A e B descritos abaixo.

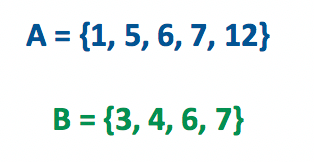
A união entre dois conjuntos A e B pode ser definida como o conjunto formado pelos elementos que pertencem a A ou a B, de acordo com o texto União e Intersecção. Isso significa que a união dos conjuntos A e B apresentados acima, é um conjunto formado pelos elementos que pertencem ou a A, ou a B, ou a ambos os conjuntos.

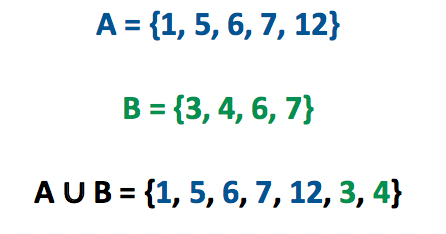
Vejam que para determinar o conjunto união entre A e B, nós copiamos todos os elementos de A, e depois copiamos todos os elementos de B. Mas como haviam dois elementos em comum entre os conjuntos (6 e 7), não houve a necessidade de copiá-los novamente. Quando os conjuntos são representados na forma de diagrama, fica ainda mais fácil determinar união entre eles.

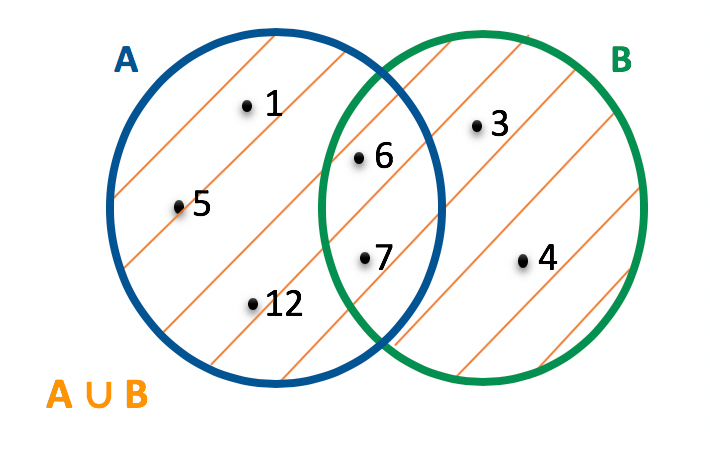
Claro! Neste caso, é só copiar todos os elementos dispostos no diagrama. Isso porque nessa forma de representação, os elementos comuns a ambos os conjuntos já ficam em evidência na região entrelaçada.

Bom, se os elementos que são comuns aos conjuntos A e B fazem diferença na hora de montarmos o conjunto união entre eles, é claro que também fazem diferença na hora de determinar o número de elementos deste conjunto, n (A ∪ B).

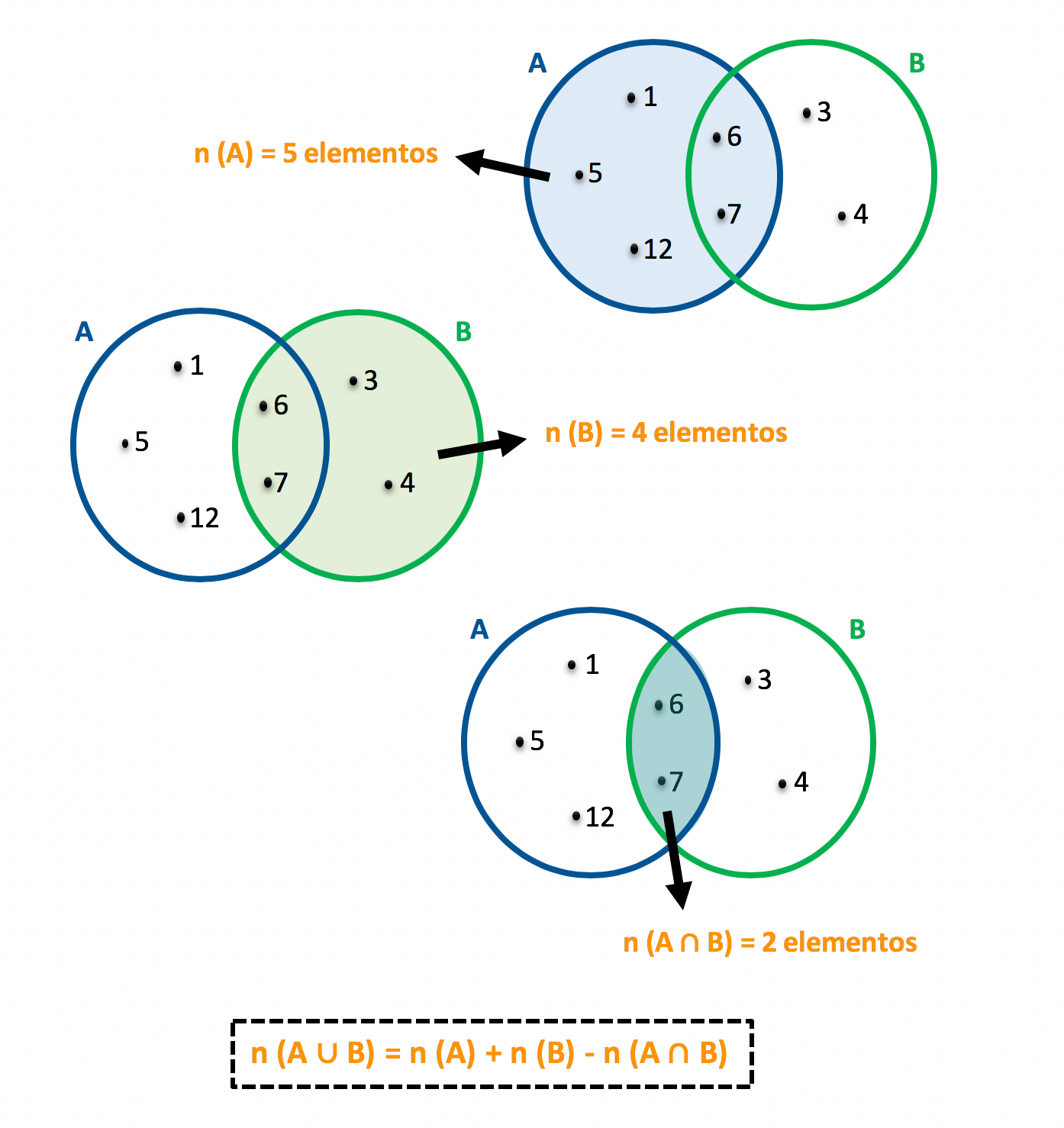
Assim faz todo o sentido, não é mesmo? Como os termos n(A) e n(B) contabilizam o número de elementos comuns a ambos os conjuntos, precisamos descontá-los uma vez, ou estaremos levando em conta elementos repetidos.

 

1.1 Aplicando a fórmula do número de elementos da união

Querem ver como é verdade? Contando os elementos do conjunto união que havíamos obtido, A ∪ B = {1, 5, 6, 7, 12, 3, 4}, é fato que este possui 7 elementos. Vamos usar a fórmula do número de elementos da união para ver se o resultado é equivalente.

n (A ∪ B) = n (A) + n (B) – n (A ∩ B)

n (A ∪ B) = 5 + 4 – 2

n (A ∪ B) = 7

E não é que deu certo? Aproveitaremos a deixa para desenvolver um novo exemplo!

 

Dados os conjuntos A = {1, 3, 5 ,7, 9} e B = {2, 3, 5, 7}, determine o número de elementos da união de A e B.

Observando rapidamente os conjuntos dispostos no enunciado, podemos concluir que:

• O conjunto A possui 5 elementos: 1, 3, 5, 7, e 9.
• O conjunto B possui 4 elementos: 2, 3, 5, e 7.
• Ambos os conjuntos possuem 3 elementos em comum: 3, 5 e 7, de forma que A ∩ B = {3, 5, 7}.

Assim, o número de elementos da união de A e B, é dado por:

n (A ∪ B) = n (A) + n (B) – n (A ∩ B)

n (A ∪ B) = 5 + 4 – 3

n (A ∪ B) = 6

Para provar que o resultado está correto, vamos encontrar o conjunto união de A e B. É possível perceber que ele realmente possui 6 elementos:

A ∪ B = {1, 2, 3, 5, 7, 9}

 

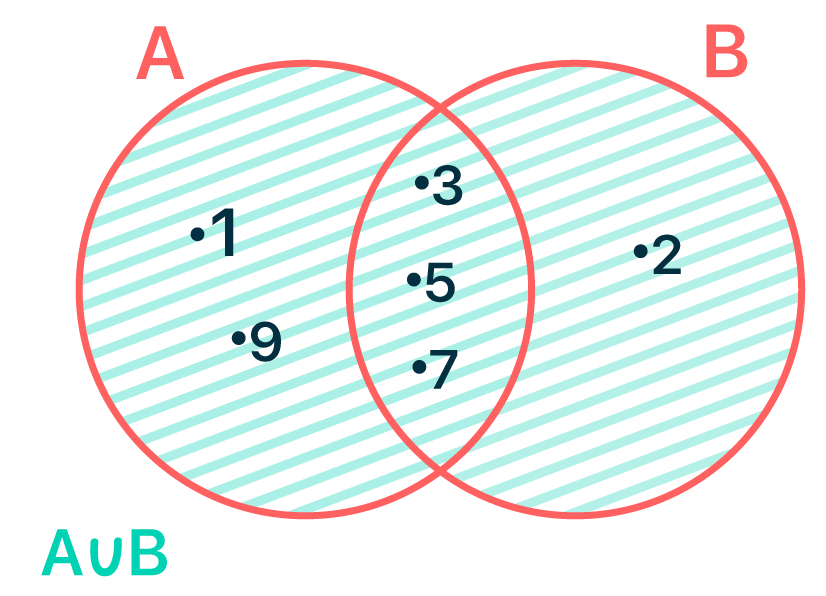
3. FÓRMULA DO NÚMERO DE ELEMENTOS DA UNIÃO ENTRE 2 CONJUNTOS DISJUNTOS

Sendo A e B dois conjuntos disjuntos, ou seja, dois conjuntos que não possuem elementos em comum, é fato que A ∩ B = ∅. Assim, o termo n (A ∩ B) da fórmula do número de elementos da união se torna nulo, ou igual a zero. Isso possibilita resumir a expressão que acabamos de conhecer.

Quando dois conjuntos A e B são disjuntos, o cálculo do número de elementos da união de A e B se resume a expressão n (A ∪ B) = n (A) + n (B).

Tranquilo, não é mesmo? Agora, para findarmos este texto com chave de ouro, vamos partir da mesma ideia aplicada ao número de elementos da união de dois conjuntos para deduzirmos a fórmula do número de elementos da união entre três conjuntos. A representação em forma de diagrama vai nos ajudar novamente. Vem comigo!

 

4. FÓRMULA DO NÚMERO DE ELEMENTOS DA UNIÃO ENTRE 3 CONJUNTOS

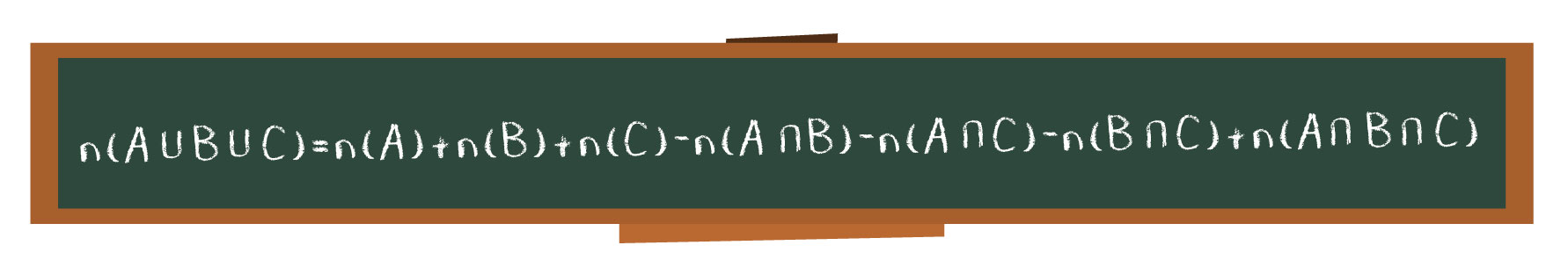
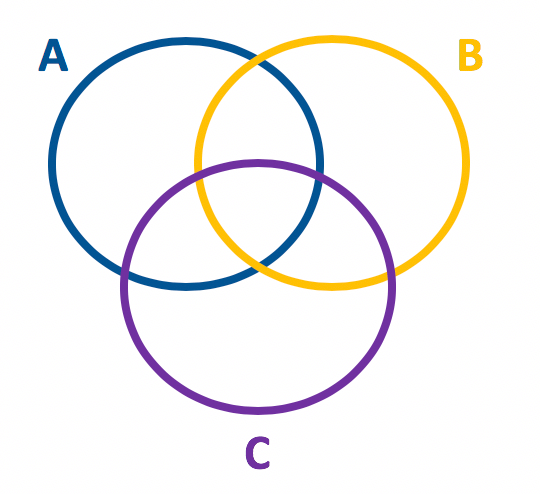
E aí, o que acharam do tamanho desta fórmula? Vamos começar nossa dedução partindo da representação em forma de diagrama de 3 conjuntos A, B e C. Pensaremos aqui em conjuntos que possuem apenas alguns elementos em comum, e por isso, seus diagramas poderão se entrelaçar.

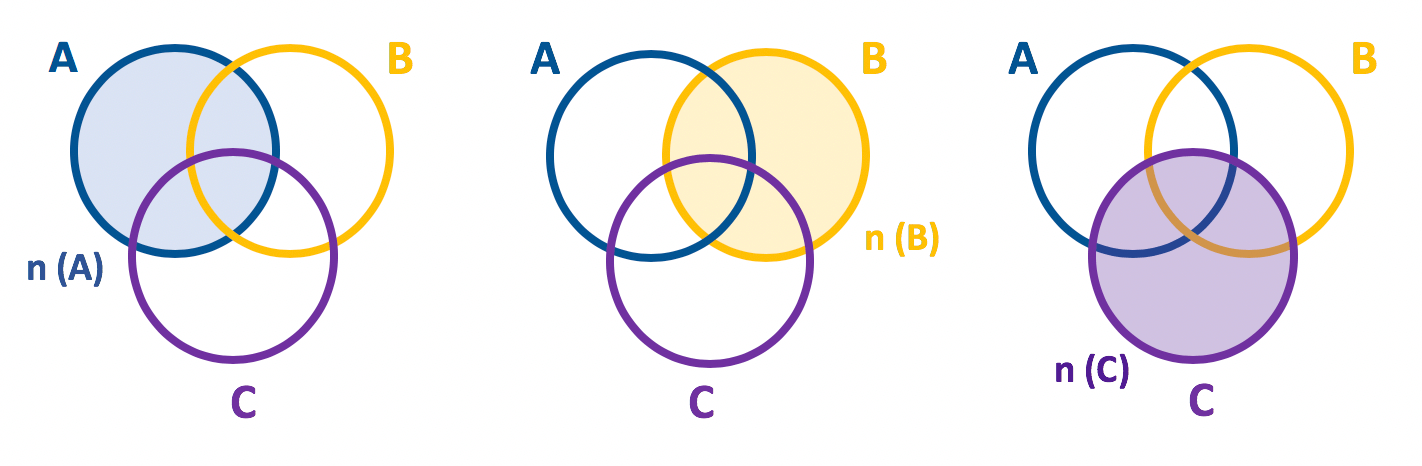
Destacaremos agora, separadamente, as regiões do diagrama em que estão presentes os elementos do conjunto A, B e C. Fiquem atentos ao que irá acontecer!

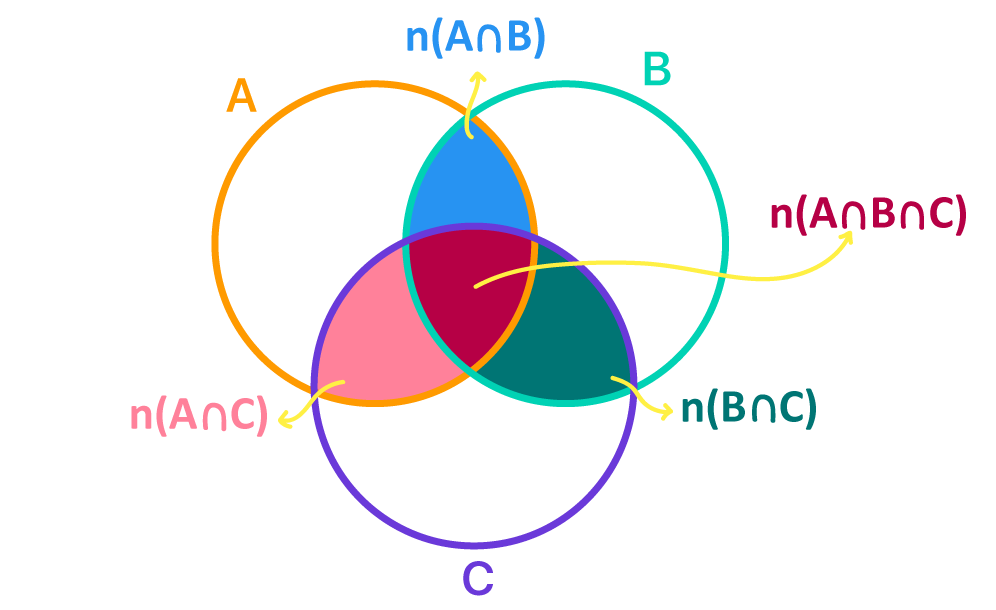
Quem reparou na imagem com atenção, percebeu que existem algumas regiões do diagrama que são comuns, por exemplo, aos elementos de A e B, A e C, B e C, e também de A, B, e C. Essas são as regiões de intersecção entre os conjuntos.

Assim, se partirmos da ideia da fórmula do número de elementos da união entre dois conjuntos, em que primeiro se soma os elementos de todos os conjuntos, e depois subtrai-se o número de elementos repetidos, ou seja, o número de elementos presentes nas regiões de intersecção entre dois conjuntos, temos a seguinte fórmula:

n (A ∪ B ∪ C) = n (A) + n (B) + n (C) – n (A ∩ B) – n (A ∩ C) – n (B ∩ C) + n (A ∩ B ∩ C)

Incrível, não é? E pra quem achou essa fórmula muito difícil de memorizar, aí vai uma dica! Representem os conjuntos citados nas questões do ENEM e dos vestibulares que fizerem em forma de diagrama. Isso com certeza ajudará vocês a lembrarem de todas essas fórmulas que conhecemos hoje.

 

Encerrando o texto com mais algumas dicas!

Agora, convido vocês a dar uma olhada no vídeo que deixo em anexo logo abaixo. Nele, é possível revisar as operações de união e intersecção entre os conjuntos, e de quebra, resolver comigo uma questão prática sobre o número de elementos da união.

Gostou deste conteúdo? Clique aqui para saber como a Plataforma do Professor Ferretto funciona!

Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da Plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!

Um abraço, pessoal! Até mais!