
O conceito de equilíbrio químico está relacionado à capacidade de um sistema químico de manter as concentrações dos reagentes e...
É possível construir os gráficos de funções que possuem a variável no expoente, utilizando os conceitos do gráfico da função exponencial em si. Querem saber como? Então cliquem aqui!
Olá pessoal! Tudo bem com vocês?
Estamos aqui novamente, para estudar a construção dos gráficos daquela famosa função matemática cuja variável se encontra no expoente: a função exponencial! É fato que na parte 1 deste texto, foram obtidos alguns gráficos de funções exponenciais cuja forma era simplesmente f(x) = a x. Em casos como esse, vocês viram, construir um gráfico é quase uma receita de bolo. Só que infelizmente, nem tudo na vida são flores, não é mesmo? Por isso, no texto de hoje, nós vamos aprender como utilizar todos os conceitos vistos na parte 1, para construir gráficos de funções cuja forma aparenta ser um pouco mais complexa!
Trazer uma solução simples, para algo que parece complicado, é justamente o segredo do sucesso para quem pretende fazer as provas do ENEM e dos vestibulares! Que tal contar então, com as dicas e os conhecimentos de um professor, que pode lhes ajudar a tornar mais simples todos os conteúdos da matemática do ensino médio? Esse é o Professor Ferretto! Na sua plataforma de ensino 100% online, vocês encontram videoaulas, exercícios do ENEM e de vestibulares resolvidos em vídeo, plano de estudos, simulados e contam inclusive com a ajuda de monitores treinados no plano diamante. Gostaram da ideia? Então acessem o site e saibam mais!
Bom, antes de iniciarmos os estudos, aqui vai uma dica bem importante: caso vocês não tenham acompanhado o texto Gráfico da Função Exponencial – Parte 1, deem uma olhadinha nele antes de continuar a leitura por aqui! Isso proporcionará a vocês um aprendizado completo sobre o assunto, eu garanto!
Preparados agora? Então vamos lá! Vocês devem ter visto na parte 1 deste texto a seguinte definição:
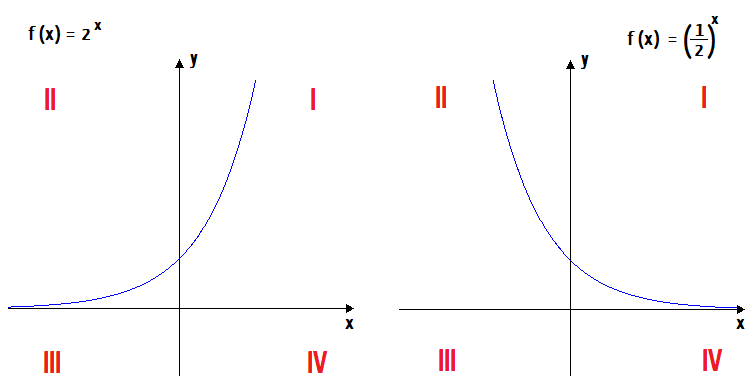
O gráfico de uma função exponencial f(x) = a x, com 0 < a ≠ 1, é chamado de curva exponencial.
Isso significa que uma função exponencial em si, sempre será dada na forma f(x) = ax, sendo que o valor numérico da sua base a, deve ser necessariamente maior que zero, ou positivo, e também diferente de 1 (0 < a ≠ 1). Até aí, nenhuma novidade, não é mesmo? Pois bem, conhecer esse conceito, nos permitiu construir o gráfico de duas funções exponenciais muito interessantes, cuja lei de formação e as respectivas curvas exponenciais vocês podem ver abaixo:
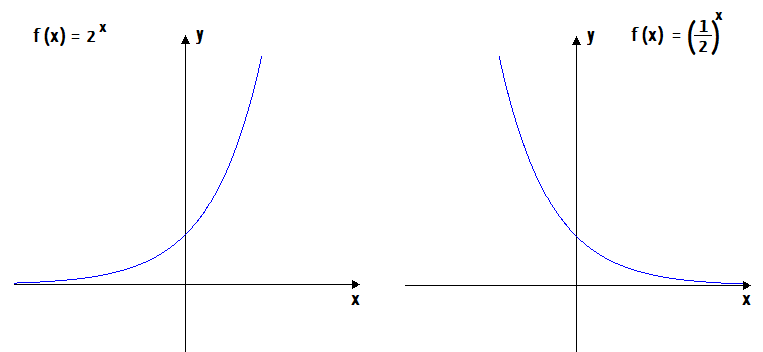
Essas duas curvas nos possibilitaram tirar uma série de conclusões a respeito da representação gráfica de uma função exponencial. Dentre elas, as citadas a seguir são extremamente importantes para o nosso estudo de hoje. Observem-nas com atenção:
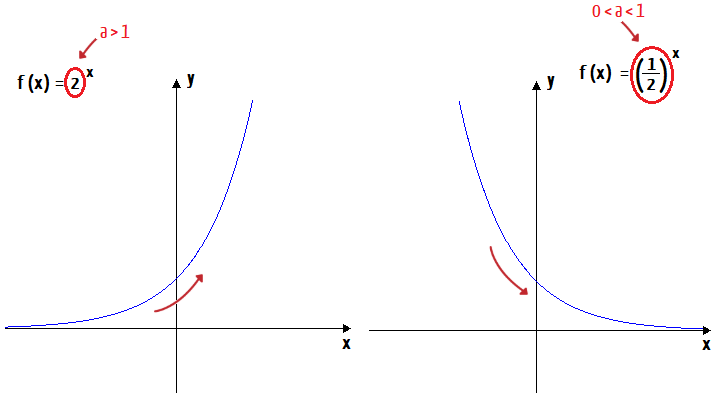
Quando o valor numérico da base a de uma função exponencial é maior que a unidade (a > 1), diz-se que essa função é crescente. Já quando o valor numérico desta mesma base a se situar entre zero e a unidade (0 < a < 1), significa que a função exponencial é decrescente.
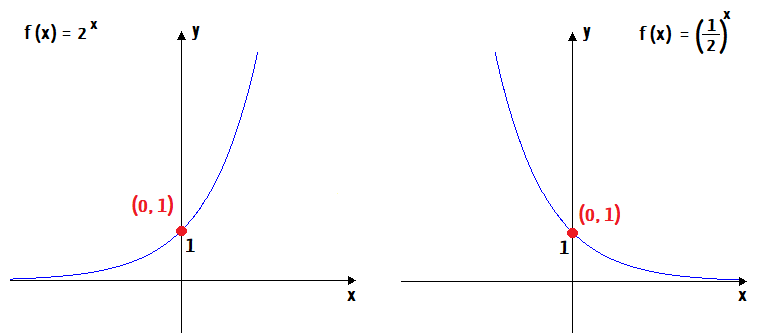
Mas o fato é que independentemente do valor que a base a da função exponencial f(x) = ax assumir, outras duas coisas são certas: a primeira delas, é que o gráfico desta função sempre intersectará o eixo y no ponto (0,1). A segunda, é que esse mesmo gráfico sempre irá se localizar apenas no primeiro e no segundo quadrante do plano cartesiano, ou seja, acima do eixo x, e jamais poderá encostar neste eixo.
Tudo entendido até aqui? Então, baseando-se nessas informações, como vocês construiriam o gráfico das funções apresentadas a seguir?
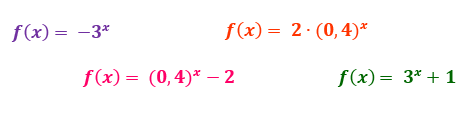
Pessoal, nós não teríamos revisado todas essas características dos gráficos das funções exponencias na forma f(x) = ax, se não fossemos utilizá-las, certo? Por isso, a ideia é que vocês façam da parte das funções que representam uma função exponencial pura, uma nova função g(x), e construam seu gráfico normalmente. Feito isso, vocês tomarão medidas para interpretar o que um valor que multiplica, soma, ou subtrai essa função exponencial causa na sua representação gráfica, e então, estarão prontos para traçar o gráfico da função f(x) como um todo.
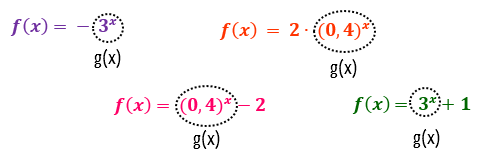
Querem ver como isso funciona? Então continuem comigo aqui!
1. f(x) = – 3x
É verdade que a função f(x) possui uma variável no expoente, mas como um todo, ela não representa uma função exponencial f(x) = ax, devido aquele sinal negativo junto a base da função. Por isso, vamos fazer da parte puramente exponencial de f(x) uma nova função g(x), e construir o seu gráfico normalmente.
g(x) = 3x
Observando a função g(x), nós podemos concluir que:
Essas características nos permitem esboçar o gráfico de g(x) facilmente:
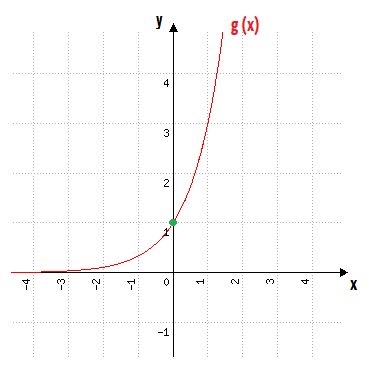
Bom, se g(x) = 3x, então f(x) = – g(x), não é mesmo? Mas o que um sinal negativo na frente de uma função, implica em sua forma gráfica?
Graficamente, quando uma função é multiplicada por -1, significa que a sua forma gráfica sofrerá uma reflexão em relação ao eixo horizontal, ou seja em relação ao eixo x.
Assim, é como se o eixo x funcionasse como um espelho para g(x), de forma que fazendo o espelhamento desta função, temos o gráfico da função original f(x).
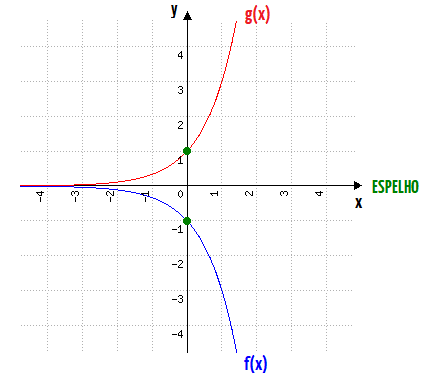
Incrível, não é mesmo? Agora, fiquem atentos ao que irá acontecer no próximo caso.
2. f(x) = 3x + 1
Novamente, é possível ver que a função f(x) possui uma variável no expoente, mas como um todo, ela não representa uma função exponencial f(x) = ax. Por isso, vamos fazer da parte que é puramente exponencial uma nova função g(x), e construir o seu gráfico normalmente. Já que g(x) é exatamente igual a g(x) do exemplo anterior, teremos menos trabalho para esboçar o seu gráfico agora. O único segredo para nós ainda é: o que será que a soma de uma unidade a uma função implica em sua forma gráfica?
g(x) = 3x

Bom, se g(x) = 3x, então f(x) = g(x) + 1, não é mesmo? Olhem só o que isso significa.
Graficamente, quando acrescentamos uma unidade a uma função, significa que a sua forma gráfica sofrerá uma translação vertical positiva, ou seja, ela se deslocará uma unidade para cima, em direção ao sentido positivo do eixo y.
Em outras palavras, todos os valores de y da função g(x), serão acrescidos de uma unidade para formar os valores de y de f(x).
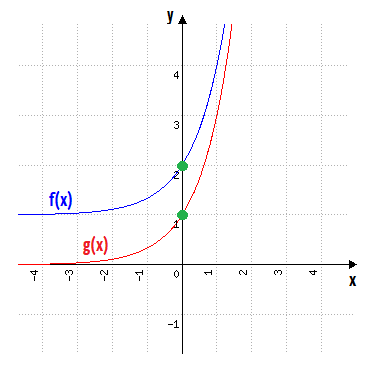
Viram que interessante? Então vamos ver se vocês se ligaram em outro detalhe muito importante. g(x) era uma função puramente exponencial, e por isso, jamais poderia tocar no eixo x. Mas como f(x) é igual a g(x) acrescida de uma unidade, ela jamais poderá tocar a reta horizontal y=1, que se encontra exatamente uma unidade acima do eixo x!
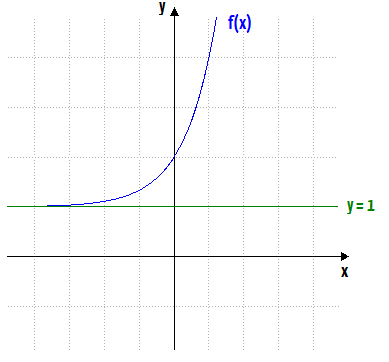
3. f(x) = (0,4)x – 2
f(x) = (0,4)x – 2 não é uma função exponencial em si, não é mesmo? Mas uma parte dela, (0,4)x, está na forma f(x) = ax. Por isso, vamos fazer desta parte uma nova função g(x), e construir o seu gráfico normalmente.
g(x) = (0,4)x
Observando a função g(x), nós podemos concluir que:
Essas características nos permitem esboçar o gráfico de g(x) facilmente:
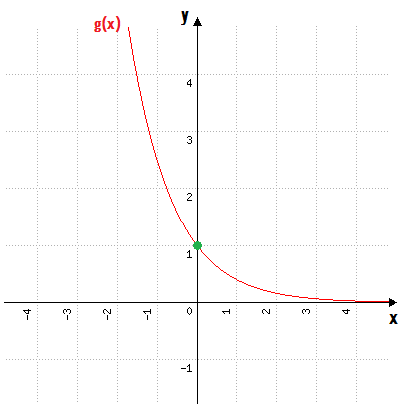
Agora, é claro que se a função g(x) = (0,4)x, então f(x) = g(x) – 2. Alguém adivinha o que isso significa?
Graficamente, quando subtraímos duas unidades de uma função, significa que a sua forma gráfica sofrerá uma translação vertical negativa, ou seja, ela se deslocará duas unidades para baixo, em direção ao sentido negativo do eixo y.
Em outras palavras, serão subtraídas duas unidades de todos os valores de y da função g(x), para formar os valores de y de f(x).
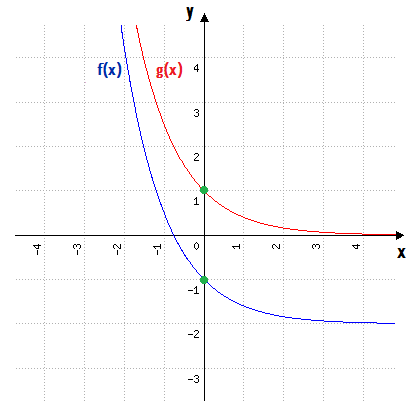
A translação negativa de duas unidades da função g(x), fez com que a forma gráfica da função f(x) ultrapassasse o eixo x, atingindo também os quadrantes 3 e 4 do plano cartesiano. Por isso, devemos ter ciência de que f(x) jamais poderá tocar a reta horizontal y = – 2, que se encontra justamente a duas unidades do eixo das abscissas!
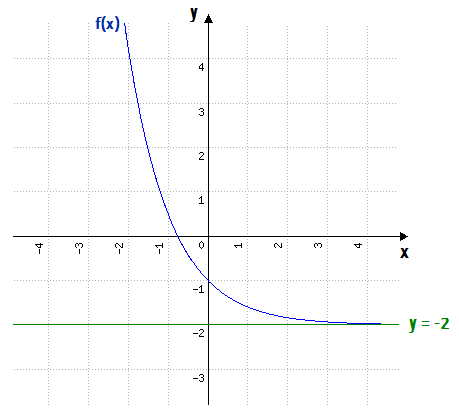
4. f(x) = 2 ∙ (0,4)x
Neste último exemplo, é claro que nós não podíamos perder a oportunidade de utilizar a mesma função g(x) do exemplo anterior, para mostrar o que acontece quando uma função exponencial é multiplicada por 2.
g(x) = (0,4)x
f(x) = 2 ∙ g(x)

Graficamente, quando uma função exponencial é multiplicada por dois, não há qualquer translação ou reflexão em sua forma gráfica, mas sim uma simples duplicação.
Em outras palavras, todos os valores de y da função g(x) serão duplicados para gerar os valores de y de f(x).
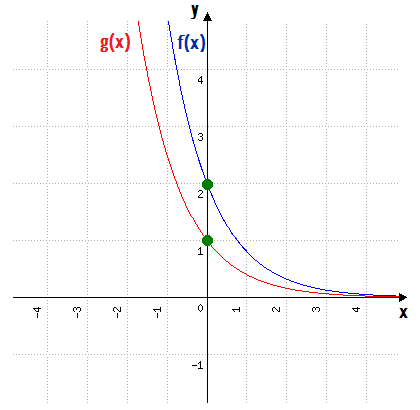
Ficou claro pessoal!? A ideia aqui era mostrar para vocês, como aplicar os conhecimentos necessários a construção dos gráficos da função exponencial f(x) = ax, a qualquer função que possua sua variável no expoente! Mas é claro que existem diversos outros casos de funções como essas, e a melhor forma de entender todos eles é construir uma série de gráficos e treinar bastante. É verdade também, que vocês poderiam ignorar tudo isso e partir logo de cara para as famosas tabelinhas, ou mesmo utilizar uma tabelinha para lhes auxiliar na aplicação dos conceitos que vimos aqui. A minha dica é a seguinte: usem a solução que seja mais rápida e fácil para vocês!
Esse parágrafo soou como uma conclusão, não é mesmo? Pois é, o texto está terminando! Mas não fiquem tristes, afinal estou deixando em anexo um vídeo muito interessante, que complementa todas as informações vistas por aqui. Além disso, só lá vocês encontram mais alguns exercícios resolvidos, então não deixem de assisti-lo!
Desejo a todos ótimos estudos! Um abração!
