EQUAÇÕES EXPONENCIAIS
03/01/2020
Equações exponenciais são equações em que a incógnita aparece nos expoentes. Uma das maneiras de resolver equações como essas, é transformando-as em uma igualdade de potências de mesma base.
Olá, pessoal! Tudo bem?
Hoje vamos falar sobre mais um assunto da matemática de extrema importância para aqueles que pretendem realizar as provas do ENEM ou de alguns vestibulares. As equações exponenciais são equações cuja incógnita aparece no expoente e cuja base deve ser positiva e diferente de 1. Neste texto, nós vamos aprender a resolver as equações exponenciais pensando no conceito de igualdade entre potências de mesma base. Por isso, já vou adiantando: é essencial que as propriedades da potenciação sejam conhecidas quando desejamos resolver esse tipo de equação.
Certo, pessoal?! Então, sem mais delongas, vamos entender direitinho o método que pode ser utilizado para resolver equações exponenciais. Vem comigo aqui!
1. COMO RESOLVER EQUAÇÕES EXPONENCIAIS?
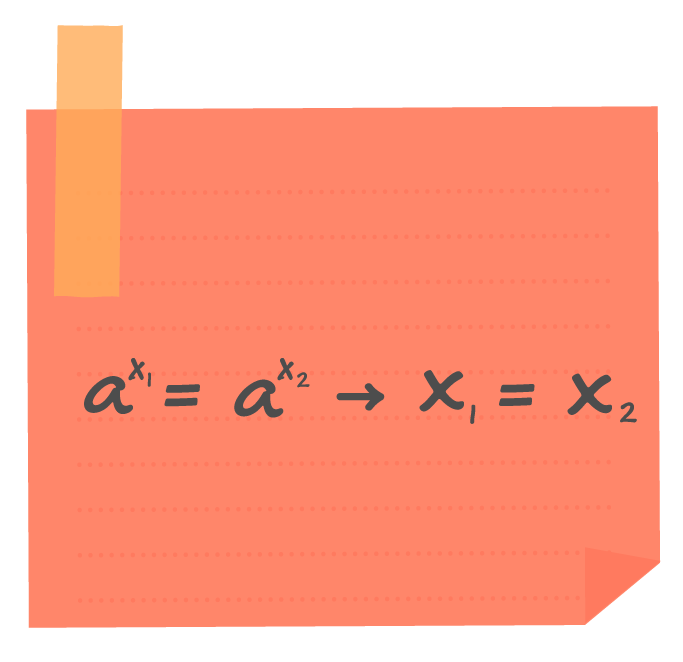
Assim como vimos no início deste texto, é possível resolver boa parte das equações exponenciais transformando-as em uma igualdade de potências de mesma base. Utilizamos essa técnica devido aos motivos apresentados na imagem acima.
![]()
Observem a igualdade com atenção. Se estamos afirmando que uma expressão (ax1) é igual a outra (ax2), é porque o valor numérico equivalente a cada uma delas deve ser igual, como nove é igual a nove (9 = 9), ou como menos cinco é igual a menos cinco (– 5 = – 5), por exemplo. Portanto, se a base a de ambas as expressões é igual, para que o valor numérico resultante de ax1 e ax2 também seja igual, x1 deve ser igual a x2. A partir dessa conclusão é possível “descartar” as bases e trabalhar apenas com uma igualdade entre expoentes (x1 = x2), simplificando a expressão como um todo. Mas sem uma base igual, jamais poderíamos afirmar que os expoentes das expressões seriam equivalentes.
É claro que a título de exemplo, utilizamos como expoentes das expressões exponenciais apenas x1 e x2. Mas não se assustem se durante a resolução de equações exponenciais vocês se depararem com expressões de 1º e 2º grau, expressões com radicais, fracionárias, e tudo que a matemática pode oferecer. Tudo isso tem jeito, pessoal! Agora, o grande problema é quando a base de uma equação exponencial é negativa ou igual a 0 e 1. De acordo com a definição das funções exponenciais, são permitidas apenas bases maiores do que zero e diferentes de 1.
Ficou curioso?

Quer saber por que a base da função exponencial não pode ser 0 e nem 1? Então clique aqui antes de continuar.
Entendido, pessoal? Antes de resolvermos alguns exemplos a fim de entendermos como obter uma igualdade de potências de mesma base, vamos conhecer algumas propriedades que vão nos ajudar muito nesse processo. Vem comigo!
2. AS PROPRIEDADES DA POTENCIAÇÃO

E aí, pessoal, o que acharam deste quadro? Nele vocês encontram as principais propriedades operatórias da potenciação. Vamos utilizar muito a maioria delas para resolver uma série de equações exponenciais nos exemplos seguintes. Sigam comigo!
3. EQUAÇÕES EXPONENCIAIS RESOLVIDAS

Exemplo 1
![]()
Ao observarmos equações como essa, nosso objetivo sempre será igualar as bases das potências. Reparem que nesta equação, temos uma base de valor 3 e outra de valor 81. Não conseguimos reduzir o 3 a base 81, porque 3 é menor que 81, mas podemos reduzir o 81 a base 3. Na dúvida, realizem a fatoração da base maior, e verifiquem se é possível reescrevê-la em função da base menor.
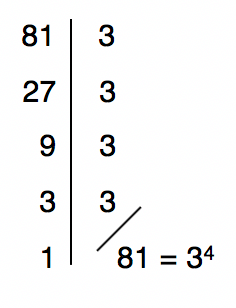
E não é que deu certo? Agora é hora de voltar a nossa equação exponencial inicial deixando o lado esquerdo como está, e substituindo o 81 por 34. Dessa forma, é possível igualar as bases das duas potências, eliminá-las, e trabalhar apenas com os expoentes. Acompanhem comigo!
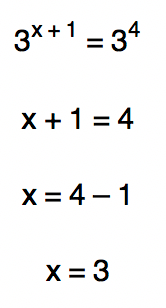
Tranquilo, não é, pessoal? Nossa primeira equação exponencial foi resolvida com sucesso! Em forma de conjunto solução podemos dizer que:
S = {3}.
Exemplo 2
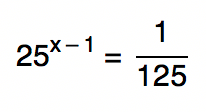
Vamos iniciar a resolução deste exemplo com mais uma super dica. Ao se deparar com uma equação exponencial, verifiquem se os valores numéricos da equação não são potências de um número comum. Se repararmos, por exemplo, nos números 25 e 125, veremos que ambos são potências de 5. Isso significa que podemos reduzi-los a base 5, já que 25 = 5², e 125 = 5³. Substituindo esses valores na expressão, ficamos com:
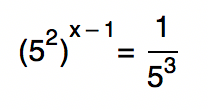
Percebam que a partir deste momento torna-se necessário o uso das propriedades da potenciação para dar sequência a resolução. No lado esquerdo da igualdade, nós podemos aplicar a propriedade 3 (P3), afinal temos uma potência de potência. Já no lado direito da igualdade, podemos aplicar a propriedade 6 (P6), e passar o 5³ para o numerador. Olhem só como fica:
![]()
Finalmente encontramos uma igualdade de potências de mesma base! Resta-nos então, igualar os expoentes e trabalhar apenas com eles. Fiquem de olho!
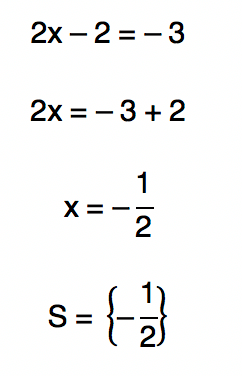
Beleza, pessoal? Bom, até agora nós resolvemos algumas equações exponenciais consideradas bastante simples. Nos próximos exemplos, vamos resolver equações que exigem a utilização de mais artifícios matemáticos para serem solucionadas. Vocês não vão perder esses exemplos, não é? Sigam comigo!
Exemplo 3
![]()
A equação deste exemplo seria semelhante àquelas que acabamos de resolver, não fosse um pequeno detalhe: o número 3 que está multiplicando o termo exponencial a esquerda da igualdade. Sem problemas, afinal, quem está multiplicando pode passar para o outro lado da igualdade dividindo, não é mesmo?
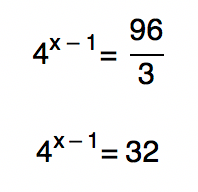
Vejam que a partir desse momento, nós já sabemos como resolver o caso. Se fatorarmos o número 32, como fizemos lá no primeiro exemplo deste texto, acabaremos descobrindo que 32 = 25. Além disso, também podemos dizer que 4 = 2², não é? Assim, substituindo esses dois valores na nossa equação, e aplicando mais uma vez a propriedade da potenciação número 3, chegamos ao tão esperado conjunto solução da equação.
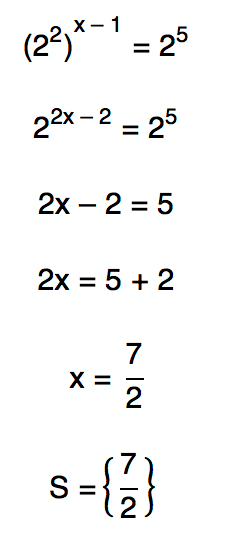
A matemática pode ser mesmo fascinante, não é? Vamos então ao nosso último exemplo, em que apresento a vocês outros artifícios matemáticos muito interessantes. Vem comigo!
Exemplo 4
![]()
Reparem que nesta equação existe uma soma de termos exponenciais em um dos lados da igualdade. Ambos possuem a mesma base, e expoentes com operações de soma (x + 2) e subtração (x – 1). Utilizando as propriedades 1 e 2 dadas no quadro das propriedades da potenciação, podemos reescrever essas potências da seguinte forma:
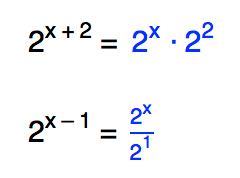
Voltando a equação inicial, temos que:
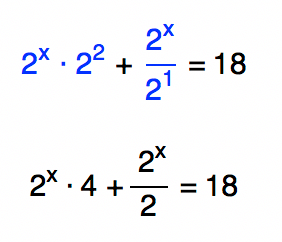
Neste momento, reparem que o termo exponencial 2x se encontra em duas parcelas da equação. Para resolver esse impasse, vamos coloca-lo em evidência, e depois de algumas operações básicas chegaremos ao conjunto solução desejado.
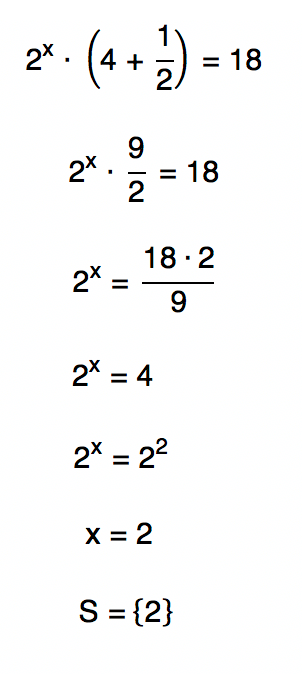
E aí, pessoal, o que acharam deste texto? Espero que todos os conceitos e exemplos vistos por aqui tenham sido bem proveitosos para os estudos de vocês! E quem quiser resolver mais algumas equações exponenciais pode ficar à vontade para ver os vídeos que estou deixando em anexo. Lá vocês encontram alguns exemplos mais complexos, que complementam a preparação para as provas do ENEM e dos vestibulares!
E pra finalizar, aí vai outro convite irrecusável: que tal conhecer a plataforma do Professor Ferretto? Clique aqui para saber como ela funciona!
Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!
Um abração e bons estudos, pessoal! Até breve!