
Os assuntos de biologia que mais caem no Enem s√£o uma das preocupa√ß√Ķes de quem est√° se preparando para a...
Voc√™ sabe como calcular o n√ļmero de elementos da uni√£o entre 2 e 3 conjuntos? E se os conjuntos forem disjuntos? Acesse o texto e descubra todas as f√≥rmulas que envolvem o assunto!
Existe uma f√≥rmula capaz de definir facilmente o n√ļmero de elementos da uni√£o entre dois conjuntos A e B. Baseando-se nela, √© poss√≠vel obter uma segunda f√≥rmula: a do n√ļmero de elementos da uni√£o entre tr√™s conjuntos, A, B e C.
 
Olá, pessoal! Como vão vocês?
Estamos bastante acostumados a encontrar o conjunto uni√£o entre dois conjuntos A e B. Contudo, dificilmente nos preocupamos com o n√ļmero, ou com a quantidade de elementos desse conjunto. N√£o parece, mas a verdade √© que essa informa√ß√£o pode nos ajudar a resolver diversas quest√Ķes do ENEM, e principalmente de vestibulares.
Por isso, aprenderemos no texto de hoje a f√≥rmula do n√ļmero de elementos da uni√£o entre 2 e 3 conjuntos. Faremos tamb√©m alguns exemplos, para consolidar todo esse conhecimento. Quem est√° pensando em prestar vestibulares logo mais, ter√° de seguir comigo!
Beleza, pessoal? Então, é hora de iniciarmos os estudos. Vem comigo!
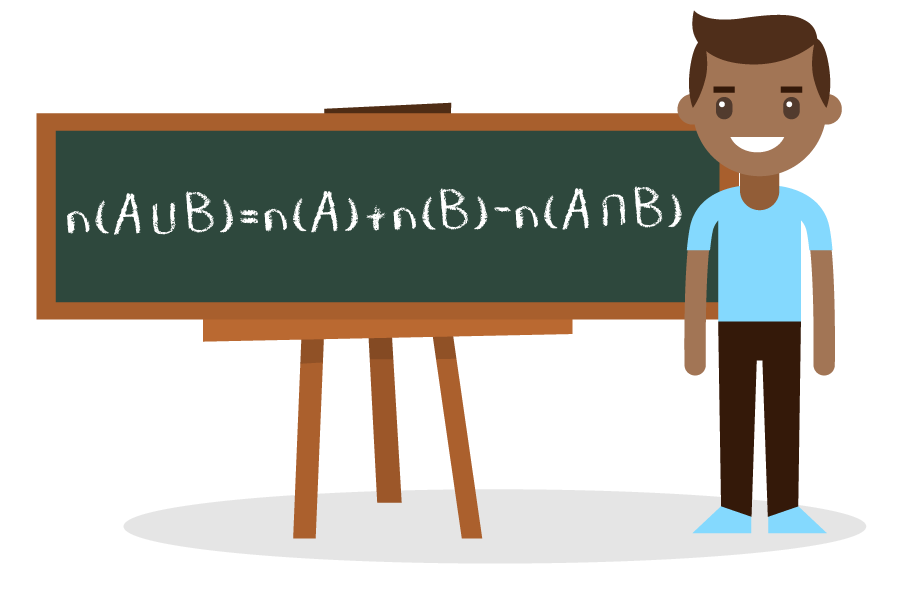
Então, o que acharam da fórmula apresentada na imagem acima? Eu sei, parece confuso determinar a quantidade de elementos do conjunto união entre os conjuntos A e B. Mas tenho certeza de que partindo de um exemplo, tudo ficará mais claro. Deem uma olhada nos conjuntos A e B descritos abaixo.
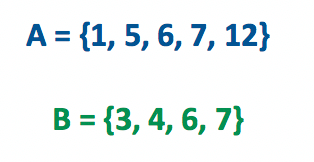
A união entre dois conjuntos A e B pode ser definida como o conjunto formado pelos elementos que pertencem a A ou a B, de acordo com o texto União e Intersecção. Isso significa que a união dos conjuntos A e B apresentados acima, é um conjunto formado pelos elementos que pertencem ou a A, ou a B, ou a ambos os conjuntos.
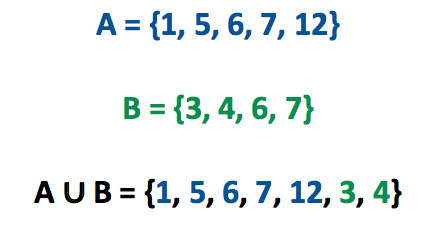
Vejam que para determinar o conjunto união entre A e B, nós copiamos todos os elementos de A, e depois copiamos todos os elementos de B. Mas como haviam dois elementos em comum entre os conjuntos (6 e 7), não houve a necessidade de copiá-los novamente. Quando os conjuntos são representados na forma de diagrama, fica ainda mais fácil determinar união entre eles.
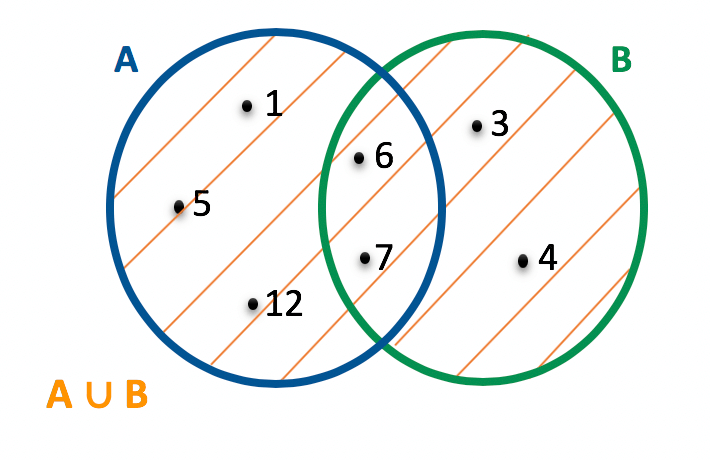
Claro! Neste caso, é só copiar todos os elementos dispostos no diagrama. Isso porque nessa forma de representação, os elementos comuns a ambos os conjuntos já ficam em evidência na região entrelaçada.
Bom, se os elementos que s√£o comuns aos conjuntos A e B fazem diferen√ßa na hora de montarmos o conjunto uni√£o entre eles, √© claro que tamb√©m fazem diferen√ßa¬†na hora de determinar o n√ļmero de elementos deste conjunto, n (A ‚ą™ B).
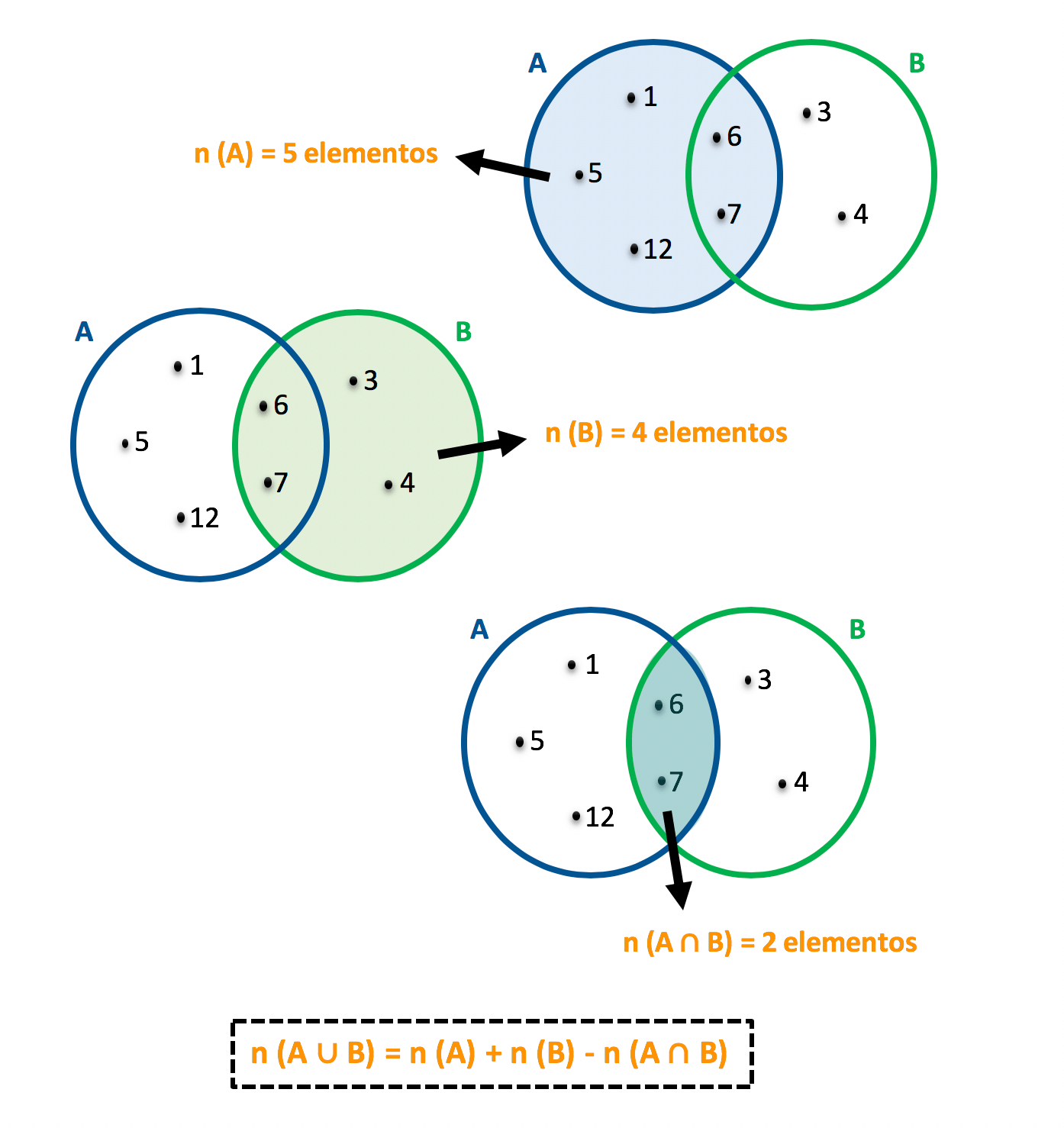
Assim faz todo o sentido, n√£o √© mesmo? Como os termos n(A) e n(B) contabilizam o n√ļmero de elementos comuns a ambos os conjuntos, precisamos descont√°-los uma vez, ou estaremos levando em conta elementos repetidos.

Querem ver como √© verdade? Contando os elementos do conjunto uni√£o que hav√≠amos obtido, A ‚ą™ B = {1, 5, 6, 7, 12, 3, 4}, √© fato que este possui 7 elementos. Vamos usar a f√≥rmula do n√ļmero de elementos da uni√£o para ver se o resultado √© equivalente.

n (A ‚ą™ B) = n (A) + n (B) ‚Äď n (A ‚ą© B)
n (A ‚ą™ B) = 5 + 4 ‚Äď 2
n (A ‚ą™ B) = 7
E não é que deu certo? Aproveitaremos a deixa para desenvolver um novo exemplo!
Dados os conjuntos A = {1, 3, 5 ,7, 9} e B = {2, 3, 5, 7}, determine o n√ļmero de elementos da uni√£o de A e B.
Observando rapidamente os conjuntos dispostos no enunciado, podemos concluir que:
Assim, o n√ļmero de elementos da uni√£o de A e B, √© dado por:
n (A ‚ą™ B) = n (A) + n (B) ‚Äď n (A ‚ą© B)
n (A ‚ą™ B) = 5 + 4 ‚Äď 3
n (A ‚ą™ B) = 6
Para provar que o resultado est√° correto, vamos encontrar o conjunto uni√£o de A e B. √Č poss√≠vel perceber que ele realmente possui 6 elementos:
A¬†‚ą™¬†B = {1, 2, 3, 5, 7, 9}
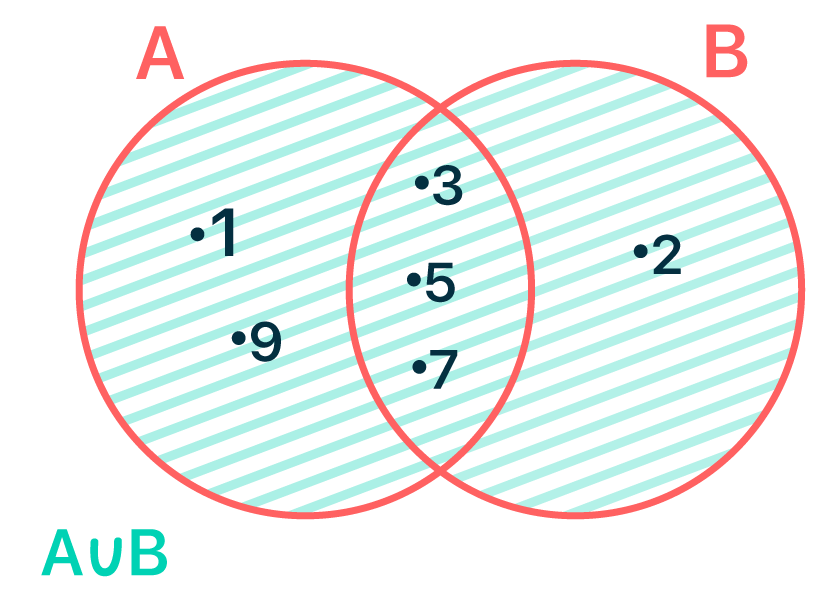
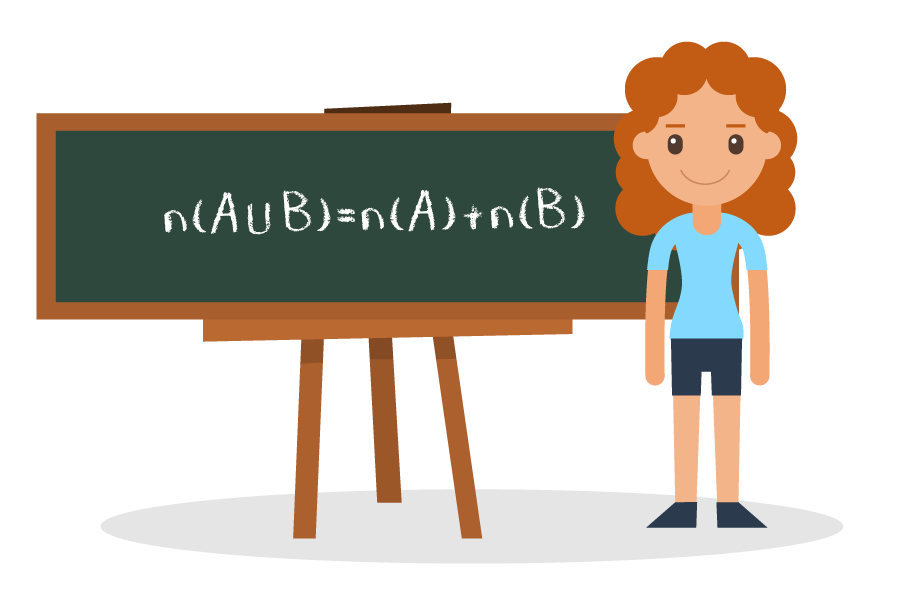
Sendo A e B dois conjuntos disjuntos, ou seja, dois conjuntos que n√£o possuem elementos em comum, √© fato que A ‚ą© B = ‚ąÖ. Assim, o termo n (A ‚ą© B) da f√≥rmula do n√ļmero de elementos da uni√£o se torna nulo, ou igual a zero. Isso possibilita resumir a express√£o que acabamos de conhecer.
Quando dois conjuntos A e B s√£o disjuntos, o c√°lculo do n√ļmero de elementos da uni√£o de A e B se resume a express√£o n (A ‚ą™¬†B) = n (A) + n (B).
Tranquilo, n√£o √© mesmo? Agora, para findarmos este texto com chave de ouro, vamos partir da mesma ideia aplicada ao n√ļmero de elementos da uni√£o de dois conjuntos para deduzirmos a f√≥rmula do n√ļmero de elementos da uni√£o entre tr√™s conjuntos. A representa√ß√£o em forma de diagrama vai nos ajudar novamente. Vem comigo!
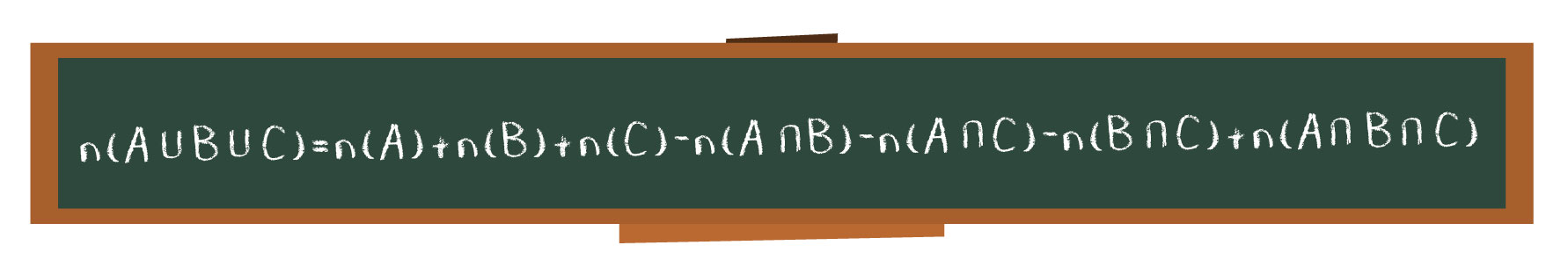
E aí, o que acharam do tamanho desta fórmula? Vamos começar nossa dedução partindo da representação em forma de diagrama de 3 conjuntos A, B e C. Pensaremos aqui em conjuntos que possuem apenas alguns elementos em comum, e por isso, seus diagramas poderão se entrelaçar.
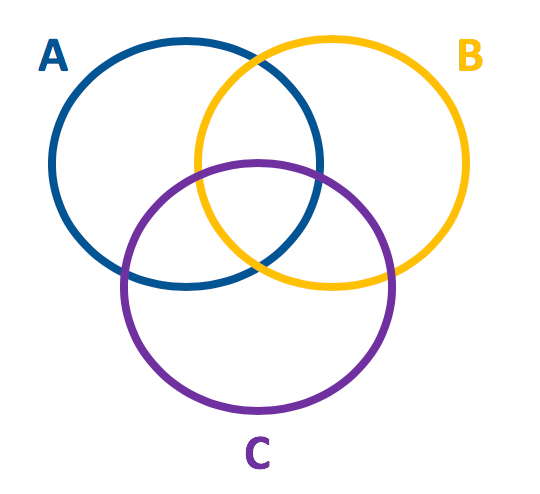
Destacaremos agora, separadamente, as regi√Ķes do diagrama em que est√£o presentes os elementos do conjunto A, B e C. Fiquem atentos ao que ir√° acontecer!
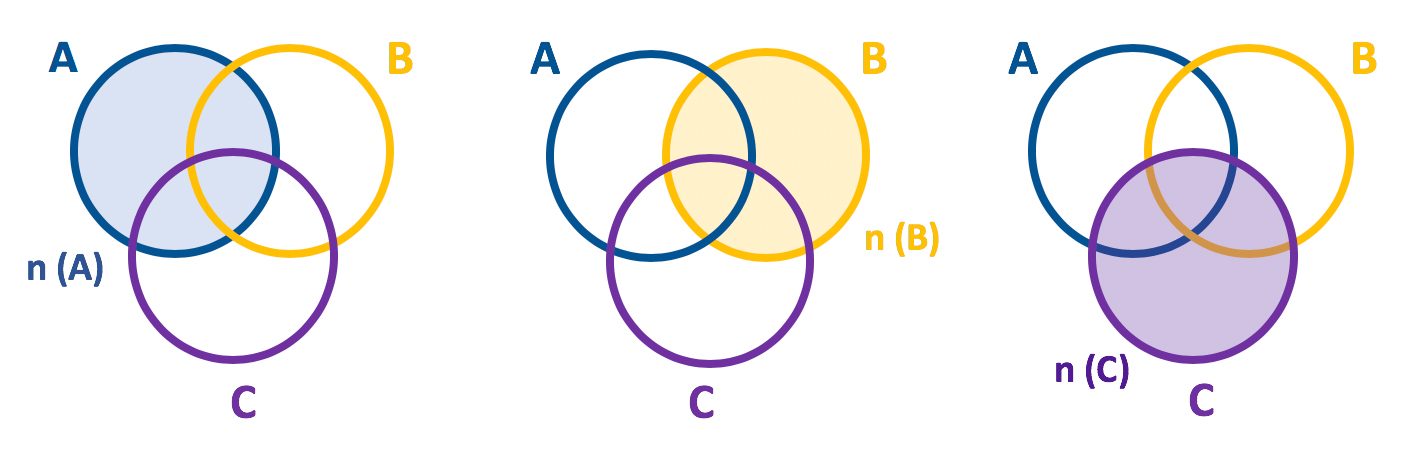
Quem reparou na imagem com aten√ß√£o, percebeu que existem algumas regi√Ķes do diagrama que s√£o comuns, por exemplo, aos elementos de A e B, A e C, B e C, e tamb√©m de A, B, e C. Essas s√£o as regi√Ķes de intersec√ß√£o entre os conjuntos.
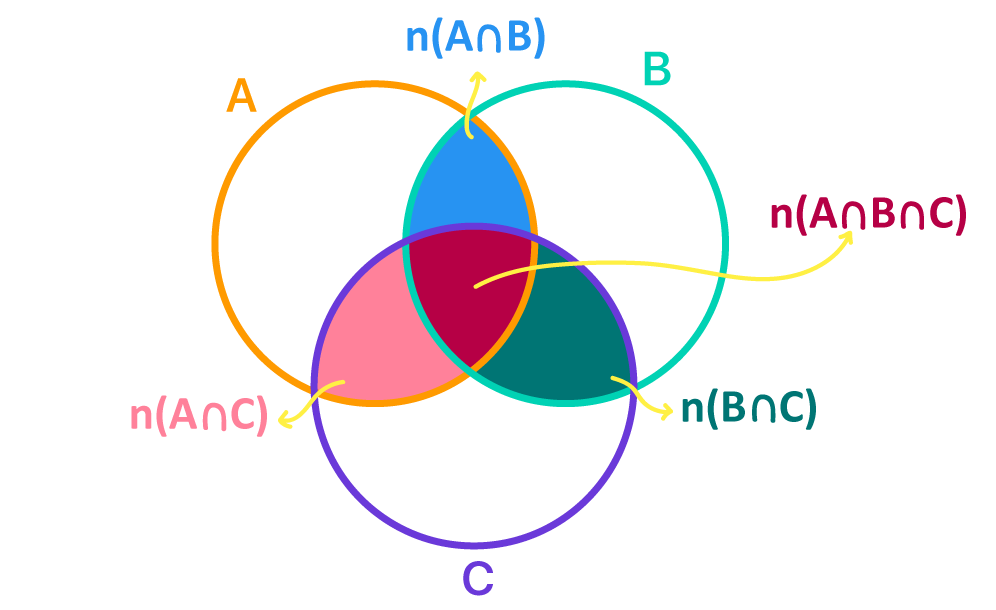
Assim, se partirmos da ideia da f√≥rmula do n√ļmero de elementos da uni√£o entre dois conjuntos, em que primeiro se soma os elementos de todos os conjuntos, e depois subtrai-se o n√ļmero de elementos repetidos, ou seja, o n√ļmero de elementos presentes nas regi√Ķes de intersec√ß√£o entre dois conjuntos, temos a seguinte f√≥rmula:
n (A ‚ą™ B ‚ą™ C) = n (A) + n (B) + n (C) ‚Äď n (A ‚ą© B) ‚Äď n (A ‚ą© C) ‚Äď n (B ‚ą© C) + n (A ‚ą© B ‚ą© C)
Incr√≠vel, n√£o √©? E pra quem achou essa f√≥rmula muito dif√≠cil de memorizar, a√≠ vai uma dica! Representem os conjuntos citados nas quest√Ķes do ENEM e dos vestibulares que fizerem em forma de diagrama. Isso com certeza ajudar√° voc√™s a lembrarem de todas essas f√≥rmulas que conhecemos hoje.
Agora, convido voc√™s a dar uma olhada no v√≠deo que deixo em anexo logo abaixo. Nele, √© poss√≠vel revisar as opera√ß√Ķes de uni√£o e intersec√ß√£o entre os conjuntos, e de quebra, resolver comigo uma quest√£o pr√°tica sobre o n√ļmero de elementos da uni√£o.
Gostou deste conte√ļdo?¬†Clique aqui¬†para saber como a¬†Plataforma do Professor Ferretto¬†funciona!
Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da Plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!
Um abraço, pessoal! Até mais!
