INEQUAÇÕES EXPONENCIAIS – PARTE 2

Olá, pessoal! Tudo tranquilo?

Na parte 1 deste texto, vocês ficaram sabendo que as inequações exponenciais são todas aquelas inequações cuja incógnita encontra-se no expoente. Na maioria das vezes, vocês viram, ao resolver inequações como essas, nós acabávamos caindo em situações semelhantes as inequações do primeiro grau, que felizmente são bastante simples. Contudo, a verdade é que a solução de algumas inequações exponenciais também pode terminar em inequações do 2º grau, o que acreditem, pode dar um pouquinho mais de trabalho!

Outra situação muito comum, é que sejam apresentadas inequações exponenciais com dois sinais de desigualdade, as famosas inequações exponenciais simultâneas! E como esses dois casos são muito importantes para o aprendizado de todos os estudantes do ensino médio, nós vamos dar ênfase a eles neste texto! Mas para que tudo fique bem entendido, eu preciso da ajuda de vocês: antes de iniciar essa leitura, deem uma revisada nas inequações do 2º grau, no estudo do sinal de uma função quadrática, na operação de intersecção entre dois conjuntos, e também nas inequações simultâneas do 1º e do 2º grau. Pronto, com toda essa bagagem, não haverá prova de vestibular que os detenha!

Pessoal, é claro que eu sei que é difícil conhecer bem todo esse conteúdo da matemática do ensino médio a tempo de realizar as provas do ENEM e dos vestibulares. Mas se vocês tiverem acesso a plataforma de estudos 100% online do Professor Ferretto, certamente ficará muito mais fácil! Lá tem todo o conhecimento que vocês precisam em aulas didáticas, e com foco na interpretação das questões! Além disso, são disponibilizados simulados semanais, mais de 1000 questões do ENEM e dos vestibulares resolvidas em vídeo, e até aulas de física para todos os assinantes! Sejam vocês também alunos do Professor Ferretto! É simples, basta acessar o site!

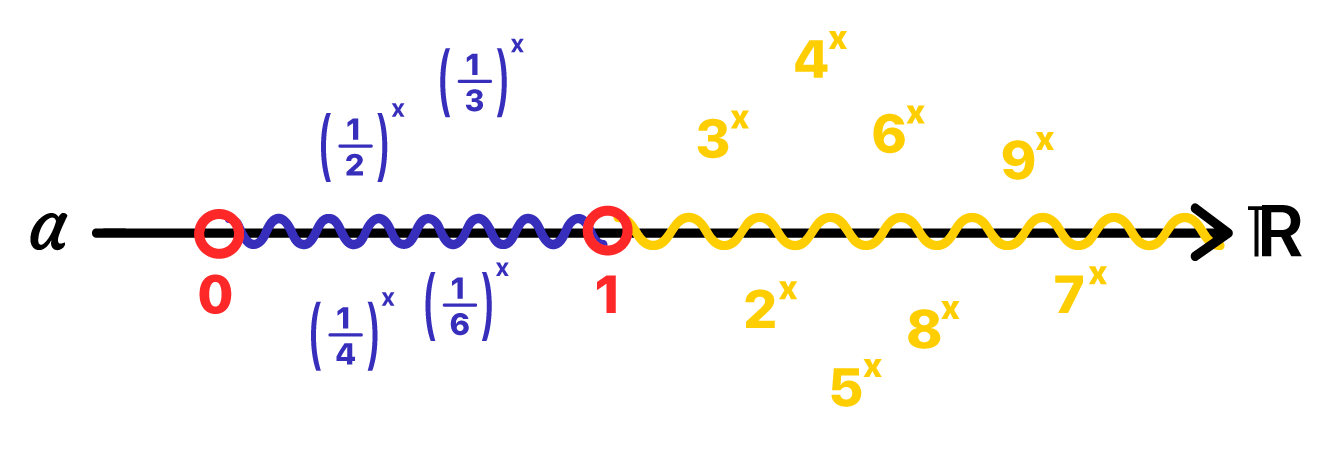
E agora, chega de papo, afinal, temos muito o que aprender hoje! Apesar de tratarmos de casos de inequações exponenciais diferentes dos que foram apresentados na parte 1, uma coisa é certa: valor numérico da base a continua sendo determinante para resolução destas inequações.

Se a base for maior que 1, mantenha o sinal de desigualdade, mas se a base for um valor entre 0 e 1, inverta o sinal de desigualdade!

Ao nos depararmos com uma inequação exponencial, tudo que temos que fazer é dar um jeito de obter uma desigualdade de potências de mesma base. Depois que as bases são iguais, é possível cancelá-las, e de acordo com o seu valor numérico, o sinal de desigualdade que havia entre as potências será mantido ou será invertido em relação aos seus expoentes.

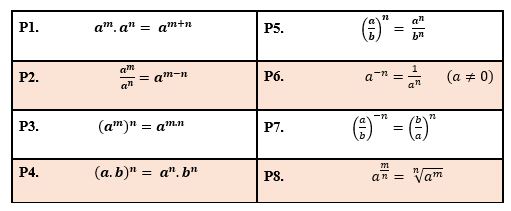
Lembraram de tudo isso? Também é imprescindível termos fresquinho na mente as conhecidas propriedades da potenciação, seja para a resolução de inequações, ou mesmo para solucionar as próprias equações exponenciais. Pois é, pessoal, até tentei fugir da nossa conhecida tabelinha das propriedades, mas não vai ter jeito: lá vem ela novamente!

Pois bem, agora que os aspectos mais importantes das inequações exponenciais foram revisados, vamos ao que foi prometido! Acompanhem comigo o nosso primeiro exemplo…

Mas que interessante! Parece que não vamos ter trabalho algum para gerar uma desigualdade de potências de mesma base, afinal, as bases que nos foram entregues já possuem o mesmo valor! A fração ¼, corresponde ao valor decimal 0,25, que se encontra entre 0 e 1. Isso nos permite concluir o seguinte: podemos cancelar as bases das potências, mas precisaremos inverter o sinal de desigualdade que há entre elas em relação aos seus expoentes.

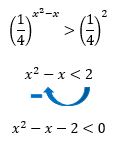
Estava fácil demais, não é mesmo? Como foi dito no início do texto, chegamos ao ponto em que a resolução de uma inequação exponencial passa a depender inteiramente da solução de uma inequação do 2º grau. Mas não se preocupem, isso não chega a ser um grande problema: só precisamos lembrar como resolvíamos essas tais inequações do segundo grau, e pronto!

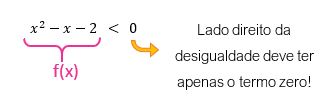
Como não é possível isolar a incógnita x de uma expressão do 2º grau completa, o primeiro passo para resolver uma inequação do 2º grau consiste em transformar o lado esquerdo da desigualdade em uma função. Mas antes disso, deve-se prestar atenção em um detalhe importante: o lado direito da desigualdade deve necessariamente ter apenas o termo zero. Aí fica claro porque nós passamos o número 2 para o lado esquerdo da desigualdade quando cancelamos as bases da nossa inequação exponencial!

Pois bem, o fato é que a solução da inequação x² – x – 2 < 0, irá se basear no estudo do sinal da função quadrática ƒ(x) que acabamos de formar. Isso significa que precisaremos esboçar o gráfico da função ƒ(x) = x²– x – 2, a famosa parábola! Bom, quem deu uma olhada no texto Aplicando o estudo do sinal de uma função do 2º grau, já sabe que não há como esboçarmos qualquer parábola sem o conhecimento da sua concavidade e da natureza das raízes da função. Então o que estamos esperando? Vamos logo obter esses parâmetros!

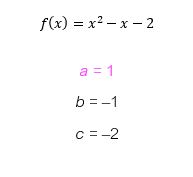
Olhem só que legal! O coeficiente ada função que formamos é um valor positivo, ou maior do que zero. Isso significa que a concavidade da parábola que esboçaremos logo mais será voltada para cima!

∆ = b²– 4·a·c

∆ = (–1)²– 4·1·(–2)

∆ = 1 + 8

∆ = 9

Quando o valor do discriminante, ou delta (∆) de uma função quadrática é positivo, significa que esta função possui duas raízes reais e distintas. Mas para conhecer o valor numérico de cada uma delas, é necessário utilizar a conhecida fórmula de Bhaskara, ou então o método da soma e produto. Por didática, vamos encarar a primeira opção:

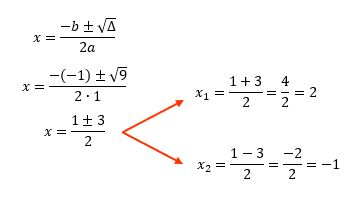
Beleza, pessoal? Parece que chegou a hora de esboçarmos o gráfico da função ƒ(x)! Observem desde já, os valores de x que tornam a função positiva, negativa e também igual a zero. Não parece, mas isso é bem importante, tendo em vista que na sequência, nós voltaremos a dar uma olhada na nossa inequação inicial, e aí teremos certeza de quais desses valores farão parte da solução da questão.

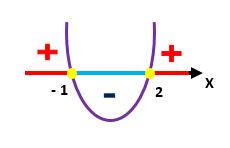
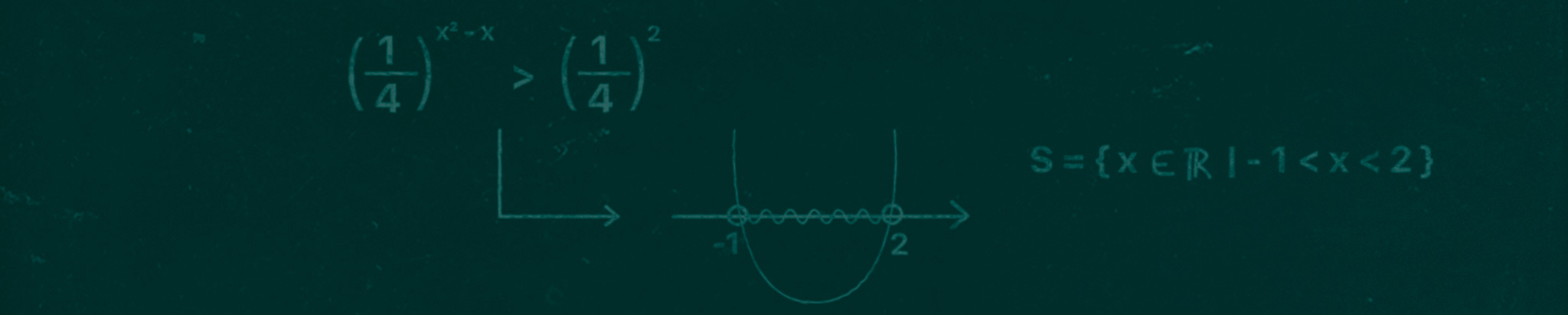
Voltando a inequação inicial, x² – x – 2 < 0, podemos perceber que o sinal de desigualdade <, sugere que devemos obter os valores de x que tornam a função ƒ(x) = x² – x – 2 menor do que zero, ou negativa. Sabendo que uma função é negativa quando o seu gráfico se encontra abaixo do eixo x, e observando o esboço acima atentamente, pode-se perceber que os únicos valores que satisfazem a condição desejada se situam entre –1 e 2, sem incluir os próprios –1 e 2, ou as raízes da função.

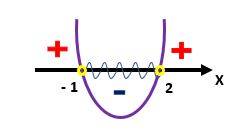
S = {x ∈ ℝ | –1 < x < 2}

E aí, pessoal, o que acharam dessa resolução? Vejam que não teve nada de difícil, apenas uma grande quantidade de passos realizados. Mas não se preocupem: o próximo caso que vamos abordar será muito mais breve. Vem comigo aqui!

E não é que existem mesmo inequações exponenciais que apresentam dois sinais de desigualdade? Pois então, essa é uma das maneiras de se representar uma inequação simultânea!

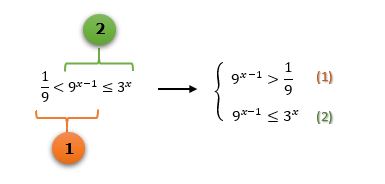
Resolver qualquer tipo de inequação simultânea, significa basicamente encontrar uma solução que satisfaça duas inequações ao mesmo tempo. Por isso, nós separamos a inequação do exemplo em duas, formando um pequeno sistema de inequações. O próximo passo, consiste em resolver cada uma delas separadamente, o que gerará duas soluções diferentes:

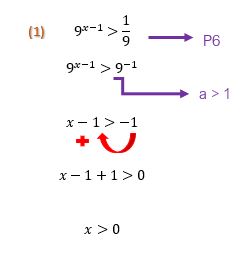
Vejam como é quase impossível escapar das propriedades da potenciação. No primeiro passo da resolução acima, já foi necessário utilizar a propriedade 6, que se encontra naquela tabela lá no início do texto. Outro detalhe que deve ser observado, é o valor das bases das potências de ambos os lados da desigualdade: 9 é maior que 1, por isso, o sinal de desigualdade foi mantido entre os expoentes depois que as bases foram canceladas!

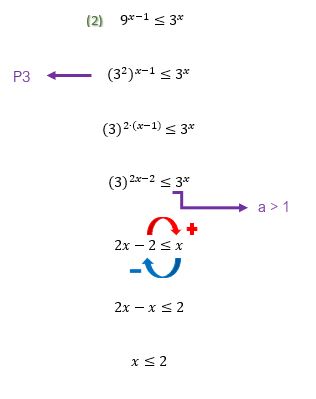
Reparem que a resolução desta segunda inequação também não teve muito mistério. Utilizamos mais uma propriedade da potenciação, a de número 3, e novamente nos deparamos com uma base de valor maior que 1. Melhor que isso, impossível: manteve-se o sinal de desigualdade após o cancelamento das bases das potências.

Até aí tudo certo, não é, pessoal? Pois bem, agora nós temos duas soluções em mãos: para a primeira inequação, qualquer valor de x maior que zero satisfaz a desigualdade, enquanto que para a segunda inequação, só satisfaz a desigualdade qualquer valor de x que seja menor ou igual a 2. Como nosso objetivo não é obter duas soluções diferentes, mas sim uma única solução que satisfaça as duas inequações como um todo, chegou a hora de realizarmos a intersecção entre os dois resultados!

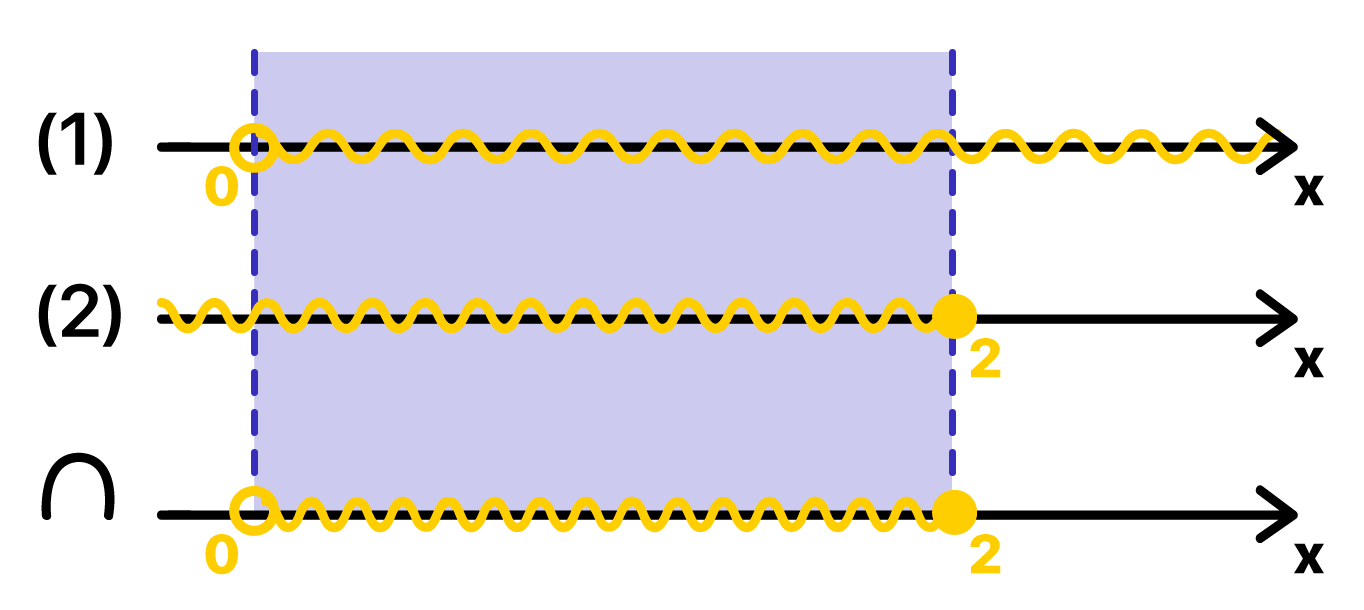
Depois que as soluções são representadas geometricamente, fica muito mais fácil de determinar os valores de x que satisfazem ambas as inequações, vocês não acham? Para valores de x que se situam entre 0 e 2, incluindo o próprio 2 (bolinha fechada), a solução das duas inequações é verdadeira.

S = {x ∈ ℝ | 0 < x ≤ 2}

Estamos chegando ao final deste texto, mas antes de concluirmos, gostaria de tranquilizar aqueles que ficaram na dúvida sobre a operação de intersecção que acabamos de realizar. No vídeo que está em anexo, eu explico direitinho todo esse desenvolvimento, e também mais uma série de detalhes sobre tudo o que foi abordado!

É incrível como alguns conteúdos da matemática que a princípio pareciam distintos, conseguem se entrelaçar! Por isso, vou ficando por aqui, mas não pensem que vou demorar! Logo logo estou de volta para explorarmos mais matemática juntos!

Um abração a todos! Tenham sempre bons estudos!