EQUAÇÕES MODULARES – PARTE 2

Olá pessoal, tudo bem?

Como vocês já sabem, as equações modulares são todas aquelas em que a incógnita aparece dentro de módulos. Na parte 1 deste texto, nós resolvemos uma série de equações modulares que tinham relação com as equações do 1º grau. Por isso, hoje o foco será direcionado totalmente àquelas equações modulares que exigem o conhecimento das equações do 2º grau, e aí, finalmente estaremos preparados para enfrentar qualquer desafio! É claro que conhecer a definição e as propriedades do módulo, permanece sendo essencial para a compreensão de todos os exemplos que serão vistos por aqui!

As equações modulares são muito importantes para todos os estudantes do ensino médio, mas principalmente para aqueles que irão prestar as provas dos vestibulares! Por isso, na plataforma do Professor Ferretto, todo o conteúdo que envolve a função modular está dentro do plano de estudos focado nos vestibulares! Mas quem vai prestar apenas as provas do ENEM não precisa se preocupar: tem um plano de estudos que aborda somente os conteúdos dessa prova também! O curso de matemática do Ferretto é 100% online, e vocês assistem as aulas quando e onde quiserem, sem perder tempo com os conteúdos que não vão utilizar! Acessem o site para conhecer todos os benefícios e as formas de acesso ao curso!

E agora, chega de conversa, porque o primeiro exemplo está chegando! Mas antes, é muito importante que vocês se lembrem bem do conceito apresentado no quadro abaixo, olhem só:

Se módulo de x é igual a um certo valor numérico, que no caso do exemplo é 4, então tanto faz se x assumir o valor 4, ou o valor oposto a ele, que é – 4.  Tanto módulo de 4, quanto módulo de –4 são iguais a 4. É aí que entra a famosa frase que iremos utilizar para determinar a solução de todas as equações que resolveremos hoje: o módulo de qualquer número real, seja ele positivo ou negativo, sempre resultará em um valor positivo!

Entendido? Então, peguem os seus materiais de estudo e venham comigo aqui!

 

1. | x |² – 3| x | – 10 = 0

É possível perceber que essa expressão realmente se assemelha a uma equação do 2º grau, mas como ambas as incógnitas x encontram-se dentro de módulos, tem-se na verdade uma equação modular. Em casos como esse, a melhor solução é optar por uma transformação de variável.

| x | = y

Quando afirmamos que módulo de x é igual a y, ou a qualquer outra variável de preferência, significa que podemos substituir todos os módulos de x da equação por y, e resolvê-la normalmente, como se fosse mesmo uma equação do 2º grau. Só não podemos esquecer de retornar a igualdade acima após obtermos as soluções da equação, afinal, não queremos as soluções para a variável y, mas sim para a variável x.

| x |² – 3| x | – 10 = 0

y ² – 3y – 10 = 0

Ao resolvermos uma equação do 2º grau, nós estamos em busca de suas raízes. E para encontrar essas raízes, nada melhor do que utilizar a fórmula de Bhaskara, não é mesmo? É isso que faremos agora!

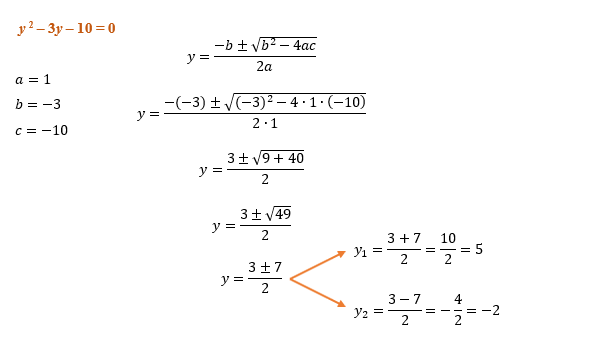
De posse das raízes da equação, y₁ = 5 e y₂ = –2, podemos retornar a igualdade que foi dada pela transformação de variável, para enfim utilizarmos os conceitos de módulo em si. Como são duas raízes, teremos duas igualdades para analisar, do jeito que aparece na imagem abaixo:

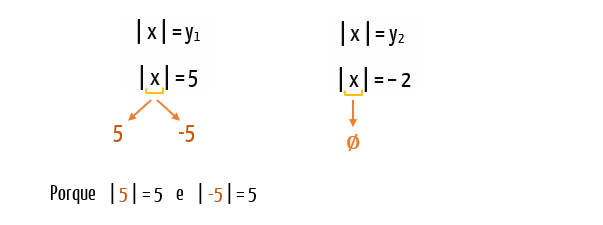
Quando afirmamos que módulo de x é igual a 5, significa que x pode assumir tanto o valor 5 como o valor oposto a ele, – 5, já que tanto módulo de 5, quanto de – 5 são iguais a 5. Agora, quando afirmamos que módulo de x é igual a – 2, instaura-se um problema! Isso porque jamais o módulo de um número real poderá resultar em um valor negativo. Para tanto, não existem valores de x que tornem a segunda igualdade verdadeira, de forma que o conjunto solução da equação é dado apenas por:

S = {– 5, 5}

Pessoal, lembrem que a maioria das equações do segundo grau possui uma raiz positiva e outra negativa. Por isso, fiquem atentos! Casos como o que acabamos de resolver são muito comuns nas equações modulares.

 

2. | x² – x – 1 | = 1

Neste caso, fica ainda mais evidente que iremos resolver uma equação modular, afinal, toda uma expressão algébrica encontra-se dentro de módulos. Em situações como essa, a resolução consiste em utilizarmos diretamente o conceito de módulo que vimos no quadro logo no início do texto.

Se o módulo de uma expressão algébrica do 2º grau é igual a 1, então essa expressão poderá resultar no próprio valor 1, ou ainda no valor oposto a ele, que é – 1. Tanto módulo de 1 quanto módulo de – 1 são iguais a 1. Assim, nosso trabalho será encontrar os valores de x que fazem com que a expressão do exemplo seja igual a 1, e também os valores de x que fazem com que a mesma seja igual a – 1.

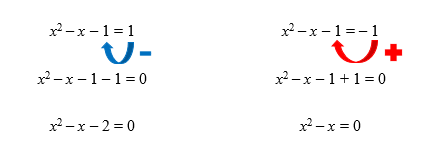
Vejam que para cada um dos casos, foi obtida uma equação do 2º grau diferente. Assim, se encontrarmos as raízes de ambas as equações, teremos o conjunto solução da equação modular como um todo. Vamos optar agora, por determinar as raízes da primeira equação, x² – x – 2 = 0, através do método da soma e produto, mas é claro que vocês poderiam utilizar a fórmula de Bhaskara também, do jeito que fizemos antes.

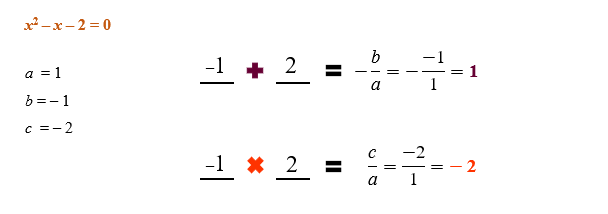
Encontradas as raízes da primeira equação, x₁ = – 1 e  x₂ = 2, vamos a resolução da segunda equação, x² – x = 0. Esse é um exemplo de equação do 2º grau incompleta, e equações como essa podem ser resolvidas sem uso da fórmula de Bhaskara ou mesmo do método da soma e produto, olhem só:

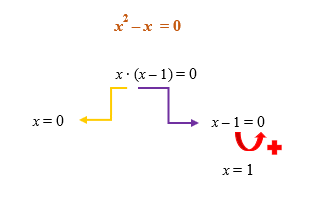
De posse das duas raízes da equação x² – x = 0, x₁ = 0 e  x₂ = 1, já podemos montar o conjunto solução da equação modular como um todo:

S = {– 1, 0, 1, 2}

Então pessoal, existem diferenças cruciais entre o primeiro e o segundo exemplo que acabamos de estudar. No primeiro exemplo, as raízes obtidas da equação do 2º grau eram igualadas ao módulo de x, ou seja, eram o resultado do módulo de x. E o resultado do módulo de qualquer número real jamais pode ser negativo, por isso a raiz negativa não gerou solução alguma. Contudo, no segundo exemplo que resolvemos, buscamos por valores que ao substituírem a variável x, faziam com que a expressão dentro do módulo resultasse em valores cujo módulo deveria ser igual a 1. Tomem cuidado com as diferenças entre os valores que podem estar dentro do módulo, e os valores que podem ser o resultado de um módulo!

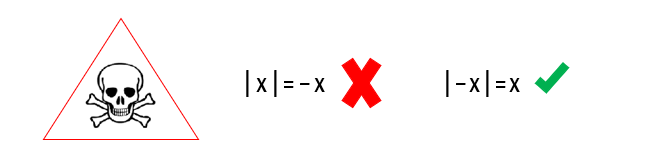
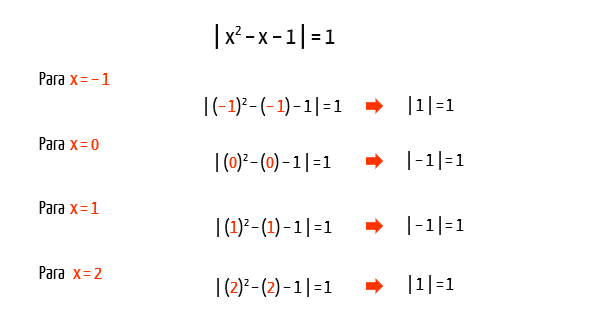
Beleza, pessoal? Fiquem atentos ao próximo exemplo que vamos resolver.

 

3. | x² | – 7x – 8 = 0

Mas que coisa esquisita! Apesar de termos uma das incógnitas da equação dentro de módulos, o que caracteriza uma equação modular, esse é justamente o problema do caso: só uma das incógnitas está dentro do módulo!!! Bem louco, não é mesmo? Mas a verdade é que não há motivos para se assustar. Podemos matar a charada facilmente utilizando uma das propriedades do módulo:

De acordo com essa propriedade, o módulo de x² resultará sempre no mesmo valor que o próprio x² em si. Sendo assim, não há motivos que nos impeçam de realizar a seguinte substituição:

| x² | = x²

| x² | – 7x – 8 = 0   ⟹  x²  – 7x – 8 = 0

Ou seja, nesse caso a solução da equação modular | x² | – 7x – 8 = 0, é exatamente a mesma da equação do 2º grau x²  – 7x – 8 = 0, porque ambas são equivalentes segundo uma das propriedades do módulo. Então, nada de perder tempo! Vamos encontrar as raízes dessa equação através da fórmula de Bhaskara, e na sequência, já teremos em mãos o conjunto solução da equação modular.

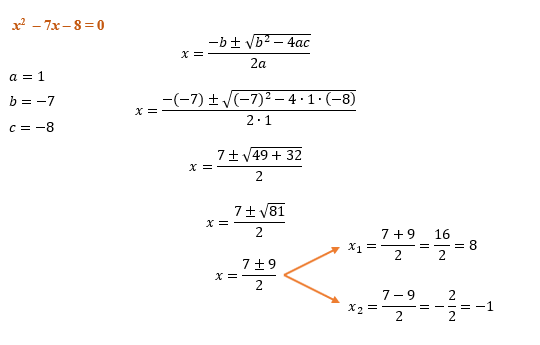
S = {– 1, 8}

 

4. x² + 3| x | – 18 = 0

Por essa vocês não esperavam, não é mesmo? Temos um caso muito semelhante ao anterior, em que apenas uma das incógnitas se encontra dentro de módulos, o que não deixa dúvidas de que a equação é mesmo modular. Agora, o que fazer se o módulo se encontra na incógnita x e não na x²? Não teríamos mais como utilizar a propriedade do módulo que acabamos de ver?

Pessoal, aquela propriedade parece simples, mas a verdade é que ela nos disponibiliza uma série de recursos que tornam possível a resolução de diversas equações modulares. Se nós podemos afirmar que | x² | = x², então por que não poderíamos afirmar que x² = | x² |, ou melhor ainda, que x² = | x |²?

x² = | x |²

x² + 3| x | – 18 = 0    ⟹    | x |² + 3| x | – 18 = 0   

Desta forma, a resolução da equação estaria garantida através da técnica que aplicamos no primeiro exemplo, a chamada transformação de variável.

| x | = y

| x |² + 3| x | – 18 = 0   

y ² + 3y – 18 = 0   

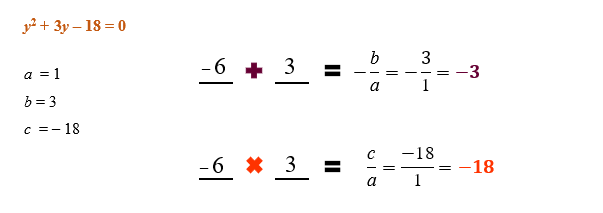
Através do método da soma e produto, as raízes da equação y ² + 3y – 18 = 0 se tornaram conhecidas: y₁ = – 6  e y₂ = 3. Assim, para obtermos as soluções da equação modular como um todo, devemos retornar a igualdade que representa a transformação de variável.

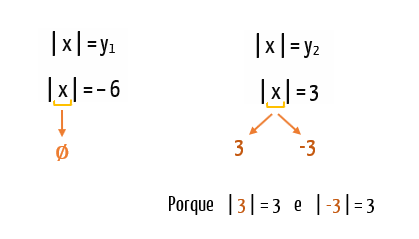
Novamente, o fato do módulo de qualquer número real não poder resultar em um valor negativo, fez com que apenas uma das igualdades fosse válida, | x | = 3. Neste caso, tanto 3 quanto – 3 podem assumir o lugar de x, afinal tanto módulo de 3 quanto módulo de –3 são iguais a 3. Enfim chegamos ao conjunto solução da equação:

 S = {– 3, 3}

E aí, pessoal, o que acharam deste texto? Depois de todas essas informações, é fato que ele está chegando ao fim. Mas não se preocupem, logo estou aí de volta! Continuem estudando bastante matemática e assistam o vídeo que está em anexo, afinal uma abordagem sempre complementa a outra!

Um abração! Bons estudos a todos!