CONDIÇÃO DE EXISTÊNCIA DOS LOGARITMOS

Olá pessoal! Tudo bem por aí?

Quem conhece os logaritmos, sabe que dois de seus três termos possuem algumas restrições quanto aos valores numéricos que podem assumir. Se a base de um logaritmo não for um valor maior que zero e diferente de 1, ou se o logaritmando desse mesmo logaritmo não for um valor positivo, então o logaritmo não poderá existir. Por isso, quando a base e/ou o logaritmando de um logaritmo for formado por uma expressão algébrica, seja ela de 1º ou de 2º grau, nós devemos garantir que essa expressão resulte em valores dentro da faixa que torna possível a existência do logaritmo!

Complicado, pessoal? É, alguns alunos têm mais dificuldade com os logaritmos, outros com probabilidade, outros com geometria, e pode até haver alunos que não se adaptem a boa parte da matemática do ensino médio. Mas isso não é um problema, acreditem! Com muita dedicação, esforço e contando com ótimos materiais de estudo, a matemática fica simples, pessoal! É isso que o Professor Ferretto quer lhes mostrar em sua plataforma de estudos! Só lá, ele disponibiliza o conteúdo completo da matemática do ensino médio, com aulas didáticas e mais de 1000 exercícios do ENEM e dos vestibulares resolvidos em vídeo, para vocês praticarem bastante todo o conhecimento adquirido. Querem tirar uma nota ótima no ENEM e nos vestibulares logo mais? Então acessem o site, e confiram os demais benefícios do curso!

Depois dessa dica maravilhosa, nada melhor do que entendermos direitinho essa história de um logaritmo existir ou não. Nós vimos no texto Introdução aos Logaritmos, que os termos dos logaritmos possuem a seguinte nomenclatura:

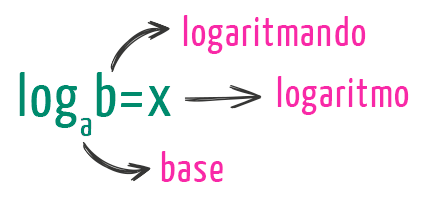
Além disso, nós também vimos por lá duas retas reais muito interessantes, que nos mostravam a região de valores que a base a e o logaritmando b poderiam assumir para que sua existência fosse garantida:

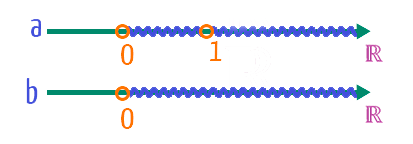
Pois bem, pessoal, a ideia é simples: se a base a de um logaritmo for maior que zero e diferente de 1 (0 < a ≠ 1), e se o logaritmando b também for um valor maior que zero ou positivo, então o logaritmo terá sua existência garantida. Caso vocês queiram entender mais a fundo porque essas restrições existem, é só estudar a definição de função exponencial, afinal, foi ela que deu origem ao conceito de logaritmo. Nosso objetivo aqui, no entanto, é simplesmente adotar essas restrições como verdade, e garantir que logaritmos como esses, apresentados na imagem abaixo, possam existir!

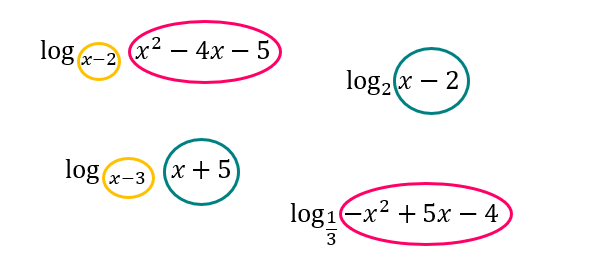
Observem que os logaritmos que acabaram de ser apresentados possuem expressões algébricas ocupando o lugar dos seus logaritmandos, e o lugar de suas bases em alguns casos também. Como tanto a base, quanto o logaritmando de um logaritmo devem ser valores maiores do que zero, nosso trabalho será obter os valores de x que tornem essas expressões maiores do que zero ou positivas. Aí, quando se tratar de uma expressão que esteja localizada no valor da base do logaritmo, nós também deveremos tomar cuidado para que os valores de x encontrados sejam diferentes de 1.

Tranquilo, não é mesmo? Como as expressões de que estamos falando são do 1º e do 2º grau, é muito importante que vocês saibam tudo sobre as inequações do 1º grau, e claro, sobre as inequações do 2º grau também! Mas não se preocupem, a ideia ficará muito mais clara a partir de agora, pois vamos resolver uma série de exemplos que envolvem o assunto! Sigam comigo aqui!

 

1. Determine os valores de x para os quais existe:

a. log ₂ (x – 2)

O primeiro detalhe em que devemos prestar atenção aqui, é no valor que a base do logaritmo está assumindo. Vejam que está tudo dentro dos conformes, afinal, 2 é um valor maior que zero e diferente de 1(0 < 2 ≠ 1). Já em relação ao logaritmando, nós ainda não podemos dizer a mesma coisa. Isso porque ele é formado por uma expressão algébrica do 1º grau, e para que o logaritmo exista, esta deve resultar em um valor maior que zero. Portanto, para descobrirmos os valores de x que tornam a expressão maior do que zero, nós iremos resolver a seguinte inequação do 1º grau:

x – 2 > 0

x > 2

Qualquer valor maior que 2 que substitua o lugar de x no logaritmo, faz com que o mesmo exista. Por isso o conjunto solução para o caso é o seguinte:

S = { x ∈ ℝ | x > 2}

 

b. log _⅓ (– x² + 5x – 4)

Novamente, em relação a base do logaritmo não há motivos para se preocupar, afinal, ⅓ é um valor maior que zero e diferente de 1 (0 < ⅓ ≠ 1). Por sua vez, no logaritmando deste mesmo logaritmo, surgiu uma expressão algébrica do 2º grau, e assim, será necessário encontrarmos os valores de x que tornam essa expressão maior do que zero ou positiva. Só desta forma é que a existência do logaritmo estará garantida!

As inequações do 2º grau permitem que se descubra os valores de x que tornam qualquer expressão do 2º grau maior do que zero. Só que elas costumam ser resolvidas através do estudo do sinal da função quadrática, portanto, não vai ter jeito, vamos ter que fazer isso agora. Assim, quem nunca ouviu falar no assunto, deve dar uma olhadinha no texto Aplicando o estudo do sinal de uma função do 2º grau antes de continuar essa leitura!

– x² + 5x – 4 > 0

Feito, pessoal? Então vocês já sabem que o primeiro passo consiste em transformar a expressão do segundo grau em uma função f(x). Na sequência, já podemos obter os seus coeficientes a, b, e c, e determinar a concavidade da parábola que será formada:

f (x) = – x² + 5x – 4

a = – 1

b = 5

c = – 4

Como o valor numérico de a é negativo ou menor que zero (– 1 < 0), a concavidade da parábola formada será voltada para baixo! Agora, vamos calcular o discriminante da função do 2º grau (∆), e assim determinaremos a natureza das raízes desta função.

Δ = b² – 4ac

Δ = 5² – 4 ∙ (– 1) ∙ (– 4)   

Δ = 25 – 16

Δ = 9 → Δ > 0

Neste momento, nós já temos conhecimento de que as duas raízes da função f (x) são reais e distintas (x₁ ≠ x₂), o que permite que a parábola formada corte o eixo x em dois pontos diferentes! Só nos resta descobrir então, o valor numérico dessas raízes, e na sequência, teremos condições de esboçar o gráfico da função para estudar o seu sinal efetivamente.

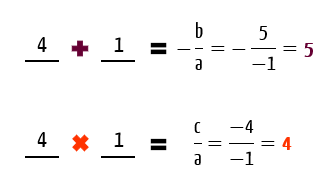
Através do método da soma e produto, foi possível determinar que as raízes da função f (x) são x₁ = 4, e x₂ = 1. É claro que vocês poderiam ter obtido esses mesmos valores utilizando a fórmula de Bhaskara, sem problema algum!

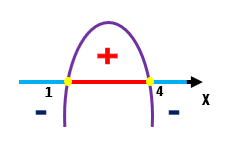
Nós estamos interessados apenas nos valores de x que tornam a função positiva, ou seja, maior do que zero. Tendo isso em vista, e observando o esboço do gráfico da função apresentado acima, é fato que a parábola só se encontra acima do eixo x para os valores de x que se situam entre 1 e 4. Por isso, apenas esses valores farão parte da solução da inequação.

S = { x ∈ ℝ | 1 < x < 4}

Assim, se a incógnita x localizada no logaritmando de log _⅓ (– x² + 5x – 4) for substituída por qualquer valor real que estiver entre 1 e 4, então o logaritmo poderá existir! Do contrário, ou seja, se qualquer valor menor que 1, maior que 4, ou mesmo os próprios 1 e 4 substituírem a incógnita x do logaritmando, então o logaritmo não irá existir!

 

c. log _{x – 3} (x + 5)

Opa! Chegamos a um caso onde tanto a base quanto o logaritmando do logaritmo são formados por expressões algébricas de 1º grau. Por isso, precisaremos garantir que tanto a expressão x – 3, quanto a expressão x + 5 resultem em valores maiores do que zero. Além disso, é importante lembrar que a expressão que se encontra no lugar da base, x – 3, também não poderá resultar em um valor igual a 1!

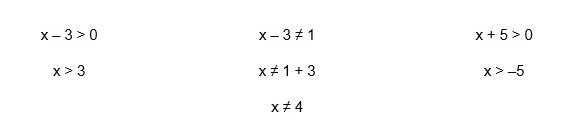
As inequações do 1º grau apresentadas acima, nos mostram uma solução que satisfaz apenas a base do logaritmo (3 < x ≠ 4), e outra solução que satisfaz apenas o logaritmando desse mesmo logaritmo (x > – 5 ). Mas a verdade é que estamos em busca de uma única solução que satisfaça o logaritmo como um todo, e para que possamos ter essa solução conjunta, ou seja, uma solução que seja adequada para ambos os termos, deveremos realizar a intersecção entre as duas soluções já existentes.

Esse processo consiste basicamente em desenharmos 3 retas reais, que representam, respectivamente, os valores de x que fazem parte da solução do logaritmando (b), os valores de x que fazem parte da solução da base (a), e finalmente, os valores de x que fazem parte do conjunto solução geral.

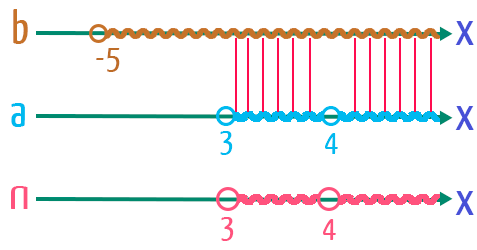
Já que os únicos valores de x que satisfazem tanto a base, quanto o logaritmando do logaritmo são aqueles maiores do que 3 e diferentes de 4, o conjunto solução para o caso pode ser dado da seguinte maneira:

S = { x ∈ ℝ | x > 3 e x ≠ 4}

E agora, para finalizarmos o texto, vamos a um exemplo muito interessante. Acompanhem com atenção!

 

d. log _{x – 2} ( x² – 4x – 5)

Mais uma vez, tanto a base quanto o logaritmando do logaritmo são formados por expressões algébricas, só que agora uma é de 1º grau, x – 2, e a outra é de 2º grau, x² – 4x – 5. Assim, resta-nos resolver inequações do 1º e do 2º grau, afim de garantirmos que ambas as expressões sejam positivas ou maiores do que zero, sem esquecermos, é claro, que a expressão que representa a base do logaritmo, x – 2, também não pode resultar em um valor igual a 1.

Já temos a solução que satisfaz a base do logaritmo (2 < x ≠ 3), mas para obtermos a solução que satisfaz o seu logaritmando, vamos precisar realizar mais um estudo do sinal da função quadrática. Vem comigo aqui!

x² – 4x – 5 > 0

f(x) = x² – 4x – 5

a = 1

b = – 4

c = – 5

Neste caso, a concavidade da parábola formada será voltada para cima, afinal, o valor do coeficiente a da função f(x) é maior do que zero (1 > 0). Na sequência, vamos ao cálculo do discriminante (∆) da função.

Δ = b² – 4ac

Δ = (– 4)² – 4 ∙ 1 ∙  (– 5)

Δ = 16 + 20

Δ = 36 → Δ > 0

O cálculo do discriminante acabou de nos provar que essa função também possui duas raízes reais e distintas (x₁ ≠ x₂), o que permite que a parábola formada corte o eixo x em dois pontos diferentes! E agora, afim de descobrirmos o valor numérico dessas duas raízes, nós utilizaremos a famosa fórmula de Bhaskara. É claro que quem desejar, pode resolver a questão através do método da soma e produto, como fizemos anteriormente.

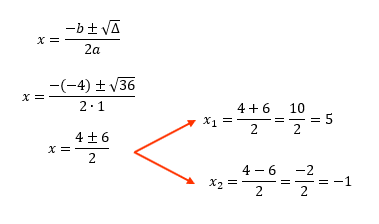
Feito isso, vamos ao esboço do gráfico da função f(x) = x² – 4x – 5:

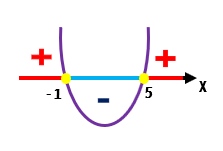
Observando o esboço acima, é possível perceber que para valores de x menores do que – 1 e maiores do que 5, a parábola se encontra acima do eixo x, o que nos permite concluir que nesse caso a função é positiva, ou maior do que zero, do jeito que queríamos (x² – 4x – 5 > 0). Portanto, esses valores de x fazem parte da solução da inequação do 2º grau:

S = { x ∈ ℝ | x < –1 e x > 5}

Mas, calma! Não podemos esquecer que essa solução satisfaz apenas o logaritmando do logaritmo. Precisaremos realizar novamente a intersecção das duas soluções que encontramos, a fim de determinarmos uma única solução que satisfaça o logaritmo como um todo.

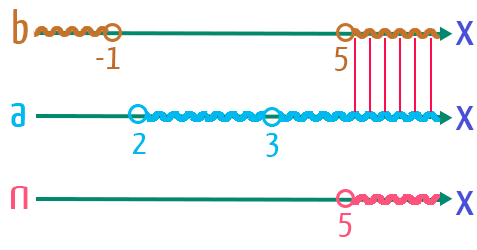
Vejam na imagem acima, que apenas valores maiores do que 5 são comuns a ambas as soluções, e portanto, satisfazem o logaritmo como um todo. Por isso, o conjunto solução final, é dado a seguir:

S = { x ∈ ℝ | x > 5}

 

Beleza, pessoal? Pois é, lá se foi mais um texto sobre os logaritmos! Espero que esse assunto tenha sido proveitoso para os estudos de vocês, e que sirva de exemplo para que vocês obtenham a condição de existência dos mais diversos logaritmos que surgirem! E aí já aproveito para reforçar dois pontos importantes: o primeiro, é que apesar de não termos resolvido nenhum caso por aqui, podem existir logaritmos aonde apenas a base é formada por uma expressão algébrica, e aí basta resolvê-la tomando os cuidados que nós aprendemos hoje. O segundo ponto importante, é que quando base e logaritmando são formados por expressões algébricas, não dá para esquecer de fazer a intersecção das duas soluções!

Entendido? Então eu fico por aqui! Vale a pena assistir o vídeo que está em anexo, afinal, ele complementa tudo que acabou de ser visto. E não esqueçam: tem muita matemática a ser explorada aqui no blog. Acompanhem novas postagens a cada semana!

Abração! Vejo vocês em breve!