NÚMEROS RACIONAIS
05/07/2019
Todos os números que podem ser escritos na forma de fração são considerados números racionais. Por isso, esse conjunto numérico compreende os números naturais, inteiros, decimais exatos e também as dízimas periódicas.
Olá, pessoal! Tudo bem?
Se vocês chegaram até aqui hoje, é porque desejam saber tudo sobre os números racionais. Pois vieram ao lugar certo! Vamos falar neste texto, sobre a origem e a definição do conjunto dos números racionais, além de sua relação com a média aritmética.
Beleza, pessoal? Sendo assim, peguem todos os seus materiais de estudo porque nós vamos começar. Vem comigo!
1. ORIGEM DOS NÚMEROS RACIONAIS

Cada um dos conjuntos numéricos que conhecemos hoje surgiu diante da necessidade de representar uma certa quantidade de algo. É claro que não foi diferente com os números racionais. Até então, existiam apenas os números naturais e os números inteiros, mas nenhum deles conseguia representar as partes de um todo. Por exemplo, digamos que você e seus amigos estivessem comendo uma deliciosa pizza, e sobrassem 2, de um total de 8 pedaços. Sem a existência dos números racionais, vocês jamais poderiam dizer que sobrou ¼ de pizza!
Além disso, uma das 4 operações fundamentais da aritmética também não estava totalmente satisfeita sem a existência dos números racionais. Quando somamos, subtraímos ou multiplicamos dois números inteiros, sempre obtemos como resultado números também inteiros. Contudo, caso uma divisão entre dois números inteiros seja realizada, o resultado pode ser inteiro, mas também decimal. Ops! Números decimais nunca fizeram parte do conjunto dos números inteiros. É dessa ideia que surgiu a definição dos números racionais, a qual vamos conhecer no próximo item. Sigam comigo!
2. DEFINIÇÃO DO CONJUNTO DOS NÚMEROS RACIONAIS

O conjunto dos números racionais, representado pelo símbolo ℚ, é descrito como o conjunto dos quocientes entre dois números inteiros a e b.
Nós acabamos de descobrir que o conjunto dos números racionais surgiu com o intuito de abranger os resultados das operações de divisão entre dois números inteiros que não geram números também inteiros. Por esse motivo, qualquer número que possa ser representado na forma de uma divisão, de quociente, de razão ou de fração, é um número racional. Só que toda divisão ou fração possui uma restrição: seu divisor ou denominador jamais pode ser igual a zero, ou nulo! É isso que veremos agora na definição do conjunto dos números racionais por propriedade:

O conjunto dos números racionais é formado por todo quociente entre dois números a e b, tais que o numerador a pertença ao conjunto dos números inteiros, e que o denominador b pertença ao conjunto dos números inteiros não nulos. Se vocês derem uma olhadinha no texto Números Naturais e Inteiros, poderão perceber que lá se fala muito no significado do asterisco juntamente ao símbolo de um conjunto. Se o asterisco está presente, é um sinal de que o elemento zero não pertence ao conjunto. Justo, afinal, eu repito: o denominador de uma fração jamais pode ser zero.
E aí, o que acharam desta definição? Como sempre, exemplos numéricos tornam tudo bem mais claro. Seguem abaixo alguns números racionais:


Pessoal, todo número natural ou inteiro também é considerado um número racional. Isso porque é possível representar cada um deles na forma de fração, como manda a definição. Qualquer número dividido por 1, resulta nele mesmo. Portanto, uma das formas de escrever os números naturais e inteiros na forma de fração é utilizando como denominador o número 1!
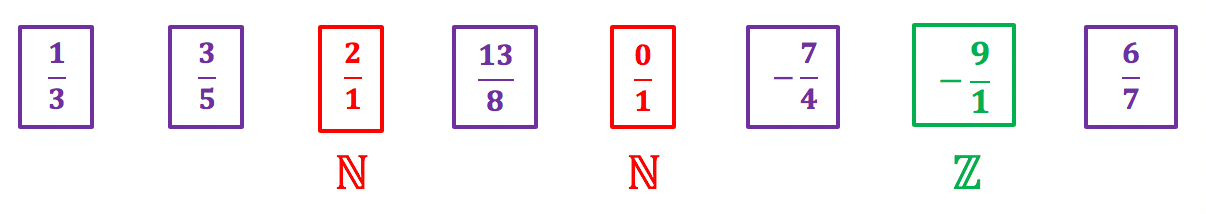
2.1 A relação entre os números naturais, inteiros e racionais
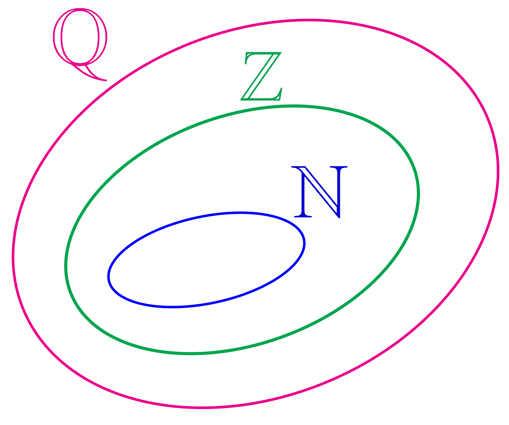
O fato de representarmos os números naturais e inteiros na forma de fração, jamais fará com que eles deixem de pertencer ao seu conjunto numérico de origem. Muito pelo contrário. Lembrem que o conjunto dos números naturais é subconjunto dos números inteiros, porque todo elemento que pertence ao conjunto dos números naturais também pertence ao conjunto dos números inteiros. Ora, se todo número inteiro pode ser representado na forma de fração, então o conjunto dos números inteiros é subconjunto do conjunto dos números racionais.
É isso que podemos visualizar no diagrama da imagem acima. Sob um segundo ponto de vista, também é possível dizer que o conjunto dos números racionais compreende o conjunto dos números inteiros, que por sua vez, compreende o conjunto dos números naturais!
Tranquilo até aqui? Bom, nós já definimos os números racionais, falamos que os números naturais e inteiros também são racionais, mas ainda não entramos em detalhes sobre os números que são exclusivamente racionais. São os números decimais, aqueles que representam a parte de um todo. Vem comigo!
2.2 As frações e sua representação decimal

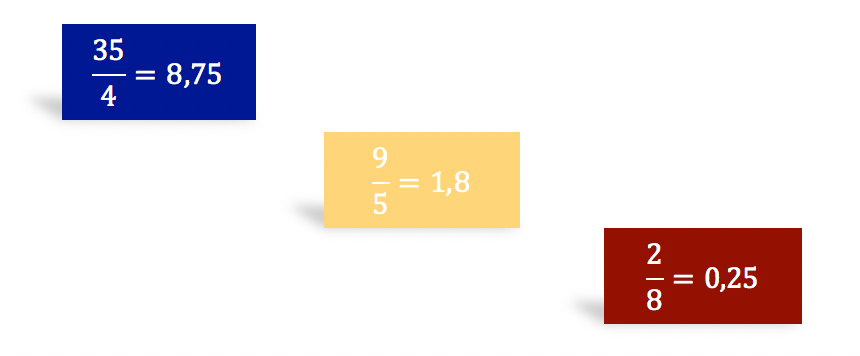
Apenas dois tipos de números decimais pertencem ao conjunto dos números racionais: os decimais exatos e os periódicos. Os primeiros, são aqueles que possuem um número finito de casas decimais não nulas. Abaixo, seguem alguns exemplos de frações que resultam em números decimais exatos.
Já os decimais periódicos, possuem uma definição totalmente contrária a que acabamos de aprender. Estes números contêm infinitas casas decimais não nulas. Contudo, aí mora um detalhe importante: são casas decimais infinitas, mas não aleatórias. Os decimais periódicos são chamados assim, porque os números que compõem suas casas decimais se repetem, ou seja, tem periodicidade.
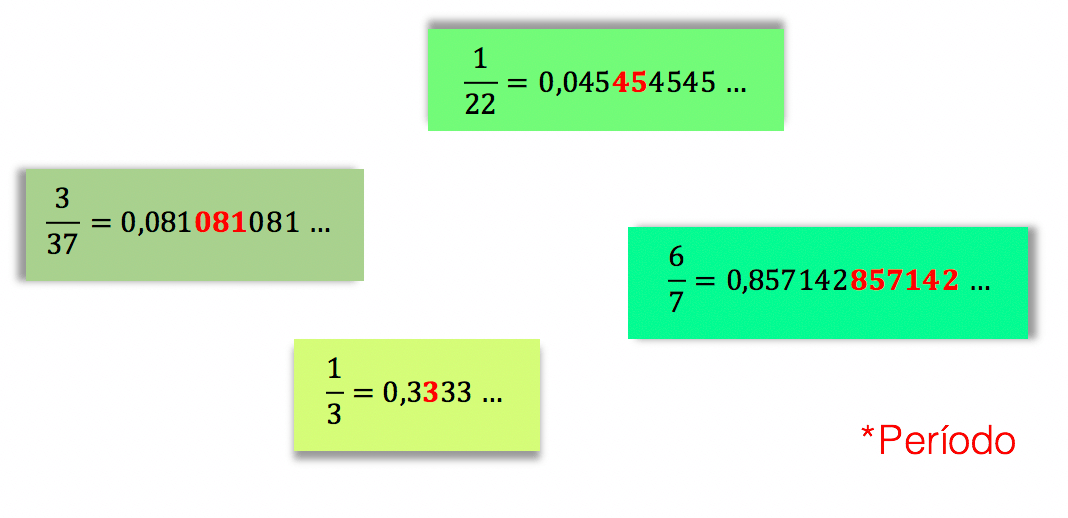
E aí, gostaram destes exemplos? Para quem achou os números familiares, sim, os decimais periódicos também são conhecidos como dízimas periódicas! Se vocês quiserem saber mais sobre elas, é só acessar este texto aqui.
Certo, pessoal? Agora que definimos todos os elementos que pertencem ao conjunto dos números racionais, partiremos para o último item do texto. Abordaremos brevemente uma peculiaridade dos números racionais. Vamos lá!
3. OS NÚMEROS RACIONAIS E A MÉDIA ARITMÉTICA

Para entendermos qual é a relação entre os números racionais e a média aritmética, nós vamos dispor alguns valores em uma reta real. Começaremos pelos números naturais e inteiros.
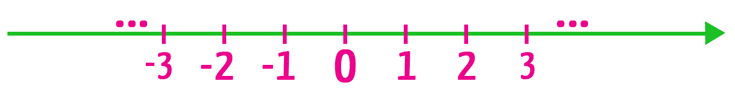
No texto de hoje, nós descobrimos que em meio aos números dispostos acima, existem aqueles que representam as partes de um todo. São as frações, que também podem ser escritas como números decimais exatos ou como dízimas periódicas. Vamos inserir na reta real alguns destes novos números, como por exemplo, a fração – 4/3 e a fração ½. A primeira delas se localiza entre os números inteiros –2 e –1, e a segunda se localiza entre os números naturais e inteiros 0 e 1.

E se agora nós desejássemos completar a reta real com diversos valores racionais, ou frações. Vocês saberiam dizer como poderíamos obter esses infinitos valores? É aí que mora o segredo pessoal. Entre dois números racionais, sempre haverá um terceiro número racional, e para conhecê-lo, basta aplicar uma média aritmética aos valores.
Querem ver como dá certo? Então sigam comigo rumo a um exemplo!
3.1 Exemplo resolvido sobre a relação entre os números racionais e a média aritmética
Dada a seguinte reta real, obtenha o número racional que se encontra entre os demais.
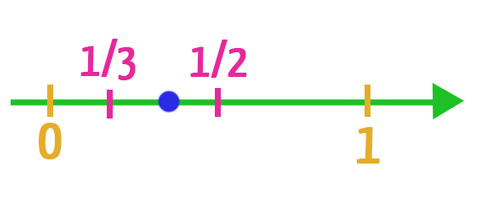
Para fazer isso, vamos aplicar a média aritmética aos números 1/3 e 1/2. Quem ainda não conhece a fórmula desta operação, pode conferi-la na imagem do item 3, quando o cálculo é realizado entre dois termos. Vamos lá!
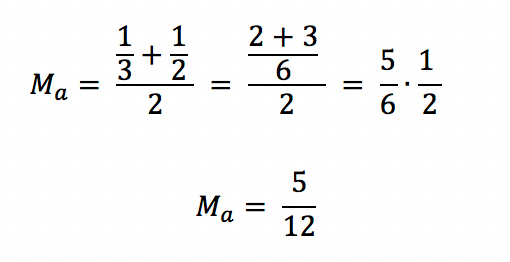
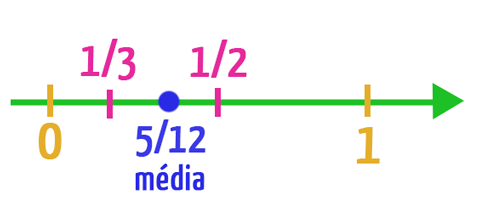
Assim, caso desejássemos complementar essa reta real, e incluir uma série de pontos entre 1/3 e 5/12, ou entre 5/12 e 1/2, por exemplo, nós realizaríamos uma média aritmética entre eles, e em seguida, uma série de novas médias aritméticas, até que fosse possível atingir o nosso objetivo.
Interessante, não é mesmo? É com esse assunto que encerramos o texto de hoje! Espero que vocês tenham aprendido bastante, e que os conceitos vistos aqui facilitem os seus estudos em matemática e em outras áreas afins. Não será uma má ideia dar uma olhadinha no vídeo que deixo em anexo. Como de costume, ele complementa todas as informações que nós acabamos de estudar!
Gostou deste conteúdo? Clique aqui para saber como a Plataforma do Professor Ferretto funciona!
Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da Plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!
Abração! Nos vemos em breve!