
Os assuntos de biologia que mais caem no Enem sûÈo uma das preocupaûÏûçes de quem estûÀ se preparando para a...

Vocûˆ conhece as definiûÏûçes de subconjunto, conjunto das partes, conjuntos iguais e conjuntos disjuntos? Clique aqui e aprenda comigo tudo sobre estes conceitos da teoria dos conjuntos!
Um conjunto pode ser dito subconjunto de outro, quando todos os seus elementos tambûˋm fazem parte deste outro conjunto. O conjunto das partes, por sua vez, ûˋ um conjunto formado por todos os subconjuntos de um conjunto de referûˆncia.
OlûÀ, pessoal! Tudo bem?
No texto de hoje, nû°s estudaremos mais dois conceitos muito importantes dentro da teoria de conjuntos: osô subconjuntosô e oô conjunto das partes! Vamos aproveitar para falar tambûˋm sobre os conjuntos iguais, os conjuntos disjuntos, e sobre as propriedades da inclusûÈo. Se vocûˆs nûÈo conhecem esses termos, ou nûÈo entenderam com clareza as definiûÏûçes acima, nûÈo deixem de acompanhar o texto com atenûÏûÈo! Tenho certeza de que este conteû¤doô os ajudarûÀ a resolver com facilidade as questûçes de conjuntos das provas do ENEMô e dos vestibulares!
Preparados? Peguem seus materiais de estudo porque agora nû°s vamos comeûÏar!

Um conjunto A ûˋ subconjunto de um conjunto B se todo elemento de A ûˋ tambûˋm elemento de B.
Em outras palavras, podemos dizer que um certo conjunto A ûˋ subconjunto de um conjunto B, se todos os elementos que pertencem û A, tambûˋm pertencerem ao conjunto B. Vamos fazer um exemplo para entender bem essa ideia.

Dados os conjuntos C = {8, 9, 10, 11}, D = {9, 11}, e E = {6, 9, 12}.
a. D ûˋ subconjunto de C?
Sim, D ûˋ um subconjunto do conjunto C! Observem que todos os elementos do conjunto D tambûˋm pertencem ao conjunto C.
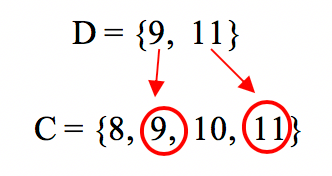
No texto IntroduûÏûÈo aos Conjuntos, nû°s aprendemos que tambûˋm podemos representar os conjuntos atravûˋs de diagramas. Olhem sû° como ûˋ realizada a representaûÏûÈo em forma de diagrama dos conjuntos C e D:
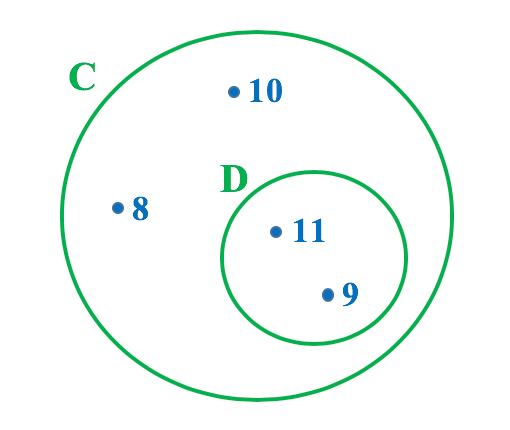
E nûÈo ûˋ que nessa representaûÏûÈo o conjunto D fica localizado dentro do conjunto C? Pessoal, sempre que o diagrama de um conjunto puder ser representado dentro do diagrama de outro, podem ter certeza que vocûˆs estûÈo diante de um subconjunto!
Bom, se D ûˋ subconjunto de C, tambûˋm podemos dizer que D ã C, ou que D estûÀ contido em C. Na verdade, esse sûÙmbolo matemûÀtico pode ser interpretado de 3 maneiras diferentes, como mostra a figura abaixo:
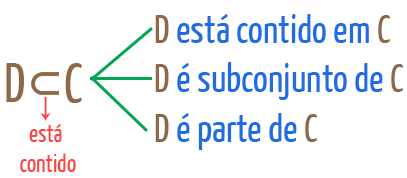

Pessoal, o sûÙmbolo ã significa ãestûÀ contidoã, mas se nû°s o invertermos horizontalmente, teremos o sûÙmbolo ã, que significa ãcontûˋmã. AûÙ a ideia ûˋ exatamente oposta. Contûˋm, no dicionûÀrio, ûˋ dito como ãobjeto que em seu interior possui alguma coisaã. û interessante percebermos, no diagrama que montamos lûÀ em cima, que C possui em seu interior o conjunto D. Por isso, o correto, nesse caso, ûˋ dizer que C contûˋm D.

Entendido? Vamos observar um contexto um pouquinho diferente na prû°xima questûÈo.
b. E ûˋ subconjunto de C?
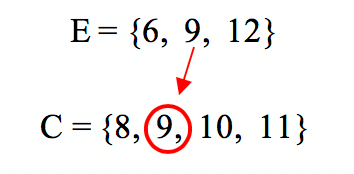
Neste caso, apenas um elemento do conjunto E tambûˋm pertence ao conjunto C. Por isso, E nûÈo ûˋ subconjunto de C, sob hipû°tese alguma. Mas quando apenas alguns elementos sûÈo comuns a dois conjuntos, tambûˋm ûˋ possûÙvel realizar uma representaûÏûÈo do caso em forma de diagrama.ô
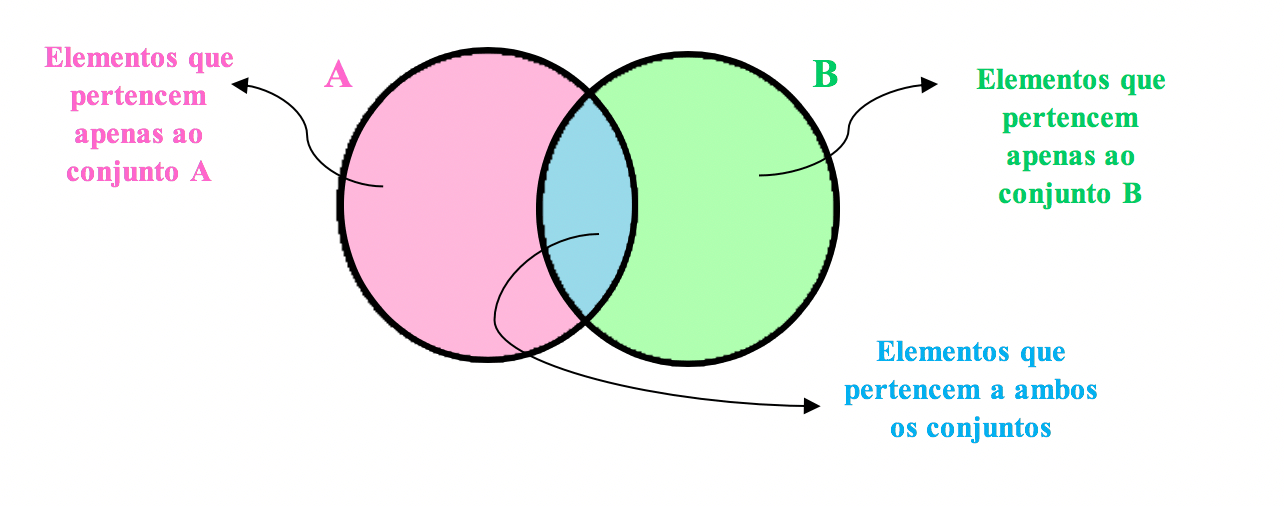
Percebam que para realizar a representaûÏûÈo em forma de diagrama de dois conjuntos que possuem apenas alguns elementos em comum, basta entrelaûÏar os diagramas destes dois conjuntos. Assim, na parte central, que ûˋ comum aos dois diagramas, nû°s inserimos os elementos comuns a ambos os conjuntos. Vamos fazer isso para os conjuntos C e E.
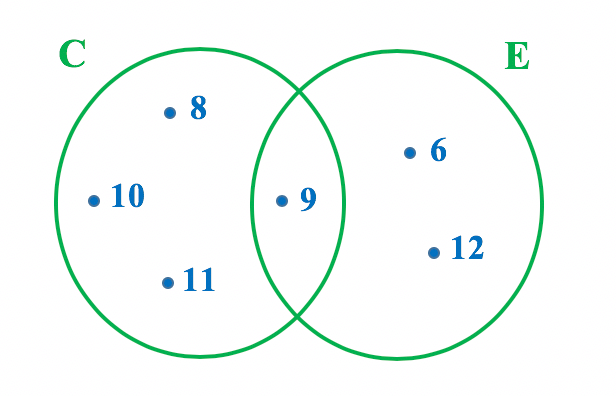
JûÀ que E nûÈo ûˋ subconjunto de C e que nem mesmo C ûˋ subconjunto de E, nû°s utilizamos o sûÙmbolo ã, para relatar que um conjunto ãnûÈo estûÀ contidoã no outro.
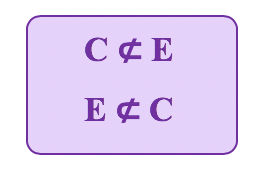
Bom, nû°s jûÀ estudamos atûˋ aqui duas situaûÏûçes interessantes. Na primeira delas, um conjunto ûˋ dito subconjunto de outro, enquanto que na segunda isso jûÀ nûÈo pode ser afirmado, apesar de alguns elementos ainda serem comuns entre dois conjuntos diferentes. Mas o fato ûˋ que tambûˋm existem casosô em queô nûÈo hûÀ nenhum elemento comum entre dois conjuntos, ou ainda, onde todos os elementos de dois conjuntos diferentes sûÈo exatamente os mesmos! Abordaremos esses dois conceitos na sequûˆncia.
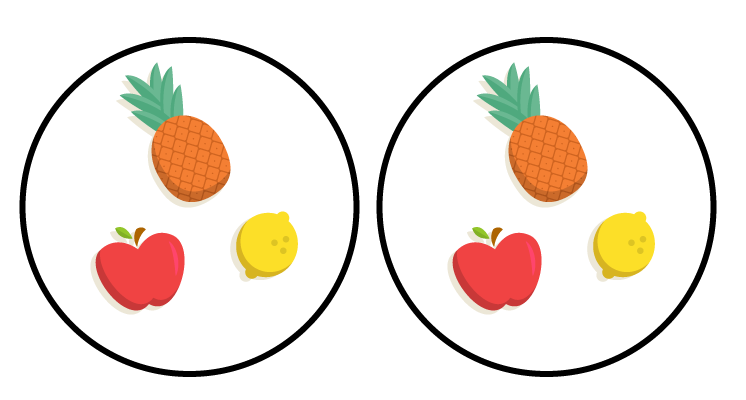
Vamos supor agora uma situaûÏûÈo diferente. Dados dois conjuntos A e B, diremos que B ûˋ subconjunto de A, ou seja, todos os seus elementos tambûˋm pertencem ao conjunto A. Sû° que ao contrûÀrio do que vimos atûˋ entûÈo, adotaremos que A nûÈo tem outros elementos alûˋm daqueles que tambûˋm pertencem a B. Isso significa que A tambûˋm ûˋ subconjunto de B, ou que A estûÀ contido em B, assim como B estûÀ contido em A. Tudo isso nos leva a seguinte conclusûÈo: A e B sûÈo conjuntos iguais!
Dois conjuntos sûÈo iguais quando possuem os mesmos elementos.
Acompanhem os exemplos com atenûÏûÈo:
A = {1, 2}
B = {1, 2}
Aqui nûÈo resta dû¤vida de que A e B sûÈo conjuntos iguais. Assim, sabemos que A estûÀ contido em B assim como B estûÀ contido em A.

C = {a, b, c}
D = {c, b, a}
Observem que nesse caso, apenas a ordem dos elementos foi alterada, mas isso pouco importa. Os conjuntos C e D possuem exatamente os mesmos elementos, a, b e c, e por isso, sûÈo conjuntos iguais.ô
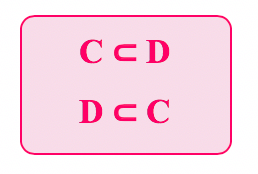
E = {1, 2}
F = {1, 2, 2, 2}
O conjunto F possui elementos repetidos, mas isso tambûˋm nûÈo ûˋ um problema, afinal, de qualquer forma, ambos os conjuntos possuem apenas os elementos 1 e 2. Por isso, E e F sûÈo, sem sombra de dû¤vida, conjuntos iguais.


Dados dois conjuntos A e B, sabe-se que o conjunto A possui alguns elementos, assim como o conjunto B. Sû° que nesse caso, nenhum elemento de A tambûˋm pertence ao conjunto B, da mesma forma que nenhum elemento de B tambûˋm pertence ao conjunto A. Isso significa que nem ao menos podemos entrelaûÏar os diagramas dos dois conjuntos, porque nûÈo hûÀ nada em comum ou igual entre eles. Quando isso acontece, os conjuntos sûÈo ditos disjuntos.
Dois conjuntos sûÈo disjuntos quando nûÈo possuem elementos em comum.
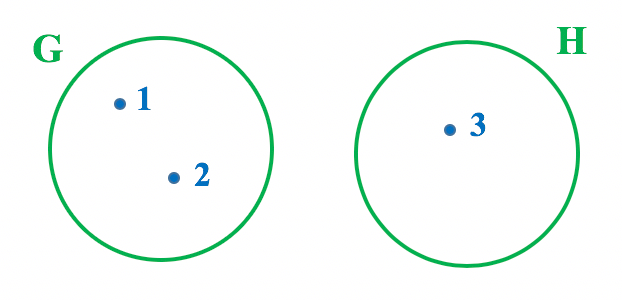
Dados os conjuntos G = {1, 2} e o conjunto unitûÀrio H = {3}, podemos perceber que eles nûÈo possuem elemento algum em comum. G e H sûÈo conjuntos disjuntos, e a sua representaûÏûÈo em forma de diagrama pode ser vista na imagemô abaixo.

Seja um conjunto A, o conjunto das partes de A, representado por P(A), ûˋ o conjunto formado por todos os subconjuntos de A.
Vejam que o conjunto das partes ûˋ um conjunto formado pelas ãpartesã de um conjunto de referûˆncia. Se essa referûˆncia for um certo conjunto A, por exemplo, entûÈo, teremos o conjunto das partes de A, P(A). Mas que partes sûÈo essas? Os elementos de um conjunto das partes, sûÈo, na verdade, outros conjuntos, e mais precisamente sûÈo todos os subconjuntos que podem ser formados a partir dos elementos do conjunto de referûˆncia.
Isso soa bem confuso, nûÈo ûˋ? Por isso, vamos ver atravûˋs de um exemplo, como obter todos os subconjuntos que podem ser formados a partir dos elementos de um determinado conjunto referûˆncia. Vem comigo!
Dado o conjunto A = {1, 2}. Aponte todos os subconjuntos que podem ser formados a partir dos elementos de A.
PoderûÙamos apontar aqui, logo de cara, dois subconjuntos formados pelos elementos do conjunto A: os conjuntos unitûÀrios {1} e {2}. Mas serûÀ que sû° conseguimos montar subconjuntos a partir de combinaûÏûçes diferentes dos elementos de um certo conjunto? û quase isso! Existem duas propriedades que nos mostram que alûˋm dessas combinaûÏûçes, todo conjunto sempre tem dois subconjuntos definidos: sûÈo as propriedades da inclusûÈo.

Atravûˋs das propriedades que acabamos de conhecer, podemos concluir que alûˋm dos dois subconjuntos do conjunto A que jûÀ encontramos, tambûˋm sûÈo subconjuntos de A, o conjunto vazio, e o prû°prio conjunto A.
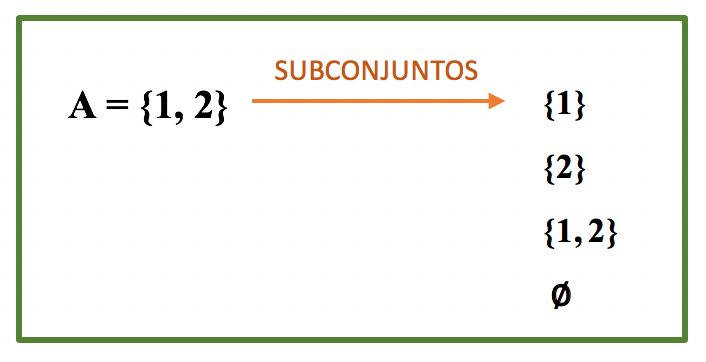
Portanto, podemosô representar o conjunto das partes de A da seguinte maneira:
P(A) = {{1}, {2}, {1, 2}, ã }

Se um conjunto A possui n elementos, entûÈo o nû¤mero de subconjuntos de A ûˋ igual 2n.
Isso explica porque acabamos de encontrar 4 subconjuntos para o conjunto A, afinal 2ôý = 4. Vamos descobrir agora, quantos e quais sûÈo os subconjuntos do conjunto dado abaixo:
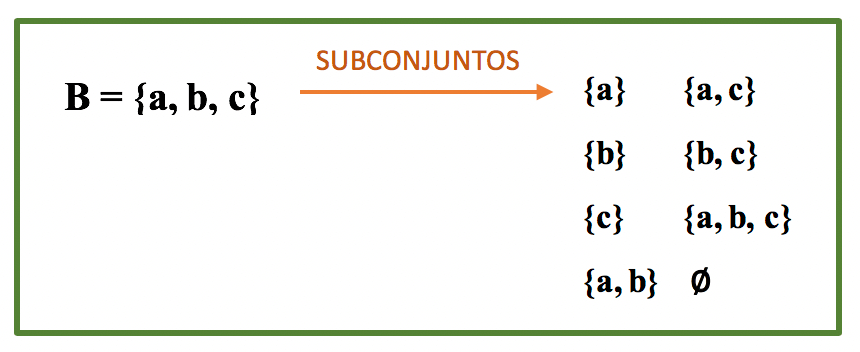
B = {a, b, c}
SûÈo 3 elementos. Portanto teremos 2ô° subconjuntos de B, ou seja, a partir do conjunto B podem ser formados 8 subconjuntos. Nû°s jûÀ conhecemos, devido as propriedades da inclusûÈo, 2 destes subconjuntos: o conjunto vazio e o prû°prio conjunto B. Vamos combinar os elementos a, b e c de forma a encontrar os 6 demais subconjuntos de B.
Agora que jûÀ sabemos tudo sobre os subconjuntos e o conjunto das partes, podemos concluir este texto! Espero que vocûˆs tenham entendido direitinho todos os conceitos que estudamos. Em anexo, ûˋ claro, disponibilizo um vûÙdeo que complementa a abordagem desse texto, com outros exemplos resolvidos. Dar uma olhadinha nele sû° tem a contribuir para o conhecimento de vocûˆs!
Gostou deste conteû¤do?ô Clique aquiô para saber como aô Plataforma do Professor Ferrettoô funciona!
Deseja ter uma preparaûÏûÈo completa em matemûÀtica e ciûˆncias da natureza? EntûÈo conheûÏa os planos e cursos daô Plataforma do Professor Ferretto.ô Clique aquiô e vem com a gente garantir a sua vaga no ensino superior!
Fica aqui o meu abraûÏo e meu desejo de que vocûˆs tenham muito sucesso nos estudos! Atûˋ mais!
