A regra de três composta é uma maneira de relacionar mais de duas grandezas diretamente ou inversamente proporcionais. Isso significa que através da regra de 3 composta, é possível encontrar um valor desconhecido dentre n valores conhecidos em um contexto.

 

Olá, pessoal! Tudo bem com vocês?

A Regra de Três Simples, que nós já estudamos aqui no blog, nos permite resolver problemas que envolvem apenas duas grandezas. Contudo, existem algumas situações em que é necessário relacionar 3, 4, 5 ou mais grandezas, e infelizmente, elas gostam muito de aparecer no ENEM, nos vestibulares e inclusive na maioria dos concursos públicos.

Por isso, estamos aqui hoje para estudar a regra de três composta! Apesar de se tratar de matemática básica, essa operação costuma gerar uma série de dúvidas, não é? Se vocês não conhecem o assunto, ou pensam que é impossível entendê-lo, venham comigo! Nós vamos desvendar juntos todos os segredos desse cálculo logo mais!

Beleza, pessoal!? Sendo assim, chega de papo! Vamos iniciar nossos estudos!

 

1. COMO RESOLVER UMA REGRA DE TRÊS COMPOSTA?

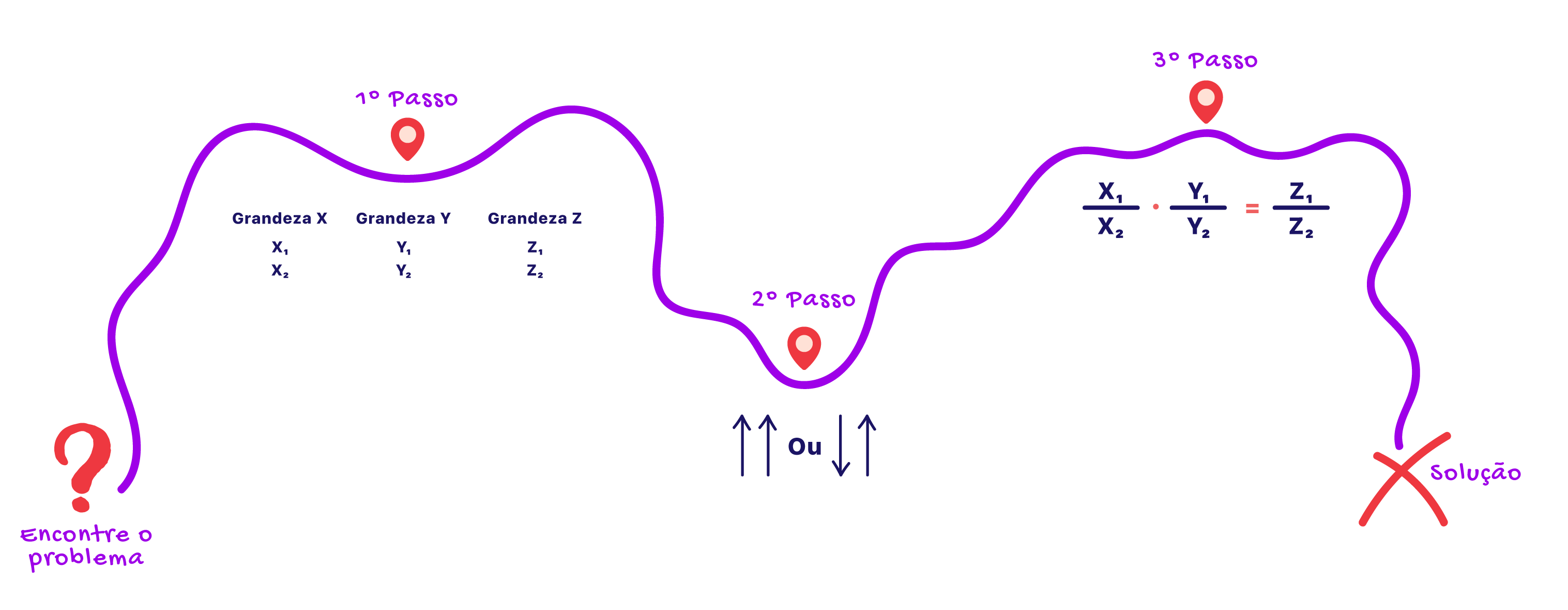
Quem já sabe como resolver uma regra de três simples pode ter certeza que conhece boa parte do processo que envolve a resolução de uma regra de 3 composta. Vejam através do mapa, que apenas três passos separam um problema que envolve a regra de três composta de sua solução. Vamos estudar cada um deles com detalhes através de um exemplo. Vem comigo!

José e Pedro decidiram fazer uma viagem de férias para o litoral brasileiro. José, que já havia feito este percurso, afirmou que rodando uma média de 8 horas por dia a uma velocidade média de 60 km/h, tinha levado 6 dias para completá-lo. Pedro comprometeu-se a dirigir 9 horas por dia a velocidade média de 80km/h.

Considerando que Pedro vá dirigindo, a quantidade de dias, que levarão para completar o percurso da viagem, será de:

a) 5 dias e meio
b) 6 dias
c) 4 dias e meio
d) 4 dias
e) 5 dias

 

1º PASSO: Separar em colunas as grandezas de mesmo tipo

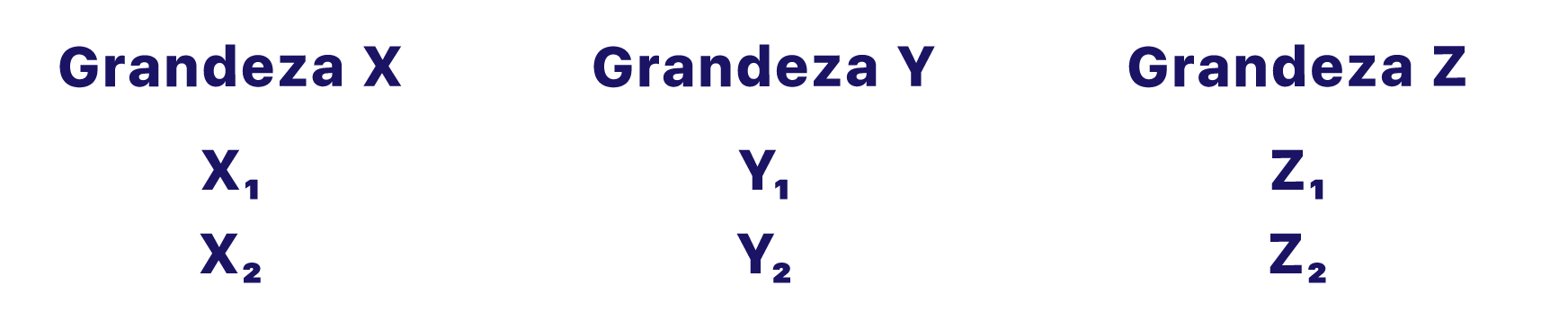
O primeiro passo rumo a resolução de uma regra de três composta é identificar e separar os valores de cada grandeza envolvida no problema em colunas diferentes. Portanto, o jeito é relermos o enunciado do exercício apresentado acima e identificarmos as grandezas envolvidas.

Reparem que o contexto é de uma viagem, e que os aspectos analisados para realizá-la são: o tempo (em horas) gasto por dia, a velocidade média utilizada (em km/h) e o número de dias necessários para chegar até o destino. Tempo, velocidade e dias são coisas que podemos contar ou medir. Por isso, essas são as grandezas do problema.

A questão nos pergunta o número de dias necessários para completar a viagem caso Pedro for dirigindo. Por isso, o valor que estamos procurando, ou seja, a incógnita x, deve estar na coluna dos dias. Vejam que nós escrevemos essa coluna bem a direita das demais. Não que seja extremamente necessário, mas procurem deixar a coluna que envolve a incógnita mais a direita ou a esquerda. Isso facilitará os passos que seguiremos logo mais.

 

Não deixem de verificar!

Da mesma forma que na regra de 3 simples, é muito importante ficarmos atentos a dois detalhes nesta etapa. O primeiro deles é que não podemos, de maneira alguma, misturar as grandezas envolvidas. Por isso, no nosso exercício deixamos os dois valores que se referem as horas gastas na viagem por dia na primeira coluna, os valores que se referem a velocidade na coluna central e aqueles que se referem aos dias à direita, sempre um embaixo do outro.

O outro detalhe importante é permitir que os valores que se correspondem estejam lado a lado. No nosso exercício, é dito que José afirmou que rodando uma média de 8 horas por dia a uma velocidade média de 60 km/h, tinha levado 6 dias para completar o percurso. Por esse motivo, deixamos os valores 8, 60 e 6 na mesma linha.

Entendido? Então sigam comigo rumo ao próximo passo!

 

2º PASSO: Identificar quais grandezas são diretamente ou inversamente proporcionais em relação a grandeza da incógnita

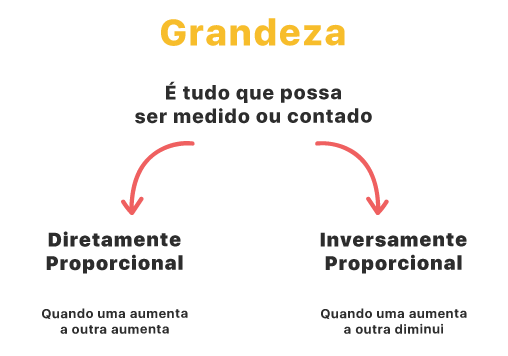
Nós falamos brevemente sobre o significado de grandeza no passo anterior, lembram? Uma grandeza costuma ser definida como algo que pode ser medido, contado, é uma quantidade de algo. Agora, vocês estão cientes da relação entre grandezas diretamente ou inversamente proporcionais? A imagem abaixo mostra o que acontece em cada uma delas.

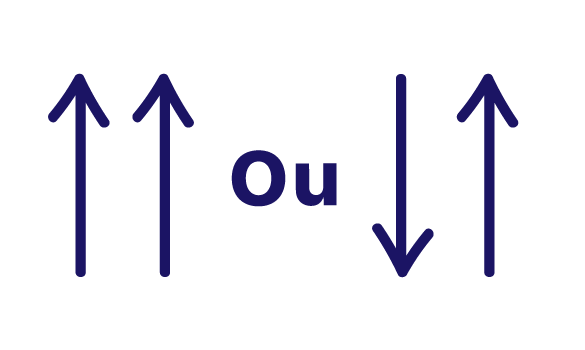
Entenderam a ideia? Pensando nesses conceitos, nós faremos uma comparação entre a grandeza da incógnita e as demais grandezas do exercício. Algumas setas irão nos ajudar nessa tarefa, acompanhem!

Comecem sempre inserindo uma seta apontando para cima ou para baixo na coluna da incógnita. O sentido que vocês adotarem nessa coluna é indiferente, porque a ideia é somente tomá-la como base para atribuir um sentido para as demais colunas, certo?

Neste momento, é hora de analisarmos se as grandezas horas/dia e velocidade são diretamente ou inversamente proporcionais a grandeza dias. Se alguma delas for diretamente proporcional a grandeza da incógnita, colocaremos uma seta em sua coluna apontando para o mesmo sentido que foi adotado na coluna da incógnita. Já se alguma delas for inversamente proporcional a grandeza de x, colocaremos uma seta em sua coluna no sentido contrário ao da coluna da incógnita.

A análise das grandezas diretamente ou inversamente proporcionais pode ser a parte mais complicada da resolução de uma regra de três composta. Isso porque ela sempre depende do contexto do exercício, e, portanto, da nossa interpretação sobre o caso. Vejam só como será o raciocínio utilizado para compararmos as grandezas do exercício.

 

Como definir a proporcionalidade entre as grandezas

Vamos começar confrontando as grandezas número de dias gastos na viagem, e número de horas por dia de viagem. Aí é só pensar no seguinte:

Se nós viajarmos mais horas por dia durante um longo percurso, certamente vamos chegar mais rápido do que se viajarmos poucas horas por dia. Assim, podemos concluir que se aumentarmos o número de horas de viagem por dia, vamos diminuir o número de dias necessários para completá-la. Isso significa que, nesse caso, horas por dia e dias são inversamente proporcionais. Desta maneira, precisaremos inserir uma seta no sentido contrário ao que adotamos para a coluna da incógnita, e, portanto, neste caso, a seta da coluna das horas por dia apontará para baixo.

Agora, vamos verificar a proporcionalidade entre a velocidade média do percurso, e o número de dias gastos na viagem. Novamente, reflitam no seguinte sentido:

Se aumentarmos a velocidade durante uma viagem, nós vamos diminuir o tempo de percurso, porque vamos percorrer uma distância maior a cada período de tempo. Percorrendo uma distância maior, nós chegaremos mais rápido, portanto, demoraremos menos dias para completar a viagem. Por isso, as grandezas velocidade e dias, nesse caso, também são inversamente proporcionais. Assim, vamos inserir uma seta para baixo na coluna da velocidade, ou seja, uma seta no sentido contrário ao da grandeza dias.

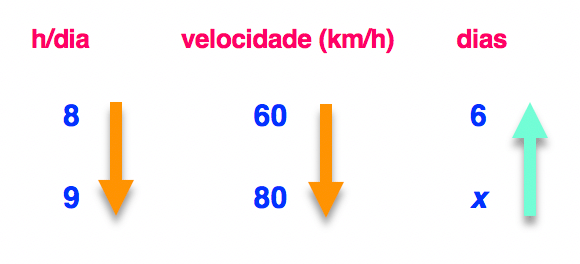
Ficou claro, pessoal? Acreditem, 80% do problema já foi resolvido! Vamos ao último passo da operação!

 

3º PASSO: Montar a proporção e resolver a equação

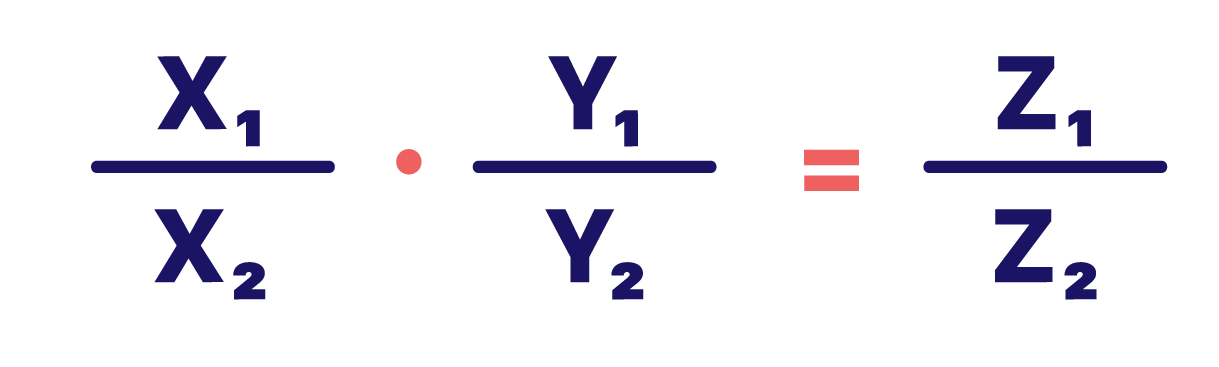
O terceiro e último passo para resolvermos uma regra de três composta consiste basicamente em montarmos uma equação. Essa equação será construída através da combinação entre as razões formadas por cada coluna que criamos. De um lado da igualdade, colocaremos a razão formada pela coluna em que a incógnita se localiza, exatamente como ela se encontra na coluna. Por sua vez, do outro lado, faremos o produto das razões das demais colunas, tomando o seguinte cuidado: se a grandeza for diretamente proporcional a grandeza da incógnita, basta montarmos uma razão igualzinha a da coluna que havíamos construído. Contudo, se a grandeza for inversamente proporcional a da incógnita, inverteremos os termos de lugar em relação a como eles eram localizados na coluna.

Um tanto confuso, não é? Mas aplicando a ideia no nosso exercício, vai ficar mais fácil, acreditem!

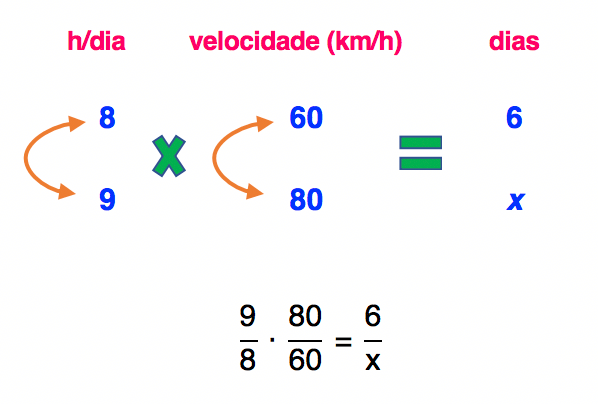
A partir daí é só uma questão de manipulação algébrica. Podemos seguir o cálculo sem realizar simplificação alguma, mas também dá para realizar uma série simplificações e facilitar o trabalho. Independente da maneira escolhida, chegaremos ao mesmo resultado, olhem só!

 

Finalizando com chave de ouro! 

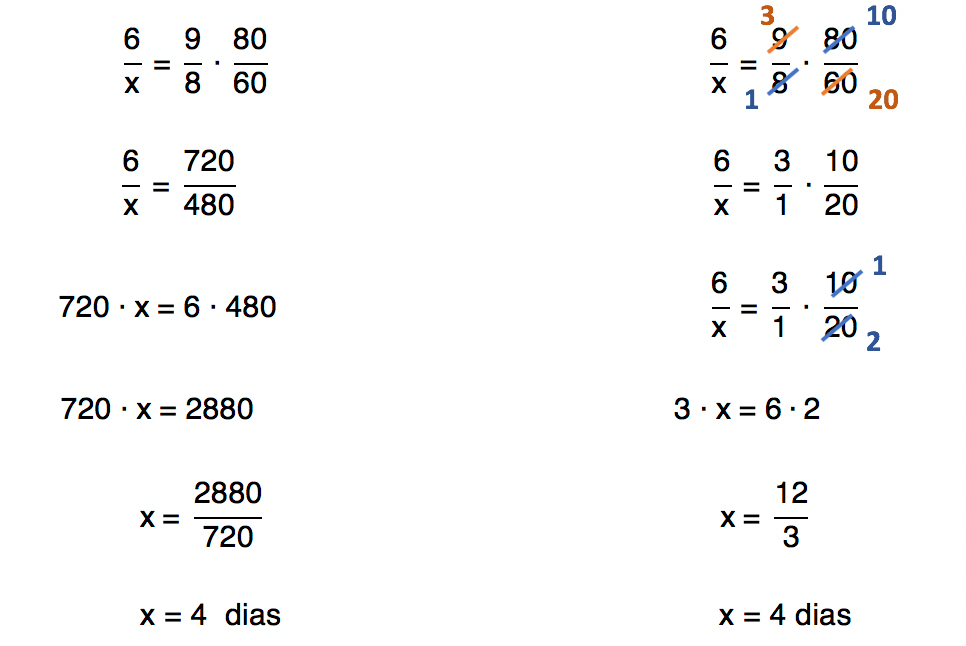
Tranquilo, não é, pessoal? Como foi mencionado, talvez o mais difícil seja identificar quais grandezas são diretamente ou inversamente proporcionais a grandeza da incógnita. Mas aí é só manter a calma! Tudo isso se resolve com muito treino e dedicação.

E aí, que tal resolver mais alguns exercícios comigo? No vídeo que deixei em anexo, vocês encontram mais algumas questões sobre a regra de 3 composta, inclusive, com mais de 3 grandezas envolvidas. Espero vocês por lá!

Gostou deste conteúdo? Clique aqui para saber como a Plataforma do Professor Ferretto funciona!

Deseja ter uma preparação completa em matemática e ciências da natureza? Então conheça os planos e cursos da Plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!

Um abração, muito sucesso e até breve!