
Os assuntos de biologia que mais caem no Enem são uma das preocupaçÔes de quem estå se preparando para a...

Quer saber tudo sobre a propriedade que envolve o quadrilĂĄtero inscrito na circunferĂȘncia? EntĂŁo, vem comigo aqui, e desvende este mistĂ©rio!
Podemos dizer que um quadrilĂĄtero estĂĄ inscrito em uma circunferĂȘncia, quando todos os 4 vĂ©rtices desse polĂgono de 4 lados tocam o seu segmento. Pode nĂŁo parecer, mas esse fenĂŽmeno matemĂĄtico dĂĄ origem a uma propriedade muito interessante, que torna este texto imperdĂvel!
OlĂĄ, pessoal! Tudo bem com vocĂȘs?
Estamos aqui novamente para estudar mais um belĂssimo conceito que a geometria plana nos traz. Ă verdade que diversas figuras geomĂ©tricas podem se inscrever na circunferĂȘncia, mas quando isso ocorre com o quadrilĂĄtero, os seus Ăąngulos internos se comportam de uma maneira muito interessante. Querem descobrir que maneira Ă© essa? EntĂŁo, sigam comigo!
Vamos começar? Mal posso esperar para mostrar para vocĂȘs como entender e aplicar o conceito de quadrilĂĄtero inscrito na circunferĂȘncia.
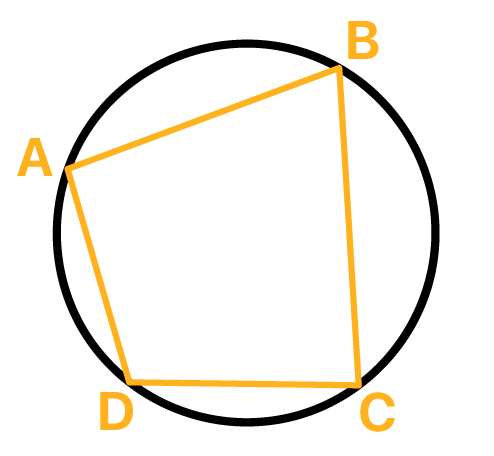
Se um quadrilĂĄtero estĂĄ inscrito em uma circunferĂȘncia, entĂŁo os seus Ăąngulos opostos sĂŁo suplementares.
Dois Ăąngulos sĂŁo suplementares, quando juntos somam 180Âș. Assim, podemos concluir que no caso apresentado na imagem acima, os Ăąngulos dos vĂ©rtices A e C, e B e D sĂŁo suplementares.
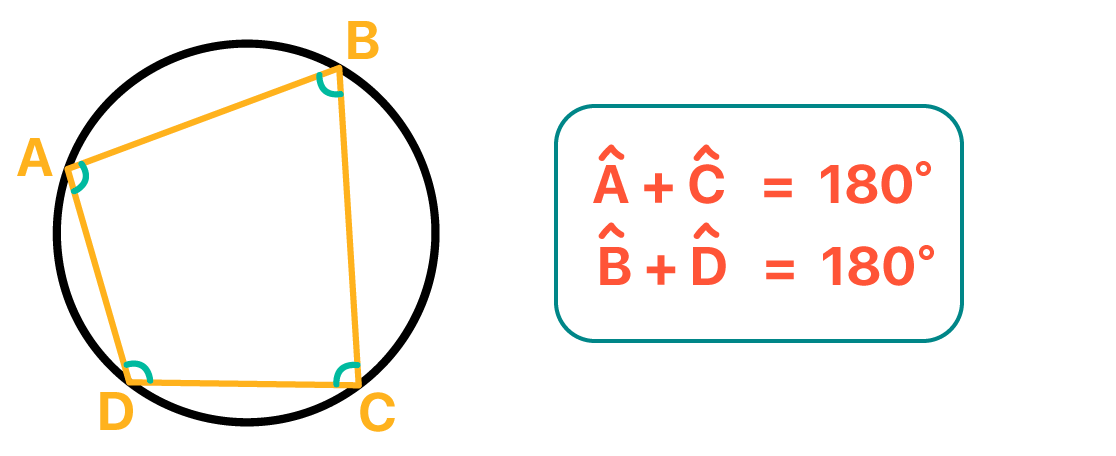
E nĂŁo Ă© que as duas somas dos Ăąngulos opostos do quadrilĂĄtero inscrito na circunferĂȘncia resultam em 180Ë? EntĂŁo Ă© vĂĄlido afirmarmos que uma soma Ă© igual a outra, nĂŁo Ă© mesmo? Isso nos leva a seguinte fĂłrmula:
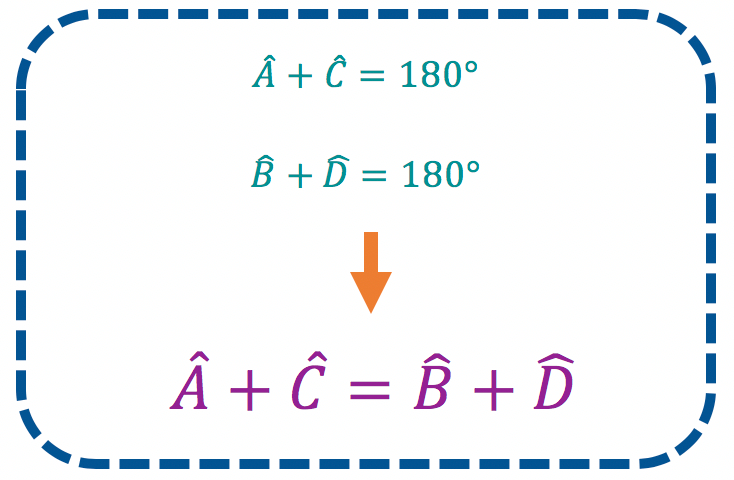
TambĂ©m podemos visualizar este contexto de um segundo ponto de vista. Para que um quadrilĂĄtero possa ser inscrito a uma circunferĂȘncia, os seus Ăąngulos opostos devem, necessariamente, ser suplementares. De outra forma, ou seja, sem atender a essa condição, nĂŁo haveria como inscrever um polĂgono de 4 lados em uma circunferĂȘncia.
Feito, pessoal? Depois de analisarmos essa propriedade, nada Ă© melhor do que partirmos logo para um exercĂcio. AtravĂ©s deste exemplo, nĂłs vamos consolidar o conhecimento quanto ao quadrilĂĄtero inscrito, e de quebra, revisaremos outros conceitos relacionados aos Ăąngulos na circunferĂȘncia. Vem comigo!
Determine o valor de x na figura abaixo, sabendo-se que o arco AB mede 100Âș.
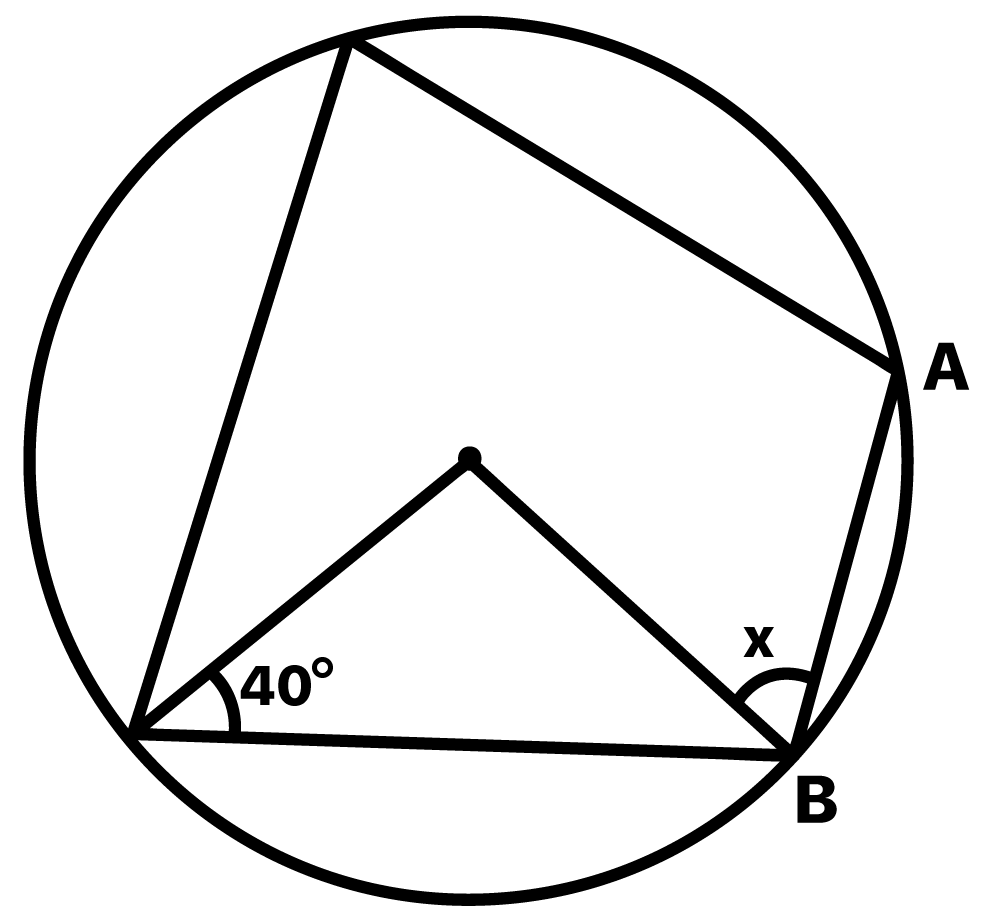
Humm, parece que nesse caso temos a presença duas figuras geomĂ©tricas conhecidas dentro da circunferĂȘncia. Uma delas Ă© o nosso quadrilĂĄtero, claro, e a outra um triĂąngulo! Bom, o jeito Ă© começar pela informação que nos foi dada no enunciado: o arco AB mede 100Âș.
Segundo o que vimos no texto Elementos da circunferĂȘncia e do cĂrculo, um arco é a porção compreendida entre quaisquer dois pontos de uma circunferĂȘncia. Isso significa que o arco AB, Ă© a porção da circunferĂȘncia compreendida entre os pontos A e B.
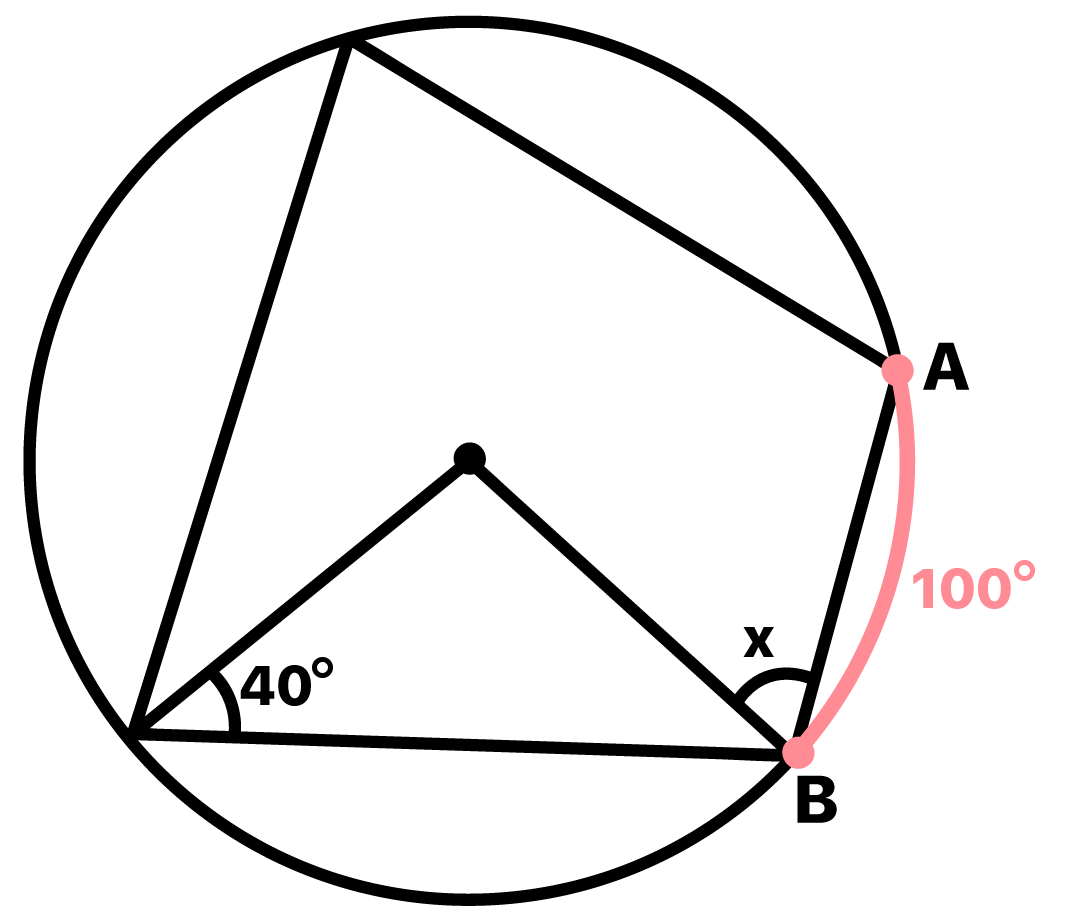
Agora, convido vocĂȘs a repararem com atenção neste triĂąngulo presente na figura. Um de seus lados Ă© coincidente com um dos lados do quadrilĂĄtero inscrito, enquanto os outros dois se unem exatamente no centro da circunferĂȘncia, cujo ponto nĂłs denominaremos O. Ora, se esses dois lados sĂŁo segmentos que saem do centro da circunferĂȘncia, e vĂŁo atĂ© a sua borda, significa que ambos possuem comprimento equivalente ao raio da circunferĂȘncia. E se um triĂąngulo tem dois lados iguais, ele sĂł pode ser um triĂąngulo isĂłsceles!
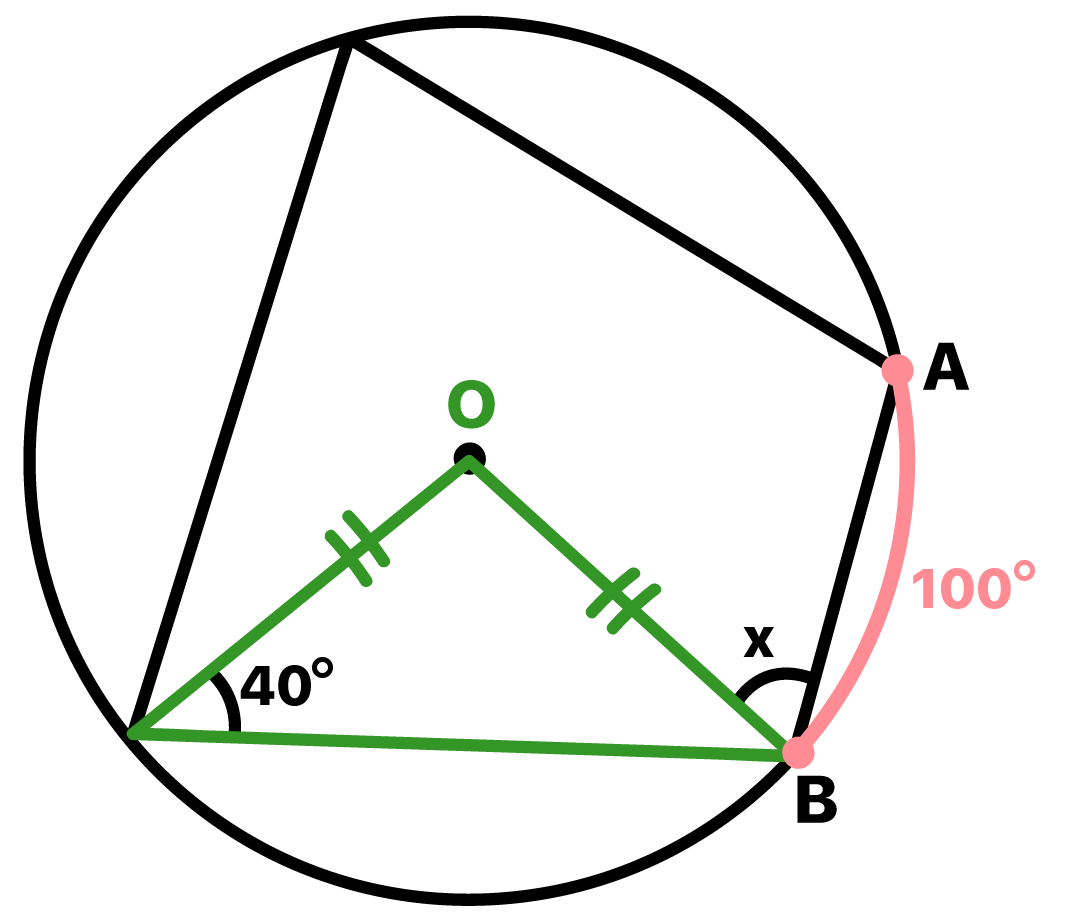
Um triùngulo isósceles não possui somente dois lados iguais, como também possui dois ùngulos iguais! Isso nos leva a encontrar mais um ùngulo do sistema, como mostra a imagem seguinte.
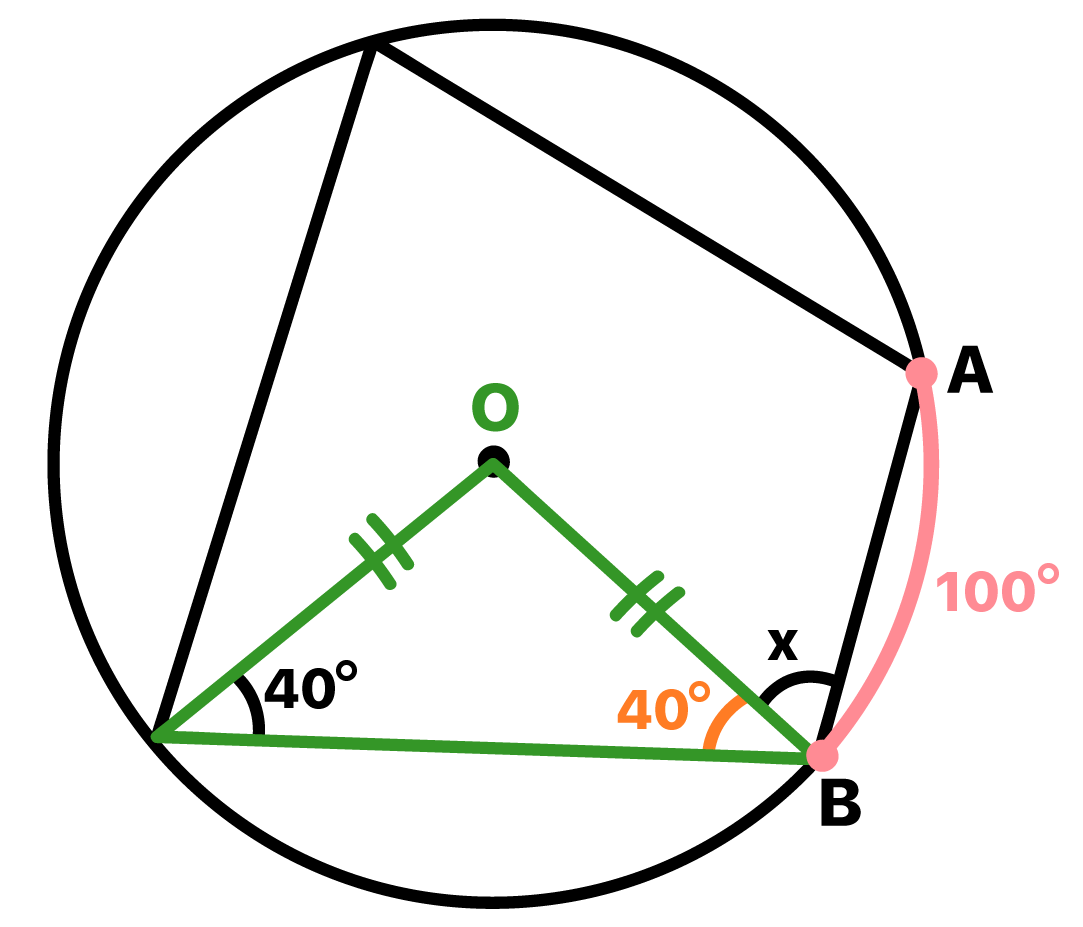
Levando em conta a famosa propriedade que diz que a soma dos Ăąngulos internos de qualquer triĂąngulo Ă© sempre 180Âș, podemos encontrar o valor do Ăąngulo Ă:
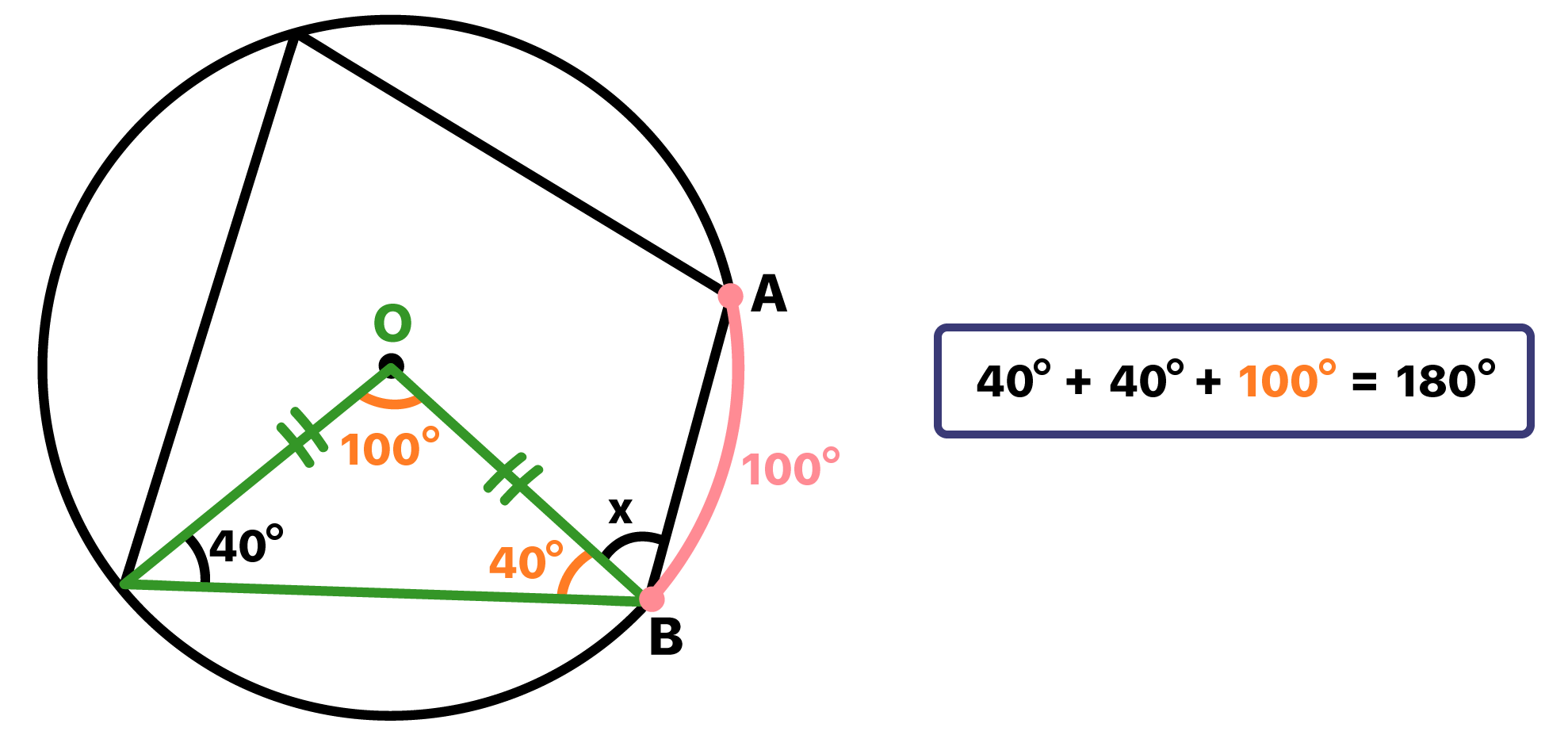

Calma, pessoal! Antes de entendermos como o quadrilĂĄtero inscrito na circunferĂȘncia vai contribuir para o desenrolar dessa questĂŁo, precisamos relembrar dois conceitos muito importantes jĂĄ vistos aqui no blog. Um deles Ă© o de Ăąngulo central a circunferĂȘncia. Segundo o texto que aborda o assunto, um Ăąngulo central é aquele cujo vĂ©rtice se localiza exatamente no centro da circunferĂȘncia.
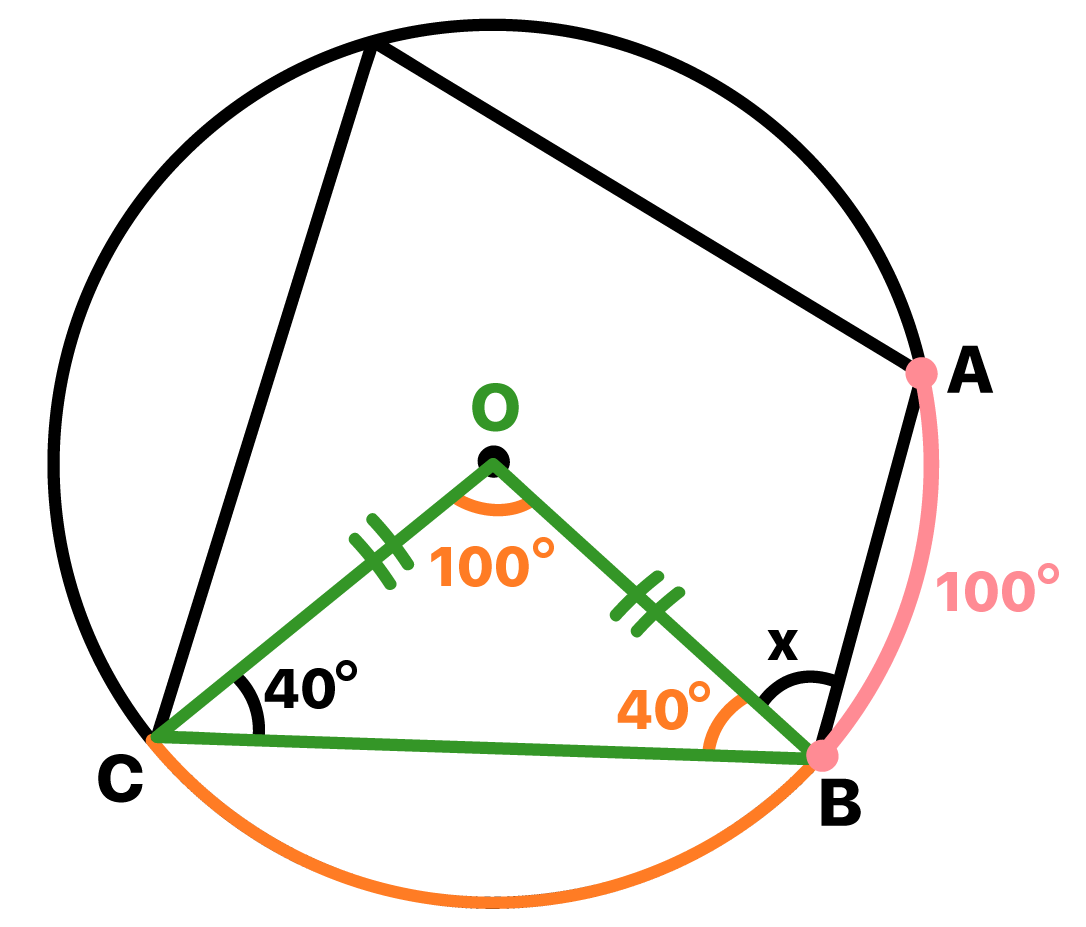
E nĂŁo Ă© que o Ăąngulo Ă pode ser visto como um Ăąngulo central? Pois bem, o arco correspondente a esse Ăąngulo, Ă© justamente aquele que inicia no ponto B, e vai atĂ© o ponto C, que nomeamos na imagem acima. Mas o melhor de tudo ainda estĂĄ por vir: segundo o texto Ăngulo central e Ăąngulo inscrito na circunferĂȘncia, a medida de um arco de circunferĂȘncia Ă© igual Ă medida do Ăąngulo central correspondente.
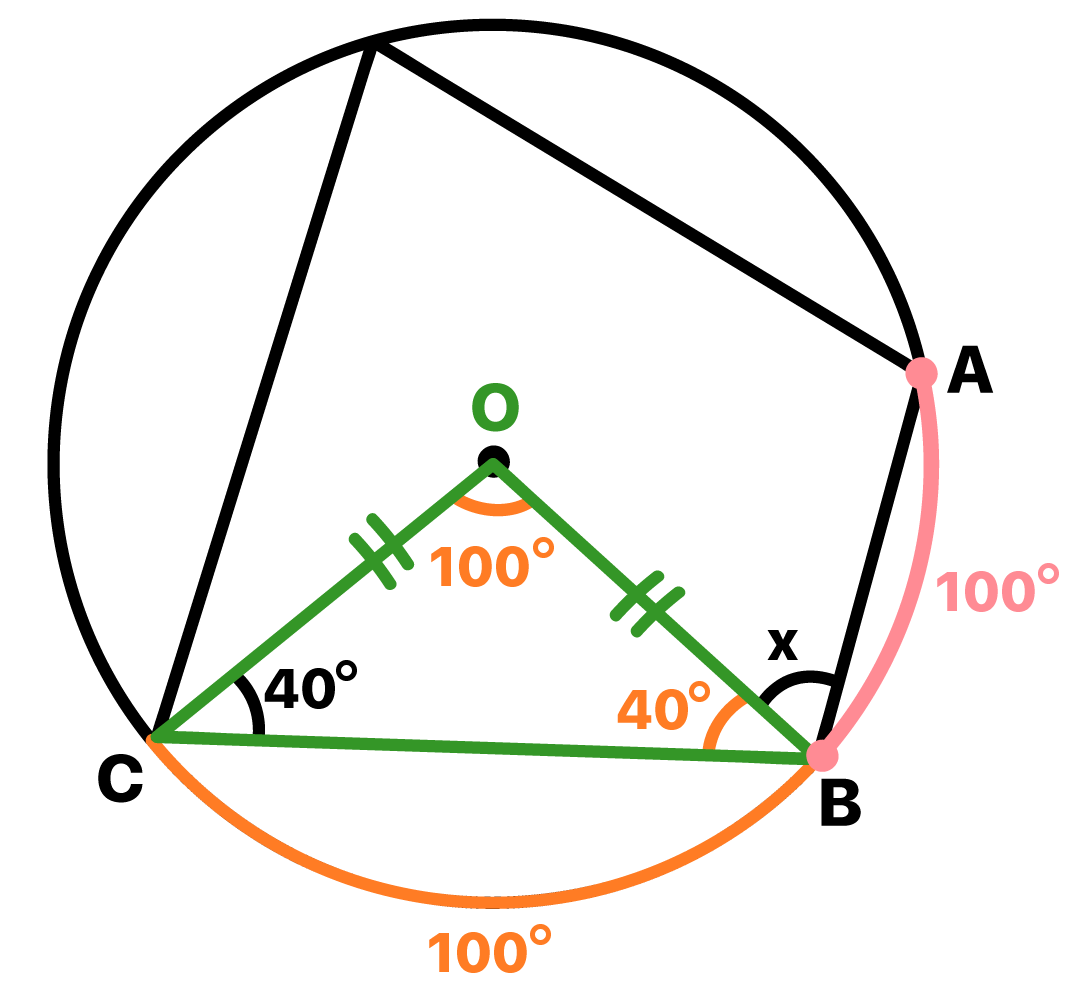
E aĂ, tudo certo atĂ© aqui, pessoal? Fiquem tranquilos, estamos quase lĂĄ! Lembram que eu falei de dois conceitos importantes que precisĂĄvamos lembrar? Pois entĂŁo, um deles era o Ăąngulo central, e o outro Ă© o Ăąngulo inscrito na circunferĂȘncia.Â
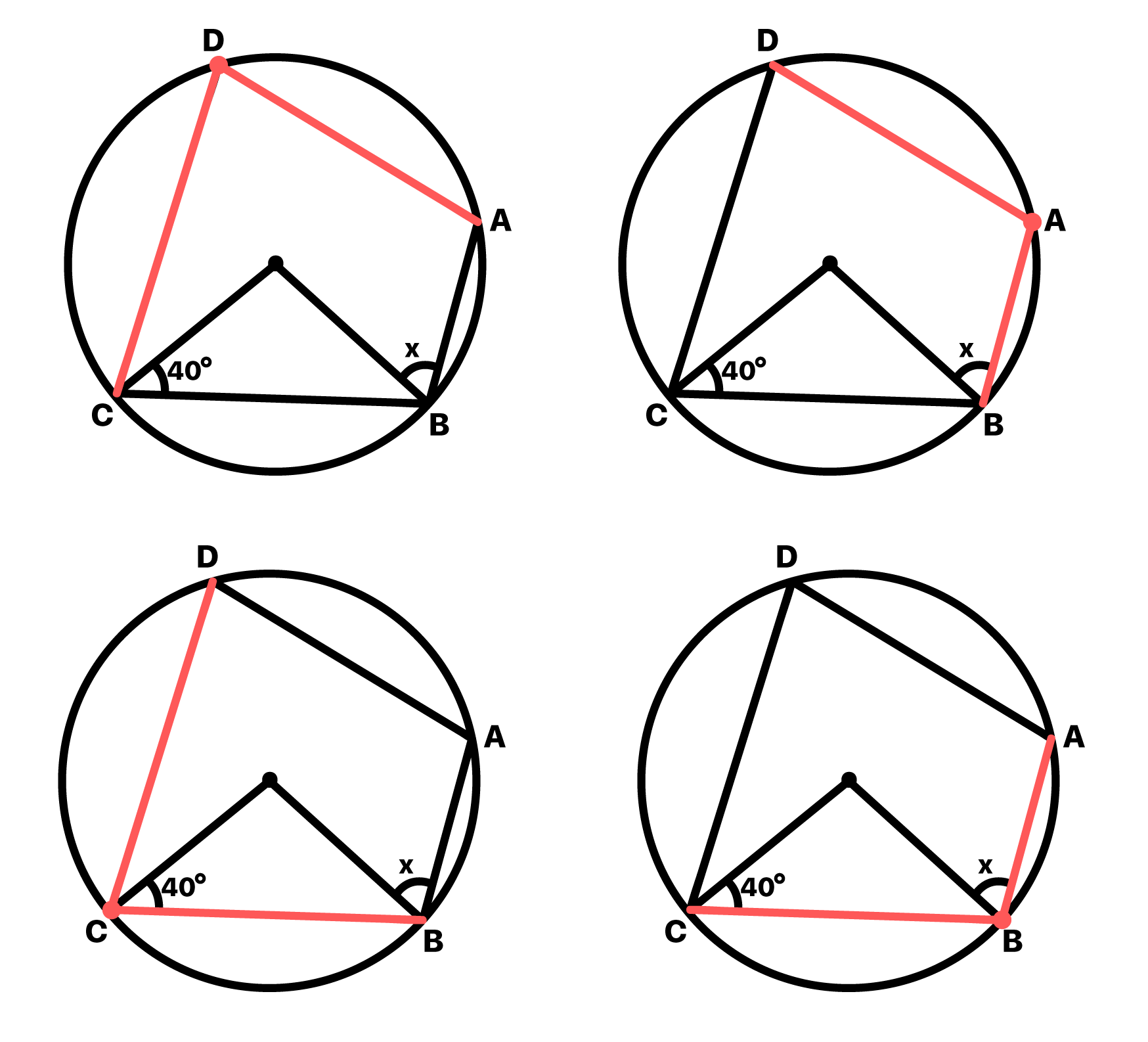
O Ăąngulo inscrito é aquele cujo vĂ©rtice se localiza na circunferĂȘncia e cujos lados sĂŁo secantes a ela. Tendo esse conceito em vista, podemos perceber que cada vĂ©rtice do quadrilĂĄtero inscrito na circunferĂȘncia Ă© na verdade o vĂ©rtice de um Ăąngulo inscrito. E agora, alguĂ©m aĂ arrisca o que isso tem a ver com tudo que havĂamos analisado anteriormente?
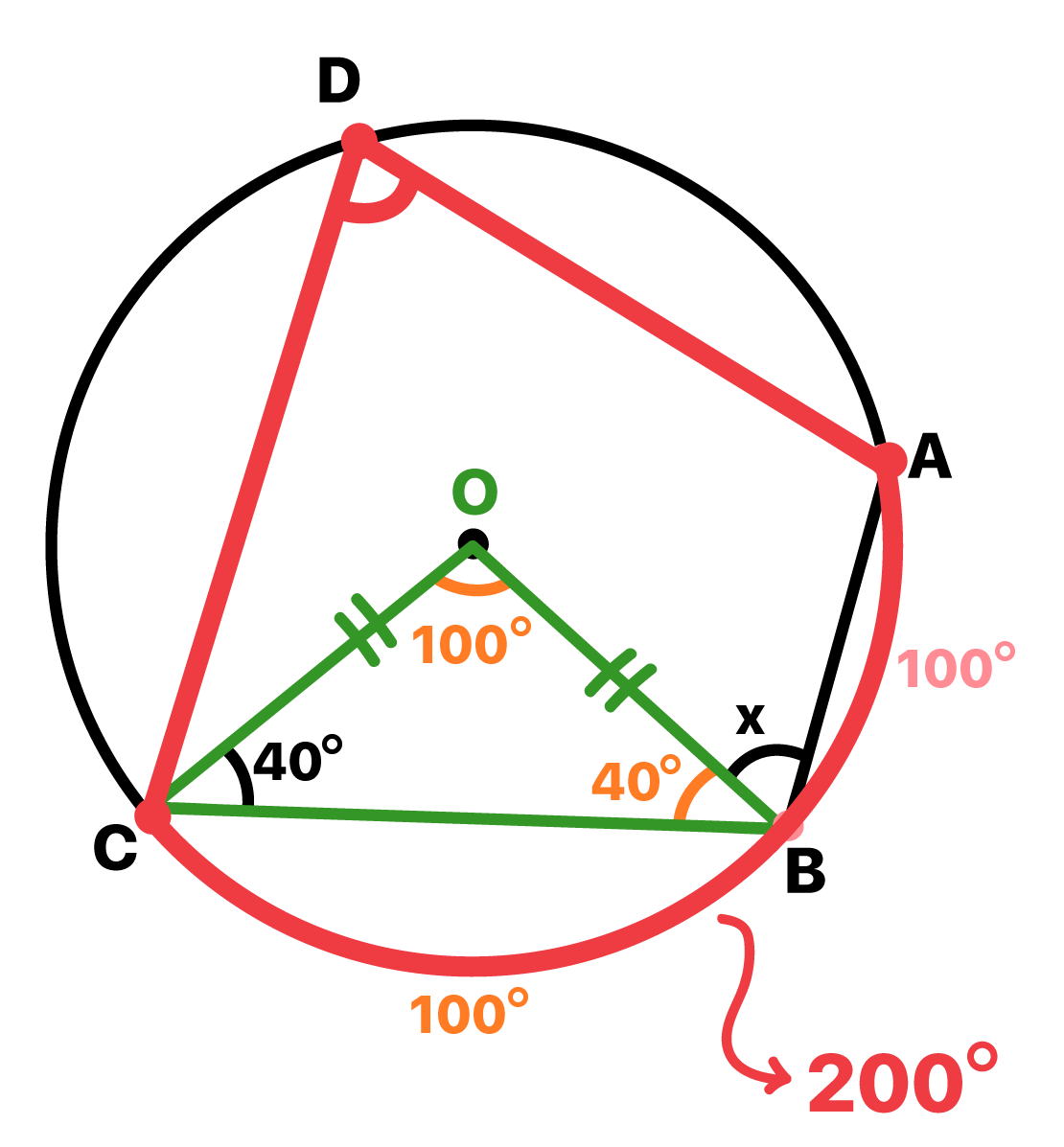
Pois bem, o Ăąngulo inscrito cujo vĂ©rtice Ă© o ponto que chamamos de D, possui um arco correspondente cujo valor conhecemos, 200Âș. Esse arco Ă© equivalente a soma dos arcos AB e BC! E nĂŁo Ă© que o texto Ăngulo central e Ăąngulo inscrito a circunferĂȘncia vai nos ajudar novamente? Claro, segundo este texto, o Ăąngulo inscrito Ă© equivalente a metade da medida do seu arco correspondente, em termos de Ăąngulo.
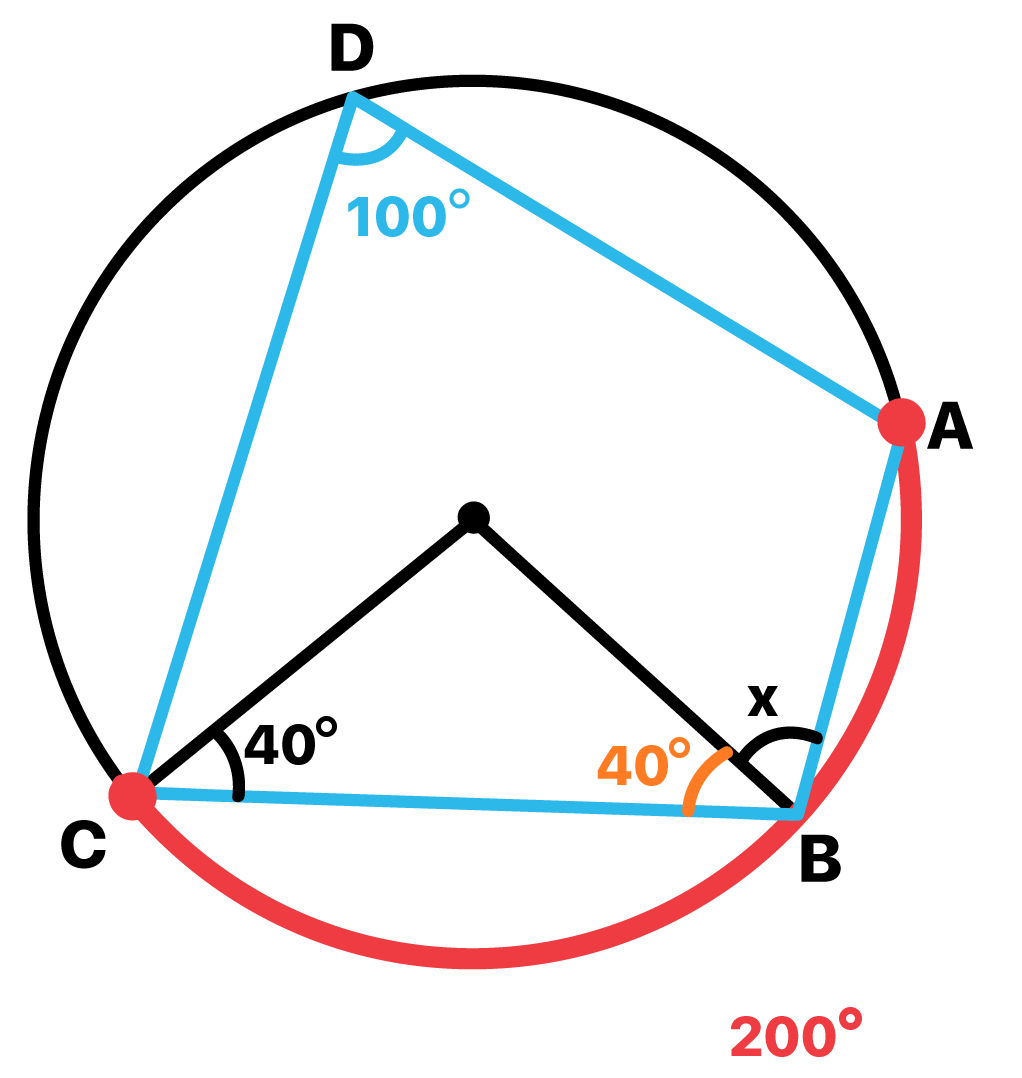
Assim, podemos concluir que o Ăąngulo do vĂ©rtice D Ă© igual a 100Âș, a metade de 200Âș. Essa informação Ă© de extrema importĂąncia para nĂłs, jĂĄ que dessa forma, temos o conhecimento de dois Ăąngulos do quadrilĂĄtero inscrito: o do vĂ©rtice D, 100Âș, e o do vĂ©rtice B, 40Âș + x. E se eu disser para vocĂȘs que esses dois Ăąngulos sĂŁo opostos, e portanto, suplementares? Sim, finalmente chegou o momento de aplicarmos a propriedade do quadrilĂĄtero inscrito na circunferĂȘncia!
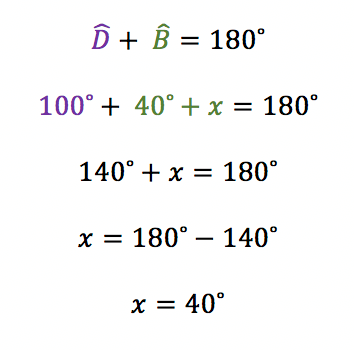
Ufa, essa nĂŁo foi fĂĄcil! Ă que a geometria plana gosta mesmo de envolver vĂĄrios conceitos dentro de um Ășnico exercĂcio. Mas nĂŁo tem problema, nĂłs vamos aprender tudo o que envolve os Ăąngulos na circunferĂȘncia aqui no blog! NĂŁo deixem de acompanhar todos os posts e de revisar o conteĂșdo atravĂ©s do vĂdeo que deixo aqui embaixo. Vamos juntos acabar com as dĂșvidas em matemĂĄtica!
Gostou deste conteĂșdo? Clique aqui para saber como a Plataforma do Professor Ferretto funciona!
Deseja ter uma preparação completa em matemĂĄtica e ciĂȘncias da natureza? EntĂŁo conheça os planos e cursos da Plataforma do Professor Ferretto. Clique aqui e vem com a gente garantir a sua vaga no ensino superior!
Espero que vocĂȘs tenham gostado deste texto, pessoal! Sucesso nos estudos aĂ e atĂ© o prĂłximo post!
