INTERVALOS REAIS

Olá pessoal, tudo certo?

Hoje nós estudaremos um assunto muito importante dentro dos conjuntos numéricos: os intervalos reais! Vocês sabem como representar um intervalo aberto, fechado, ou infinito? Não? Então vieram ao lugar certo! Acompanhem o texto com atenção, porque todos esses temas que serão tratados aqui também são base para outros conteúdos da matemática do ensino médio, aqueles que podem cair nas temidas provas do ENEM e dos vestibulares!

E se vocês pretendem prestar essas provas, mas não estão conseguindo organizar seus estudos ou mesmo encontrar um material de qualidade, então eu indico mais um lugar interessante: a plataforma do Professor Ferretto! Só lá vocês encontram todo o conteúdo da matemática do ensino médio e de física também! Física?! Pois é, o curso do Professor Ferretto disponibiliza esse bônus a todos os alunos assinantes. Seja um aluno do Professor Ferretto! Acesse o site e saiba como é fácil assinar a plataforma! 

Feito, pessoal? Então vamos começar, ou ficaremos falando das vantagens da plataforma do Ferretto por horas!

É fato que os intervalos reais podem ser definidos da seguinte maneira:

Os intervalos são subconjuntos de ℝ determinados por desigualdades.

Um conjunto é subconjunto de outro, quando todos os seus elementos também fazem parte deste outro conjunto. Ora, se o conjunto de quem estamos falando é o dos números reais (ℝ), então qualquer trecho de valores que escolhermos dentro da reta real, pode formar um subconjunto dos números reais, ou seja, um intervalo.

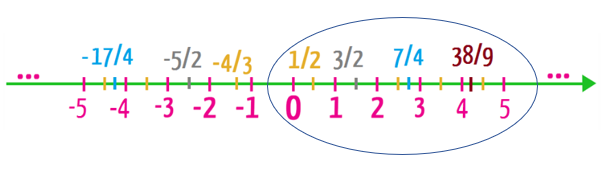
Observando a região destacada na reta real acima, poderíamos formar um subconjunto dos números reais, que começaria, por exemplo, no número zero e iria até o número 5, incluindo os próprios 0 e 5. Se esse subconjunto ou intervalo fosse chamado de A, ele poderia ser representado da seguinte maneira:

A = {x ∈ ℝ | 0 ≤ x ≤ 5}

E aí, vocês conseguiram reparar em alguns sinais conhecidos que determinam esse subconjunto? Pois então, para quem nunca viu, maior (>), menor (<), maior ou igual (≥) e menor ou igual (≤), são os chamados sinais de desigualdade. Aí é só pensar no seguinte: existe maneira melhor de definir um conjunto de valores do que afirmando que esses valores são maiores, menores, maiores ou iguais ou menores ou iguais a um ou dois valores de referência? Não, né? Por isso, diz-se que os intervalos são determinados por desigualdades!

E falando nos valores de referência, vejam que no intervalo do exemplo, os números 0 e 5 realmente faziam parte do intervalo, ou eram incluídos no subconjunto. Só que a verdade é que nem sempre isso acontece. Às vezes, os valores de referência servem apenas para delimitar o intervalo ou o conjunto de valores que realmente pertence ao subconjunto. É essa a diferença que define os conceitos de intervalo aberto e fechado que nós vamos estudar agora. Então, vem comigo aqui!

1. INTERVALO ABERTO

Um intervalo é aberto, quando os valores de referência a e b que o delimitam, não fazem parte do intervalo em si.

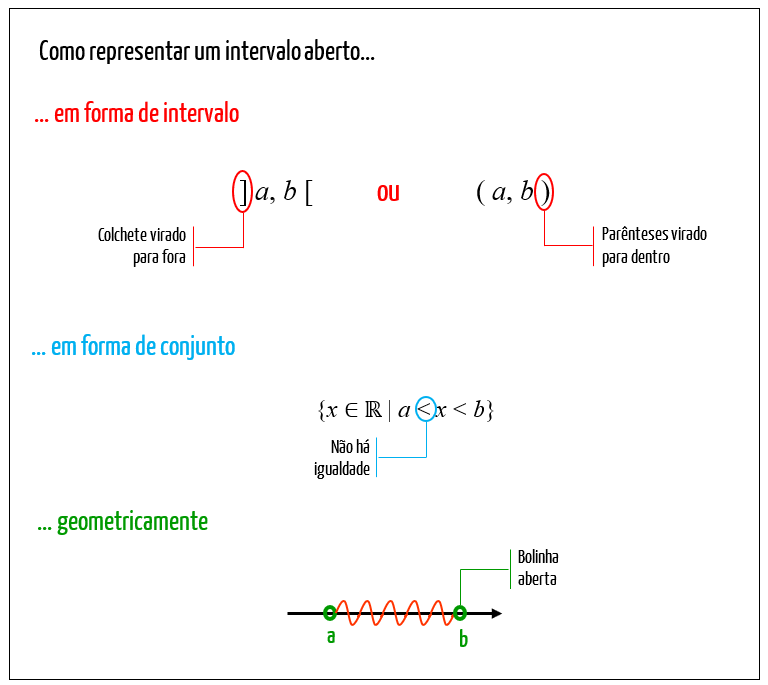
Quando valores numéricos são utilizados fica muito mais fácil, não é mesmo? Então, reparem no exemplo de intervalo aberto logo abaixo:

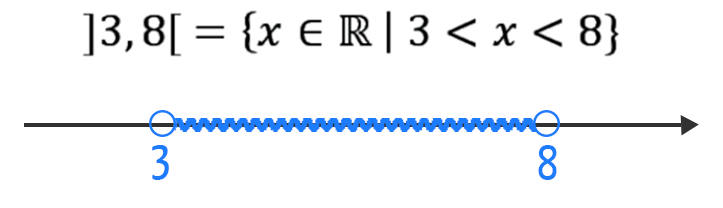
A partir de qualquer uma das 3 formas de representação deste intervalo, nós podemos dizer que qualquer valor real que esteja entre 3 e 8, seja ele racional ou irracional, faz parte do intervalo, sem incluir os próprios números 3 e 8.

2. INTERVALO FECHADO

Um intervalo é fechado, quando os valores de referência a e b que o delimitam, fazem parte do intervalo em si.

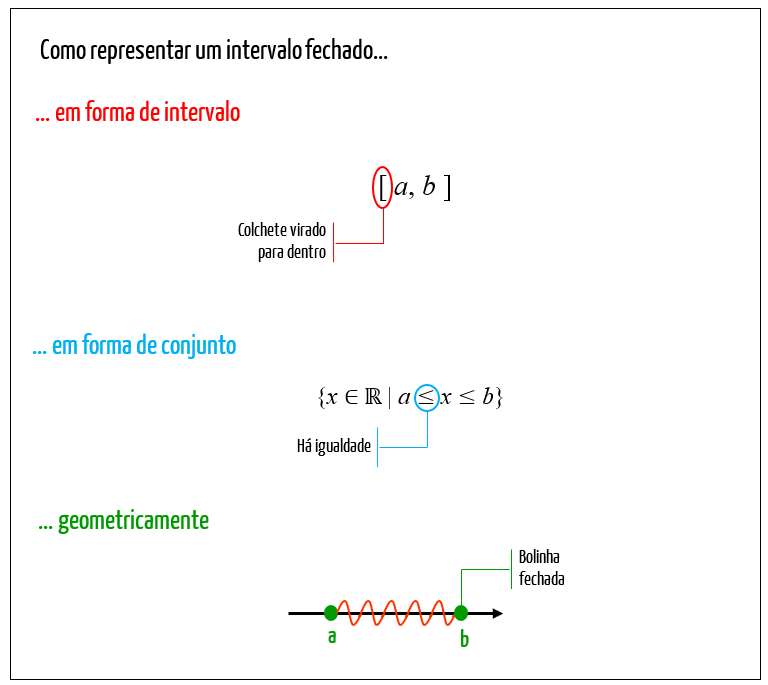
Reparem na representação em forma de intervalo deste caso: não parece que o colchete está abraçando os valores que delimitam o intervalo? Essa ideia pode ajudá-los a memorizar a diferença entre um intervalo aberto e um intervalo fechado. Agora vamos àquele famoso exemplo numérico!

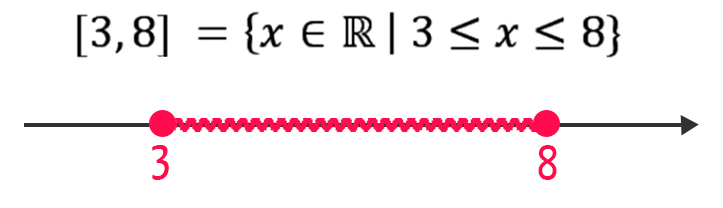
Observem que qualquer uma das representações do intervalo acima nos mostra que ele é composto por todos os valores reais que se situam entre 3 e 8, sejam eles racionais ou irracionais, incluindo os próprios números 3 e 8.

Mas o fato é que os intervalos não poderiam se restringir apenas a serem totalmente fechados ou totalmente abertos. Por isso, é possível que vocês se deparem com casos como esses:

• Intervalo fechado à esquerda e aberto à direita.

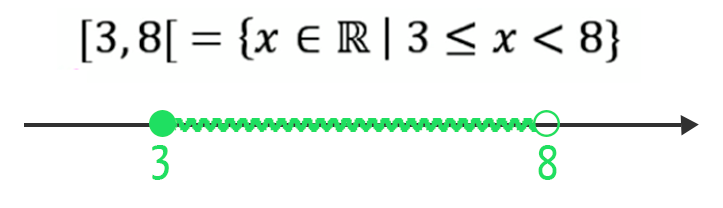
Neste caso, vejam, todos os valores reais que se situam entre 3 e 8, sejam eles racionais ou irracionais, fazem parte do intervalo, incluindo o número 3, já que ali o intervalo é fechado, mas excluindo o número 8, porque ali o intervalo é aberto.

• Intervalo aberto à esquerda e fechado à direita.

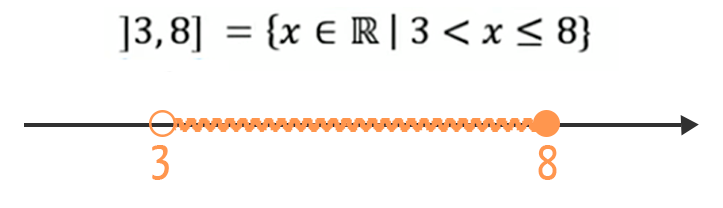
Agora as coisas mudam um pouco de figura. Fazem parte deste intervalo todos os números reais que se situam entre 3 e 8, sejam eles racionais ou irracionais, incluindo o número 8, já que ali o intervalo é fechado, mas excluindo o número 3, já que ali o intervalo é aberto.

Até aqui tudo tranquilo, não é pessoal? Mas e se vocês quisessem montar um intervalo que compreendesse todos os valores acima ou abaixo de um único valor de referência, será que seria possível? A resposta para essa pergunta se encontra no próximo item deste texto.

3. INTERVALO INFINITO

Algo que é infinito não tem fim, não termina, ou seja, não possui delimitações. Por isso, quando a ideia é obter um subconjunto dos números reais (ℝ), formado por todos os valores maiores, maiores ou iguais, menores, ou menores ou iguais a um único valor de referência, nós utilizamos os termos “mais infinito” (+∞) e “menos infinito” (-∞) como o segundo valor de referência na representação do intervalo.

Querem ver como funciona na prática? Então acompanhem comigo aqui!

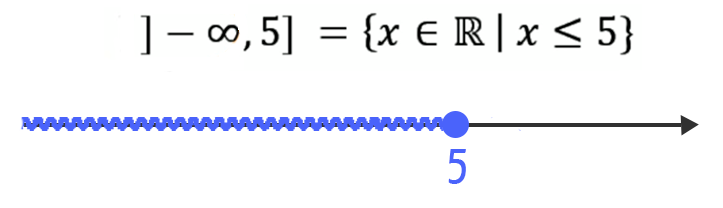
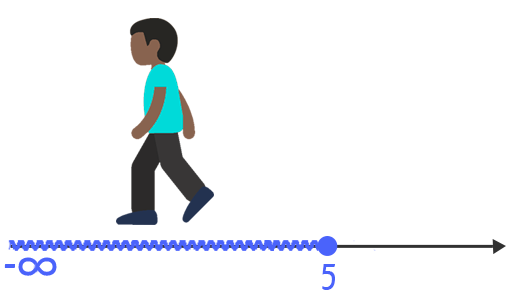
O intervalo acima é formado por todos os números reais menores ou iguais a 5. Isso significa que o próprio número 5 entra no intervalo, e que o valor de referência a sua esquerda é o “menos infinito”. Quando nos referimos aos valores à esquerda de um certo número, é como se estivéssemos nos deslocando rumo aos números negativos. Por isso, sempre que o objetivo for representar valores menores ou menores ou iguais a um valor de referência, é o menos infinito que entrará em cena.

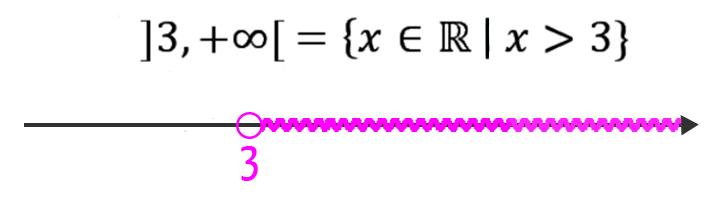
Já neste último intervalo, nós podemos observar uma diferença importante: ele é formado por todos os números reais maiores do que 3. Isso significa que o próprio número 3 não entra no intervalo, e que o valor de referência a sua direita é o “mais infinito”. Quando nos referimos aos valores a direita de um certo número, é como se estivéssemos nos deslocando rumo aos números positivos. Por isso, sempre que o objetivo for representar valores maiores ou maiores ou iguais a um valor de referência, deve-se usar o termo mais infinito.

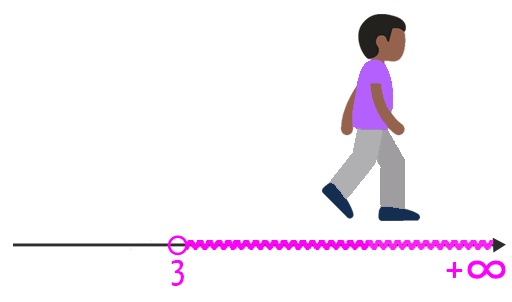
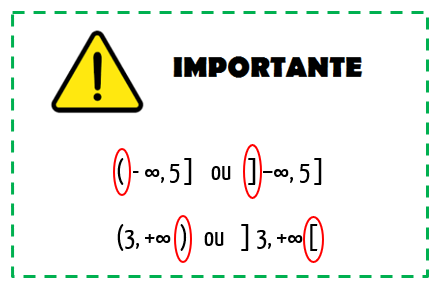
Pessoal, não sei se vocês repararam, mas quando tratamos de intervalos infinitos, seja à esquerda ou à direita, eles sempre formaram intervalos abertos! Por isso, fiquem extremamente atentos a esse detalhe: sempre que for representado um intervalo infinito, este deve ser aberto. Não importa se a representação utilizar os colchetes virados para fora, ou os parênteses, isso fica a critério de cada um. O importante mesmo é nunca representar um intervalo como esse sendo fechado!

Entendido? Porque chegou a hora de encerrarmos mais um texto! Espero que essa abordagem tenha facilitado o aprendizado de vocês no assunto, fazendo com que esse conhecimento possa ser utilizado sempre que precisarem! E olha que hoje não dá para perder o vídeo que está em anexo aqui embaixo. Nele, são abordados com mais detalhes alguns conceitos importantes, que complementam tudo que foi visto neste texto!

Um abraço a todos e até breve!